2.3E: Limit Laws and Techniques for Computing Limits EXERCISES

2.3: The Limit Laws

In the following exercises, use the limit laws to evaluate each limit. Justify each step by indicating the appropriate limit law(s).

83) lim𝑥→0⁡(4⁢𝑥2 −2⁢𝑥 +3)

Answer:

Use constant multiple law and difference law:

lim𝑥→0⁡(4⁢𝑥2 −2⁢𝑥 +3) =4⁢lim𝑥→0⁡𝑥2 −2⁢lim⁡𝑥→0⁢𝑥 +lim𝑥→0⁡3 =3

84) lim𝑥→1⁡𝑥3+3⁢𝑥2+54−7⁢𝑥

85) lim𝑥→−2⁡√𝑥2−6⁢𝑥+3

Answer:

Use root law: lim𝑥→−2⁡√𝑥2−6⁢𝑥+3 =√lim𝑥→−2⁡(𝑥⁢2−6⁢𝑥+3) =√19

86) lim𝑥→−1⁡(9⁢𝑥+1)2

In the following exercises, use direct substitution to evaluate each limit.

87) lim𝑥→7⁡𝑥2

Answer:

49

88) lim𝑥→−2⁡(4⁢𝑥2 −1)

89) lim𝑥→0⁡11+sin⁡𝑥

Answer:

1

90) lim𝑥→2⁡𝑒2⁢𝑥−𝑥2

91) lim𝑥→1⁡2−7⁢𝑥𝑥+6

Answer:

−57

92) lim𝑥→3⁡ln⁡𝑒3⁢𝑥

---

In the following exercises, use direct substitution to show that each limit leads to the indeterminate form 0/0. Then, evaluate the limit.

93) lim𝑥→4⁡𝑥2−16𝑥−4

Answer:

lim𝑥→4⁡𝑥2−16𝑥−4 =16−164−4 =00;𝑡⁢ℎ⁡𝑒⁢𝑛,lim𝑥→4⁡𝑥2−16𝑥−4 =lim𝑥→4⁡(𝑥+4)⁢(𝑥−4)𝑥−4 =8

94) lim𝑥→2⁡𝑥−2𝑥2−2⁢𝑥

95) lim𝑥→6⁡3⁢𝑥−182⁢𝑥−12

Answer:

lim𝑥→6⁡3⁢𝑥−182⁢𝑥−12 =18−1812−12 =00

then, lim𝑥→6⁡3⁢𝑥−182⁢𝑥−12 =lim𝑥→6⁡3⁢(𝑥−6)2⁢(𝑥−6) =32

96) limℎ→0⁡(1+ℎ)2−1ℎ

97) lim𝑡→9⁡𝑡−9√𝑡−3

Answer:

lim𝑥→9⁡𝑡−9√𝑡−3 =9−93−3 =00;𝑡⁢ℎ⁡𝑒⁢𝑛,lim𝑡→9⁡𝑡−9√𝑡−3 =lim𝑡→9⁡𝑡−9√𝑡−3⁢√𝑡+3√𝑡+3 =lim𝑡→9⁡(√𝑡 +3) =6

98) limℎ→0⁡1𝑎+ℎ−1𝑎ℎ, where a is a real-valued constant

99) lim𝜃→𝜋⁡sin⁡𝜃tan⁡𝜃

Answer:

lim𝜃→𝜋⁡sin⁡𝜃tan⁡𝜃 =sin⁡𝜋tan⁡𝜋 =00;𝑡⁢ℎ⁡𝑒⁢𝑛,lim𝜃→𝜋⁡sin⁡𝜃tan⁡𝜃 =lim𝜃→𝜋⁡sin⁡𝜃sin⁡𝜃cos⁡𝜃 =lim𝜃→𝜋⁡cos⁡𝜃 =−1

100) lim𝑥→1⁡𝑥3−1𝑥2−1

101) lim𝑥→1/2⁡2⁢𝑥2+3⁢𝑥−22⁢𝑥−1

Answer:

lim𝑥→1/2⁡2⁢𝑥2+3⁢𝑥−22⁢𝑥−1 =12+32−21−1 =00;𝑡⁢ℎ⁡𝑒⁢𝑛,lim𝑥→1/2⁡2⁢𝑥2+3⁢𝑥−22⁢𝑥−1 =lim𝑥→1/2⁡𝑓⁡𝑟⁢𝑎⁢𝑐⁢(2⁢𝑥−1)⁢(𝑥+2)⁢2⁢𝑥−1 =52

102) lim𝑥→−3⁡√𝑥+4−1𝑥+3

---

In the following exercises, use direct substitution to obtain an undefined expression. Then, use the method of Example to simplify the function to help determine the limit.

103) lim𝑥→−2−⁡2⁢𝑥2+7⁢𝑥−4𝑥2+𝑥−2

Answer:

−∞

104) lim𝑥→−2+⁡2⁢𝑥2+7⁢𝑥−4𝑥2+𝑥−2

105) lim𝑥→1−⁡2⁢𝑥2+7⁢𝑥−4𝑥2+𝑥−2

Answer:

−∞

106) lim𝑥→1+⁡2⁢𝑥2+7⁢𝑥−4𝑥2+𝑥−2

---

In the following exercises, assume that lim𝑥→6⁡𝑓⁡(𝑥) =4,lim𝑥→6⁡𝑔⁡(𝑥) =9, and lim𝑥→6⁡ℎ⁡(𝑥) =6. Use these three facts and the limit laws to evaluate each limit

107) lim𝑥→6⁡2⁢𝑓⁡(𝑥)⁢𝑔⁡(𝑥)

Answer:

lim𝑥→6⁡2⁢𝑓⁡(𝑥)⁢𝑔⁡(𝑥) =2⁢lim𝑥→6⁡𝑓⁡(𝑥)⁢lim𝑥→6⁡𝑔⁡(𝑥) =72

108) lim𝑥→6⁡𝑔⁡(𝑥)−1𝑓⁡(𝑥)

109) lim𝑥→6⁡(𝑓⁡(𝑥) +13⁢𝑔⁡(𝑥))

Answer:

lim𝑥→6⁡(𝑓⁡(𝑥) +13⁢𝑔⁡(𝑥)) =lim𝑥→6⁡𝑓⁡(𝑥) +13⁢lim𝑥→6⁡𝑔⁡(𝑥) =7\

110) lim𝑥→6⁡(ℎ⁡(𝑥))32

111) lim𝑥→6⁡√𝑔⁡(𝑥)−𝑓⁡(𝑥)

Answer:

lim𝑥→6⁡√𝑔⁡(𝑥)−𝑓⁡(𝑥) =√lim𝑥→6⁡𝑔⁡(𝑥)−lim𝑥→6⁡𝑓⁡(𝑥) =√5

112) lim𝑥→6⁡𝑥 ⋅ℎ⁡(𝑥)

113) lim𝑥→6⁡[(𝑥 +1) ⋅𝑓⁡(𝑥)]

Answer:

lim𝑥→6⁡[(𝑥 +1)⁢𝑓⁡(𝑥)] =(lim𝑥→6⁡(𝑥 +1))(lim𝑥→6⁡𝑓⁡(𝑥)) =28

114) lim𝑥→6⁡(𝑓⁡(𝑥) ⋅𝑔⁡(𝑥) −ℎ⁡(𝑥))

---

[T] In the following exercises, use the definition of the piecewise-defined function to evaluate the given limits (you may want to draw the graph).

115) 𝑓⁡(𝑥) ={𝑥2𝑥≤3,𝑥+4𝑥>3

1. a. lim𝑥→3−⁡𝑓⁡(𝑥)
2. b. lim𝑥→3+⁡𝑓⁡(𝑥)
3. c. lim𝑥→3⁡𝑓⁡(𝑥)

Answer:

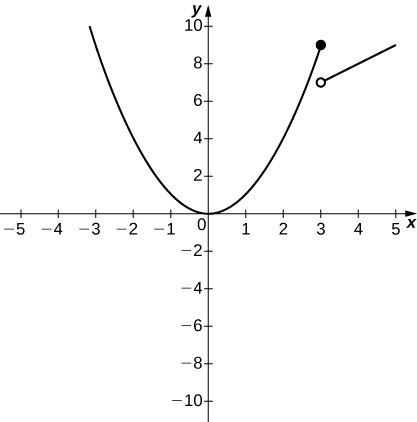
a. 9; b. 7; c. DNE

.

116) 𝑔⁡(𝑥) ={𝑥3−1𝑥≤01𝑥>0

1. a. lim𝑥→0−⁡𝑔⁡(𝑥)
2. b. lim𝑥→0+⁡𝑔⁡(𝑥)
3. c. lim𝑥→0⁡𝑔⁡(𝑥)

117) ℎ⁡(𝑥) ={𝑥2−2⁢𝑥+1𝑥<23−𝑥𝑥≥2

1. a. lim𝑥→2−⁡ℎ⁡(𝑥)
2. b. lim𝑥→2+⁡ℎ⁡(𝑥)
3. c. lim𝑥→2⁡ℎ⁡(𝑥)

Answer:

a. 1; b. 1; c. 1

---

In the following exercises, use the following graphs and the limit laws to evaluate each limit.

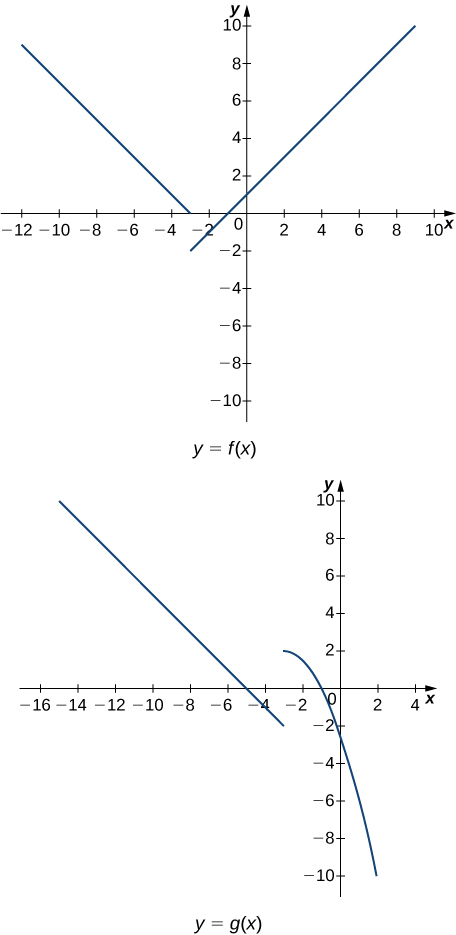
118) lim𝑥→−3+⁡(𝑓⁡(𝑥) +𝑔⁡(𝑥))

119) lim𝑥→−3−⁡(𝑓⁡(𝑥) −3⁢𝑔⁡(𝑥))

Answer:

lim𝑥→−3−⁡(𝑓⁡(𝑥) −3⁢𝑔⁡(𝑥)) =lim𝑥→−3−⁡𝑓⁡(𝑥) −3⁢lim𝑥→−3−⁡𝑔⁡(𝑥) =0 +6 =6

120) lim𝑥→0⁡𝑓⁡(𝑥)⁢𝑔⁡(𝑥)3

121) lim𝑥→−5⁡2+𝑔⁡(𝑥)𝑓⁡(𝑥)

Answer:

lim𝑥→−5⁡2+𝑔⁡(𝑥)𝑓⁡(𝑥) =2+(lim𝑥→−5⁡𝑔⁡(𝑥))lim𝑥→−5⁡𝑓⁡(𝑥) =2+02 =1

122) lim𝑥→1⁡(𝑓⁡(𝑥))2

123) lim𝑥→1⁡√𝑓⁡(𝑥)−𝑔⁡(𝑥)

Answer:

lim𝑥→1⁡3√𝑓⁡(𝑥)−𝑔⁡(𝑥) =3√lim𝑥→1⁡𝑓⁡(𝑥)−lim𝑥→1⁡𝑔⁡(𝑥) =3√2+5 =3√7

124) lim𝑥→−7⁡(𝑥 ⋅𝑔⁡(𝑥))

125) lim𝑥→−9⁡[𝑥 ⋅𝑓⁡(𝑥) +2 ⋅𝑔⁡(𝑥)]

Answer:

lim𝑥→−9⁡(𝑥⁢𝑓⁡(𝑥) +2⁢𝑔⁡(𝑥)) =(lim𝑥→−9⁡𝑥)(lim𝑥→−9⁡𝑓⁡(𝑥))+2⁢lim𝑥→−9⁡(𝑔⁡(𝑥)) =(−9)⁢(6) +2⁢(4) =−46

---

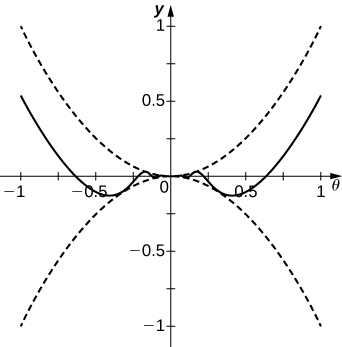
For the following problems, evaluate the limit using the squeeze theorem. Use a calculator to graph the functions 𝑓⁡(𝑥),𝑔⁡(𝑥), and ℎ⁡(𝑥) when possible.

126) [T] True or False? If 2⁢𝑥 −1 ≤𝑔⁡(𝑥) ≤𝑥2 −2⁢𝑥 +3, then lim𝑥→2⁡𝑔⁡(𝑥) =0.

127) [T] lim𝜃→0⁡𝜃2⁢cos⁡(1𝜃)

Answer:

The limit is zero.

128) lim𝑥→0⁡𝑓⁡(𝑥), where 𝑓⁡(𝑥) ={0𝑥⁢𝑟⁢𝑎⁢𝑡⁢𝑖⁢𝑜⁢𝑛⁢𝑎⁢𝑙𝑥2𝑥⁢𝑖⁢𝑟⁢𝑟⁢𝑟⁢𝑎⁢𝑡⁢𝑖⁢𝑜⁢𝑛⁢𝑎⁢𝑙

129) [T] In physics, the magnitude of an electric field generated by a point charge at a distance r in vacuum is governed by Coulomb’s law: 𝐸⁡(𝑟) =𝑞4⁢𝜋⁢𝜀⁢02𝑟, where E represents the magnitude of the electric field, q is the charge of the particle, r is the distance between the particle and where the strength of the field is measured, and \frac{1}{4πε_0} is Coulomb’s constant: 8.988 ×109 N⋅m2/C2.

a. Use a graphing calculator to graph 𝐸⁡(𝑟) given that the charge of the particle is 𝑞 =10−10.

b. Evaluate lim𝑟→0+⁡𝐸⁡(𝑟). What is the physical meaning of this quantity? Is it physically relevant? Why are you evaluating from the right?

Answer:

a

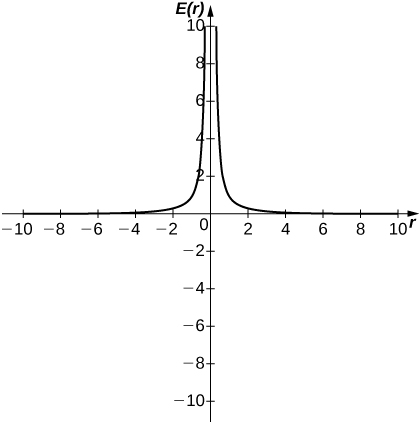
b. ∞. The magnitude of the electric field as you approach the particle q becomes infinite. It does not make physical sense to evaluate negative distance.

130) [T] The density of an object is given by its mass divided by its volume: 𝜌 =𝑚/𝑉.

a. Use a calculator to plot the volume as a function of density (𝑉 =𝑚/𝜌), assuming you are examining something of mass 8 kg (𝑚 =8).

b. Evaluate lim𝑥→0+⁡𝑉⁡(𝜌) and explain the physical meaning.

---

Chapter Review Exercises

212) Using the graph, find each limit or explain why the limit does not exist.

a. lim𝑥→−1⁡𝑓⁡(𝑥)

b. lim𝑥→1⁡𝑓⁡(𝑥)

c. lim𝑥→0+⁡𝑓⁡(𝑥)

d. lim𝑥→2⁡𝑓⁡(𝑥)

---

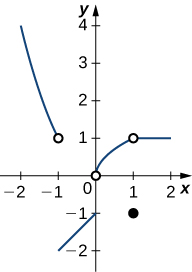
In the following exercises, evaluate the limit algebraically or explain why the limit does not exist.

213) lim𝑥→2⁡2⁢𝑥2−3⁢𝑥−2𝑥−2

Answer:

5

214) lim𝑥→0⁡3⁢𝑥2 −2⁢𝑥 +4

215) lim𝑥→3⁡𝑥3−2⁢𝑥2−13⁢𝑥−2

Answer:

8/7

216) lim𝑥→𝜋/2⁡𝑐⁢𝑜⁢𝑡⁢𝑥𝑐⁢𝑜⁢𝑠⁢𝑥 This is covered in section 2.4

217) lim𝑥→−5⁡𝑥2+25𝑥+5

Answer:

DNE

218) lim𝑥→2⁡3⁢𝑥2−2⁢𝑥−8𝑥2−4

219) lim𝑥→1⁡𝑥2−1𝑥3−1

Answer:

2/3

220) lim𝑥→1⁡𝑥2−1√𝑥−1

221) \displaystyle 𝑙⁢𝑖⁢𝑚𝑥→4⁢4−𝑥√𝑥−2

Answer:

−4

222) lim𝑥→4⁡1√𝑥−2

---

In the following exercises, use the squeeze theorem to prove the limit.

223) lim𝑥→0⁡𝑥2⁢𝑐⁢𝑜⁢𝑠⁡(2⁢𝜋⁢𝑥) =0

Answer:

Since −1 ≤𝑐⁢𝑜⁢𝑠⁡(2⁢𝜋⁢𝑥) ≤1, then −𝑥2 ≤𝑥2⁢𝑐⁢𝑜⁢𝑠⁡(2⁢𝜋⁢𝑥) ≤𝑥2. Since 𝑙⁢𝑖⁢𝑚𝑥→0⁢𝑥2 =0 =𝑙⁢𝑖⁢𝑚𝑥→0 −𝑥2, it follows that 𝑙⁢𝑖⁢𝑚𝑥→0⁢𝑥2⁢𝑐⁢𝑜⁢𝑠⁡(2⁢𝜋⁢𝑥) =0.

224) lim𝑥→0⁡𝑥3⁢𝑠⁢𝑖⁢𝑛⁡(𝜋𝑥) =0