3.E: Solving Linear Systems
- Page ID
- 6401
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise \(\PageIndex{1}\)
Determine whether or not the given ordered pair is a solution to the given system.
1. \(\left( \frac { 2 } { 3 } , - 4 \right)\);
\(\left\{ \begin{array} { l } { 9 x - y = 10 } \\ { 3 x + 4 y = - 14 } \end{array} \right.\)
2. \(\left( - \frac { 1 } { 2 } , \frac { 3 } { 4 } \right)\);
\(\left\{ \begin{array} { l } { 6 x - 8 y = - 9 } \\ { x + 2 y = 1 } \end{array} \right.\)
3. \(\left( - 5 , - \frac { 7 } { 8 } \right)\);
\(\left\{ \begin{array} { l } { x - 16 y = 9 } \\ { 2 x - 8 y = - 17 } \end{array} \right.\)
4. \(\left( - 1 , \frac { 4 } { 5 } \right)\);
\(\left\{ \begin{array} { l } { 2 x + 5 y = 2 } \\ { 3 x - 10 y = - 5 } \end{array} \right.\)
- Answer
-
1. Yes
3. No
Exercise \(\PageIndex{2}\)
Given the graphs, determine the simultaneous solution.
1.
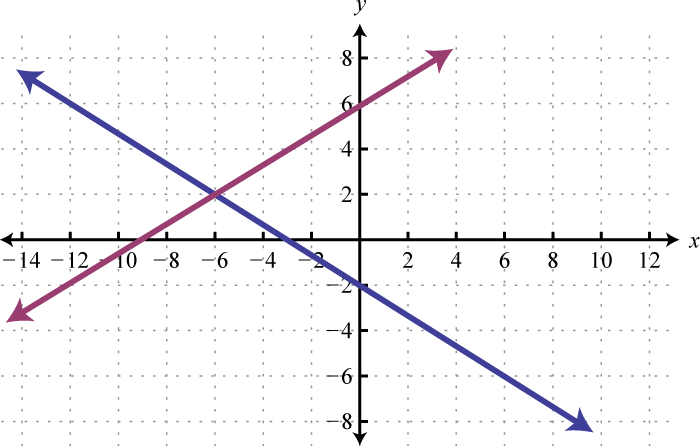
2.
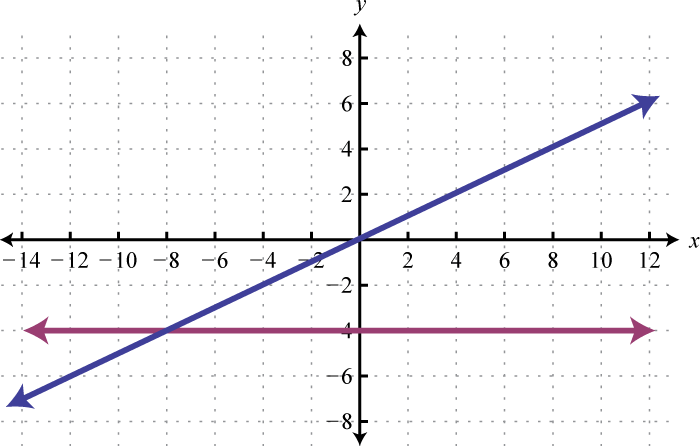
3.
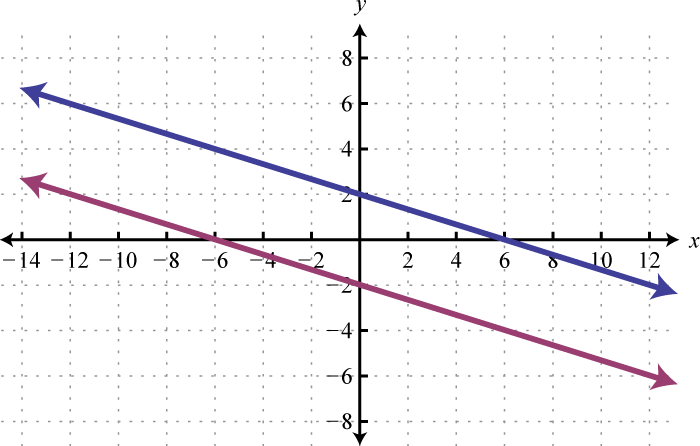
4.
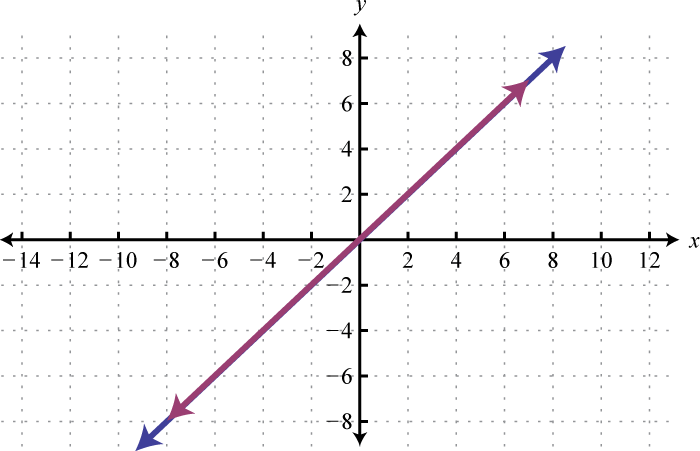
- Answer
-
1. \((-6, 2)\)
3. \(\varnothing\)
Exercise \(\PageIndex{3}\)
Solve by graphing.
- \(\left\{ \begin{array} { l } { 2 x + y = 6 } \\ { x - 2 y = 8 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 5 x - 2 y = 0 } \\ { x - y = 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 4 x + 3 y = - 12 } \\ { - 8 x - 6 y = 24 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { \frac { 1 } { 2 } x + 2 y = 6 } \\ { x + 4 y = - 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 5 x + 2 y = 30 } \\ { y - 5 = 0 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 5 x + 3 y = - 15 } \\ { x + 3 = 0 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { \frac { 1 } { 3 } x - \frac { 1 } { 2 } y = 2 } \\ { \frac { 1 } { 2 } x + \frac { 3 } { 5 } y = 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { \frac { 2 } { 5 } x + \frac { 1 } { 2 } y = 1 } \\ { \frac { 1 } { 15 } x + \frac { 1 } { 6 } y = - \frac { 1 } { 3 } } \end{array} \right.\)
- Answer
-
1. \((4, -2)\)
3. \(\left( x , - \frac { 4 } { 3 } x - 4 \right)\)
5. \((4,5)\)
7. \((6,0)\)
Exercise \(\PageIndex{4}\)
Solve by substitution.
- \(\left\{ \begin{array} { l } { 4 x - y = 12 } \\ { x + 3 y = - 10 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 9 x - 2 y = 3 } \\ { x - 3 y = 17 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 12 x + y = 7 } \\ { 3 x - 4 y = 6 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 3 x - 2 y = 1 } \\ { 2 x + 3 y = - 1 } \end{array} \right.\)
- Answer
-
1. \((2,-4)\)
3. \(\left( \frac { 2 } { 3 } , - 1 \right)\)
Exercise \(\PageIndex{5}\)
Solve by elimination.
- \(\left\{ \begin{array} { l } { 5 x - 2 y = - 12 } \\ { 4 x + 6 y = - 21 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 4 x - 5 y = 12 } \\ { 8 x + 3 y = - 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 5 x - 3 y = 11 } \\ { 2 x - 4 y = - 4 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 7 x + 2 y = 3 } \\ { 3 x + 5 y = - 7 } \end{array} \right.\)
- Answer
-
1. \(\left( - 3 , - \frac { 3 } { 2 } \right)\)
3. \((4,3)\)
Exercise \(\PageIndex{6}\)
Solve using any method.
- \(\left\{ \begin{array} { l } { 4 x - 8 y = 4 } \\ { x + 2 y = 9 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 6 x - 9 y = 8 } \\ { x - y = 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 2 x - 6 y = - 1 } \\ { 6 x + 10 y = - 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 2 x - 3 y = 36 } \\ { x - 3 y = 9 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 5 x - 3 y = 10 } \\ { - 10 x + 6 y = 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { \frac { 1 } { 2 } x - y = 3 } \\ { 3 x - 6 y = 18 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { \frac { 3 } { 5 } x - \frac { 1 } { 2 } y = - 1 } \\ { \frac { 1 } { 10 } x + \frac { 3 } { 4 } y = - 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { \frac { 4 } { 3 } x - \frac { 2 } { 5 } y = - \frac { 8 } { 15 } } \\ { \frac { 1 } { 2 } x - \frac { 2 } { 3 } y = - \frac { 11 } { 24 } } \end{array} \right.\)
- Answer
-
1. \((5,2)\)
3. \(\left( - \frac { 1 } { 2 } , 0 \right)\)
5. \(\varnothing\)
7. \(\left( - \frac { 5 } { 2 } , - 1 \right)\)
Exercise \(\PageIndex{7}\)
Set up a linear system and solve.
- The sum of two integers is \(32\). The larger is \(4\) less than twice the smaller. Find the integers.
- The sum of \(2\) times a larger integer and \(3\) times a smaller integer is \(54\). When twice the smaller integer is subtracted from the larger, the result is \(−1\). Find the integers.
- The length of a rectangle is \(2\) centimeters less than three times its width and the perimeter measures \(44\) centimeters. Find the dimensions of the rectangle.
- The width of a rectangle is one-third of its length. If the perimeter measures \(53 \frac{1}{3}\) centimeters, then find the dimensions of the rectangle.
- The sum of a larger integer and \(3\) times a smaller is \(61\). When twice the smaller integer is subtracted from the larger, the result is \(1\). Find the integers.
- A total of \($8,600\) was invested in two accounts. One account earned \(4 \frac{3}{4}\)% annual interest and the other earned \(6 \frac{1}{2}\)% annual interest. If the total interest for one year was \($431.25\), how much was invested in each account?
- A jar consisting of only nickels and dimes contains \(76\) coins. If the total value is \($6\), how many of each coin are in the jar?
- A nurse wishes to obtain \(32\) ounces of a \(1.2\)% saline solution. How much of a \(1\)% saline solution must she mix with a \(2.6\)% saline solution to achieve the desired mixture?
- A light aircraft flying with the wind can travel \(330\) miles in \(2\) hours. The aircraft can fly the same distance against the wind in \(3\) hours. Find the speed of the wind.
- An executive was able to average \(52\) miles per hour to the airport in her car and then board an airplane that averaged \(340\) miles per hour. If the total \(640\)-mile business trip took \(4\) hours, how long did she spend on the airplane?
- Answer
-
1. \(12, 20\)
3. Length: \(16\) centimeters; width: \(6\) centimeters
5. \(12, 25\)
7. The jar contains \(32\) nickels and \(44\) dimes.
9. \(27.5\) miles per hour
Exercise \(\PageIndex{8}\)
Determine whether the given ordered triple is a solution to the given system.
1. \((-2,-1,3)\);
\(\left\{ \begin{array} { l } { 4 x - y + 2 z = - 1 } \\ { x - 4 y + 3 z = 11 } \\ { 3 x + 5 y - 4 z = 1 } \end{array} \right.\)
2. \((5,-3,-2)\);
\(\left\{ \begin{array} { l } { x - 4 y + 6 z = 5 } \\ { 2 x + 5 y - z = - 3 } \\ { 3 x - 4 y + z = 25 } \end{array} \right.\)
3. \(\left( 1 , - \frac { 3 } { 2 } , - \frac { 4 } { 3 } \right)\);
\(\left\{ \begin{array} { l } { 5 x - 4 y + 3 z = 7 } \\ { x + 2 y - 6 z = 6 } \\ { 12 x - 6 y + 6 z = 13 } \end{array} \right.\)
4. \(\left( \frac { 5 } { 4 } , - \frac { 1 } { 3 } , 2 \right)\);
\(\left\{ \begin{array} { c } { 8 x + 9 y + z = 9 } \\ { 4 x + 12 y - 4 z = - 7 } \\ { 12 x - 6 y - z = - 5 } \end{array} \right.\)
- Answer
-
1. No
3. Yes
Exercise \(\PageIndex{9}\)
Solve.
- \(\left\{ \begin{array} { c } { 2 x + 3 y - z = 1 } \\ { 5 y + 2 z = 12 } \\ { 3 z = 18 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { 3 x - 5 y - 2 z = 21 } \\ { y - 7 z = 18 } \\ { 4 z = - 12 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 4 x - 5 y - z = - 6 } \\ { 3 x + 6 y + 5 z = 3 } \\ { 5 x - 2 y - 3 z = - 17 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x - 6 y + 3 z = - 2 } \\ { 5 x + 4 y - 2 z = 24 } \\ { 6 x - 8 y - 5 z = 25 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x + 2 y - 2 z = 1 } \\ { 2 x - y - z = - 2 } \\ { 6 x - 3 y - 3 z = 12 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 3 x + y + 2 z = - 1 } \\ { 9 x + 3 y + 6 z = - 3 } \\ { 4 x + y + 4 z = - 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { 3 a - 2 b + 5 c = - 3 } \\ { 6 a + 4 b - c = - 2 } \\ { - 6 a + 6 b + 24 c = 7 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { 9 a - 2 b - 6 c = 10 } \\ { 5 a - 3 b - 10 c = 14 } \\ { - 3 a + 4 b + 12 c = - 20 } \end{array} \right.\)
- Answer
-
1. \(\left( \frac { 7 } { 2 } , 0,6 \right)\)
3. \((-2,-1,3)\)
5. \(\varnothing\)
7. \(\left( - \frac { 2 } { 3 } , \frac { 1 } { 2 } , 0 \right)\)
Exercise \(\PageIndex{10}\)
Set up a linear system and solve.
- The sum of three integers is \(24\). The larger is equal to the sum of the two smaller integers. Three times the smaller is equal to the larger. Find the integers.
- The sports center sold \(120\) tickets to the Friday night basketball game for a total of \($942\). A general admission ticket cost \($12\), a student ticket cost \($6\), and a child ticket cost \($4\). If the sum of the general admission and student tickets totaled \(105\), then how many of each ticket were sold?
- A \(16\)-ounce mixed nut product containing \(13.5\)% peanuts is to be packaged. The packager has a three-mixed nut product containing \(6\)%, \(10\)%, and \(50\)% peanut concentrations in stock. If the amount of \(50\)% peanut product is to be one-quarter that of the \(10\)% peanut product, then how much of each will be needed to produce the desired peanut concentration?
- Water is to be mixed with two acid solutions to produce a \(25\)-ounce solution containing \(6\)% acid. The acid mixtures on hand contain \(10\)% and \(25\)% acid. If the amount of \(25\)% acid is to be one-half the amount of the \(10\)% acid solution, how much water will be needed?
- Answer
-
1. \(4,8,12\)
3. \(6\) oz of the \(6\)% peanut stock, \(8\) oz of the \(10\)% peanut stock, and \(2\) oz of the \(50\)% peanut stock should be mixed.
Exercise \(\PageIndex{11}\)
Construct the corresponding augmented matrix.
- \(\left\{ \begin{array} { l } { 9 x - 7 y = 4 } \\ { 3 x - y = - 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { x - 5 y = 12 } \\ { 3 y = - 5 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x - y + 2 z = - 6 } \\ { 3 x - 6 y - z = 3 } \\ { - x + y - 5 z = 10 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { 5 x + 7 y - z = 0 } \\ { - 8 y + z = - 1 } \\ { - x + 3 z = - 9 } \end{array} \right.\)
- Answer
-
1. \(\left[ \begin{array} { r r | r } { 9 } & { - 7 } & { 4 } \\ { 3 } & { - 1 } & { - 1 } \end{array} \right]\)
3. \(\left[ \begin{array} { r r r | r } { 1 } & { - 1 } & { 2} &{- 6 } \\ { 3 } & { - 6 } & { - 1} & { 3 } \\ { - 1 } & { 1 } & { - 5 } & { 10 } \end{array} \right]\)
Exercise \(\PageIndex{12}\)
Solve using matrices and Gaussian elimination.
- \(\left\{ \begin{array} { l } { 4 x + 5 y = 0 } \\ { 2 x - 3 y = 22 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 3 x - 8 y = 20 } \\ { 2 x + 5 y = 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { x - y + 4 z = 1 } \\ { - 2 x + 3 y - 2 z = 0 } \\ { x - 6 y + 8 z = 8 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { - x + 3 y - z = 1 } \\ { 3 x - 6 y + 2 z = - 4 } \\ { 4 x - 3 y + 2 z = - 7 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 5 x - 3 y - z = 2 } \\ { x - 6 y + z = 7 } \\ { 2 x + 6 y - 2 z = - 8 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x + 2 y + 3 z = 4 } \\ { x + 3 y + z = 3 } \\ { 2 x + 5 y + 4 z = 8 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { 2 a + 5 b - c = 4 } \\ { 2 a + c = - 2 } \\ { a + b + 3 c = 6 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { a + 2 b + 3 c = - 7 } \\ { 4 b - 2 c = 8 } \\ { 3 a - c = - 7 } \end{array} \right.\)
- Answer
-
1. \((5,-4)\)
3. \(\left( - 2 , - 1 , \frac { 1 } { 2 } \right)\)
5. \(\left( x , \frac { 2 } { 3 } x - 1,3 x + 1 \right)\)
7. \((-2,2,2)\)
Exercise \(\PageIndex{13}\)
Calculate the determinant.
- \(\left| \begin{array} { c c} { - 9}&{5 } \\ { - 1}&{3 } \end{array} \right|\)
- \(\left| \begin{array} { c c } { - 5}&{5 } \\ { - 3}&{3 } \end{array} \right|\)
- \(\left| \begin{array} { c c } { 0}&{7 } \\ { 2}&{3 } \end{array} \right|\)
- \(\left| \begin{array} { l l } { 0 } & { b _ { 1 } } \\ { a _ { 2 } }&{b _ { 2 } } \end{array} \right|\)
- \(\left| \begin{array} { r r r } { 2 } & { - 3 } & { 0 } \\ { 1 } & { - 2 } & { - 1 } \\ { 0 } & { 1 } & { 3 } \end{array} \right|\)
- \(\left| \begin{array} { r r r } { 3 } & { 2 } & { - 1 } \\ { 1 } & { - 1 } & { 0 } \\ { 5 } & { - 2 } & { - 4 } \end{array} \right|\)
- \(\left| \begin{array} { r r r } { 5 } & { - 3 } & { - 1 } \\ { 1 } & { - 6 } & { 1 } \\ { 2 } & { 6 } & { - 2 } \end{array} \right|\)
- \(\left| \begin{array} { l l l } { a _ { 1 } } & { 0 } & { 0 } \\ { a _ { 2 } } & { b _ { 2 } } & { 0 } \\ { a _ { 3 } } & { b _ { 3 } } & { c _ { 3 } } \end{array} \right|\)
- Answer
-
1. \(-22\)
3. \(-14\)
5. \(-1\)
7. \(0\)
Exercise \(\PageIndex{14}\)
Solve using Cramer's rule.
- \(\left\{ \begin{array} { l } { 2 x - 3 y = - 4 } \\ { 3 x + 5 y = 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { 3 x - y = 2 } \\ { - 2 x + 6 y = 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 3 x + 5 y = 6 } \\ { 6 x + y = - 6 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 6 x - 4 y = - 1 } \\ { - 3 x + 2 y = 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 5 x + 2 y + 4 z = 4 } \\ { 4 x + 3 y + 2 z = - 5 } \\ { - 5 x - 3 y - 5 z = 0 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 2 x - y + 2 z = 1 } \\ { x - 3 y + z = 2 } \\ { 3 x - y - 4 z = - 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 4 x - y - 2 z = - 7 } \\ { 2 x + y + 6 z = 0 } \\ { 2 x + 2 y + 4 z = - 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { x - y - z = 1 } \\ { 2 x - y + 3 z = 2 } \\ { x + y + z = - 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 4 x - y + 2 z = - 1 } \\ { 2 x + 3 y - z = 3 } \\ { 6 x + 2 y + z = 2 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x - y + 2 z = 1 } \\ { 2 x + 2 y - z = 2 } \\ { 3 x + y + z = 1 } \end{array} \right.\)
- Answer
-
1. \(\left( - \frac { 17 } { 19 } , \frac { 14 } { 19 } \right)\)
3. \(\left( - \frac { 4 } { 3 } , 2 \right)\)
5. \((2,-5,1)\)
7. \(\left( - \frac { 3 } { 2 } , 0 , \frac { 1 } { 2 } \right)\)
9. \(\left( x , - \frac { 8 } { 5 } x + 1 , - \frac { 14 } { 5 } x \right)\)
Exercise \(\PageIndex{15}\)
Determine whether or not the given point is a solution to the system of inequalities.
1. \((-6,1)\);
\(\left\{ \begin{array} { l } { - x + y > 2 } \\ { x - 2 y \leq - 1 } \end{array} \right.\)
2. \(\left( \frac { 1 } { 2 } , - 3 \right)\);
\(\left\{ \begin{array} { l } { 4 x - 2 y \geq 8 } \\ { 6 x + 2 y < - 3 } \end{array} \right.\)
3. \((-4,-2)\);
\(\left\{ \begin{array} { l } { x - y > - 3 } \\ { 2 x + 3 y \leq 0 } \\ { - 3 x + 4 y \geq 4 } \end{array} \right.\)
4. \(\left( 5 , - \frac { 1 } { 5 } \right)\)'
\(\left\{ \begin{array} { l } { y < x ^ { 2 } - 25 } \\ { y > \frac { 2 } { 3 } x - 1 } \end{array} \right.\)
5. \((-3,-2)\);
\(\left\{ \begin{array} { l } { y < ( x - 1 ) ^ { 2 } } \\ { y \leq | x + 1 | - 3 } \end{array} \right.\)
6. \(\left( 2 , - \frac { 2 } { 3 } \right)\);
\(\left\{ \begin{array} { l } { y < 0 } \\ { x ^ { 2 } + y \geq 3 } \end{array} \right.\)
- Answer
-
1. Yes
3. Yes
5. Yes
Exercise \(\PageIndex{16}\)
Graph the solution set.
- \(\left\{ \begin{array} { l } { y \leq - 4 } \\ { x - 2 y > 8 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x + 4 y > 8 } \\ { 2 x - y \leq 4 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y - 3 < 0 } \\ { - 2 x + 3 y > - 9 } \\ { x + y \geq 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y \leq 0 } \\ { 2 x - 6 y < 9 } \\ { - 2 x + 6 y < 9 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 2 x + y < 3 } \\ { y > ( x - 2 ) ^ { 2 } - 5 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y > | x | } \\ { y \geq - x ^ { 2 } + 6 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x - 2 y < 12 } \\ { y \leq ( x - 4 ) ^ { 3 } } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { y + 6 > 0 } \\ { y < \sqrt { x } } \end{array} \right.\)
- Answer
-
1.
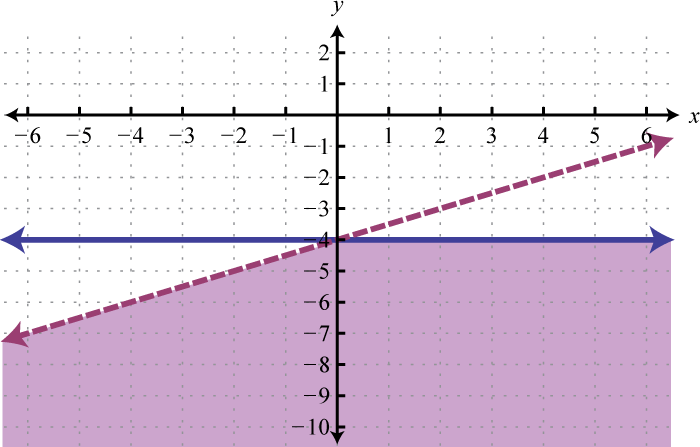
Figure 3.E.5 3.
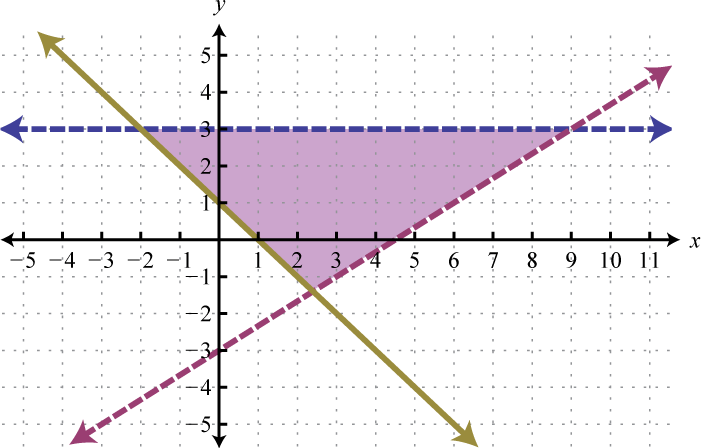
Figure 3.E.6 5.
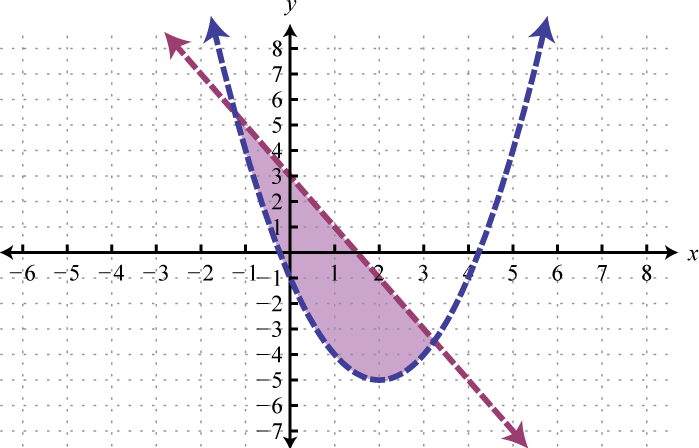
Figure 3.E.7 7.
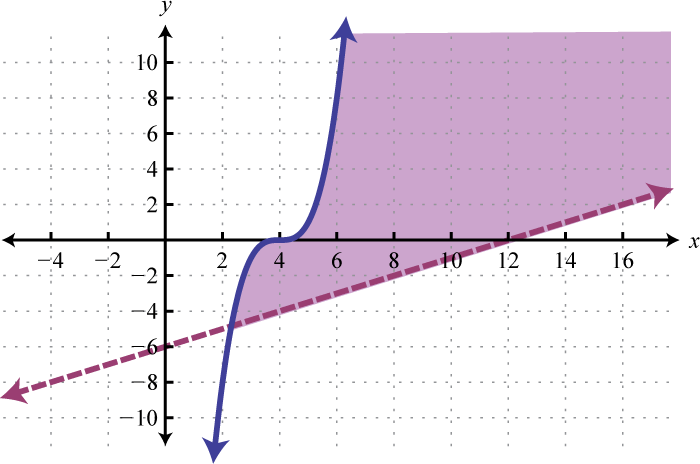
Figure 3.E.8
Sample Exam
Exercise \(\PageIndex{17}\)
- Determine whether or not \((-2, \frac{3}{4})\) is a solution to \(\left\{ \begin{array} { l } { 2 x - 8 y = - 10 } \\ { 3 x + 4 y = - 3 } \end{array} \right.\).
- Determine whether or not \((−3, 2, −5)\) is a solution to \(\left\{ \begin{array} { l } { x - y + 2 z = - 15 } \\ { 2 x - 3 y + z = - 17 } \\ { 3 x + 5 y - 2 z = 10 } \end{array} \right.\).
- Answer
-
1. Yes
Exercise \(\PageIndex{18}\)
Solve by graphing.
- \(\left\{ \begin{array} { l } { x - y = - 5 } \\ { x + y = - 3 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 6 x - 8 y = 48 } \\ { \frac { 1 } { 2 } x - \frac { 2 } { 3 } y = 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { \frac { 1 } { 2 } x + y = - 6 } \\ { - 2 x - 4 y = 24 } \end{array} \right.\)
- Answer
-
1. \((-4,1)\)
3. \(\left( x , - \frac { 1 } { 2 } x - 6 \right)\)
Exercise \(\PageIndex{19}\)
Solve by substitution.
- \(\left\{ \begin{array} { l } { x - 8 y = 10 } \\ { 3 x + 2 y = 17 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { \frac { 3 } { 2 } x - \frac { 1 } { 6 } y = - \frac { 23 } { 2 } } \\ { \frac { 3 } { 8 } x + \frac { 5 } { 6 } y = - \frac { 11 } { 2 } } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 5 x - y = 15 } \\ { 2 x - \frac { 2 } { 5 } y = 6 } \end{array} \right.\)
- Answer
-
2. \((-8,-3)\)
Exercise \(\PageIndex{20}\)
Solve.
- \(\left\{ \begin{array} { l } { 3 x - 5 y = 27 } \\ { 7 x + 2 y = 22 } \end{array} \right.\)
- \(\left\{ \begin{array} { c } { 12 x + 3 y = - 3 } \\ { 5 x + 2 y = 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 5 x - 3 y = - 1 } \\ { - 15 x + 9 y = 5 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 6 a - 3 b + 2 c = 11 } \\ { 2 a - b - 4 c = - 15 } \\ { 4 a - 5 b + 3 c = 23 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 4 x + y - 6 z = 8 } \\ { 5 x + 4 y - 2 z = 10 } \\ { 2 x + y - 2 z = 4 } \end{array} \right.\)
- Answer
-
1. \((4,-3)\)
3. \(\varnothing\)
5. \(\left( x , - x + 2 , \frac { 1 } { 2 } x - 1 \right)\)
Exercise \(\PageIndex{21}\)
Solve using any method.
- \(\left\{ \begin{array} { c } { x - 5 y + 8 z = 1 } \\ { 2 x + 9 y - 4 z = - 8 } \\ { - 3 x + 11 y + 12 z = 15 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 2 x - y + z = 1 } \\ { x - y + 3 z = 2 } \\ { 3 x - 2 y + 4 z = 5 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { - 5 x + 3 y = 2 } \\ { 4 x + 2 y = - 1 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { 2 x - 3 y + 2 z = 2 } \\ { x + 2 y - 3 z = 0 } \\ { - x - y + z = - 2 } \end{array} \right.\)
- Answer
-
2. \(\varnothing\)
4. \((2,2,2)\)
Exercise \(\PageIndex{22}\)
Graph the solution set.
- \(\left\{ \begin{array} { l } { 3 x + 4 y < 24 } \\ { 2 x - 3 y \leq 3 } \\ { y + 1 > 0 } \end{array} \right.\)
- \(\left\{ \begin{array} { l } { x + y < 4 } \\ { y > - ( x + 6 ) ^ { 2 } + 4 } \end{array} \right.\)
- Answer
-
2.
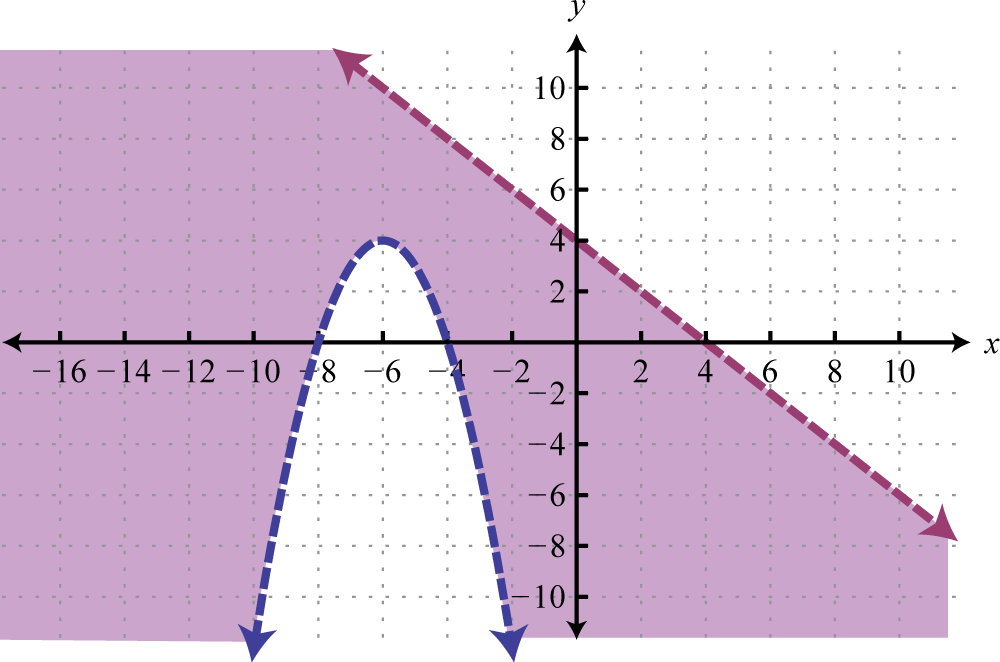
Figure 3.E.9
Exercise \(\PageIndex{23}\)
Use algebra to solve the following.
- The length of a rectangle is \(1\) inch less than twice that of its width. If the perimeter measures \(49\) inches, then find the dimensions of the rectangle.
- Joe’s \($4,000\) savings is in two accounts. One account earns \(3.1\)% annual interest and the other earns \(4.9\)% annual interest. His total interest for the year is \($174.40\). How much does he have in each account?
- One solution contains \(40\)% alcohol and another contains \(72\)% alcohol. How much of each should be mixed together to obtain \(16\) ounces of a \(62\)% alcohol solution?
- Jerry took two buses on the \(193\)-mile trip to visit his grandmother. The first bus averaged \(46\) miles per hour and the second bus was able to average \(52\) miles per hour. If the total trip took \(4\) hours, then how long was spent in each bus?
- A total of \($8,500\) was invested in three interest earning accounts. The interest rates were \(2\)%, \(3\)%, and \(6\)%. If the total simple interest for one year was \($380\) and the amount invested at \(6\)% was equal to the sum of the amounts in the other two accounts, then how much was invested in each account?
- A mechanic wishes to mix \(6\) gallons of a \(22\)% antifreeze solution. In stock he has a \(60\)% and an \(80\)% antifreeze concentrate. Water is to be added in the amount that is equal to twice the amount of both concentrates combined. How much water is needed?
- Answer
-
2. Joe has \($1,200\) in the account earning \(3.1\)% interest and \($2,800\) in the account earning \(4.9\)% interest
4. Jerry spent \(2.5\) hours in the first bus and \(1.5\) hours in the second.
6. \(4\) gallons of water is needed.


