4.E: Polynomial and Rational Functions (Exercises)
- Page ID
- 6443
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Exercise \(\PageIndex{1}\)
Evaluate
- Given \(f ( x ) = 2 x ^ { 2 } - x + 6\), find \(f ( - 3 ) , f ( 0 )\), and \(f ( 10 )\).
- Given \(g ( x ) = - x ^ { 2 } + 4 x - 1\), find \(g ( - 1 ) , g ( 0 )\), and \(g(3)\).
- Given \(h ( t ) = - t ^ { 3 } - 2 t ^ { 2 } + 3\), find \(h ( - 3 ) , h ( 0 )\), and \(h(2)\).
- Given \(p ( x ) = x ^ { 4 } - 2 x ^ { 2 } + x\), find \(p ( - 1 ) , p ( 0 )\), and \(p(2)\).
- The following graph gives the height \(h (t)\) in feet of a projectile over time \(t\) in seconds
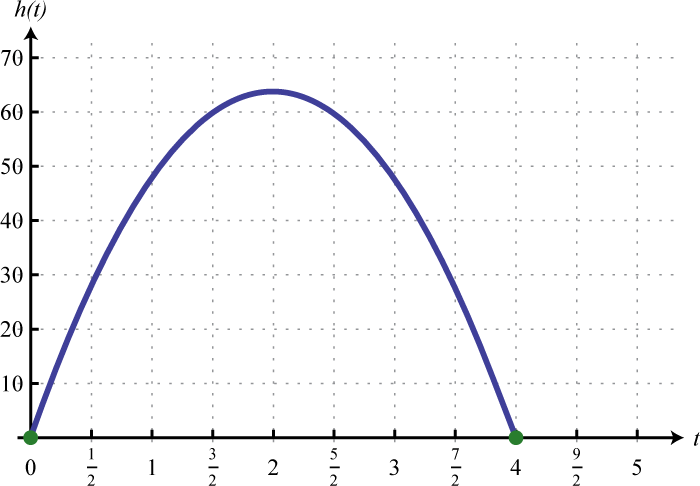
(a) Use the graph to determine the height of the projectile at \(2.5\) seconds.
(b) At what time does the projectile reach its maximum height?
(c) How long does it take the projectile to return to the ground?
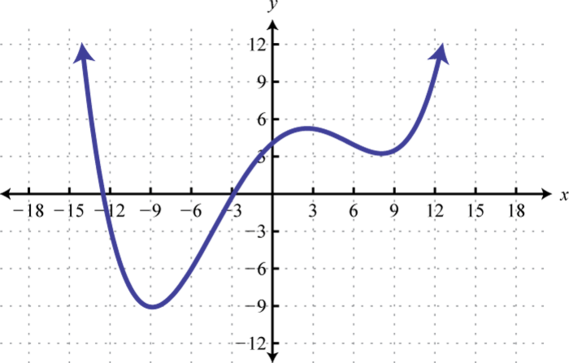
6. Given the graph of the function \(f\), find \(f ( - 9 ) , f ( - 3 )\), and \(f(12)\).
7. From the ground, a bullet is fired straight up into the air at \(340\) meters per second. Ignoring the effects of air friction, write a function that models the height of the bullet and use it to calculate the bullet’s height after one-quarter of a second. (Round off to the nearest meter.)
8. An object is tossed into the air at an initial speed of \(30\) feet per second from a rooftop \(10\) feet high. Write a function that models the height of the object and use it to calculate the height of the object after \(1\) second.
- Answer
-
1. \(f ( - 3 ) = 27 ; f ( 0 ) = 6 ; f ( 10 ) = 196\)
3. \(h ( - 3 ) = 12 ; h ( 0 ) = 3 ; h ( 2 ) = - 13\)
5. (a) \(60\) feet; (b) \(2\) seconds; (c) \(4\) seconds
7. \(h ( t ) = - 4.9 t ^ { 2 } + 340 t\); at \(0.25\) second, the bullet's height is about \(85\) meters.
Exercise \(\PageIndex{2}\)
Perform the operations.
- Given \(f ( x ) = 5 x ^ { 2 } - 3 x + 1\) and \(g ( x ) = 2 x ^ { 2 } - x - 1\), find \(( f + g ) ( x )\).
- Given \(f ( x ) = x ^ { 2 } + 3 x - 8\) and \(g ( x ) = x ^ { 2 } - 5 x - 7\), find \(( f - g ) ( x )\).
- Given \(f ( x ) = 3 x ^ { 2 } - x + 2\) and \(g ( x ) = 2 x - 3\), find \(( f \cdot g ) ( x )\).
- Given \(f ( x ) = 27 x ^ { 5 } - 15 x ^ { 3 } - 3 x ^ { 2 }\) and \(g ( x ) = 3 x ^ { 2 }\), find \(( f / g ) ( x )\).
- Given \(g ( x ) = x ^ { 2 } - x + 1\), find \(g ( - 3 u )\).
- GIven \(g ( x ) = x ^ { 3 } - 1\), find \(g ( x - 1 )\).
- Answer
-
1. \(( f + g ) ( x ) = 7 x ^ { 2 } - 4 x\)
3. \(( f \cdot g ) ( x ) = 6 x ^ { 3 } - 11 x ^ { 2 } + 7 x - 6\)
5. \(g ( - 3 u ) = 9 u ^ { 2 } + 3 u + 1\)
Exercise \(\PageIndex{3}\)
Given \(f ( x ) = 16 x ^ { 3 } - 12 x ^ { 2 } + 4 x , g ( x ) = x ^ { 2 } - x + 1\), and \(h ( x ) = 4 x\), find the following:
- \(( g \cdot h ) ( x )\)
- \(( f - g ) ( x )\)
- \(( g + f ) ( x )\)
- \(( f / h ) ( x )\)
- \(( f \cdot h ) ( - 1 )\)
- \(( g + h ) ( - 3 )\)
- \(( g - f ) ( 2 )\)
- \(( f / h ) \left( \frac { 3 } { 2 } \right)\)
- Answer
-
1. \(( g \cdot h ) ( x ) = 4 x ^ { 3 } - 4 x ^ { 2 } + 4 x\)
3. \(( g + f ) ( x ) = 16 x ^ { 3 } - 11 x ^ { 2 } + 3 x + 1\)
5. \(( f \cdot h ) ( - 1 ) = 128\)
7. \(( g - f ) ( 2 ) = - 85\)
Exercise \(\PageIndex{4}\)
Factor our the greatest common factor (GCF).
- \(2 x ^ { 4 } - 12 x ^ { 3 } - 2 x ^ { 2 }\)
- \(18 a ^ { 3 } b - 3 a ^ { 2 } b ^ { 2 } + 3 a b ^ { 3 }\)
- \(x ^ { 4 } y ^ { 3 } - 3 x ^ { 3 } y + x ^ { 2 } y\)
- \(x ^ { 3 n } - x ^ { 2 n } - x ^ { n }\)
- Answer
-
1. \(2 x ^ { 2 } \left( x ^ { 2 } - 6 x - 1 \right)\)
3. \(x ^ { 2 } y \left( x ^ { 2 } y ^ { 2 } - 3 x + 1 \right)\)
Exercise \(\PageIndex{5}\)
Factor by grouping.
- \(2 x ^ { 3 } - x ^ { 2 } + 2 x - 1\)
- \(3x ^ { 3 } - x ^ { 2 } - 6 x + 2\)
- \(x ^ { 3 } - 5 x ^ { 2 } y + x y ^ { 2 } - 5 y ^ { 3 }\)
- \(a ^ { 2 } b - a + a b ^ { 3 } - b ^ { 2 }\)
- \(2 x ^ { 4 } - 4 x y ^ { 3 } + 2 x ^ { 2 } y ^ { 2 } - 4 x ^ { 3 } y\)
- \(x ^ { 4 } y ^ { 2 } - x y ^ { 5 } + x ^ { 3 } y ^ { 4 } - x ^ { 2 } y ^ { 3 }\)
- Answer
-
1. \(\left( x ^ { 2 } + 1 \right) ( 2 x - 1 )\)
3. \(\left( x ^ { 2 } + y ^ { 2 } \right) ( x - 5 y )\)
5. \(2 x ( x - 2 y ) \left( x ^ { 2 } + y ^ { 2 } \right)\)
Exercise \(\PageIndex{6}\)
Factor the special binomials.
- \(64 x ^ { 2 } - 1\)
- \(9 - 100 y ^ { 2 }\)
- \(x ^ { 2 } - 36 y ^ { 2 }\)
- \(4 - ( 2 x - 1 ) ^ { 2 }\)
- \(a ^ { 3 } b ^ { 3 } + 125\)
- \(64 x ^ { 3 } - y ^ { 3 }\)
- \(81 x ^ { 4 } - y ^ { 4 }\)
- \(x ^ { 8 } - 1\)
- \(x ^ { 6 } - 64 y ^ { 6 }\)
- \(1 - a ^ { 6 } b ^ { 6 }\)
- Answer
-
1. \(( 8 x + 1 ) ( 8 x - 1 )\)
3. \(( x + 6 y ) ( x - 6 y )\)
5. \(( a b + 5 ) \left( a ^ { 2 } b ^ { 2 } - 5 a b + 25 \right)\)
7. \(\left( 9 x ^ { 2 } + y ^ { 2 } \right) ( 3 x + y ) ( 3 x - y )\)
9. \(( x + 2 y ) \left( x ^ { 2 } - 2 x y + 4 y ^ { 2 } \right) ( x - 2 y ) \left( x ^ { 2 } + 2 x y + 4 y ^ { 2 } \right)\)
Exercise \(\PageIndex{7}\)
Factor.
- \(x ^ { 2 } - 8 x - 48\)
- \(x ^ { 2 } - 15 x + 54\)
- \(x ^ { 2 } - 4 x - 6\)
- \(x ^ { 2 } - 12 x y + 36 y ^ { 2 }\)
- \(x ^ { 2 } + 20 x y + 75 y ^ { 2 }\)
- \(- x ^ { 2 } + 5 x + 150\)
- \(- 2 y ^ { 2 } + 20 y + 48\)
- \(28 x ^ { 2 } + 20 x + 3\)
- \(150 x ^ { 2 } - 100 x + 6\)
- \(24 a ^ { 2 } - 38 a b + 3 b ^ { 2 }\)
- \(27 u ^ { 2 } - 3 u v - 4 v ^ { 2 }\)
- \(16 x ^ { 2 } y ^ { 2 } - 78 x y + 27\)
- \(16 m ^ { 2 } + 72 m n + 81 n ^ { 2 }\)
- \(4 x ^ { 2 } - 5 x + 20\)
- \(25 x ^ { 4 } - 35 x ^ { 2 } + 6\)
- \(2 x ^ { 4 } + 7 x ^ { 2 } + 3\)
- \(x ^ { 6 } + 3 x ^ { 3 } y ^ { 3 } - 10 y ^ { 6 }\)
- \(a ^ { 6 } - 8 a ^ { 3 } b ^ { 3 } + 15 b ^ { 6 }\)
- \(x ^ { 2 n } - 2 x ^ { n } + 1\)
- \(6 x ^ { 2 n } - x ^ { n } - 2\)
- Answer
-
1. \(( x - 12 ) ( x + 4 )\)
3. Prime
5. \(( x + 5 y ) ( x + 15 y )\)
7. \(- 2 ( y - 12 ) ( y + 2 )\)
9. \(2 ( 15 x - 1 ) ( 5 x - 3 )\)
11. \(( 3 u + v ) ( 9 u - 4 v )\)
13. \(( 4 m + 9 n ) ^ { 2 }\)
15. \(\left( 5 x ^ { 2 } - 6 \right) \left( 5 x ^ { 2 } - 1 \right)\)
17. \(\left( x ^ { 3 } + 5 y ^ { 3 } \right) \left( x ^ { 3 } - 2 y ^ { 3 } \right)\)
19. \(\left( x ^ { n } - 1 \right) ^ { 2 }\)
Exercise \(\PageIndex{8}\)
Factor completely.
- \(45 x ^ { 3 } - 20 x\)
- \(12 x ^ { 4 } - 70 x ^ { 3 } + 50 x ^ { 2 }\)
- \(- 20 x ^ { 2 } + 32 x - 3\)
- \(- x ^ { 3 } y + 9 x y ^ { 3 }\)
- \(24 a ^ { 4 } b ^ { 2 } + 3 a b ^ { 5 }\)
- \(64 a ^ { 6 } b ^ { 6 } - 1\)
- \(64 x ^ { 2 } + 1\)
- \(x ^ { 3 } + x ^ { 2 } y - x y ^ { 2 } - y ^ { 3 }\)
- Answer
-
1. \(5 x ( 3 x + 2 ) ( 3 x - 2 )\)
3. \(- ( 10 x - 1 ) ( 2 x - 3 )\)
5. \(3 a b ^ { 2 } ( 2 a + b ) \left( 4 a ^ { 2 } - 2 a b + b ^ { 2 } \right)\)
7. Prime
Exercise \(\PageIndex{9}\)
Solve by factoring.
- \(9 x ^ { 2 } + 8 x = 0\)
- \(x ^ { 2 } - 1 = 0\)
- \(x ^ { 2 } - 12 x + 20 = 0\)
- \(x ^ { 2 } - 2 x - 48 = 0\)
- \(( 2 x + 1 ) ( x - 2 ) = 3\)
- \(2 - ( x - 4 ) ^ { 2 } = - 7\)
- \(( x - 6 ) ( x + 3 ) = - 18\)
- \(( x + 5 ) ( 2 x - 1 ) = 3 ( 2 x - 1 )\)
- \(\frac { 1 } { 2 } x ^ { 2 } + \frac { 2 } { 3 } x - \frac { 1 } { 8 } = 0\)
- \(\frac { 1 } { 4 } x ^ { 2 } - \frac { 19 } { 12 } x + \frac { 1 } { 2 } = 0\)
- \(x ^ { 3 } - 2 x ^ { 2 } - 24 x = 0\)
- \(x ^ { 4 } - 5 x ^ { 2 } + 4 = 0\)
- Answer
-
1. \(-\frac{8}{9} , 0\)
3. \(2,10\)
5. \(-1, \frac{5}{2}\)
7. \(0,3\)
9. \(- \frac { 3 } { 2 } , \frac { 1 } { 6 }\)
11. \(- 4,0,6\)
Exercise \(\PageIndex{10}\)
Find the roots of the given functions.
- \(f ( x ) = 12 x ^ { 2 } - 8 x\)
- \(g ( x ) = 2 x ^ { 3 } - 18 x\)
- \(h ( t ) = - 16 t ^ { 2 } + 64\)
- \(p ( x ) = 5 x ^ { 2 } - 21 x + 4\)
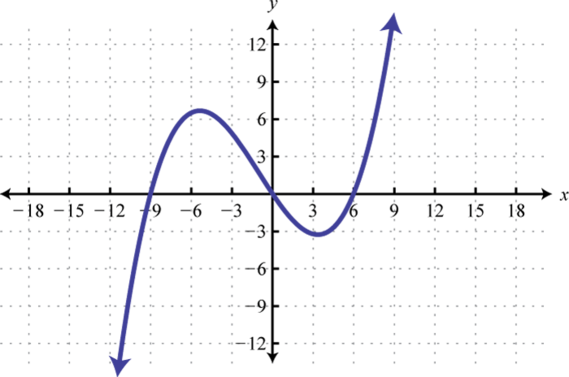
6.
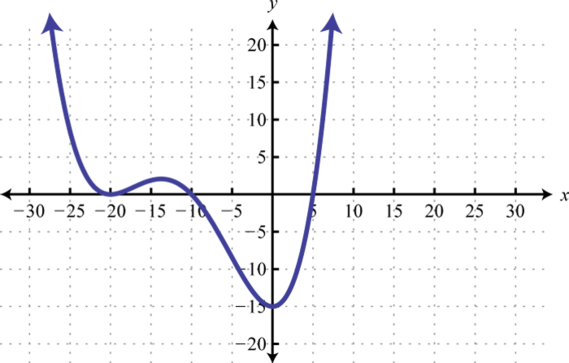
7. The height in feet of an object dropped from the top of a \(16\)-foot ladder is given by \(h ( t ) = - 16 t ^ { 2 } + 16\), where \(t\) represents the time in seconds after the object has been dropped. How long will it take to hit the ground?
8. The length of a rectangle is \(2\) centimeters less than twice its width. If the area of the rectangle is \(112\) square centimeters, find its dimensions.
9. A triangle whose base is equal in measure to its height has an area of \(72\) square inches. Find the length of the base.
10. A box can be made by cutting out the corners and folding up the edges of a sheet of cardboard. A template for a rectangular cardboard box of height \(2\) inches is given.
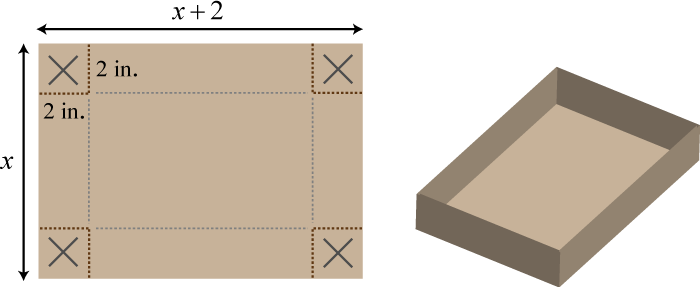
What are the dimensions of a cardboard sheet that will make a rectangular box with volume \(240\) cubic inches?
- Answer
-
1. \(0 , \frac { 2 } { 3 }\)
3. \(\pm 2\)
5. \(- 9,0,6\)
7. \(1\) second
9. \(12\) inches
Exercise \(\PageIndex{11}\)
Solve or factor.
- \(x ^ { 2 } - 25\)
- \(x ^ { 2 } - 121 = 0\)
- \(16 x ^ { 2 } - 22 x - 3 = 0\)
- \(3 x ^ { 2 } - 14 x - 5\)
- \(x ^ { 3 } - x ^ { 2 } - 2 x - 2\)
- \(3 x ^ { 2 } = - 15 x\)
- Answer
-
1. Factor; \(( x + 5 ) ( x - 5 )\)
3. Solve; \(- \frac { 1 } { 8 } , \frac { 3 } { 2 }\)
5. Factor; \(( x - 1 ) \left( x ^ { 2 } - 2 \right)\)
Exercise \(\PageIndex{12}\)
Find a polynomial equation with integer coefficients, given the solutions.
- \(5, -2\)
- \(\frac { 2 } { 3 } , - \frac { 1 } { 2 }\)
- \(\pm \frac { 4 } { 5 }\)
- \(\pm 10\)
- \(-4,0,3\)
- \(-8\) double root
- Answer
-
1. \(x ^ { 2 } - 3 x - 10 = 0\)
3. \(25 x ^ { 2 } - 16 = 0\)
5. \(x ^ { 3 } + x ^ { 2 } - 12 x = 0\)
Exercise \(\PageIndex{13}\)
State the restrictions and simplify.
- \(\frac { 108 x ^ { 3 } } { 12 x ^ { 2 } }\)
- \(\frac { 56 x ^ { 2 } ( x - 2 ) ^ { 2 } } { 8 x ( x - 2 ) ^ { 3 } }\)
- \(\frac { 64 - x ^ { 2 } } { 2 x ^ { 2 } - 15 x - 8 }\)
- \(\frac { 3 x ^ { 2 } + 28 x + 9 } { 81 - x ^ { 2 } }\)
- \(\frac { x ^ { 2 } - 25 } { 5 x ^ { 2 } } \cdot \frac { 10 x ^ { 2 } - 15 x } { 2 x ^ { 2 } + 7 x - 15 }\)
- \(\frac { 7 x ^ { 2 } - 41 x - 6 } { ( x - 7 ) ^ { 2 } } \cdot \frac { 49 - x ^ { 2 } } { x ^ { 2 } + x - 42 }\)
- \(\frac { 28 x ^ { 2 } ( 2 x - 3 ) } { 4 x ^ { 2 } - 9 } \div \frac { 7 x } { 4 x ^ { 2 } - 12 x + 9 }\)
- \(\frac { x ^ { 2 } - 10 x + 24 } { x ^ { 2 } - 8 x + 16 } \div \frac { 2 x ^ { 2 } - 13 x + 6 } { x ^ { 2 } + 2 x - 24 }\)
- Answer
-
1. \(9 x ; x \neq 0\)
3. \(- \frac { x + 8 } { 2 x + 1 } ; x \neq - \frac { 1 } { 2 } , 8\)
5. \(\frac { x - 5 } { x } ; x \neq - 5,0 , \frac { 3 } { 2 }\)
7. \(\frac { 4 x ( 2 x - 3 ) ^ { 2 } } { 2 x + 3 } ; x \neq \pm \frac { 3 } { 2 } , 0\)
Exercise \(\PageIndex{14}\)
Perform the operations and simplify. Assume all variable expressions in the denominator are nonzero.
- \(\frac { a ^ { 2 } - b ^ { 2 } } { 4 a ^ { 2 } b ^ { 2 } + 4 a b ^ { 3 } } \cdot \frac { 2 a b } { a ^ { 2 } - 2 a b + b ^ { 2 } }\)
- \(\frac { a ^ { 2 } - 5 a b + 6 b ^ { 2 } } { a ^ { 2 } - 4 a b + 4 b ^ { 2 } } \div \frac { 9 b ^ { 2 } - a ^ { 2 } } { 3 a ^ { 3 } b - 6 a ^ { 2 } b ^ { 2 } }\)
- \(\frac { x ^ { 2 } + x y + y ^ { 2 } } { 4 x ^ { 2 } + 3 x y - y ^ { 2 } } \cdot \frac { x ^ { 2 } - y ^ { 2 } } { x ^ { 3 } - y ^ { 3 } } \div \frac { x + y } { 12 x ^ { 2 } y - 3 x y ^ { 2 } }\)
- \(\frac { x ^ { 4 } - y ^ { 4 } } { x ^ { 2 } - 2 x y + y ^ { 2 } } \div \frac { x ^ { 2 } - 4 x y - 5 y ^ { 2 } } { 10 x ^ { 3 } } \cdot \frac { 2 x ^ { 2 } - 11 x y + 5 y ^ { 2 } } { 2 x ^ { 3 } y + 2 x y ^ { 3 } }\)
- Answer
-
1. \(\frac { 1 } { 2 b ( a - b ) }\)
3. \(\frac { 3 x y } { x + y }\)
Exercise \(\PageIndex{15}\)
Perform the operations and state the restrictions.
- Given \(f ( x ) = \frac { 4 x ^ { 2 } + 39 x - 10 } { x ^ { 2 } + 3 x - 10 }\) and \(g ( x ) = \frac { 2 x ^ { 2 } + 7 x - 15 } { x ^ { 2 } + 13 x + 30 }\), find \(( f \cdot g ) ( x )\).
- Given \(f ( x ) = \frac { 25 - x ^ { 2 } } { 3 + x }\) and \(g ( x ) = \frac { 9 - x ^ { 2 } } { 5 - x }\), find \(( f \cdot g ) ( x )\).
- Given \(f ( x ) = \frac { 42 x ^ { 2 } } { 2 x ^ { 2 } + 3 x - 2 }\) and \(g ( x ) = \frac { 14 x } { 4 x ^ { 2 } - 4 x + 1 }\), find \(( f / g ) ( x )\).
- Given \(f ( x ) = \frac { x ^ { 2 } - 20 x + 100 } { x ^ { 2 } - 1 }\) and \(g ( x ) = \frac { x ^ { 2 } - 100 } { x ^ { 2 } + 2 x + 1 }\), find \(( f / g ) ( x )\).
- The daily cost in dollars of running a small business is given by \(C (x) = 150 + 45x\) where \(x\) represents the number of hours the business is in operation. Determine the average cost per hour if the business is in operation for \(8\) hours in a day.
- An electric bicycle manufacturer has determined that the cost of producing its product in dollars is given by the function \(C (n) = 2n^{2} + 100n + 2,500\) where \(n\) represents the number of electric bicycles produced in a day. Determine the average cost per bicycle if \(10\) and \(20\) are produced in a day.
- Given \(f ( x ) = 3 x - 5\), simplify \(\frac { f ( x + h ) - f ( x ) } { h }\).
- Given \(g ( x ) = 2 x ^ { 2 } - x + 1\), simplify \(\frac { g ( x + h ) - g ( x ) } { h }\).
- Answer
-
1. \(( f \cdot g ) ( x ) = \frac { ( 4 x - 1 ) ( 2 x - 3 ) } { ( x - 2 ) ( x + 3 ) } ; x \neq - 10 , - 5 , - 3,2\)
3. \(( f / g ) ( x ) = \frac { 3 x ( 2 x - 1 ) } { x + 2 } ; x \neq - 2,0 , \frac { 1 } { 2 }\)
5. \(\$ 63.75\) per hour
7. \(3\)
Exercise \(\PageIndex{16}\)
State the restrictions and simplify.
- \(\frac { 5 x - 6 } { x ^ { 2 } - 36 } - \frac { 4 x } { x ^ { 2 } - 36 }\)
- \(\frac { 2 } { x } + 5 x\)
- \(\frac { 5 } { x - 5 } + \frac { 1 } { 2 x }\)
- \(\frac { x } { x - 2 } + \frac { 3 } { x + 3 }\)
- \(\frac { 7 ( x - 1 ) } { 4 x ^ { 2 } - 17 x + 15 } - \frac { 2 } { x - 3 }\)
- \(\frac { 5 } { x } - \frac { 19 x + 25 } { 2 x ^ { 2 } + 5 x }\)
- \(\frac { x } { x - 5 } - \frac { 2 } { x - 3 } - \frac { 5 ( x - 3 ) } { x ^ { 2 } - 8 x + 15 }\)
- \(\frac { 3 x } { 2 x - 1 } - \frac { x - 4 } { x + 4 } + \frac { 12 ( 2 - x ) } { 2 x ^ { 2 } + 7 x - 4 }\)
- \(\frac { 1 } { t - 1 } + \frac { 1 } { ( t - 1 ) ^ { 2 } } - \frac { 1 } { t ^ { 2 } - 1 }\)
- \(\frac { 1 } { t - 1 } - \frac { 2 t - 5 } { t ^ { 2 } - 2 t + 1 } - \frac { 5 t ^ { 2 } - 3 t - 2 } { ( t - 1 ) ^ { 3 } }\)
- \(2 x ^ { - 1 } + x ^ { - 2 }\)
- \(( x - 4 ) ^ { - 1 } - 2 x ^ { - 2 }\)
- Answer
-
1. \(\frac { 1 } { x + 6 } ; x \neq \pm 6\)
3. \(\frac { 11 x - 5 } { 2 x ( x - 5 ) } ; x \neq 0,5\)
5. \(- \frac { 1 } { 4 x - 5 } ; x \neq \frac { 5 } { 4 } , 3\)
7. \(\frac { x - 5 } { x - 3 } ; x \neq 3,5\)
9. \(\frac { t ^ { 2 } + 1 } { ( t + 1 ) ( t - 1 ) ^ { 2 } } ; t \neq \pm 1\)
11. \(\frac { 2 x + 1 } { x ^ { 2 } } ; x \neq 0\)
Exercise \(\PageIndex{17}\)
Simplify. Assume that all variable expressions used as denominators are nonzero.
- \(\frac { \frac { 1 } { 7 } + \frac { 1 } { x } } { \frac { 1 } { 49 } - \frac { 1 } { x ^ { 2 } } }\)
- \(\frac { \frac { 1 } { 100 } - \frac { 1 } { x ^ { 2 } } } { \frac { 1 } { x } - \frac { 1 } { 10 } }\)
- \(\frac { \frac { 3 } { x } - \frac { 1 } { x - 5 } } { \frac { 5 } { x + 2 } - \frac { 2 } { x } }\)
- \(\frac { 1 - \frac { 12 } { x } + \frac { 35 } { x ^ { 2 } } } { 1 - \frac { 25 } { x ^ { 2 } } }\)
- \(\frac { x - 4 x ^ { - 1 } } { 2 - 5 x ^ { - 1 } + 2 x ^ { - 2 } }\)
- \(\frac { 8 x ^ { - 1 } + y ^ { - 1 } } { y ^ { - 2 } - 64 x ^ { - 2 } }\)
- Answer
-
1. \(\frac { 7 x } { x - 7 }\)
3. \(\frac { ( x + 2 ) ( 2 x - 15 ) } { ( x - 5 ) ( 3 x - 4 ) }\)
5. \(\frac { x ( x + 2 ) } { 2 x - 1 }\)
Exercise \(\PageIndex{18}\)
Perform the operations and state the restrictions.
- Given \(f ( x ) = \frac { 3 } { x - 3 }\) and \(g ( x ) = \frac { x - 2 } { x + 2 }\), find \(( f + g ) ( x )\).
- Given \(f ( x ) = \frac { 1 } { x ^ { 2 } + x }\) and \(g ( x ) = \frac { 2 x } { x ^ { 2 } - 1 }\), find \(( f + g ) ( x )\).
- Given \(f ( x ) = \frac { x - 3 } { x - 5 }\) and \(g ( x ) = \frac { x ^ { 2 } - x } { x ^ { 2 } - 25 }\), find \(( f - g ) ( x )\).
- Given \(f ( x ) = \frac { 11 x + 4 } { x ^ { 2 } - 2 x - 8 }\) and \(g ( x ) = \frac { 2 x } { x - 4 }\), find \(( f - g ) ( x )\).
- Answer
-
1. \(( f + g ) ( x ) = \frac { x ^ { 2 } - 2 x + 12 } { ( x - 3 ) ( x + 2 ) } ; x \neq - 2,3\)
3. \(( f - g ) ( x ) = \frac { 3 } { x + 5 } ; x \neq \pm 5\)
Exercise \(\PageIndex{19}\)
Solve.
- \(\frac { 3 } { x } = \frac { 1 } { 2 x + 15 }\)
- \(\frac { x } { x - 4 } = \frac { x + 8 } { x - 8 }\)
- \(\frac { x + 5 } { 2 ( x + 2 ) } + \frac { x - 2 } { x + 4 } = 1\)
- \(\frac { 2 x } { x - 5 } + \frac { 1 } { x + 1 } = 0\)
- \(\frac { x + 1 } { x - 4 } + \frac { 4 } { x + 6 } = - \frac { 10 } { x ^ { 2 } + 2 x - 24 }\)
- \(\frac { 2 } { x } - \frac { 12 } { 2 x + 3 } = \frac { 2 - 3 x ^ { 2 } } { 2 x ^ { 2 } + 3 x }\)
- \(\frac { x + 7 } { x - 2 } - \frac { 9 } { x + 7 } = \frac { 81 } { x ^ { 2 } + 5 x - 14 }\)
- \(\frac { x } { x + 5 } + \frac { 1 } { x - 4 } = \frac { 4 x - 7 } { x ^ { 2 } + x - 20 }\)
- \(\frac { 2 } { 3 x - 1 } + \frac { x } { 2 x + 1 } = \frac { 2 ( 3 - 4 x ) } { 6 x ^ { 2 } + x - 1 }\)
- \(\frac { x } { x - 1 } + \frac { 1 } { x + 1 } = \frac { 2 x } { x ^ { 2 } - 1 }\)
- \(\frac { 2 x } { x + 5 } - \frac { 1 } { 2 x - 3 } = \frac { 4 - 7 x } { 2 x ^ { 2 } + 7 x - 15 }\)
- \(\frac { x } { x + 4 } + \frac { 1 } { 2 x + 7 } = \frac { x + 8 } { 2 x ^ { 2 } + 15 x + 28 }\)
- \(\frac { 1 } { t - 1 } - \frac { 2 } { 2 t + 1 } = \frac { 1 } { t - 2 } - \frac { 2 } { 2 t - 1 }\)
- \(\frac { t - 1 } { t - 2 } - \frac { t - 2 } { t - 3 } = \frac { t - 3 } { t - 4 } - \frac { t - 4 } { t - 5 }\)
- Solve for \(a\) : \(\frac { 1 } { a } = \frac { 1 } { b } - \frac { 1 } { c }\)
- Solve for \(y\) : \(x = \frac { 3 y - 1 } { y - 5 }\)
- A positive integer is \(4\) less than another. If the reciprocal of the larger integer is subtracted from twice the reciprocal of the smaller, the result is \(\frac{1}{6}\). Find the two integers.
- If \(3\) times the reciprocal of the larger of two consecutive odd integers is added to \(7\) times the reciprocal of the smaller, the result is \(\frac{4}{3}\). Find the integers.
- If the reciprocal of the smaller of two consecutive integers is subtracted from three times the reciprocal of the larger, the result is \(\frac{3}{10}\). Find the integers.
- A positive integer is twice that of another. The sum of the reciprocals of the two positive integers is \(\frac{1}{4}\). Find the two integers.
- Answer
-
1. \(−9\)
3. \(−1, 4\)
5. \(−11, 0\)
7. \(Ø\)
9. \(−4\)
11. \(−\frac{3 }{2}\)
13. \(\frac{3}{4}\)
15. \(a = \frac { b c } { c - b }\)
17. \({8, 12}\)
19. \({5, 6}\)
Exercise \(\PageIndex{20}\)
Use algebra to solve the following applications.
- Manuel traveled \(8\) miles on the bus and another \(84\) miles on a train. If the train was \(16\) miles per hour faster than the bus, and the total trip took \(2\) hours, what was the average speed of the train?
- A boat can average \(10\) miles per hour in still water. On a trip downriver, the boat was able to travel \(7.5\) miles with the current. On the return trip, the boat was only able to travel \(4.5\) miles in the same amount of time against the current. What was the speed of the current?
- Susan can jog, on average, \(1 \frac{1}{2}\) miles per hour faster than her husband Bill. Bill can jog \(10\) miles in the same amount of time it takes Susan to jog \(13\) miles. How fast, on average, can Susan jog?
- In the morning, Raul drove \(8\) miles to visit his grandmother and then returned later that evening. Because of traffic, his average speed on the return trip was \(\frac{1}{2}\) that of his average speed that morning. If the total driving time was \(\frac{3}{4}\) of an hour, what was his average speed on the return trip?
- One pipe can completely fill a water tank in \(6\) hours while another smaller pipe takes \(8\) hours to fill the same tank. How long will it take to fill the tank to \(\frac{3}{4}\) capacity if both pipes are turned on?
- It takes Bill \(3\) minutes longer than Jerry to fill an order. Working together they can fill \(15\) orders in \(30\) minutes. How long does it take Bill to fill an order by himself?
- Manny takes twice as long as John to assemble a skateboard. If they work together, they can assemble a skateboard in \(6\) minutes. How long would it take Manny to assemble the skateboard without John’s help?
- Working alone, Joe can complete the yard work in \(30\) minutes. It takes Mike \(45\) minutes to complete work on the same yard. How long would it take them working together?
- Answer
-
1. \(48\) miles per hour
3. \(6.5\) miles per hour
5. Approximately \(2.6\) hours
7. \(18\) minutes
Exercise \(\PageIndex{21}\)
Construct a mathematical model given the following:
- \(y\) varies directly as \(x\), where \(y=30\) when \(x=5\).
- \(y\) varies inversely as \(x\), where \(y=3\) when \(x=-2\).
- \(y\) is jointly proportional to \(x\) and \(z\), where \(y=-50\) when \(x=-2\) and \(z=5\).
- \(y\) is directly proportional to the square of \(x\) and inversely proportional to \(z\), where \(y=-6\) when \(x=2\) and \(z=-8\).
- The distance an object in free fall varies directly with the square of the time that it has been falling. It is observed that an object falls \(36\) feet in \(1 \frac{1}{2}\) seconds. Find an equation that models the distance an object will fall, and use it to determine how far it will fall in \(2 \frac{1}{2}\) seconds.
- After the brakes are applied, the stopping distance \(d\) of an automobile varies directly with the square of the speed \(s\) of the car. If a car traveling \(55\) miles per hour takes \(181.5\) feet to stop, how many feet will it take to stop if it is moving \(65\) miles per hour?
- The weight of an object varies inversely as the square of its distance from the center of the Earth. If an object weighs \(180\) lbs on the surface of the Earth (approximately \(4,000\) miles from the center), then how much will it weigh at \(2,000\) miles above the Earth’s surface?
- The cost per person of renting a limousine varies inversely with the number of people renting it. If \(5\) people go in on the rental, the limousine will cost \($112\) per person. How much will the rental cost per person if \(8\) people go in on the rental?
- To balance a seesaw, the distance from the fulcrum that a person must sit is inversely proportional to his weight. If a \(52\)-pound boy is sitting \(3\) feet away from the fulcrum, then how far from the fulcrum must a \(44\)-pound boy sit? Round to the nearest tenth of a foot.
- Answer
-
1. \(y=6x\)
3. \(y=5xz\)
5. \(d=16t^{2}\); \(100\) feet
7. \(80\) lbs
9. Approximately \(3.5\) feet
Sample Exam
Exercise \(\PageIndex{22}\)
Given \(f ( x ) = x ^ { 2 } - x + 4 , g ( x ) = 5 x - 1\), and \(h ( x ) = 2 x ^ { 2 } + x - 3\), find the following:
- \(( g \cdot h ) ( x )\)
- \(( h - f ) ( x )\)
- \(( f + g ) ( - 1 )\)
- Answer
-
1. \(( g \cdot h ) ( x ) = 10 x ^ { 3 } + 3 x ^ { 2 } - 16 x + 3\)
3. \(( f + g ) ( - 1 ) = 0\)
Exercise \(\PageIndex{23}\)
Factor.
- \(x ^ { 3 } + 16 x - 2 x ^ { 2 } - 32\)
- \(x ^ { 3 } - 8 y ^ { 3 }\)
- \(x ^ { 4 } - 81\)
- \(25 x ^ { 2 } y ^ { 2 } - 40 x y + 16\)
- \(16 x ^ { 3 } y + 12 x ^ { 2 } y ^ { 2 } - 18 x y ^ { 3 }\)
- Answer
-
2. \(( x - 2 y ) \left( x ^ { 2 } + 2 x y + 4 y ^ { 2 } \right)\)
4. \(( 5 x y - 4 ) ^ { 2 }\)
Exercise \(\PageIndex{24}\)
Solve
- \(6 x ^ { 2 } + 24 x = 0\)
- \(( 2 x + 1 ) ( 3 x + 2 ) = 12\)
- \(( 2 x + 1 ) ^ { 2 } = 23 x + 6\)
- Find a quadratic equation with integer coefficients given the solutions \(\left\{ \frac { 1 } { 2 } , - 3 \right\}\).
- Given \(f ( x ) = 5 x ^ { 2 } - x + 4\), simplify \(\frac { f ( x + h ) - f ( x ) } { h }\), where \(h \neq 0\).
- Answer
-
1. \(-4,0\)
3. \(-\frac{1}{4}, 5\)
5. \(10x+5h-1\)
Exercise \(\PageIndex{25}\)
Simplify and state the restrictions.
- \(\frac { 4 x ^ { 2 } - 33 x + 8 } { x ^ { 2 } - 10 x + 16 } \div \frac { 16 x ^ { 2 } - 1 } { x ^ { 2 } - 4 x + 4 }\)
- \(\frac { x - 1 } { x - 7 } + \frac { 1 } { 1 - x } - \frac { 2 ( x + 11 ) } { x ^ { 2 } - 8 x + 7 }\)
- Answer
-
2. \(\frac { x + 2 } { x - 1 } ; x \neq 1,7\)
Exercise \(\PageIndex{26}\)
Assume all variable expressions in the denominator are nonzero and simplify.
- \(\frac { \frac { 3 } { x } + \frac { 1 } { y } } { \frac { 1 } { y ^ { 2 } } - \frac { 9 } { x ^ { 2 } } }\)
Exercise \(\PageIndex{27}\)
Solve.
- \(\frac { 6 x - 5 } { 3 x + 2 } = \frac { 2 x } { x + 1 }\)
- \(\frac { 2 x } { x + 5 } - \frac { 1 } { 5 - x } = \frac { 2 x } { x ^ { 2 } - 25 }\)
- Find the root of the function defined by \(f ( x ) = \frac { 1 } { x + 3 } - 4\).
- Solve for \(y\): \(x = \frac { 4 y } { 3 y - 1 }\)
- Answer
-
1. \(-\frac{5}{3}\)
3. \(-\frac{11}{4}\)
Exercise \(\PageIndex{28}\)
Use algebra to solve.
- The height of an object dropped from a \(64\)-foot building is given by the function \(h (t) = −16t^{2} + 64\), where \(t\) represents time in seconds after it was dropped.
- Determine the height of the object at \(\frac{3}{4}\) of a second.
- How long will it take the object to hit the ground?
- One positive integer is \(3\) units more than another. When the reciprocal of the larger is subtracted from twice the reciprocal of the smaller, the result is \(\frac{2}{9}\). Find the two positive integers.
- A light airplane can average \(126\) miles per hour in still air. On a trip, the airplane traveled \(222\) miles with a tailwind. On the return trip, against a headwind of the same speed, the plane was only able to travel \(156\) miles in the same amount of time. What was the speed of the wind?
- On the production line, it takes John \(2\) minutes less time than Mark to assemble a watch. Working together they can assemble \(5\) watches in \(12\) minutes. How long does it take John to assemble a watch working alone?
- Write an equation that relates \(x\) and \(y\), given that \(y\) varies inversely with the square of \(x\), where \(y = −\frac{1}{3}\) when \(x = 3\). Use it to find \(y\) when \(x = \frac{1}{2}\).
- Answer
-
1. (1) \(55\) feet; (2) \(2\) seconds
3. \(22\) miles per hour
5. \(y = - \frac { 3 } { x ^ { 2 } } ; y = - 12\)


