7.E: Exponential and Logarithmic Functions (Exercises)
- Page ID
- 6440
Exercise \(\PageIndex{1}\)
Given \(f\) and \(g\) find \((f \circ g)(x)\) and \((g \circ f)(x)\).
- \(f(x)=6 x-5, g(x)=2 x+1\)
- \(f(x)=5-6 x, g(x)=\frac{3}{2} x\)
- \(f(x)=2 x^{2}+x-2, g(x)=5 x\)
- \(f(x)=x^{2}-x-6, g(x)=x-3\)
- \(f(x)=\sqrt{x+2}, g(x)=8 x-2\)
- \(f(x)=\frac{x-1}{3 x-1}, g(x)=\frac{1}{x}\)
- \(f(x)=x^{2}+3 x-1, g(x)=\frac{1}{x-2}\)
- \(f(x)=\sqrt[3]{3(x+2)}, g(x)=9 x^{3}-2\)
- Answer
-
1. \((f \circ g)(x)=12 x+1 ;(g \circ f)(x)=12 x-9\)
3. \(\begin{array}{l}{(f \circ g)(x)=50 x^{2}+5 x-2}; \: {(g \circ f)(x)=10 x^{2}+5 x-10}\end{array}\)
5. \((f\circ g)(x)=2\sqrt{2x};\:(g\circ f)(x)=8\sqrt{x+2}-2\)
7. \(\begin{array}{c}{(f \circ g)(x)=-\frac{x^{2}-7 x+9}{(x-2)^{2}}}; \: {\left(g \circ f\right)(x)=\frac{1}{x^{2}+3 x-3}}\end{array}\)
Exercise \(\PageIndex{1}\)
Are the given functions one-to-one? Explain.
1.
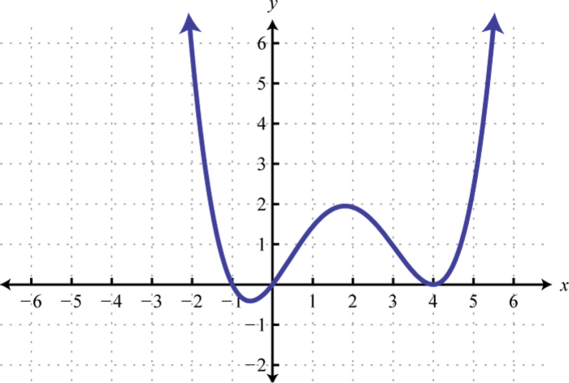
Figure 7.E.1
2.
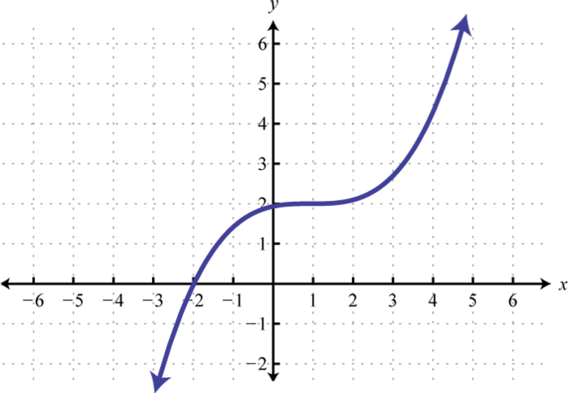
Figure 7.E.2
3.
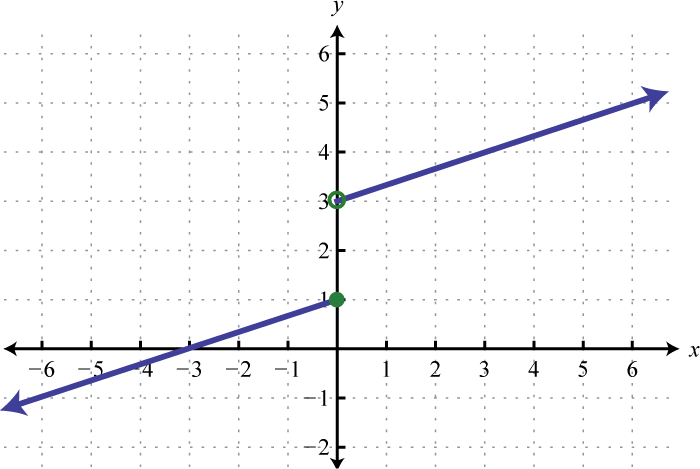
Figure 7.E.3
4.
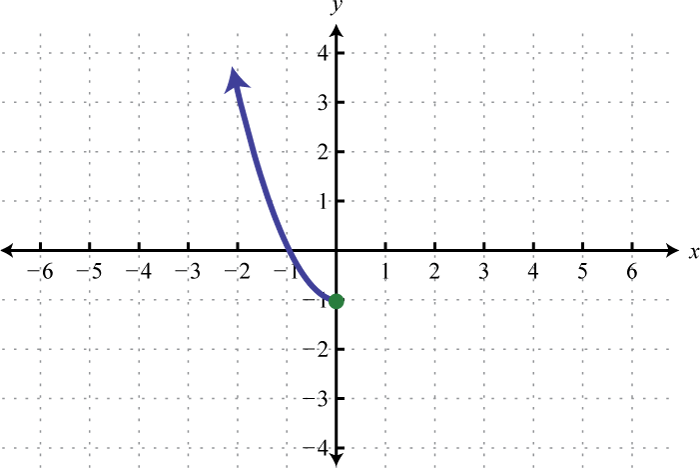
Figure 7.E.4
- Answer
-
1. No, fails the HLT
3. Yes, passes the HLT
Exercise \(\PageIndex{3}\)
Verify algebraically that the two given functions are inverses. In other words, show that \(\left(f \circ f^{-1}\right)(x)=x\) and \(\left(f^{-1} \circ f\right)(x)=x\).
- \(f(x)=6 x-5, f^{-1}(x)=\frac{1}{6} x+\frac{5}{6}\)
- \(f(x)=\sqrt{2 x+3}, f^{-1}(x)=\frac{x^{2}-3}{2}, x \geq 0\)
- \(f(x)=\frac{x}{3 x-2}, f^{-1}(x)=\frac{2 x}{3 x-1}\)
- \(f(x)=\sqrt[3]{x+3}-4, f^{-1}(x)=(x+4)^{3}-3\)
- Answer
-
1. Proof
3. Proof
Exercise \(\PageIndex{4}\)
Find the inverses of each function defined as follows:
- \(f(x)=-7 x+3\)
- \(f(x)=\frac{2}{3} x-\frac{1}{2}\)
- \(g(x)=x^{2}-12, x \geq 0\)
- \(g(x)=(x-1)^{3}+5\)
- \(g(x)=\frac{2}{x-1}\)
- \(h(x)=\frac{x+5}{x-5}\)
- \(h(x)=\frac{3 x-1}{x}\)
- \(p(x)=\sqrt[3]{5 x}+3\)
- \(h(x)=\sqrt[3]{2 x-7}+2\)
- \(h(x)=\sqrt[5]{x+2}-3\)
- Answer
-
1. \(f^{-1}(x)=-\frac{1}{7} x+\frac{3}{7}\)
3. \(g^{-1}(x)=\sqrt{x+12}\)
5. \(g^{-1}(x)=\frac{x+2}{x}\)
7. \(h^{-1}(x)=-\frac{1}{x-3}\)
9. \(h^{-1}(x)=\frac{(x-2)^{3}+7}{2}\)
Exercise \(\PageIndex{5}\)
Evaluate.
- \(f(x)=5^{x} ;\) find \(f(-1), f(0),\) and \(f(3).\)
- \(f(x)=\left(\frac{1}{2}\right)^{x} ;\) find \(f(-4), f(0),\) and \(f(-3).\)
- \(g(x)=10^{-x} ;\) find \(g(-5), g(0),\) and \(g(2).\)
- \(g(x)=1-3^{x} ;\) find \(g(-2), g(0),\) and \(g(3).\)
- Answer
-
1. \(f(-1)=\frac{1}{5}, f(0)=1, f(3)=125\)
3. \(g(-5)=100,000, g(0)=1, g(2)=\frac{1}{100}\)
Exercise \(\PageIndex{6}\)
Sketch the exponential function. Draw the horizontal asymptote with a dashed line.
- \(f(x)=5^{x}+10\)
- \(f(x)=5^{x-4}\)
- \(f(x)=-3^{x}-9\)
- \(f(x)=3^{x+2}+6\)
- \(f(x)=\left(\frac{1}{3}\right)^{x}\)
- \(f(x)=\left(\frac{1}{2}\right)^{x}-4\)
- \(f(x)=2^{-x}+3\)
- \(f(x)=1-3^{-x}\)
- Answer
-
1.
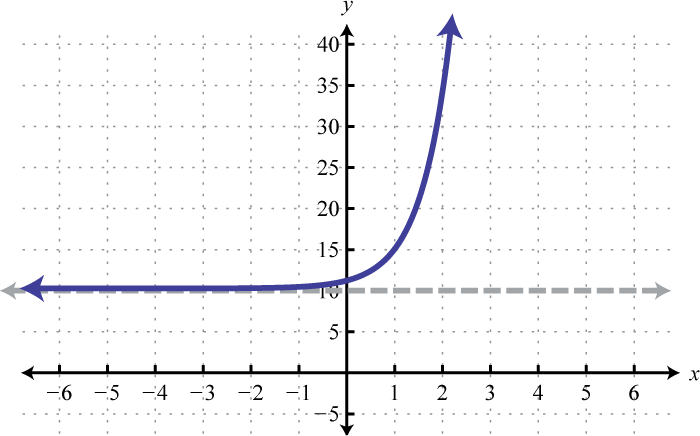
Figure 7.E.5
3.
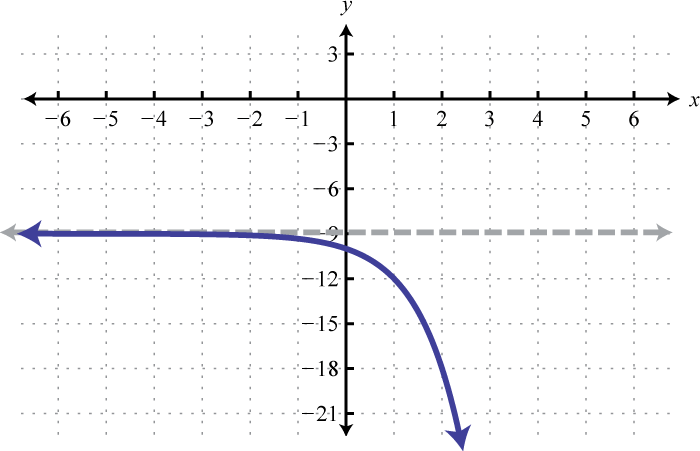
Figure 7.E.6
5.
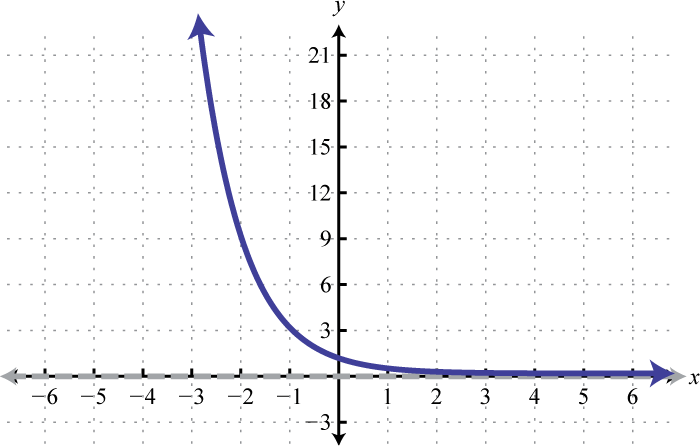
Figure 7.E.7
7.
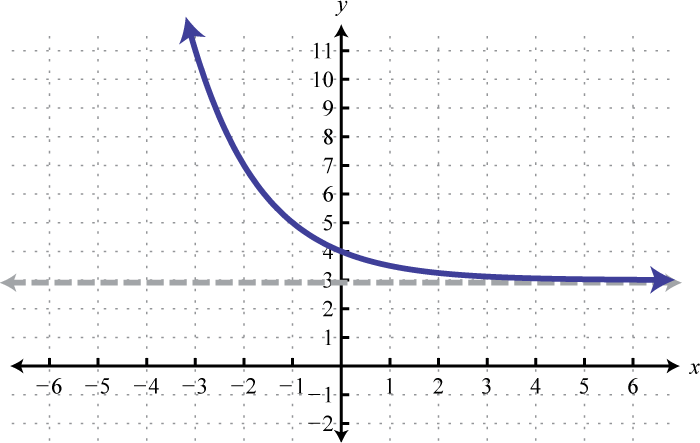
Figure 7.E.8
Exercise \(\PageIndex{7}\)
Use a calculator to evaluate the following. Round off to the nearest hundredth.
- \(f(x)=e^{x}+1 ;\) find \(f(-3), f(-1),\) and \(f\left(\frac{1}{2}\right)\).
- \(g(x)=2-3 e^{x} ;\) find \(g(-1), g(0),\) and \(g\left(\frac{2}{3}\right)\).
- \(p(x)=1-5 e^{-x} ;\) find \(p(-4), p\left(-\frac{1}{2}\right),\) and \(p(0)\).
- \(r(x)=e^{-2 x}-1 ;\) find \(r(-1), r\left(\frac{1}{4}\right),\) and \(r(2)\).
- Answer
-
1. \(f(-3) \approx 1.05, f(-1) \approx 1.37, f\left(\frac{1}{2}\right) \approx 2.65\)
3. \(p(-4) \approx-271.99, p\left(-\frac{1}{2}\right) \approx-7.24, p(0)=-4\)
Exercise \(\PageIndex{8}\)
Sketch the function. Draw the horizontal asymptote with a dashed line.
- \(f(x)=e^{x}+4\)
- \(f(x)=e^{x-4}\)
- \(f(x)=e^{x+3}+2\)
- \(f(x)=e^{-x}+5\)
- Jerry invested $\(6,250\) in an account earning \(3 \frac{5}{8}\)% annual interest that is compounded monthly. How much will be in the account after \(4\) years?
- Jose invested $\(7,500\) in an account earning \(4 \frac{1}{4}\)% annual interest that is compounded continuously. How much will be in the account after \(3 \frac{1}{2}\) years?
- A \(14\)-gram sample of radioactive iodine is accidently released into the atmosphere. The amount of the substance in grams is given by the formula \(P (t) = 14e^{ −0.087t}\), where \(t\) represents the time in days after the sample was released. How much radioactive iodine will be present in the atmosphere \(30\) days after it was released?
- The number of cells in a bacteria sample is given by the formula \(N(t)=\frac{2.4 \times 10^{5}}{1+9 e^{-0.28t}}\), where \(t\) represents the time in hours since the initial placement of \(24,000\) cells. Use the formula to calculate the number of cells in the sample \(20\) hours later.
- Answer
-
1.
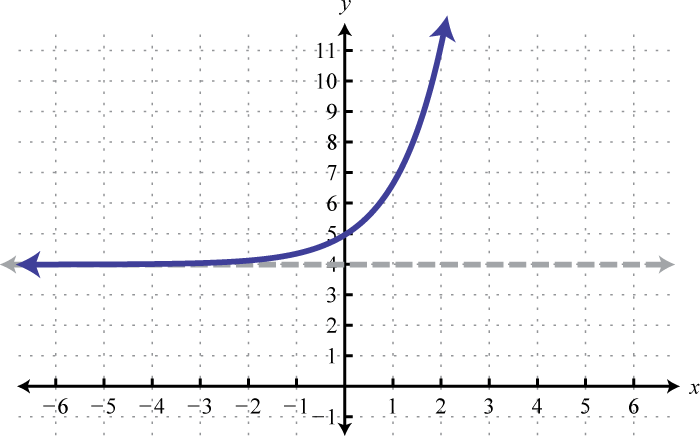
Figure 7.E.9
3.
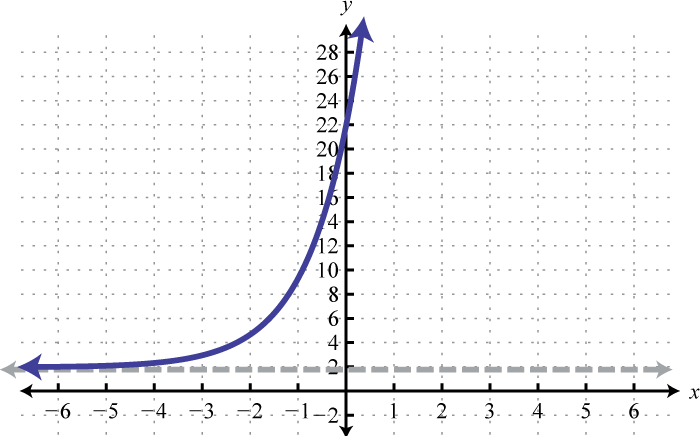
Figure 7.E.10
5. $\(7,223.67\)
7. Approximately \(1\) gram
Exercise \(\PageIndex{9}\)
Evaluate.
- \(\log _{4} 16\)
- \(\log _{3} 27\)
- \(\log _{2}\left(\frac{1}{32}\right)\)
- \(\log \left(\frac{1}{10}\right)\)
- \(\log _{1 / 3} 9\)
- \(\log _{3 / 4}\left(\frac{4}{3}\right)\)
- \(\log _{7} 1\)
- \(\log _{3}(-3)\)
- \(\log _{4} 0\)
- \(\log _{3} 81\)
- \(\log _{6} \sqrt{6}\)
- \(\log _{5} \sqrt[3]{25}\)
- \(\ln e^{8}\)
- \(\ln \left(\frac{1}{e^{5}}\right)\)
- \(\log (0.00001)\)
- \(\log 1,000,000\)
- Answer
-
1. \(2\)
3. \(−5\)
5. \(−2\)
7. \(0\)
9. Undefined
11. \(\frac{1}{2}\)
13. \(8\)
15. \(−5\)
Exercise \(\PageIndex{10}\)
Find \(x\).
- \(\log _{5} x=3\)
- \(\log _{3} x=-4\)
- \(\log _{2 / 3} x=3\)
- \(\log _{3} x=\frac{2}{5}\)
- \(\log x=-3\)
- \(\ln x=\frac{1}{2}\)
- Answer
-
1. \(125\)
3. \(\frac{8}{27}\)
5. \(0.001\)
Exercise \(\PageIndex{11}\)
Sketch the graph of the logarithmic function. Draw the vertical asymptote with a dashed line.
- \(f(x)=\log _{2}(x-5)\)
- \(f(x)=\log _{2} x-5\)
- \(g(x)=\log _{3}(x+5)+15\)
- \(g(x)=\log _{3}(x-5)-5\)
- \(h(x)=\log _{4}(-x)+1\)
- \(h(x)=3-\log _{4} x\)
- \(g(x)=\ln (x-2)+3\)
- \(g(x)=\ln (x+3)-1\)
- The population of a certain small town is growing according to the function \(P (t) = 89,000(1.035)^{t}\), where \(t\) represents time in years since the last census. Use the function to estimate the population \(8 \frac{1}{2}\) years after the census was taken.
- The volume of sound \(L\) in decibels (dB) is given by the formula \(L=10 \log \left(I / 10^{-12}\right)\), where \(I\) represents the intensity of the sound in watts per square meter. Determine the volume of a sound with an intensity of \(0.5\) watts per square meter.
- Answer
-
1.
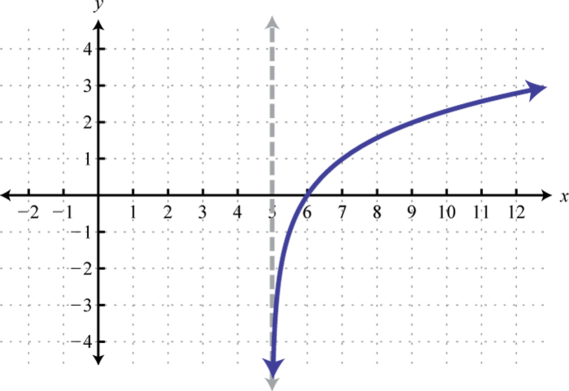
Figure 7.E.11
3.
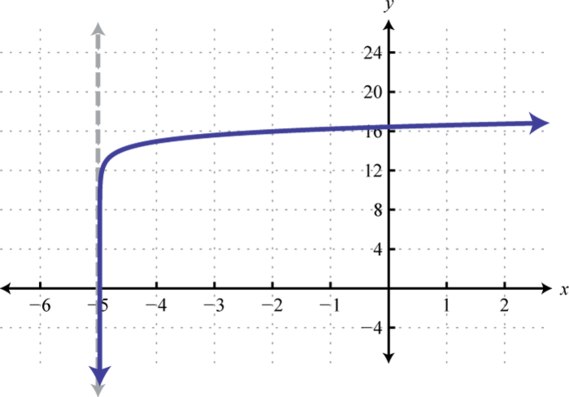
Figure 7.E.12
5.
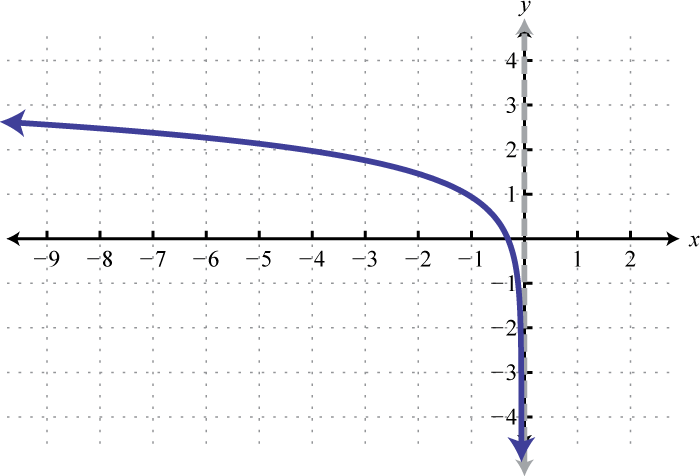
Figure 7.E.13
7.
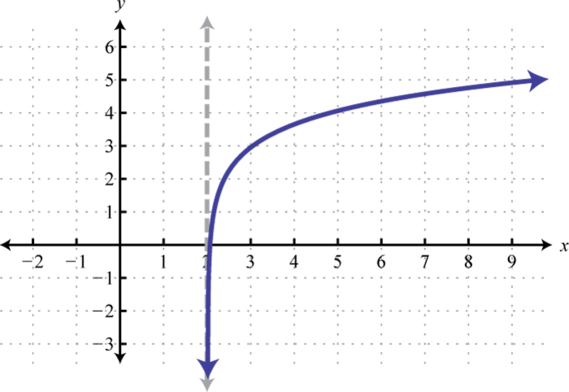
Figure 7.E.14
9. \(119,229\) people
Exercise \(\PageIndex{12}\)
Evaluate without using a calculator.
- \(\log _{9} 9\)
- \(\log _{8} 1\)
- \(\log _{1 / 3} 3\)
- \(\log \left(\frac{1}{10}\right)\)
- \(e^{\ln 17}\)
- \(10^{\log 27}\)
- \(\ln e^{63}\)
- \(\log 10^{33}\)
- Answer
-
1. \(1\)
3. \(−1\)
5. \(17\)
7. \(63\)
Exercise \(\PageIndex{13}\)
Expand completely.
- \(\log \left(100 x^{2}\right)\)
- \(\log _{5}\left(5 x^{3}\right)\)
- \(\log _{3}\left(\frac{3 x^{5}}{5}\right)\)
- \(\ln \left(\frac{10}{3 x^{2}}\right)\)
- \(\log _{2}\left(\frac{8 x^{2}}{y^{2} z}\right)\)
- \(\log \left(\frac{x^{10}}{10 y^{3} z^{4}}\right)\)
- \(\ln \left(\frac{3 b \sqrt{a}}{c^{4}}\right)\)
- \(\log \left(\frac{20 y^{3}}{\sqrt[3]{x^{2}}}\right)\)
- Answer
-
1. \(2+2 \log x\)
3. \(1+5 \log _{3} x-\log _{3} 5\)
5. \(3+2 \log _{2} x-2 \log _{2} y-\log _{2} z\)
7. \(\ln 3+\ln b+\frac{1}{2} \ln a-4 \ln c\)
Exercise \(\PageIndex{14}\)
Write as a single logarithm with coefficient \(1\).
- \(\log x+2 \log y-3 \log z\)
- \(\log _{2} 5-3 \log _{2} x+4 \log _{2} y\)
- \(-2 \log _{5} x+\log _{5} y-5 \log _{5}(x-1)\)
- \(\ln x-\ln (x-1)-\ln (x+1)\)
- \(3 \log _{2} x+\frac{1}{2} \log _{2} y-\frac{2}{3} \log _{2} z\)
- \(\frac{1}{3} \log x-3 \log y-\frac{3}{5} \log z\)
- \(\log _{5} 4+5 \log _{5} x-\frac{1}{3}\left(\log _{5} y+2 \log _{5} z\right)\)
- \(\ln x-\frac{1}{2}(\ln y-4 \ln z)\)
- Answer
-
1. \(\log \left(\frac{x y^{2}}{z^{3}}\right)\)
3. \(\log _{5}\left(\frac{y}{x^{2}(x-1)^{5}}\right)\)
5. \(\log _{2}\left(\frac{x^{3} \sqrt{y}}{\sqrt[3]{z^{2}}}\right)\)
7. \(\log _{5}\left(\frac{4 x^{5}}{\sqrt[3]{y z^{2}}}\right)\)
Exercise \(\PageIndex{15}\)
Solve. Give the exact answer and the approximate answer rounded to the nearest hundredth where appropriate.
- \(5^{2 x+1}=125\)
- \(10^{3 x-2}=100\)
- \(9^{x-3}=81\)
- \(16^{2 x+3}=8\)
- \(5^{x}=7\)
- \(3^{2 x}=5\)
- \(10^{x+2}-3=7\)
- \(e^{2 x-1}+2=3\)
- \(7^{4 x-1}-2=9\)
- \(3^{5 x-2}+5=7\)
- \(3-e^{4 x}=2\)
- \(5+e^{3 x}=4\)
- \(\frac{4}{1+e^{5 x}}=2\)
- \(\frac{100}{1+e^{3 x}}=\frac{1}{2}\)
- Answer
-
1. \(1\)
3. \(5\)
5. \(\frac{\log (7)}{\log (5)} \approx 1.21\)
7. \(-1\)
9. \(\frac{\log 7+\log 11}{4 \log 7} \approx 0.56\)
11. \(0\)
13. \(0\)
Exercise \(\PageIndex{16}\)
Use the change of base formula to approximate the following to the nearest tenth.
- \(\log _{5} 13\)
- \(\log _{2} 27\)
- \(\log _{4} 5\)
- \(\log _{9} 0.81\)
- \(\log _{1 / 4} 21\)
- \(\log _{2} \sqrt[3]{5}\)
- Answer
-
1. \(1.6\)
3. \(1.2\)
5. \(-2.2\)
Exercise \(\PageIndex{17}\)
Solve.
- \(\log _{2}(3 x-5)=\log _{2}(2 x+7)\)
- \(\ln (7 x)=\ln (x+8)\)
- \(\log _{5} 8-2 \log _{5} x=\log _{5} 2\)
- \(\log _{3}(x+2)+\log _{3}(x)=\log _{3} 8\)
- \(\log _{5}(2 x-1)=2\)
- \(2 \log _{4}(3 x-2)=4\)
- \(2=\log _{2}\left(x^{2}-4\right)-\log _{2} 3\)
- \(\log _{2}(x-1)+\log _{2}(x+1)=3\)
- \(\log _{2} x+\log _{2}(x-1)=1\)
- \(\log _{4}(x+5)+\log _{4}(x+11)=2\)
- \(\log (2 x+5)-\log (x-1)=1\)
- \(\ln x-\ln (2 x-1)=1\)
- \(2 \log _{2}(x+4)=\log _{2}(x+2)+3\)
- \(2 \log _{3} x=1+\log _{3}(x+6)\)
- \(\log _{3}(x+1)-2 \log _{3} x=1\)
- \(\log _{5}(2 x)+\log _{5}(x-1)=1\)
- Answer
-
1. \(12\)
3. \(2\)
5. \(13\)
7. \(±4\)
9. \(2\)
11. \(\frac{15}{8}\)
13. \(0\)
15. \(\frac{1+\sqrt{13}}{6}\)
Exercise \(\PageIndex{18}\)
Solve.
- An amount of $\(3,250\) is invested in an account that earns \(4.6\)% annual interest that is compounded monthly. Estimate the number of years for the amount in the account to reach $\(4,000\).
- An amount of $\(2,500\) is invested in an account that earns \(5.5\)% annual interest that is compounded continuously. Estimate the number of years for the amount in the account to reach $\(3,000\).
- How long does it take to double an investment made in an account that earns \(6 \frac{3}{4}\)% annual interest that is compounded continuously?
- How long does it take to double an investment made in an account that earns \(6 \frac{3}{4}\)% annual interest that is compounded semi-annually?
- In the year 2000 a certain small town had a population of \(46,000\) people. In the year 2010 the population was estimated to have grown to \(92,000\) people. If the population continues to grow exponentially at this rate, estimate the population in the year 2016.
- A fleet van was purchased new for $\(28,000\) and \(2\) years later it was valued at $\(20,000\). If the value of the van continues to decrease exponentially at this rate, determine its value \(7\) years after it is purchased new.
- A website that has been in decline registered \(4,200\) unique visitors last month and \(3,600\) unique visitors this month. If the number of unique visitors continues to decline exponentially, how many unique visitors would you expect next month?
- An initial population of \(18\) rabbits was introduced into a wildlife preserve. The number of rabbits doubled in the first year. If the rabbit population continues to grow exponentially at this rate, how many rabbits will be present \(5\) years after they were introduced?
- The half-life of sodium-24 is about \(15\) hours. How long will it take a \(50\)-milligram sample to decay to \(10\) milligrams?
- The half-life of radium-226 is about \(1,600\) years. How long will it take an initial sample to decay to \(30\)% of the original amount?
- An archeologist discovered a bone tool artifact. After analysis, the artifact was found to contain \(62\)% of the carbon-14 normally found in bone from the same animal. Given that carbon-14 has a half-life of \(5,730 years\), estimate the age of the artifact.
- The half-life of radioactive iodine-131 is about \(8\) days. What percentage of an initial sample accidentally released into the atmosphere do we expect to remain after \(53\) days?
- Answer
-
1. \(4.5\) years
3. \(10.27\) years
5. About \(139,446\) people
7. \(3,086\) unique visitors
9. \(35\) hours
11. About \(3,952\) years old
Sample Exam
Exercise \(\PageIndex{19}\)
- Given \(f(x)=x^{2}-x+3\) and \(g(x)=3 x-1\) find \((f \circ g)(x)\).
- Show that \(f(x)=\sqrt[3]{7 x-2} \) and \(g(x)=\frac{x^{3}+2}{7}\) are inverses.
- Answer
-
1. \((f \circ g)(x)=9 x^{2}-9 x+5\)
Exercise \(\PageIndex{20}\)
Find the inverse of the following functions:
- \(f(x)=\frac{1}{2} x-3\)
- \(h(x)=x^{2}+3\) where \(x \geq 0\)
- Answer
-
1. \(f^{-1}(x)=2 x+6\)
Exercise \(\PageIndex{21}\)
Sketch the graph.
- \(f(x)=e^{x}-5\)
- \(g(x)=10^{-x}\)
- Joe invested $\(5,200\) in an account earning \(3.8\)% annual interest that is compounded monthly. How much will be in the account at the end of \(4\) years?
- Mary has $\(3,500\) in a savings account earning \(4 \frac{1}{2}\)% annual interest that is compounded continuously. How much will be in the account at the end of \(3\) years?
- Answer
-
1.
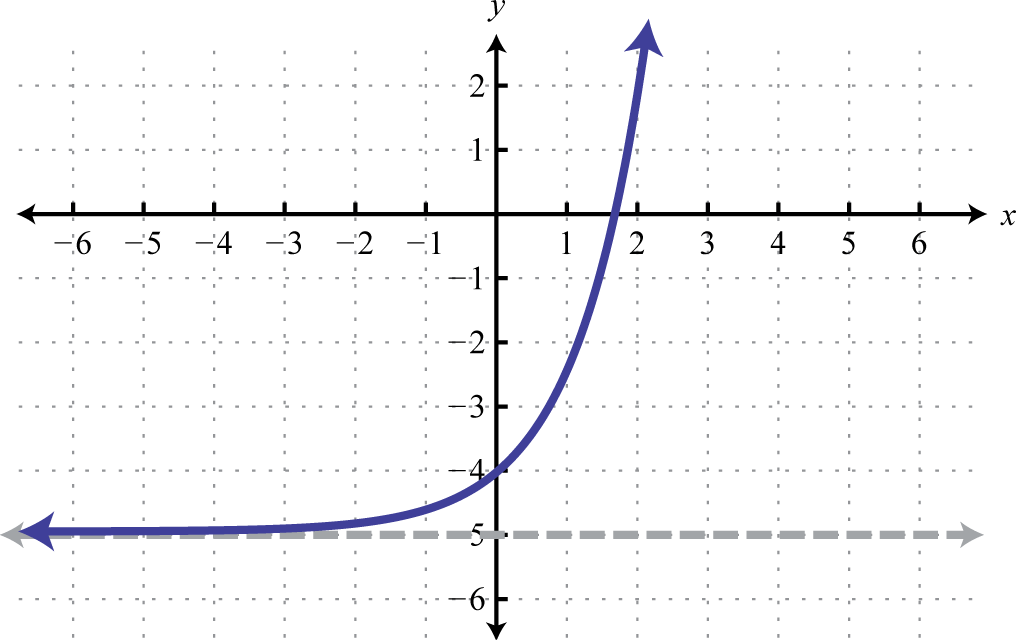
Figure 7.E.15
3. $\(6,052.18\)
Exercise \(\PageIndex{22}\)
Evaluate.
- \(\log _{3} 81\)
- \(\log _{2}\left(\frac{1}{4}\right)\)
- \(\log 1,000\)
- \(\ln e\)
- \(\log _{4} 2\)
- \(\log _{9}\left(\frac{1}{3}\right)\)
- \(\ln e^{3}\)
- \(\log _{1 / 5} 25\)
- Answer
-
1. \(4\)
2. \(-2\)
3. \(3\)
4. \(1\)
Exercise \(\PageIndex{23}\)
Sketch the graph.
- \(f(x)=\log _{4}(x+5)+2\)
- \(f(x)=-\ln (x-2)\)
- Answer
-
1.
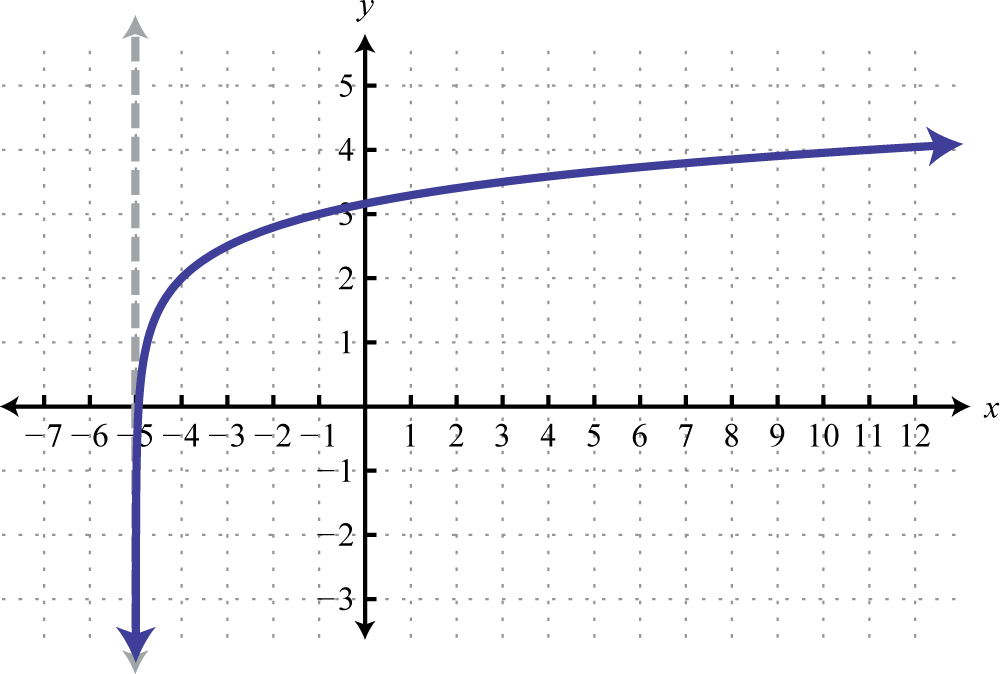
Figure 7.E.16
Exercise \(\PageIndex{24}\)
- Expand: \(\log \left(\frac{100 x^{2} y}{\sqrt{z}}\right)\).
- Write as a single logarithm with coefficient \(1\): \(2 \log _{2} x+\frac{1}{3} \log _{2} y-3 \log _{2} z\).
- Answer
-
1. \(2+2 \log x+\log y-\frac{1}{2} \log z\)
Exercise \(\PageIndex{25}\)
Evaluate. Round off to the nearest tenth.
- \(\log _{2} 10\)
- \(\ln 1\)
- \(\log _{3}\left(\frac{1}{5}\right)\)
- Answer
-
1. \(3.3\)
2. \(0\)
3. \(-1.5\)
Exercise \(\PageIndex{26}\)
Solve:
- \(2^{3 x-1}=16\)
- \(3^{7 x+1}=5\)
- \(\log _{5}(3 x-4)=\log _{5}(2 x+7)\)
- \(\log _{3}\left(x^{2}+26\right)=3\)
- \(\log _{2} x+\log _{2}(2 x+7)=2\)
- \(\log (2 x+3)=1+\log (x+1)\)
- Joe invested $\(5,200\) in an account earning \(3.8\)% annual interest that is compounded monthly. How long will it take to accumulate a total of $\(6,200\) in the account?
- Mary has $\(3,500\) in a savings account earning \(4 \frac{1}{2}\)% annual interest that is compounded continuously. How long will it take to double the amount in the account?
- During the exponential growth phase, certain bacteria can grow at a rate of \(5.3\)% per hour. If \(12,000\) cells are initially present in a sample, construct an exponential growth model and use it to:
- Estimate the population of bacteria in \(3.5\) hours.
- Estimate the time it will take the population to double.
- The half-life of caesium-137 is about \(30\) years. Approximate the time it will take a \(20\)-milligram sample of caesium-137 to decay to \(8\) milligrams.
- Answer
-
2. \(\frac{\log 5-\log 3}{7 \log 3}\)
4. \(\pm 1\)
6. \(-\frac{7}{8}\)
8. \(15.4\) years
10. \(40\) years


