2.3: Models and Applications

Learning Objectives

• Set up a linear equation to solve a real-world application.
• Use a formula to solve a real-world application.

Josh is hoping to get an in his college algebra class. He has scores of , , , , and on his first five tests. Only the final exam remains, and the maximum of points that can be earned is . Is it possible for Josh to end the course with an ? A simple linear equation will give Josh his answer.

Figure 2.4.1 Credit: Kevin Dooley

Many real-world applications can be modeled by linear equations. For example, a cell phone package may include a monthly service fee plus a charge per minute of talk-time; it costs a widget manufacturer a certain amount to produce x widgets per month plus monthly operating charges; a car rental company charges a daily fee plus an amount per mile driven. These are examples of applications we come across every day that are modeled by linear equations. In this section, we will set up and use linear equations to solve such problems.

Setting up a Linear Equation to Solve a Real-World Application

To set up or model a linear equation to fit a real-world application, we must first determine the known quantities and define the unknown quantity as a variable. Then, we begin to interpret the words as mathematical expressions using mathematical symbols. Let us use the car rental example above. In this case, a known cost, such as , is multiplied by an unknown quantity, the number of miles driven. Therefore, we can write . This expression represents a variable cost because it changes according to the number of miles driven.

If a quantity is independent of a variable, we usually just add or subtract it, according to the problem. As these amounts do not change, we call them fixed costs. Consider a car rental agency that charges plus a daily fee of . We can use these quantities to model an equation that can be used to find the daily car rental cost .

When dealing with real-world applications, there are certain expressions that we can translate directly into math. Table lists some common verbal expressions and their equivalent mathematical expressions.

Table : Verbal to math conversion

Verbal	Translation to Math Operations
One number exceeds another by a
Twice a number
One number is more than another number
One number is a less than twice another number
The product of a number and , decreased by
The quotient of a number and the number plus is three times the number
The product of three times a number and the number decreased by is

How to: Given a real-world problem, model a linear equation to fit it

1. Identify known quantities.
2. Assign a variable to represent the unknown quantity.
3. If there is more than one unknown quantity, find a way to write the second unknown in terms of the first.
4. Write an equation interpreting the words as mathematical operations.
5. Solve the equation. Be sure the solution can be explained in words, including the units of measure.

Example

Find a linear equation to solve for the following unknown quantities: One number exceeds another number by and their sum is . Find the two numbers.

Solution

Let equal the first number. Then, as the second number exceeds the first by , we can write the second number as . The sum of the two numbers is . We usually interpret the word is as an equal sign.

The two numbers are and .

Exercise

Find a linear equation to solve for the following unknown quantities: One number is three more than twice another number. If the sum of the two numbers is , find the numbers.

Answer

and

Example : Setting Up a Equation to Solve a Real-World Application

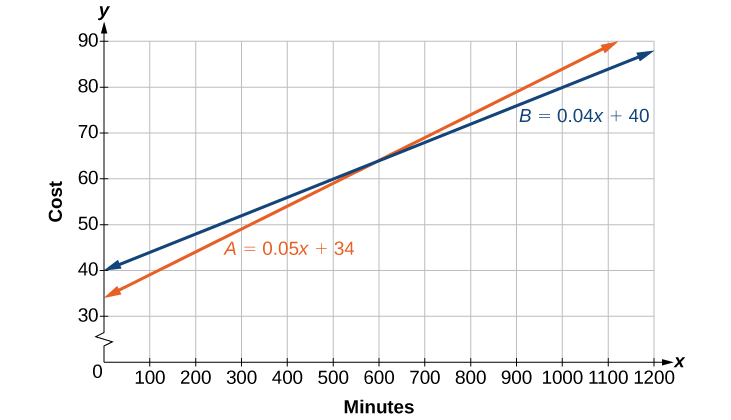
There are two cell phone companies that offer different packages. Company A charges a monthly service fee of plus talk-time. Company B charges a monthly service fee of plus talk-time.

1. Write a linear equation that models the packages offered by both companies.
2. If the average number of minutes used each month is , which company offers the better plan?
3. If the average number of minutes used each month is , which company offers the better plan?
4. How many minutes of talk-time would yield equal monthly statements from both companies?

Solution

a.

The model for Company A can be written as . This includes the variable cost of plus the monthly service charge of . Company B’s package charges a higher monthly fee of , but a lower variable cost of . Company B’s model can be written as .

b.

If the average number of minutes used each month is , we have the following:

So, Company B offers the lower monthly cost of as compared with the monthly cost offered by Company A when the average number of minutes used each month is .

c.

If the average number of minutes used each month is , we have the following:

If the average number of minutes used each month is , then Company A offers a lower monthly cost of compared to Company B’s monthly cost of .

d.

To answer the question of how many talk-time minutes would yield the same bill from both companies, we should think about the problem in terms of coordinates: At what point are both the -value and the -value equal? We can find this point by setting the equations equal to each other and solving for .

Check the -value in each equation.

Therefore, a monthly average of talk-time minutes renders the plans equal. See Figure .

Figure

Exercise

Find a linear equation to model this real-world application: It costs ABC electronics company per unit to produce a part used in a popular brand of desktop computers. The company has monthly operating expenses of for utilities and for salaries. What are the company’s monthly expenses?

Answer

Using a Formula to Solve a Real-World Application

Many applications are solved using known formulas. The problem is stated, a formula is identified, the known quantities are substituted into the formula, the equation is solved for the unknown, and the problem’s question is answered. Typically, these problems involve two equations representing two trips, two investments, two areas, and so on. Examples of formulas include the area of a rectangular region,

the perimeter of a rectangle,

and the volume of a rectangular solid,

When there are two unknowns, we find a way to write one in terms of the other because we can solve for only one variable at a time.

Example : Solving an Application Using a Formula

It takes Andrew to drive to work in the morning. He drives home using the same route, but it takes \(10\; min\) longer, and he averages less than in the morning. How far does Andrew drive to work?

Solution

This is a distance problem, so we can use the formula , where distance equals rate multiplied by time. Note that when rate is given in , time must be expressed in hours. Consistent units of measurement are key to obtaining a correct solution.

First, we identify the known and unknown quantities. Andrew’s morning drive to work takes , or at rate . His drive home takes , or , and his speed averages less than the morning drive. Both trips cover distance . A table, such as Table , is often helpful for keeping track of information in these types of problems.

Table

To Work
To Home

Write two equations, one for each trip.

As both equations equal the same distance, we set them equal to each other and solve for .

We have solved for the rate of speed to work, . Substituting into the rate on the return trip yields . Now we can answer the question. Substitute the rate back into either equation and solve for .

The distance between home and work is .

Analysis

Note that we could have cleared the fractions in the equation by multiplying both sides of the equation by the LCD to solve for .

Exercise

On Saturday morning, it took Jennifer to drive to her mother’s house for the weekend. On Sunday evening, due to heavy traffic, it took Jennifer to return home. Her speed was slower on Sunday than on Saturday. What was her speed on Sunday?

Answer

Example : Solving a Perimeter Problem

The perimeter of a rectangular outdoor patio is . The length is greater than the width. What are the dimensions of the patio?

Solution

The perimeter formula is standard: . We have two unknown quantities, length and width. However, we can write the length in terms of the width as . Substitute the perimeter value and the expression for length into the formula. It is often helpful to make a sketch and label the sides as in Figure .

Figure

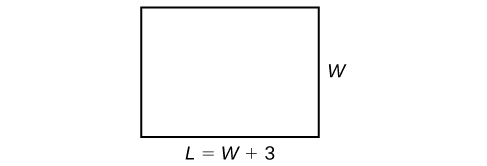
Now we can solve for the width and then calculate the length.

The dimensions are and .

Exercise

Find the dimensions of a rectangle given that the perimeter is and the length is more than twice the width.

Answer

,

Example : Solving an Area Problem

The perimeter of a tablet of graph paper is . The length is . more than the width. Find the area of the graph paper.

Solution

The standard formula for area is ; however, we will solve the problem using the perimeter formula. The reason we use the perimeter formula is because we know enough information about the perimeter that the formula will allow us to solve for one of the unknowns. As both perimeter and area use length and width as dimensions, they are often used together to solve a problem such as this one.

We know that the length is . more than the width, so we can write length as . Substitute the value of the perimeter and the expression for length into the perimeter formula and find the length.

Now, we find the area given the dimensions of . and .

The area is .

Exercise

A game room has a perimeter of . The length is five more than twice the width. How many of new carpeting should be ordered?

Answer

Example : Solving a Volume Problem

Find the dimensions of a shipping box given that the length is twice the width, the height is in, and the volume is .

Solution

The formula for the volume of a box is given as , the product of length, width, and height. We are given that , and . The volume is .

The dimensions are , , and .

Analysis

Note that the square root of would result in a positive and a negative value. However, because we are describing width, we can use only the positive result.

Media

Access these online resources for additional instruction and practice with models and applications of linear equations.

1. Problem solving using linear equations
2. Problem solving using equations
3. Finding the dimensions of area given the perimeter
4. Find the distance between the cities using the distance = rate * time formula
5. Linear equation application (Write a cost equation)

Key Concepts

• A linear equation can be used to solve for an unknown in a number problem. See Example.
• Applications can be written as mathematical problems by identifying known quantities and assigning a variable to unknown quantities. See Example.
• There are many known formulas that can be used to solve applications. Distance problems, for example, are solved using the formula. See Example.
• Many geometry problems are solved using the perimeter formula , the area formula , or the volume formula . See Example, Example, and Example.