9.2: Sum and Difference Identities

Learning Objectives

• Use sum and difference formulas for cosine.
• Use sum and difference formulas for sine.
• Use sum and difference formulas for tangent.
• Use sum and difference formulas for cofunctions.
• Use sum and difference formulas to verify identities.

How can the height of a mountain be measured? What about the distance from Earth to the sun? Like many seemingly impossible problems, we rely on mathematical formulas to find the answers. The trigonometric identities, commonly used in mathematical proofs, have had real-world applications for centuries, including their use in calculating long distances.

The trigonometric identities we will examine in this section can be traced to a Persian astronomer who lived around 950 AD, but the ancient Greeks discovered these same formulas much earlier and stated them in terms of chords. These are special equations or postulates, true for all values input to the equations, and with innumerable applications.

Figure $\PageIndex{1}$: Mount McKinley, in Denali National Park, Alaska, rises 20,237 feet (6,168 m) above sea level. It is the highest peak in North America. (credit: Daniel A. Leifheit, Flickr)

In this section, we will learn techniques that will enable us to solve problems such as the ones presented above. The formulas that follow will simplify many trigonometric expressions and equations. Keep in mind that, throughout this section, the term formula is used synonymously with the word identity.

Using the Sum and Difference Formulas for Cosine

Finding the exact value of the sine, cosine, or tangent of an angle is often easier if we can rewrite the given angle in terms of two angles that have known trigonometric values. We can use the special angles, which we can review in the unit circle shown in Figure $\PageIndex{2}$.

Figure $\PageIndex{2}$: The Unit Circle

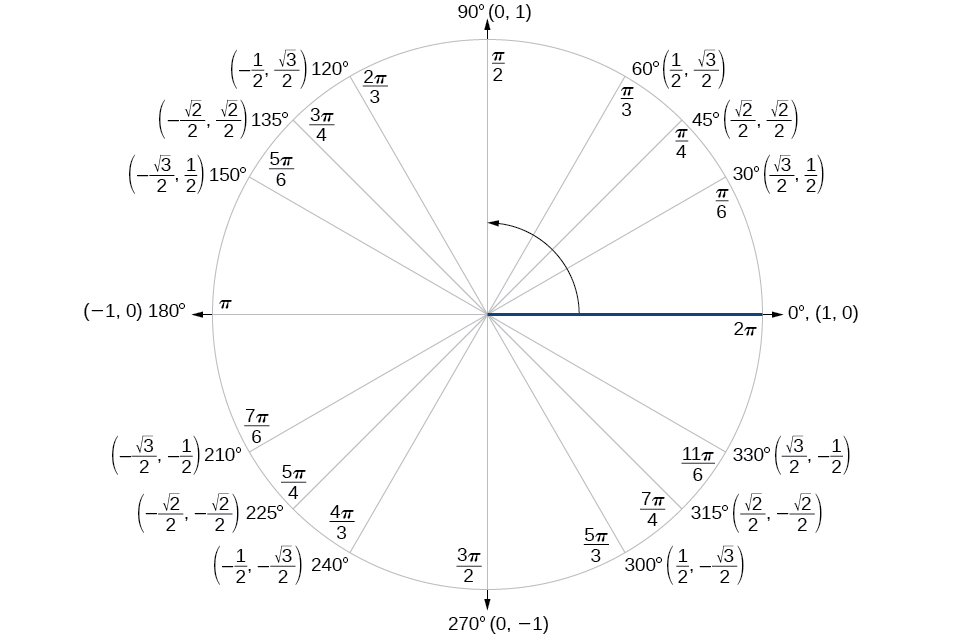
We will begin with the sum and difference formulas for cosine, so that we can find the cosine of a given angle if we can break it up into the sum or difference of two of the special angles (Table $\PageIndex{1}$).

Table $\PageIndex{1}$

Sum formula for cosine	$\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta$
Difference formula for cosine	$\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta$

First, we will prove the difference formula for cosines. Let’s consider two points on the unit circle (Figure $\PageIndex{3}$). Point $P$ is at an angle $\alpha$ from the positive $x$-axis with coordinates $(\cos \alpha,\sin \alpha)$ and point $Q$ is at an angle of $\beta$ from the positive $x$-axis with coordinates $(\cos \beta,\sin \beta)$. Note the measure of angle $POQ$ is $\alpha−\beta$.

Label two more points: $A$ at an angle of $(\alpha−\beta)$ from the positive $x$-axis with coordinates $(\cos(\alpha−\beta),\sin(\alpha−\beta))$; and point $B$ with coordinates $(1,0)$. Triangle $POQ$ is a rotation of triangle $AOB$ and thus the distance from $P$ to $Q$ is the same as the distance from $A$ to $B$.

Figure $\PageIndex{3}$

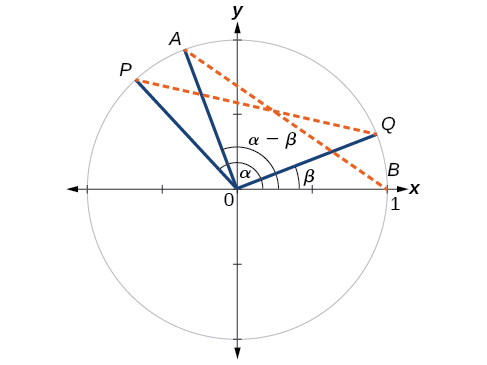
We can find the distance from $P$ to $Q$ using the distance formula.

$$\begin{align*} d_{PQ}&= \sqrt{{(\cos \alpha - \cos \beta )}^2+{(sin \alpha - sin \beta )}^2}\\[4pt] &= \sqrt{{\cos}^2 \alpha-2\cos \alpha \cos \beta+{\cos}^2 \beta+{\sin}^2 \alpha-2\sin \alpha \sin \beta+{\sin}^2 \beta} & & \text {Apply Pythagorean identity and simplify.}\\[4pt] &= \sqrt{({\cos}^2 \alpha+{\sin}^2 \alpha)+({\cos}^2 \beta+{\sin}^2 \beta)-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}\\[4pt] &= \sqrt{1+1-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}\\[4pt] &= \sqrt{2-2\cos \alpha \cos \beta-2\sin \alpha \sin \beta}\end{align*}$$

Similarly, using the distance formula we can find the distance from $A$ to $B$.

$$\begin{align*} d_{AB}&= \sqrt{{(\cos(\alpha-\beta)-1)}^2+{(\sin(\alpha-\beta)-0)}^2}\\[4pt] &= \sqrt{{\cos}^2(\alpha-\beta)-2\cos(\alpha-\beta)+1+{\sin}^2(\alpha-\beta)} & & \text {Apply Pythagorean identity and simplify}\\[4pt] &= \sqrt{({\cos}^2(\alpha-\beta)+{\sin}^2(\alpha-\beta))-2\cos(\alpha-\beta)+1}\\[4pt] &= \sqrt{1-2\cos(\alpha-\beta)+1}\\[4pt] &= \sqrt{2-2\cos(\alpha-\beta)} & & \text {Subtract 2 from both sides and divide both sides by −2.}\\[4pt] \cos \alpha \cos \beta+\sin \alpha \sin \beta&= \cos(\alpha-\beta) \end{align*}$$

Thus, we have the difference formula for cosine. We can use similar methods to derive the cosine of the sum of two angles.

SUM AND DIFFERENCE FORMULAS FOR COSINE

These formulas can be used to calculate the cosine of sums and differences of angles.

$$\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta$$

$$\cos(\alpha−\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta$$

How to: Given two angles, find the cosine of the difference between the angles

1. Write the difference formula for cosine.
2. Substitute the values of the given angles into the formula.
3. Simplify.

Example $\PageIndex{1}$: Finding the Exact Value Using the Formula for the Cosine of the Difference of Two Angles

Using the formula for the cosine of the difference of two angles, find the exact value of $\cos\left(\dfrac{5\pi}{4}−\dfrac{\pi}{6}\right)$.

Solution

Begin by writing the formula for the cosine of the difference of two angles. Then substitute the given values.

$$\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos\left(\dfrac{5\pi}{4}-\dfrac{\pi}{6}\right)&= \cos\left(\dfrac{5\pi}{4}\right)\cos\left(\dfrac{\pi}{6}\right)+\sin\left(\dfrac{5\pi}{4}\right)\sin\left(\dfrac{\pi}{6}\right)\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{\sqrt{3}}{2}\right)-\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{1}{2}\right)\\[4pt] &= -\dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{-\sqrt{6}-\sqrt{2}}{4} \end{align*}$$

Keep in mind that we can always check the answer using a graphing calculator in radian mode.

Exercise $\PageIndex{1}$:

Find the exact value of $\cos\left(\dfrac{\pi}{3}−\dfrac{\pi}{4}\right)$.

Answer

$\dfrac{\sqrt{2}+\sqrt{6}}{4}$

Example $\PageIndex{2}$: Finding the Exact Value Using the Formula for the Sum of Two Angles for Cosine

Find the exact value of $\cos(75°)$.

Solution

As $75°=45°+30°$,we can evaluate $\cos(75°)$ as $\cos(45°+30°)$.

$$\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta -\sin \alpha \sin \beta\\[4pt] \cos(45^{\circ}+30^{\circ})&= \cos(45^{\circ})\cos(30^{\circ})-\sin(45^{\circ})\sin(30^{\circ})\\[4pt] &= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}}{4}-\dfrac{\sqrt{2}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}$$

Keep in mind that we can always check the answer using a graphing calculator in degree mode.

Analysis

Note that we could have also solved this problem using the fact that $75°=135°−60°$.

$$\begin{align*} \cos(\alpha-\beta)&= \cos \alpha \cos \beta+\sin \alpha \sin \beta\\[4pt] \cos(135^{\circ}-60^{\circ})&= \cos(135^{\circ})\cos(60^{\circ})+\sin(135^{\circ})\sin(60^{\circ})\\[4pt] &= \left(-\dfrac{\sqrt{2}}{2}\right)\left(\dfrac{1}{2}\right)+\left(\dfrac{\sqrt{2}}{2}\right )\left(\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= -\dfrac{\sqrt{2}}{4}+\dfrac{\sqrt{6}}{4}\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}$$

Exercise $\PageIndex{2}$

Find the exact value of $\cos(105°)$.

Answer

$\dfrac{\sqrt{2}-\sqrt{6}}{4}$

Using the Sum and Difference Formulas for Sine

The sum and difference formulas for sine can be derived in the same manner as those for cosine, and they resemble the cosine formulas.

SUM AND DIFFERENCE FORMULAS FOR SINE

These formulas can be used to calculate the sines of sums and differences of angles.

$$\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta$$

$$\sin(\alpha−\beta)=\sin \alpha \cos \beta−\cos \alpha \sin \beta$$

How to: Given two angles, find the sine of the difference between the angles

1. Write the difference formula for sine.
2. Substitute the given angles into the formula.
3. Simplify.

Example $\PageIndex{3}$: Using Sum and Difference Identities to Evaluate the Difference of Angles

Use the sum and difference identities to evaluate the difference of the angles and show that part a equals part b.

1. $\sin(45°−30°)$
2. $\sin(135°−120°)$

Solution

1. Let’s begin by writing the formula and substitute the given angles.

$$\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(45^{\circ}-30^{\circ})&= \sin(45^{\circ})\cos(30^{\circ})-\cos(45^{\circ})\sin(30^{\circ}) \end{align*}$$

Next, we need to find the values of the trigonometric expressions.

$\sin(45°)=\frac{\sqrt{2}}{2}, \qquad \cos(30°)=\frac{\sqrt{3}}{2}, \qquad \cos(45°)=\frac{\sqrt{2}}{2}, \qquad \sin(30°)=\frac{1}{2}$

Now we can substitute these values into the equation and simplify.

$$\begin{align*} \sin(45°-30°)&= \dfrac{\sqrt{2}}{2}\left(\dfrac{\sqrt{3}}{2}\right)-\dfrac{\sqrt{2}}{2}\left(\dfrac{1}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}$$

2. Again, we write the formula and substitute the given angles.

$$\begin{align*} \sin(\alpha-\beta)&= \sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] \sin(135^{\circ}-120^{\circ})&= \sin(135^{\circ})\cos(120^{\circ})-\cos(135^{\circ})\sin(120^{\circ}) \end{align*}$$

Next, we find the values of the trigonometric expressions.

$\sin(135°)=\frac{\sqrt{2}}{2}, \qquad \cos(120°)=-\frac{1}{2}, \qquad \cos(135°)=\frac{\sqrt{2}}{2}, \qquad \sin(120°)=\frac{\sqrt{3}}{2}$

Now we can substitute these values into the equation and simplify.

$$\begin{align*} \sin(135^{\circ}-120^{\circ})&= \dfrac{\sqrt{2}}{2}\left(-\dfrac{1}{2}\right)-\left(-\dfrac{\sqrt{2}}{2}\right)\left (\dfrac{\sqrt{3}}{2}\right)\\[4pt] &= \dfrac{\sqrt{6}-\sqrt{2}}{4} \end{align*}$$

Example $\PageIndex{4}$: Finding the Exact Value of an Expression Involving an Inverse Trigonometric Function

Find the exact value of $\sin\left ({\cos}^{−1}\frac{1}{2}+{\sin}^{−1}\frac{3}{5}\right)$. Then check the answer with a graphing calculator.

Solution

The pattern displayed in this problem is $\sin(\alpha+\beta)$. Let $\alpha={\cos}^{−1}\frac{1}{2}$ and $\beta={\sin}^{−1}\frac{3}{5}$. Then we can write

$$\begin{align*} \cos \alpha&= \dfrac{1}{2}, \quad 0\leq \alpha\leq \pi\\[4pt] \sin \beta&= \dfrac{3}{5}, \quad - \dfrac{\pi}{2}\leq \beta\leq \dfrac{\pi}{2}\\[4pt]\end{align*}$$

We will use the Pythagorean identities to find $\sin \alpha$ and $\cos \beta$

$$\begin{align*} \sin \alpha&= \sqrt{1-{\cos}^2 \alpha}\\[4pt] &= \sqrt{1-\dfrac{1}{4}}\\[4pt] &= \sqrt{\dfrac{3}{4}}\\[4pt] &= \dfrac{\sqrt{3}}{2}\\[4pt] \cos \beta&= \sqrt{1-{\sin}^2 \beta}\\[4pt] &= \sqrt{1-\dfrac{9}{25}}\\[4pt] &= \sqrt{\dfrac{16}{25}}\\[4pt] &= \dfrac{4}{5} \end{align*}$$

Using the sum formula for sine,

$$\begin{align*} \sin \left({\cos}^{-1}\tfrac{1}{2}+{\sin}^{-1}\tfrac{3}{5}\right)&= \sin(\alpha+\beta)\\[4pt] &= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt] &= \dfrac{\sqrt{3}}{2}\cdot \dfrac{4}{5}+\dfrac{1}{2}\cdot \dfrac{3}{5}\\[4pt] &= \dfrac{4\sqrt{3}+3}{10} \end{align*}$$

Using the Sum and Difference Formulas for Tangent

Finding exact values for the tangent of the sum or difference of two angles is a little more complicated, but again, it is a matter of recognizing the pattern.

Finding the sum of two angles formula for tangent involves taking quotient of the sum formulas for sine and cosine and simplifying. Recall, $\tan x=\dfrac{\sin x}{\cos x}$, when $\cos x≠0$.

Let’s derive the sum formula for tangent.

$$\begin{align*} \tan\left (\alpha+\beta\right)&= \dfrac{\sin\left (\alpha+\beta\right )}{\cos(\alpha+\beta)}\\[6pt] &= \dfrac{\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta-\sin \alpha \sin \beta}\\[6pt] &= \dfrac{\dfrac{\sin \alpha \cos \beta+\cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{\dfrac{\cos \alpha \cos \beta-\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}\\[6pt] &= \dfrac{\dfrac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}+\dfrac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta}}{\dfrac{\cos \alpha \cos \beta}{\cos \alpha \cos \beta}-\dfrac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}\\[6pt] &= \dfrac{\dfrac{\sin \alpha}{\cos \alpha}+\dfrac{\sin \beta}{\cos \beta}}{1-\dfrac{\sin \alpha \sin \beta}{\cos \alpha \cos \beta}}\\[6pt] &= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta} \end{align*}$$

We can derive the difference formula for tangent in a similar way.

SUM AND DIFFERENCE FORMULAS FOR TANGENT

The sum and difference formulas for tangent are:

$$\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1−\tan \alpha \tan \beta}$$

$$\tan(\alpha-\beta)=\dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}$$

How to: Given two angles, find the tangent of the sum of the angles

1. Write the sum formula for tangent.
2. Substitute the given angles into the formula.
3. Simplify.

Example $\PageIndex{5}$: Finding the Exact Value of an Expression Involving Tangent

Find the exact value of $\tan\left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)$.

Solution

Let’s first write the sum formula for tangent and then substitute the given angles into the formula.

$$\begin{align*} \tan(\alpha+\beta)&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta} \\[4pt] \tan\left(\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)&= \dfrac{\tan\left (\dfrac{\pi}{6}\right)+\tan\left (\dfrac{\pi}{4}\right )}{1-\left (\tan\left (\dfrac{\pi}{6}\right ) \right )\left (\tan\left (\dfrac{\pi}{4}\right )\right )}\end{align*}$$

Next, we determine the individual function values within the formula:

$$\tan\left (\dfrac{\pi}{6}\right )= \dfrac{1}{\sqrt{3}}, \quad \text{and} \quad \tan\left (\dfrac{\pi}{4}\right) = 1$$
So we have,
$$\begin{align*}\tan\left (\dfrac{\pi}{6}+\dfrac{\pi}{4}\right)&= \dfrac{\dfrac{1}{\sqrt{3}}+1}{1-\left(\dfrac{1}{\sqrt{3}}\right )(1)}\\[6pt] &= \dfrac{\dfrac{1+\sqrt{3}}{\sqrt{3}}}{\dfrac{\sqrt{3}-1}{\sqrt{3}}}\\[6pt] &= \dfrac{1+\sqrt{3}}{\sqrt{3}}\cdot\dfrac{\sqrt{3}}{\sqrt{3}-1}\\[6pt] &= \dfrac{\sqrt{3}+1}{\sqrt{3}-1} \end{align*}$$

Exercise $\PageIndex{5}$:

Find the exact value of $\tan\left (\dfrac{2\pi}{3}+\dfrac{\pi}{4}\right )$.

Answer

$\dfrac{1-\sqrt{3}}{1+\sqrt{3}}$

Example $\PageIndex{6}$: Finding Multiple Sums and Differences of Angles

Given $\sin \alpha=\frac{3}{5}, \quad 0<\alpha<\frac{\pi}{2},$ and $\cos \beta=−\frac{5}{13}, \quad \pi<\beta<\frac{3\pi}{2}$,

find

1. $\sin(\alpha+\beta)$
2. $\cos(\alpha+\beta)$
3. $\tan(\alpha+\beta)$
4. $\tan(\alpha−\beta)$

Solution

We can use the sum and difference formulas to identify the sum or difference of angles when the ratio of sine, cosine, or tangent is provided for each of the individual angles. To do so, we construct what is called a reference triangle to help find each component of the sum and difference formulas.

1. To find $\sin(\alpha+\beta)$, we begin with $\sin \alpha=\dfrac{3}{5}$ and $0<\alpha<\dfrac{\pi}{2}$. The side opposite $\alpha$ has length 3, the hypotenuse has length 5, and $\alpha$ is in the first quadrant. See Figure $\PageIndex{4}$. Using the Pythagorean Theorem, we can find the length of side $a$:

$$\begin{align*} a^2+3^2&= 5^2\\[4pt] a^2&= 16\\[4pt] a&= 4 \end{align*}$$

Figure $\PageIndex{4}$

Since $\cos \beta=−\dfrac{5}{13}$ and $\pi<\beta<\dfrac{3\pi}{2}$,the side adjacent to $\beta$ is $−5$,the hypotenuse is $13$, and $\beta$ is in the third quadrant. See Figure $\PageIndex{5}$. Again, using the Pythagorean Theorem, we have

$$\begin{align*} {(-5)}^2+a^2&= {13}^2\\[4pt] 25+a^2&= 169\\[4pt] a^2&= 144\\[4pt] a&= \pm 12 \end{align*}$$

Since $\beta$ is in the third quadrant, $a=–12$.

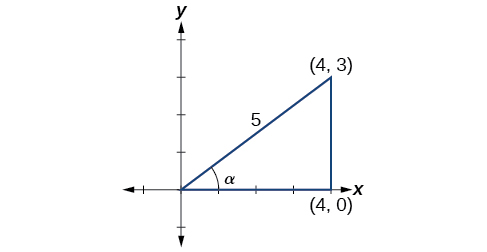
Figure $\PageIndex{5}$

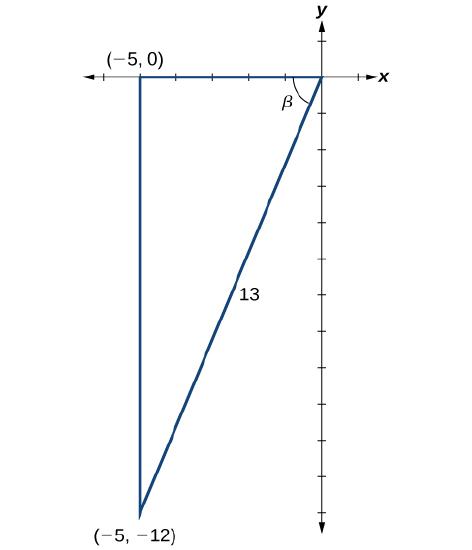
The next step is finding the cosine of $\alpha$ and the sine of $\beta$. The cosine ofα α is the adjacent side over the hypotenuse. We can find it from the triangle in Figure $\PageIndex{5}$: $\cos \alpha=\dfrac{4}{5}$. We can also find the sine of $\beta$ from the triangle in Figure $\PageIndex{5}$, as opposite side over the hypotenuse: $\sin \beta=−\dfrac{12}{13}$. Now we are ready to evaluate $\sin(\alpha+\beta)$.

$$\begin{align*} \sin(\alpha+\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta\\[4pt] &= \left(\dfrac{3}{5}\right)\left(-\dfrac{5}{13}\right )+\left (\dfrac{4}{5}\right )\left(-\dfrac{12}{13}\right )\\[4pt] &= -\dfrac{15}{65}-\dfrac{48}{65}\\[4pt] &= -\dfrac{63}{65} \end{align*}$$

2. We can find $\cos(\alpha+\beta)$ in a similar manner. We substitute the values according to the formula.

$$\begin{align*} \cos(\alpha+\beta)&= \cos \alpha \cos \beta-\sin \alpha \sin \beta\\[4pt] &= \left(\dfrac{4}{5}\right)\left(-\dfrac{5}{13}\right)-\left(\dfrac{3}{5}\right )\left(-\dfrac{12}{13}\right)\\[4pt] &= -\dfrac{20}{65}+\dfrac{36}{65}\\[4pt] &= \dfrac{16}{65} \end{align*}$$

3. For $\tan(\alpha+\beta)$,if $\sin \alpha=\dfrac{3}{5}$ and $\cos \alpha=\dfrac{4}{5}$, then

$\tan \alpha=\dfrac{\dfrac{3}{5}}{\dfrac{4}{5}}=\dfrac{3}{4}$

If $\sin \beta=−\dfrac{12}{13}$ and $\cos \beta=−\dfrac{5}{13}$, then

$\tan \beta=\dfrac{−\dfrac{12}{13}}{−\dfrac{5}{13}}=\dfrac{12}{5}$

Then,

$$\begin{align*} \tan(\alpha+\beta)&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\\[6pt] &= \dfrac{\dfrac{3}{4}+\dfrac{12}{5}}{1-\dfrac{3}{4}\left(\dfrac{12}{5}\right)}\\[6pt] &= \dfrac{\dfrac{63}{20}}{-\dfrac{16}{20}}\\[6pt] &= -\dfrac{63}{16} \end{align*}$$

4. To find $\tan(\alpha−\beta)$, we have the values we need. We can substitute them in and evaluate.

$$\begin{align*} \tan(\alpha-\beta)&= \dfrac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta}\\[6pt] &= \dfrac{\dfrac{3}{4}-\dfrac{12}{5}}{1+\dfrac{3}{4}\left(\dfrac{12}{5}\right)}\\[6pt] &= \dfrac{-\dfrac{33}{20}}{\dfrac{56}{20}}\\[6pt] &= -\dfrac{33}{56} \end{align*}$$

Analysis

A common mistake when addressing problems such as this one is that we may be tempted to think that $\alpha$ and $\beta$ are angles in the same triangle, which of course, they are not. Also note that

$\tan(\alpha+\beta)=\sin(\alpha+\beta)\cos(\alpha+\beta)$

Using Sum and Difference Formulas for Cofunctions

Now that we can find the sine, cosine, and tangent functions for the sums and differences of angles, we can use them to do the same for their cofunctions. You may recall from Right Triangle Trigonometry that, if the sum of two positive angles is $\frac{\pi}{2}$, those two angles are complements, and the sum of the two acute angles in a right triangle is $\frac{\pi}{2}$, so they are also complements. In Figure $\PageIndex{6}$, notice that if one of the acute angles is labeled as $\theta$, then the other acute angle must be labeled $\frac{\pi}{2}−\theta$.

Notice also that $\sin \theta=\cos\left(\frac{\pi}{2}−\theta\right)$,which is opposite over hypotenuse. Thus, when two angles are complimentary, we can say that the sine of $\theta$ equals the cofunction of the complement of $\theta$. Similarly, tangent and cotangent are cofunctions, and secant and cosecant are cofunctions.

Figure $\PageIndex{6}$

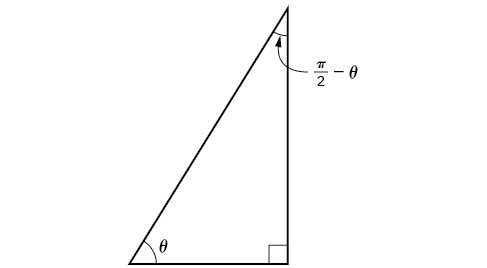
From these relationships, the cofunction identities are formed. Recall that you first encountered these identities in The Unit Circle: Sine and Cosine Functions.

COFUNCTION IDENTITIES

The cofunction identities are summarized in Table $\PageIndex{2}$.

Table $\PageIndex{2}$

$\sin \theta=\cos\left(\dfrac{\pi}{2}−\theta\right)$	$\cos \theta=\sin\left(\dfrac{\pi}{2}−\theta\right)$
$\tan \theta=\cot\left(\dfrac{\pi}{2}−\theta\right)$	$\cot \theta=\tan\left(\dfrac{\pi}{2}−\theta\right )$
$\sec \theta=\csc\left (\dfrac{\pi}{2}−\theta\right )$	$\csc \theta=\sec\left (\dfrac{\pi}{2}−\theta\right )$

Notice that the formulas in the table may also justified algebraically using the sum and difference formulas. For example, using

$\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta$

We can write

$$\begin{align*} \cos\left (\dfrac{\pi}{2}-\theta \right )&= \cos \dfrac{\pi}{2} \cos \theta+\sin \dfrac{\pi}{2} \sin \theta \\[4pt] &=(0)\cos \theta+(1)\sin \theta \\[4pt] &=\sin \theta \end{align*}$$

Example $\PageIndex{7}$: Finding a Cofunction with the Same Value as the Given Expression

Write $\tan \dfrac{\pi}{9}$ in terms of its cofunction.

Solution

The cofunction of $\tan \theta=\cot\left (\dfrac{\pi}{2}−\theta\right )$. Thus,

$$\begin{align*} \tan\left (\dfrac{\pi}{9}\right )&= \cot\left (\dfrac{\pi}{2}-\dfrac{\pi}{9}\right )\\[4pt] &= \cot\left (\dfrac{9\pi}{18}-\dfrac{2\pi}{18}\right )\\[4pt] &= \cot\left (\dfrac{7\pi}{18}\right ) \end{align*}$$

Exercise $\PageIndex{7}$

​​​​​Write $\sin \dfrac{\pi}{7}$ in terms of its cofunction.

Answer

$\cos\left (\dfrac{5\pi}{14}\right )$

Using the Sum and Difference Formulas to Verify Identities

Verifying an identity means demonstrating that the equation holds for all values of the variable. It helps to be very familiar with the identities or to have a list of them accessible while working the problems. Reviewing the general rules presented earlier may help simplify the process of verifying an identity.

How to: Given an identity, verify using sum and difference formulas

1. Begin with the expression on the side of the equal sign that appears most complex. Rewrite that expression until it matches the other side of the equal sign. Occasionally, we might have to alter both sides, but working on only one side is the most efficient.
2. Look for opportunities to use the sum and difference formulas.
3. Rewrite sums or differences of quotients as single quotients.
4. If the process becomes cumbersome, rewrite the expression in terms of sines and cosines.

Example $\PageIndex{8A}$: Verifying an Identity Involving Sine

Verify the identity $\sin(\alpha+\beta)+\sin(\alpha−\beta)=2\sin \alpha \cos \beta$.

Solution

We see that the left side of the equation includes the sines of the sum and the difference of angles.

$\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta$

$\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta$

We can rewrite each using the sum and difference formulas.

$$\begin{align*} \sin(\alpha+\beta)+\sin(\alpha-\beta)&= \sin \alpha \cos \beta+\cos \alpha \sin \beta+\sin \alpha \cos \beta-\cos \alpha \sin \beta\\[4pt] &= 2\sin \alpha \cos \beta \end{align*}$$

We see that the identity is verified.

Example $\PageIndex{8B}$: Verifying an Identity Involving Tangent

Verify the following identity.

$\dfrac{\sin(\alpha−\beta)}{\cos \alpha \cos \beta}=\tan \alpha−\tan \beta$

Solution

We can begin by rewriting the numerator on the left side of the equation.

$$\begin{align*} \dfrac{\sin(\alpha-\beta)}{\cos \alpha \cos \beta}&= \dfrac{\sin \alpha \cos \beta-\cos \alpha \sin \beta}{\cos \alpha \cos \beta}\\[4pt] &= \dfrac{\sin \alpha \cos \beta}{\cos \alpha \cos \beta}-\dfrac{\cos \alpha \sin \beta}{\cos \alpha \cos \beta} & & \text{Rewrite using a common denominator}\\[4pt] &= \dfrac{\sin \alpha}{\cos \alpha}-\dfrac{\sin \beta}{\cos \beta} & & \text{Cancel}\\[4pt] &= \tan \alpha-\tan \beta & & \text{Rewrite in terms of tangent} \end{align*}$$

Exercise $\PageIndex{8}$:

Verify the identity: $\tan(\pi−\theta)=−\tan \theta$.

Answer

$$\begin{align*} \tan(\pi-\theta)&= \dfrac{\tan(\pi)-\tan \theta}{1+\tan(\pi)\tan \theta}\\[4pt] &= \dfrac{0-\tan \theta}{1+0\cdot \tan \theta}\\[4pt] &= -\tan \theta \end{align*}$$

Example $\PageIndex{9A}$: Using Sum and Difference Formulas to Solve an Application Problem

Let $L_1$ and $L_2$ denote two non-vertical intersecting lines, and let $θ$ denote the acute angle between $L_1$ and $L_2$. See Figure $\PageIndex{7}$. Show that

$\tan \theta=\dfrac{m_2-m_1}{1+m_1m_2}$

where $m_1$ and $m_2$ are the slopes of $L_1$ and $L_2$ respectively. (Hint: Use the fact that $\tan \theta_1=m_1$ and $\tan \theta_2=m_2$.)

Figure $\PageIndex{7}$

Solution

Using the difference formula for tangent, this problem does not seem as daunting as it might.

$$\begin{align*} \tan \theta&= \tan(\theta_2-\theta_1)\\[4pt] &= \dfrac{\tan \theta_2-\tan \theta_1}{1+\tan \theta_1 \tan \theta_2}\\[4pt] &= \dfrac{m_2-m_1}{1+m_1m_2} \end{align*}$$

Example $\PageIndex{9B}$: Investigating a Guy-wire Problem

For a climbing wall, a guy-wire $R$ is attached $47$ feet high on a vertical pole. Added support is provided by another guy-wire $S$ attached $40$ feet above ground on the same pole. If the wires are attached to the ground $50$ feet from the pole, find the angle $\alpha$ between the wires. See Figure $\PageIndex{8}$.

Figure $\PageIndex{8}$

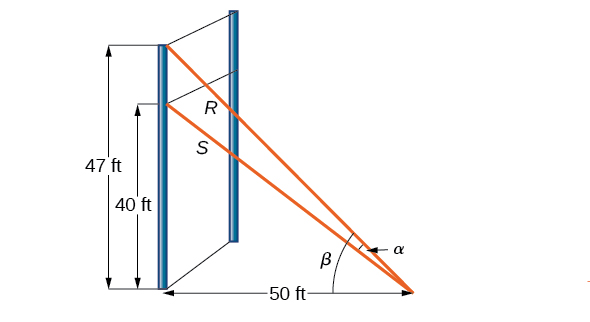
Solution

Let’s first summarize the information we can gather from the diagram. As only the sides adjacent to the right angle are known, we can use the tangent function. Notice that $\tan \beta=\frac{47}{50}$, and $\tan(\beta−\alpha)=\frac{40}{50}=\frac{4}{5}$. We can then use difference formula for tangent.

$$\tan(\beta-\alpha) = \dfrac{\tan \beta-\tan \alpha}{1+\tan \beta \tan \alpha}$$
Now, substituting the values we know into the formula, we have,
$$\begin{align*} \dfrac{4}{5}&= \dfrac{\tfrac{47}{50}-\tan \alpha}{1+\tfrac{47}{50}\tan \alpha}\\[4pt] 4\left(1+\tfrac{47}{50}\tan \alpha\right)&= 5\left(\tfrac{47}{50}-\tan \alpha\right)\end{align*}$$
Use the distributive property, and then simplify the functions.
$$\begin{align*} 4(1)+4\left(\tfrac{47}{50}\right)\tan \alpha &= 5\left(\tfrac{47}{50}\right)-5\tan \alpha\\[4pt] 4+3.76\tan \alpha&= 4.7-5\tan \alpha\\[4pt] 5\tan \alpha+3.76\tan \alpha&= 0.7\\[4pt] 8.76 \tan \alpha&= 0.7\\[4pt] \tan \alpha&\approx 0.07991\\[4pt] \tan^{-1}(0.07991)&\approx .079741\end{align*}$$
Now we can calculate the angle in degrees.
$$\begin{align*} \alpha &\approx 0.079741\left(\dfrac{180}{\pi}\right)\\[4pt] &\approx 4.57^{\circ} \end{align*}$$

Analysis

Occasionally, when an application appears that includes a right triangle, we may think that solving is a matter of applying the Pythagorean Theorem. That may be partially true, but it depends on what the problem is asking and what information is given.

Media

Access these online resources for additional instruction and practice with sum and difference identities.

• Sum and Difference Identities for Cosine
• Sum and Difference Identities for Sine
• Sum and Difference Identities for Tangent

Key Equations

Sum Formula for Cosine	$\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta$
Difference Formula for Cosine	$\cos(\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta$
Sum Formula for Sine	$\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta$
Difference Formula for Sine	$\sin(\alpha-\beta)=\sin \alpha \cos \beta-\cos \alpha \sin \beta$
Sum Formula for Tangent	$\tan(\alpha+\beta)=\dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}$
Difference Formula for Tangent	$\tan (\alpha-\beta)=\dfrac{\tan (\alpha)-\tan (\beta)}{1+\tan (\alpha) \tan (\beta)}$
Cofunction identities	$\sin \theta=\cos\left(\dfrac{\pi}{2}-\theta\right)$ $\cos \theta=\sin\left(\dfrac{\pi}{2}-\theta\right)$ $\tan \theta=\cot\left(\dfrac{\pi}{2}-\theta\right)$ $\cot \theta=\tan\left(\dfrac{\pi}{2}-\theta\right)$ $\sec \theta=\csc\left(\dfrac{\pi}{2}-\theta\right)$ $\csc \theta=\sec\left(\dfrac{\pi}{2}-\theta\right)$

Key Concepts

• The sum formula for cosines states that the cosine of the sum of two angles equals the product of the cosines of the angles minus the product of the sines of the angles. The difference formula for cosines states that the cosine of the difference of two angles equals the product of the cosines of the angles plus the product of the sines of the angles.
• The sum and difference formulas can be used to find the exact values of the sine, cosine, or tangent of an angle. See Example $\PageIndex{1}$ and Example $\PageIndex{2}$.
• The sum formula for sines states that the sine of the sum of two angles equals the product of the sine of the first angle and cosine of the second angle plus the product of the cosine of the first angle and the sine of the second angle. The difference formula for sines states that the sine of the difference of two angles equals the product of the sine of the first angle and cosine of the second angle minus the product of the cosine of the first angle and the sine of the second angle. See Example $\PageIndex{3}$.
• The sum and difference formulas for sine and cosine can also be used for inverse trigonometric functions. See Example $\PageIndex{4}$.
• The sum formula for tangent states that the tangent of the sum of two angles equals the sum of the tangents of the angles divided by $1$ minus the product of the tangents of the angles. The difference formula for tangent states that the tangent of the difference of two angles equals the difference of the tangents of the angles divided by $1$ plus the product of the tangents of the angles. See Example $\PageIndex{5}$.
• The Pythagorean Theorem along with the sum and difference formulas can be used to find multiple sums and differences of angles. See Example $\PageIndex{6}$.
• The cofunction identities apply to complementary angles and pairs of reciprocal functions. See Example $\PageIndex{7}$.
• Sum and difference formulas are useful in verifying identities. See Example $\PageIndex{8}$ and Example $\PageIndex{9}$.
• Application problems are often easier to solve by using sum and difference formulas. See Example $\PageIndex{10}$ and Example $\PageIndex{11}$.