1.4: Fractions
- Page ID
- 18329
Learning Objectives
- Reduce a fraction to lowest terms.
- Multiply and divide fractions.
- Add and subtract fractions.
Reducing
A fraction is a real number written as a quotient, or ratio, of two integers \(a\) and \(b\), where \(b \neq 0\).

The integer above the fraction bar is called the numerator and the integer below is called the denominator. The numerator is often called the “part” and the denominator is often called the “whole.” Equivalent fractions are two equal ratios expressed using different numerators and denominators. For example,
\(\frac{50}{100} = \frac{1}{2}\)
Fifty parts out of \(100\) is the same ratio as \(1\) part out of \(2\) and represents the same real number. Consider the following factorizations of \(50\) and \(100\):
\[
\begin{align*}
50 &= 2 \cdot 25 \\
100 &= 4 \cdot 25
\end{align*}
\]
The numbers \(50\) and \(100\) share the factor \(25\). A shared factor is called a common factor. We can rewrite the ratio \(\frac{50}{100}\) as follows:
\(\frac{50}{100} = \frac{2 \cdot 25}{4 \cdot 25}\)
Making use of the multiplicative identity property and the fact that \(\frac{25}{25} = 1\), we have
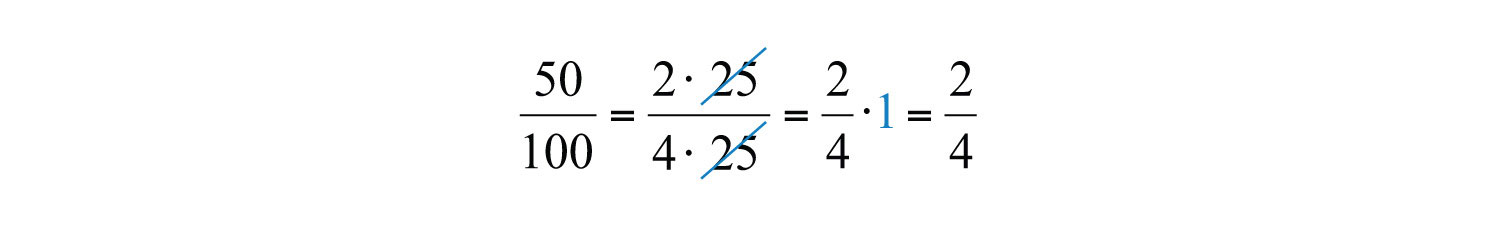
Dividing \(\frac{25}{25}\) and replacing this factor with a \(1\) is called canceling. Together, these basic steps for finding equivalent fractions define the process of reducing. Since factors divide their product evenly, we achieve the same result by dividing both the numerator and denominator by \(25\) as follows:
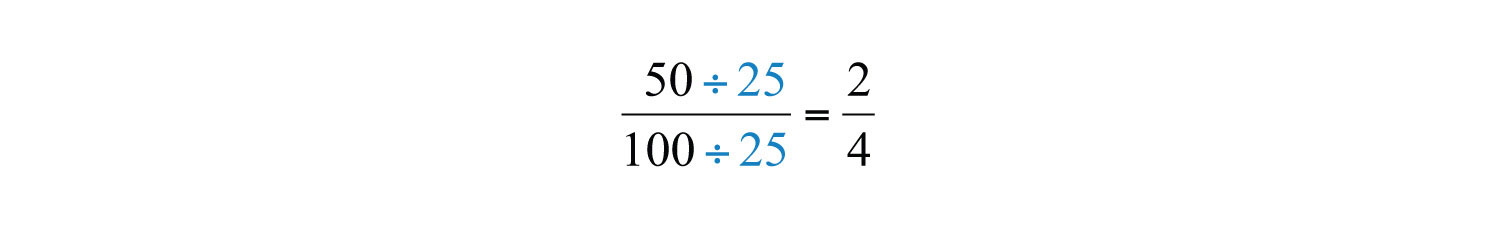
Finding equivalent fractions where the numerator and denominator have no common factor other than \(1\) is called reducing to lowest terms. When learning how to reduce to lowest terms, it is helpful to first rewrite the numerator and denominator as a product of primes and then cancel. For example,
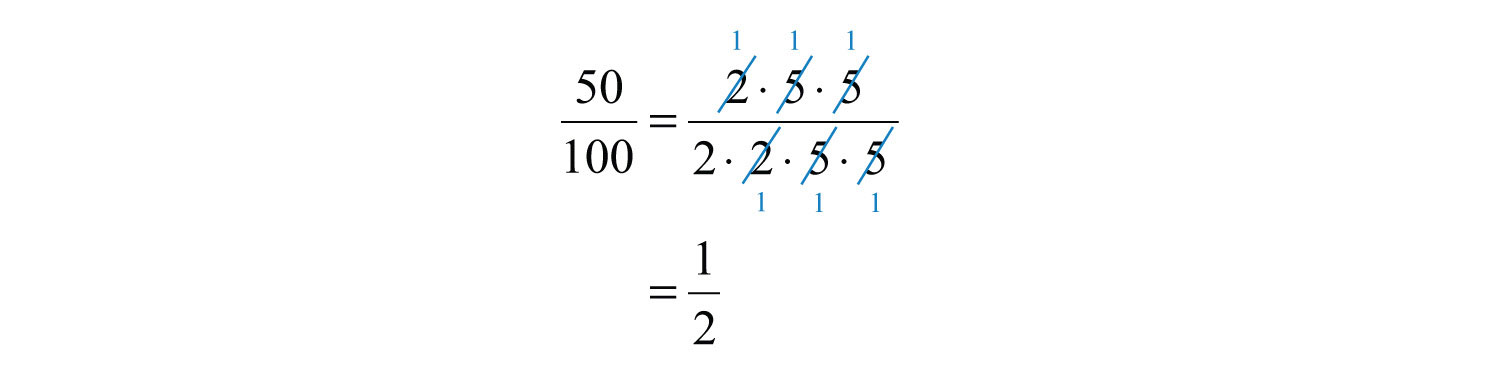
We achieve the same result by dividing the numerator and denominator by the greatest common factor (GCF). The GCF is the largest number that divides both the numerator and denominator evenly. One way to find the GCF of \(50\) and \(100\) is to list all the factors of each and identify the largest number that appears in both lists. Remember, each number is also a factor of itself.
\[
\begin{align*}
&\{1,2,5,10,25,50\} && \color{Cerulean}{Factors\ of\ 50} \\
&\{1,2,4,5,10,20,25,50,100\} && \color{Cerulean}{Factors\ of\ 100}
\end{align*}
\]
Common factors are listed in bold, and we see that the greatest common factor is \(50\). We use the following notation to indicate the GCF of two numbers: GCF\((50, 100) = 50\). After determining the GCF, reduce by dividing both the numerator and the denominator as follows:
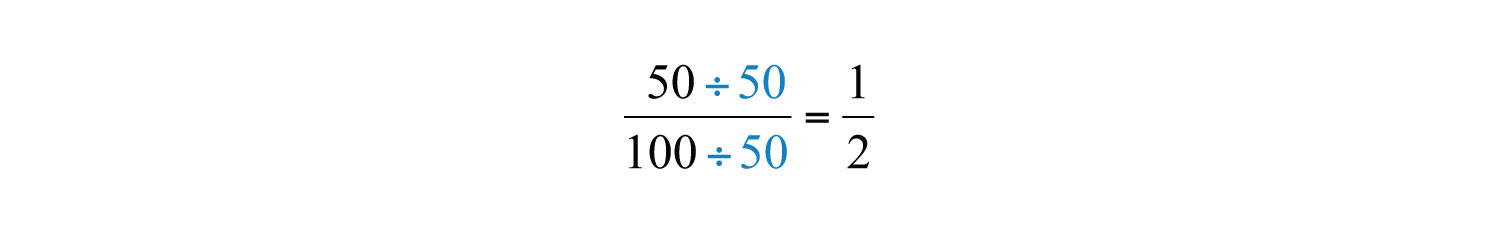
Example \(\PageIndex{1}\)
Reduce to lowest terms: \(\frac{105}{300}\).
Solution
Rewrite the numerator and denominator as a product of primes and then cancel.
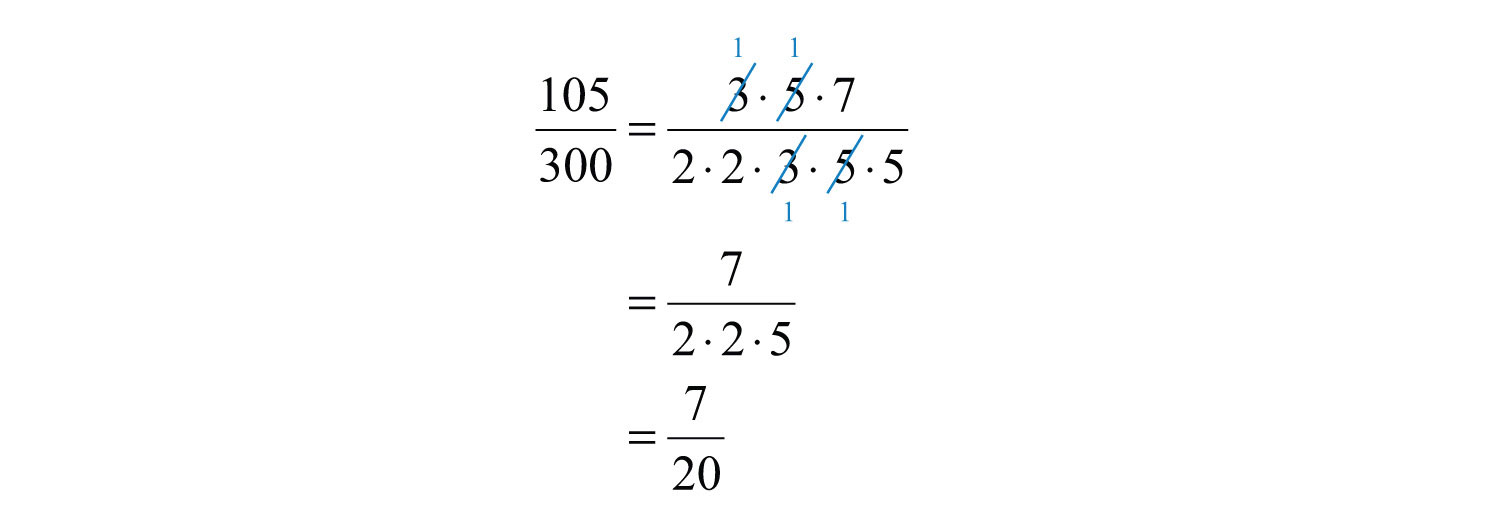
Alternatively, we achieve the same result if we divide both the numerator and denominator by the GCF\((105, 300)\). A quick way to find the GCF of the two numbers requires us to first write each as a product of primes. The GCF is the product of all the common prime factors.
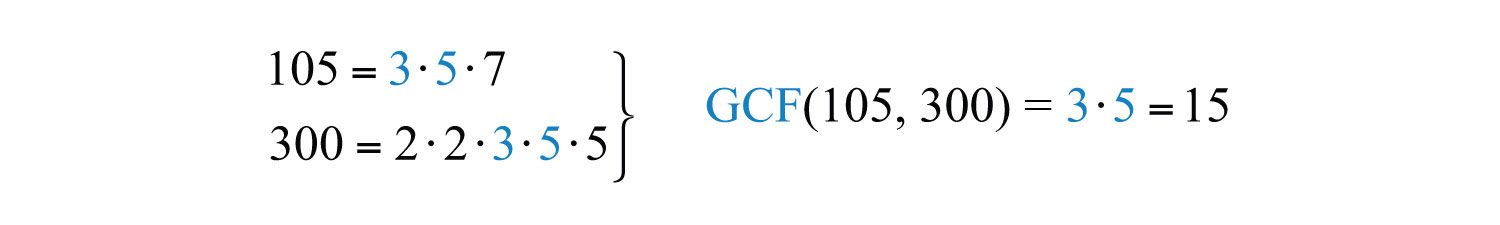
In this case, the common prime factors are \(3\) and \(5\) and the greatest common factor of \(105\) and \(300\) is \(15\).
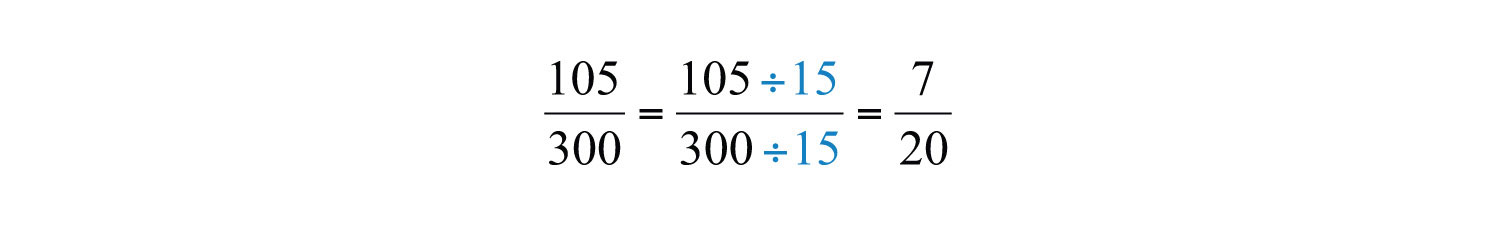
Answer:
\(\frac{7}{20}\)
Example \(\PageIndex{2}\)
Try this! Reduce to lowest terms: \(\frac{32}{96}\).
Video Solution:
(click to see video)
An improper fraction is one where the numerator is larger than the denominator. A mixed number is a number that represents the sum of a whole number and a fraction. For example, \(5 \frac{1}{2}\) is a mixed number that represents the sum \(5+\frac{1}{2}\). Use long division to convert an improper fraction to a mixed number; the remainder is the numerator of the fractional part.
Example \(\PageIndex{3}\)
Write \(\frac{23}{5}\) as a mixed number.
Solution
Notice that \(5\) divides into \(23\) four times with a remainder of \(3\).
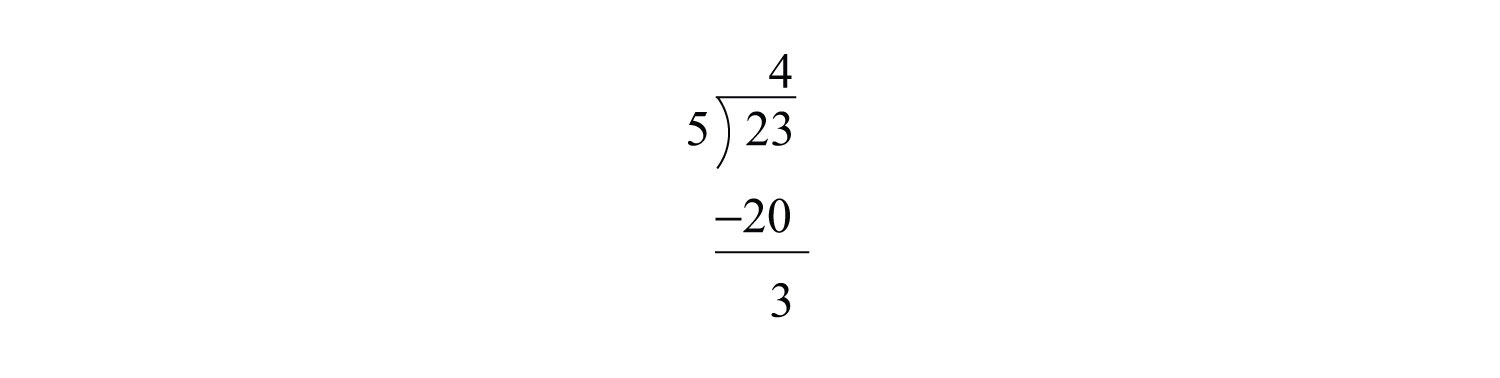
We then can write
\[
\begin{align*}
\frac{23}{5} &= 4 + \frac{3}{5} \\
&= 4 \frac{3}{5}
\end{align*}
\]
Note that the denominator of the fractional part of the mixed number remains the same as the denominator of the original fraction.
Answer
\(4 \frac{3}{5}\)
To convert mixed numbers to improper fractions, multiply the whole number by the denominator and then add the numerator; write this result over the original denominator.
Example \(\PageIndex{4}\)
Write \(3 \frac{5}{7}\) as an improper fraction.
Solution
Obtain the numerator by multiplying \(7\) times \(3\) and then add \(5\).
\[
\begin{align*}
3 \frac{5}{7} &= \frac{7 \cdot 3 + 5}{7} \\
&= \frac{21+5}{7} \\
&= \frac{26}{7}
\end{align*}
\]
Answer
\(\frac{26}{7}\)
It is important to note that converting to a mixed number is not part of the reducing process. We consider improper fractions, such as \(267\), to be reduced to lowest terms. In algebra it is often preferable to work with improper fractions, although in some applications, mixed numbers are more appropriate.
Example \(\PageIndex{5}\)
Try this! Convert \(10 \frac{1}{2}\) to an improper fraction.
Solution
(click to see video)
Multiplying and Dividing Fractions
In this section, assume that \(a, b, c\), and \(d\) are all nonzero integers. The product of two fractions is the fraction formed by the product of the numerators and the product of the denominators. In other words, to multiply fractions, multiply the numerators and multiply the denominators:
\(\frac{a}{b} \cdot \frac{c}{d} = \frac{ac}{bd}\)
Example \(\PageIndex{6}\)
Multiply: \(\frac{2}{3} \cdot \frac{5}{7}\)
Solution
Multiply the numerators and multiply the denominators.
\[
\begin{align*}
\frac{2}{3} \cdot \frac{5}{7} &= \frac{2 \cdot 5}{3 \cdot 7} \\
&= \frac{10}{21}
\end{align*}
\]
Answer:
\(\frac{10}{21}\)
Example \(\PageIndex{7}\)
Multiply: \(\frac{5}{9}\left(-\frac{1}{4}\right)\)
Solution
Recall that the product of a positive number and a negative number is negative.
\[
\begin{align*}
\frac{5}{9}\left(-\frac{1}{4}\right) &= -\frac{5 \cdot 1}{9 \cdot 4} \\
&= -\frac{5}{36}
\end{align*}
\]
Answer:
\(-\frac{5}{36}\)
Example \(\PageIndex{8}\)
Multiply: \(\frac{2}{3} \cdot 5 \frac{3}{4}\)
Solution
Begin by converting \(5 \frac{3}{4}\) to an improper fraction.
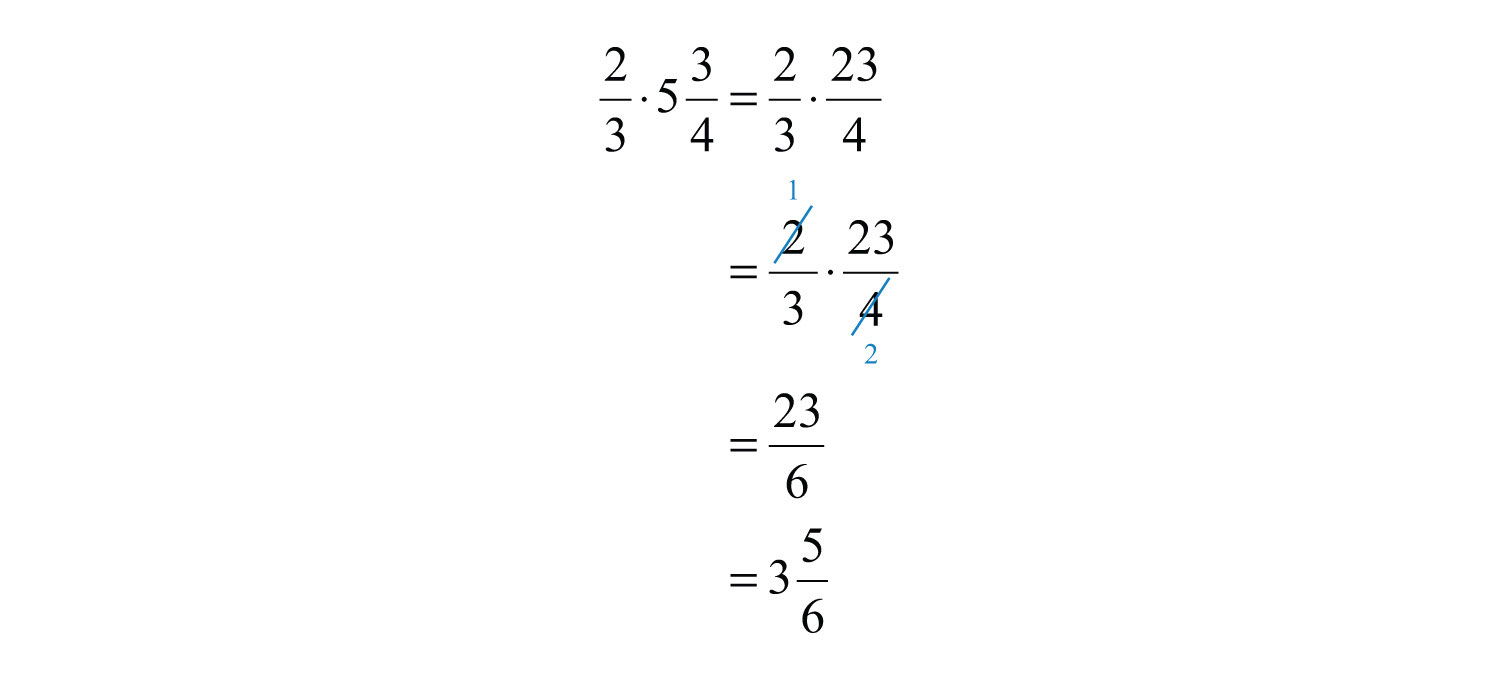
In this example, we noticed that we could reduce before we multiplied the numerators and the denominators. Reducing in this way is called cross canceling, and can save time when multiplying fractions.
Answer
\(3 \frac{5}{6}\)
Two real numbers whose product is \(1\) are called reciprocals. Therefore, \(\frac{a}{b}\) and \(\frac{b}{a}\) are reciprocals because \( \frac{a}{b} \cdot \frac{b}{a} = \frac{ab}{ab} = 1\). For example,
\(\frac{2}{3} \cdot \frac{3}{2} = \frac{6}{6} = 1\)
Because their product is \(1\), \(\frac{2}{3}\) and \(\frac{3}{2}\) are reciprocals. Some other reciprocals are listed below:
\(\frac{5}{8}\ \text{and}\ \frac{8}{5} \qquad 7\ \text{and}\ \frac{1}{7} \qquad -\frac{4}{5}\ \text{and}\ -\frac{5}{4}\)
This definition is important because dividing fractions requires that you multiply the dividend by the reciprocal of the divisor.
\(\frac{a}{b} \div \color{Cerulean}{\frac{c}{d}} \color{Black}{=} \frac{a}{b} \cdot \color{Cerulean}{\frac{d}{c}} \color{Black}{=} \frac{ad}{bc} \)
Example \(\PageIndex{9}\)
Divide: \(\frac{2}{3} \div \frac{5}{7}\)
Solution
Multiply \(\frac{2}{3}\) by the reciprocal of \(\frac{5}{7}\).
\[
\begin{align*}
\frac{2}{3} \div \frac{5}{7} &= \frac{2}{3} \cdot \frac{7}{5} \\
&= \frac{2 \cdot 7}{3 \cdot 5 } \\
&= \frac{14}{15}
\end{align*}
\]
Answer:
\(\frac{14}{15\)
You also need to be aware of other forms of notation that indicate division: / and —. For example,
\(5/(1/2) = 5*(2/1)=(5/1)*(2/1)= 10/1=10\)
Or
\(\frac{\frac{7}{8}}{\color{Cerulean}{\frac{2}{3}}} \color{Black}{=} \frac{7}{8} \div \color{Cerulean}{\frac{2}{3}} \color{Black}{=} \frac{7}{8} \cdot \color{Cerulean}{\frac{3}{2}} \color{Black}{=} \frac{21}{16}\)
The latter is an example of a complex fraction, which is a fraction whose numerator, denominator, or both are fractions.
Note
Students often ask why dividing is equivalent to multiplying by the reciprocal of the divisor. A mathematical explanation comes from the fact that the product of reciprocals is \(1\). If we apply the multiplicative identity property and multiply numerator and denominator by the reciprocal of the denominator, then we obtain the following:
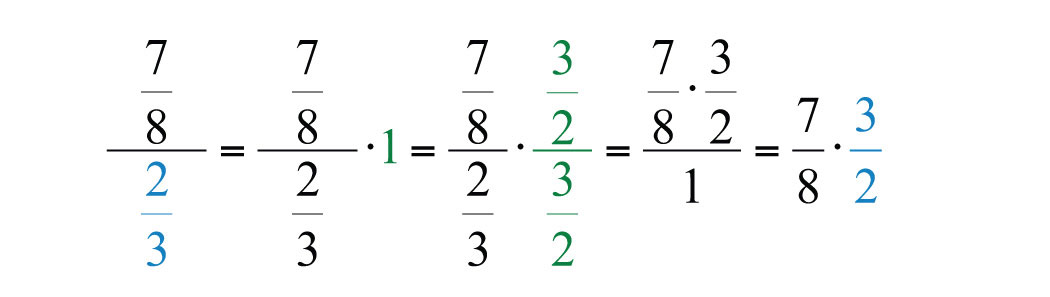
Before multiplying, look for common factors to cancel; this eliminates the need to reduce the end result.
Example \(\PageIndex{10}\)
Divide: \(\frac{\frac{5}{2}}{\frac{7}{4}}\).
Solution
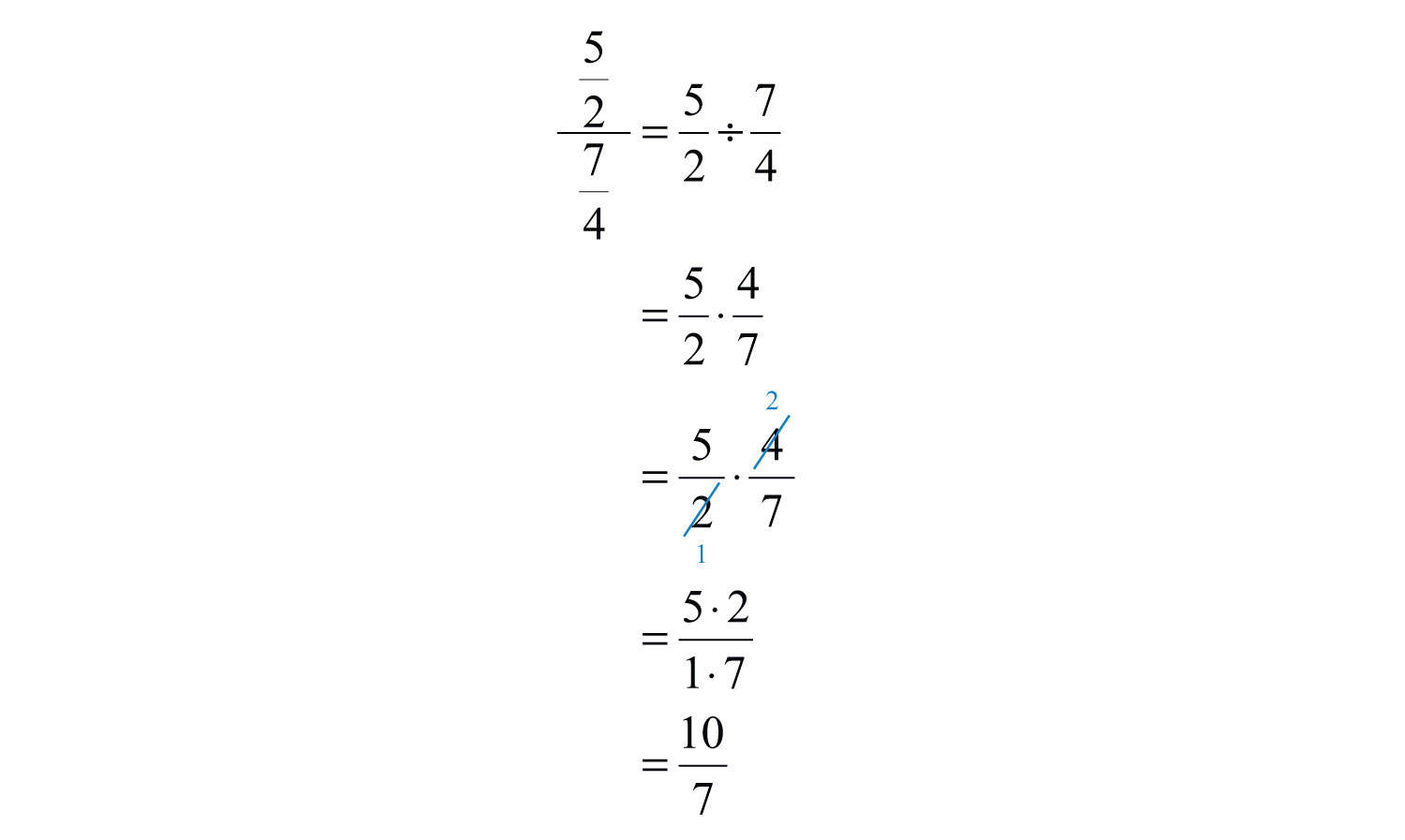
Answer
\(\frac{10}{7}\)
When dividing by an integer, it is helpful to rewrite it as a fraction over \(1\).
Example \(\PageIndex{11}\)
Divide: \(\frac{2}{3} \div 6\)
Solution
Rewrite 6 as \(\frac{6}{1}\) and multiply by its reciprocal.
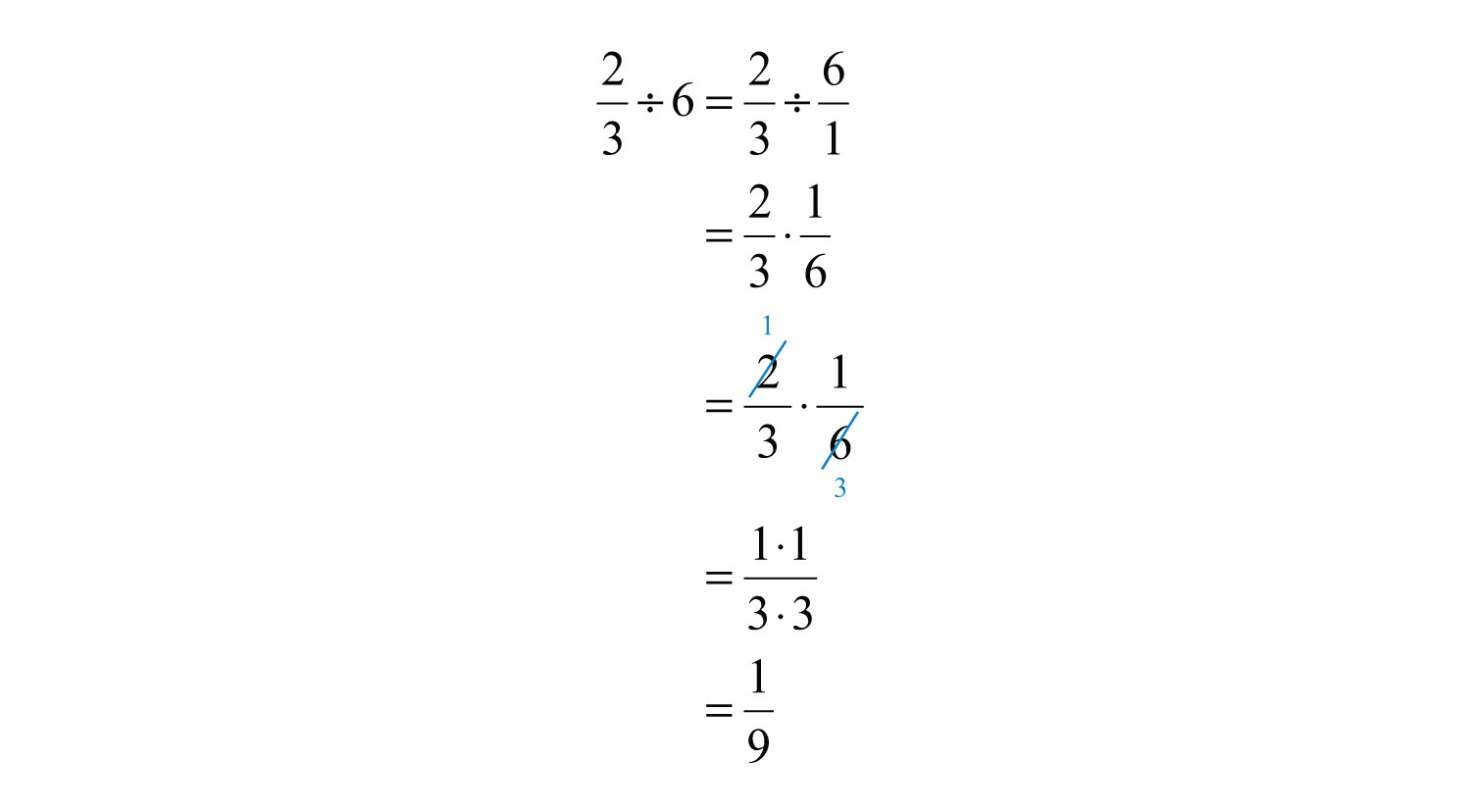
Answer:
\(\frac{1}{9}\)
Also, note that we only cancel when working with multiplication. Rewrite any division problem as a product before canceling.
Example \(\PageIndex{12}\)
Try this! Divide: \(5 \div 2 \frac{3}{5} \)
Video Solution:
(click to see video)
Adding and Subtracting Fractions
Negative fractions are indicated with the negative sign in front of the fraction bar, in the numerator, or in the denominator. All such forms are equivalent and interchangeable.
\(\frac{-3}{4} = -\frac{3}{4} = \frac{3}{-4}\)
Adding or subtracting fractions requires a common denominator. In this section, assume the common denominator c is a nonzero integer.
It is good practice to use positive common denominators by expressing negative fractions with negative numerators. In short, avoid negative denominators.
Example \(\PageIndex{13}\)
Subtract: \(\frac{12}{15} - \frac{3}{15}\)
Solution
The two fractions have a common denominator \(15\). Therefore, subtract the numerators and write the result over the common denominator:
\[
\begin{align*}
\frac{12}{15} - \frac{3}{15} &= \frac{12-3}{15} && \color{Cerulean}{Subtract\ the\ numerators.} \\
&= \color{Black}{\frac{9}{15}} \\
&=\frac{9 \color{Cerulean}{\div 3}}{\color{Black}{15} \color{Cerulean}{\div 3}} &&\color{Cerulean}{Reduce.} \\
&= \frac{3}{5}
\end{align*}
\]
Answer
\(\frac{3}{5}\)
Most problems that you are likely to encounter will have unlike denominators. In this case, first find equivalent fractions with a common denominator before adding or subtracting the numerators. One way to obtain equivalent fractions is to divide the numerator and the denominator by the same number. We now review a technique for finding equivalent fractions by multiplying the numerator and the denominator by the same number. It should be clear that \(5/5\) is equal to \(1\) and that \(1\) multiplied times any number is that number:
\(\frac{1}{2} = \frac{1}{2} \cdot \color{Cerulean}{1} \color{Black}{=} \frac{1}{2} \cdot \color{Cerulean}{\frac{5}{5}} \color{Black}{=} \frac{5}{10}\)
We have equivalent fractions \(\frac{1}{2}=\frac{5}{10}\). Use this idea to find equivalent fractions with a common denominator to add or subtract fractions. The steps are outlined in the following example.
Example \(\PageIndex{14}\)
Subtract: \(\frac{7}{15} - \frac{3}{10}\)
Solution
Step 1: Determine a common denominator. To do this, use the least common multiple (LCM) of the given denominators. The LCM of \(15\) and \(10\) is indicated by LCM\((15, 10)\). Try to think of the smallest number that both denominators divide into evenly. List the multiples of each number:

Common multiples are listed in bold, and the least common multiple is \(30\).
LCM\((10,15)=30\)
Step 2: Multiply the numerator and the denominator of each fraction by values that result in equivalent fractions with the determined common denominator.
\[\begin{align*}
\frac{7}{15} - \frac{3}{10} &= \frac{7 \color{Cerulean}{\cdot 2}}{15 \color{Cerulean}{\cdot 3}} - \frac{3\color{Cerulean}{\cdot 3}}{10 \color{Cerulean}{\cdot 3}} \\
&= \frac{14}{30} - \frac{9}{30}
\end{align*}\]
Step 3: Add or subtract the numerators, write the result over the common denominator and then reduce if possible.
\[\begin{align*}
\frac{14}{30} - \frac{9}{30} &= \frac{14-9}{30} \\
&= \frac{5}{30} \\
&= \frac{5 \color{Cerulean}{\div 5}}{30 \color{Cerulean}{\div 5}} \\
&= \frac{1}{6}
\end{align*}\]
Answer:
\(\frac{1}{6}\)
The least common multiple of the denominators is called the least common denominator (LCD). Finding the LCD is often the difficult step. It is worth finding because if any common multiple other than the least is used, then there will be more steps involved when reducing.
Example \(\PageIndex{15}\)
Add: \(\frac{5}{10} + \frac{1}{18}\)
Solution
First, determine that the LCM\((10, 18)\) is \(90\) and then find equivalent fractions with \(90\) as the denominator.
\[\begin{align*}
\frac{5}{10} + \frac{1}{18} &= \frac{5 \color{Cerulean}{\cdot 9}}{10 \color{Cerulean}{\cdot 9}} + \frac{1 \color{Cerulean}{\cdot 5}}{18 \color{Cerulean}{\cdot 5}} \\
&= \frac{45}{90} + \frac{5}{90} \\
&= \frac{45+5}{90} \\
&= \frac{50}{90} \\
&= \frac{50 \color{Cerulean}{\div 10}}{90 \color{Cerulean}{\div 10}} \\
&= \frac{5}{9}
\end{align*}\]
Answer
\(\frac{5}{9}\)
Example \(\PageIndex{16}\)
Try this! Add: \(\frac{2}{30} + \frac{5}{21}\)
Video Solution:
(click to see video)
Example \(\PageIndex{17}\)
Simplify: \(2 \frac{1}{3} + \frac{3}{5} - \frac{1}{2}\)
Solution
Begin by converting \(2 \frac{1}{3}\) to an improper fraction.

Answer:
\(2 \frac{13}{30}\)
In general, it is preferable to work with improper fractions. However, when the original problem involves mixed numbers, if appropriate, present your answers as mixed numbers. Also, mixed numbers are often preferred when working with numbers on a number line and with real-world applications.
Example \(\PageIndex{18}\)
Try this! Subtract: \(\frac{5}{7} - 2 \frac{1}{7}\)
Video Solution:
(click to see video)
Example \(\PageIndex{19}\)
How many \(\frac{1}{2}\) inch thick paperback books can be stacked to fit on a shelf that is \(1 \frac{1}{2}\) feet in height?
Solution
First, determine the height of the shelf in inches. To do this, use the fact that there are \(12\) inches in \(1\) foot and multiply as follows:
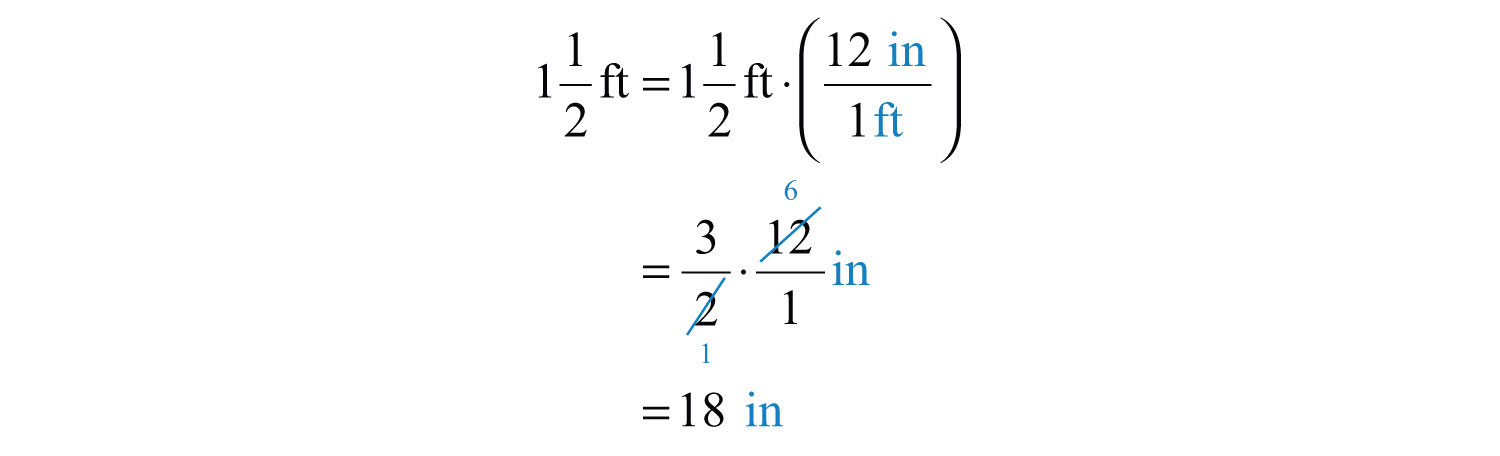
Next, determine how many notebooks will fit by dividing the height of the shelf by the thickness of each book.
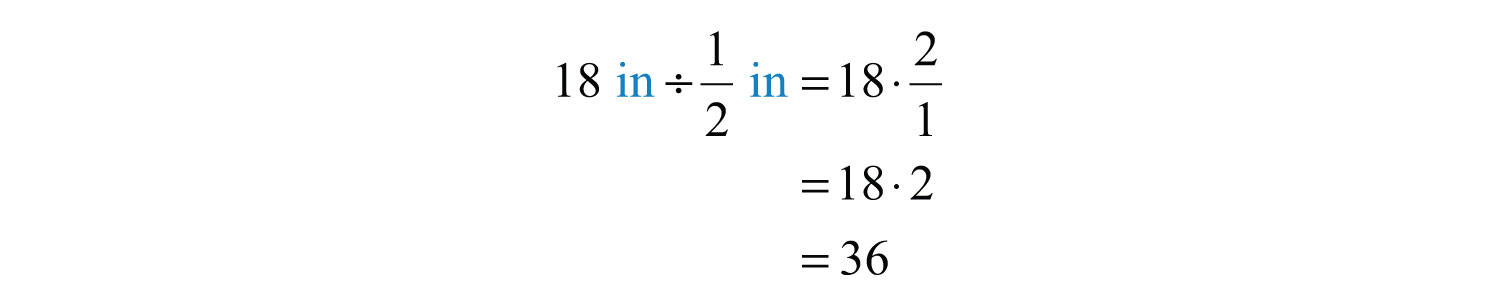
Answer
\(36\) books can be stacked on the shelf.
Key Takeaways:
- Fractions are not unique; there are many ways to express the same ratio. Find equivalent fractions by multiplying or dividing the numerator and the denominator by the same real number.
- Equivalent fractions in lowest terms are generally preferred. It is a good practice to always reduce.
- In algebra, improper fractions are generally preferred. However, in real-life applications, mixed number equivalents are often preferred. We may present answers as improper fractions unless the original question contains mixed numbers, or it is an answer to a real-world or geometric application.
- Multiplying fractions does not require a common denominator; multiply the numerators and multiply the denominators to obtain the product. It is a best practice to cancel any common factors in the numerator and the denominator before multiplying.
- Reciprocals are rational numbers whose product is equal to \(1\). Given a fraction \(\frac{a}{b}\), its reciprocal is \(\frac{b}{a}\).
- Divide fractions by multiplying the dividend by the reciprocal of the divisor. In other words, multiply the numerator by the reciprocal of the denominator.
- Rewrite any division problem as a product before canceling.
- Adding or subtracting fractions requires a common denominator. When the denominators of any number of fractions are the same, simply add or subtract the numerators and write the result over the common denominator.
- Before adding or subtracting fractions, ensure that the denominators are the same by finding equivalent fractions with a common denominator. Multiply the numerator and the denominator of each fraction by the appropriate value to find the equivalent fractions.
- Typically, it is best to convert all mixed numbers to improper fractions before beginning the process of adding, subtracting, multiplying, or dividing.
Exercise \(\PageIndex{1}\)
Reduce each fraction to lowest terms.
1. \(\frac{5}{30}\)
2. \(\frac{6}{24}\)
3. \(\frac{30}{70}\)
4. \(\frac{18}{27}\)
5. \(\frac{44}{84}\)
6. \(\frac{54}{90}\)
7. \(\frac{135}{30}\)
8. \(\frac{105}{300}\)
9. \(\frac{18}{6}\)
10. \(\frac{256}{16}\)
11. \(\frac{126}{45}\)
12. \(\frac{52}{234}\)
13. \(\frac{54}{162}\)
14. \(\frac{2000}{3000}\)
15. \(\frac{270}{360}\)
- Answer
-
1: \(1/6\)
3: \(3/7\)
5: \(11/21\)
7: \(9/2\)
9: \(3\)
11: \(14/5\)
13: \(1/3\)
15: \(3/4\)
Exercise \(\PageIndex{2}\)
Rewrite as an improper fraction.
- \(4\frac{3}{4}\)
- \(2\frac{1}{2}\)
- \(5\frac{7}{15}\)
- \(1\frac{1}{2}\)
- \(3\frac{5}{8}\)
- \(1\frac{3}{4}\)
- \(−2\frac{1}{2}\)
- \(−1\frac{3}{4}\)
- Answer
-
1: \(5/2\)
3: \(3/2\)
5: \(7/4\)
7: \(−7/4\)
Exercise \(\PageIndex{3}\)
Rewrite as a mixed number.
- \(\frac{15}{2}\)
- \(\frac{9}{2}\)
- \(\frac{40}{13}\)
- \(\frac{103}{25}\)
- \(\frac{73}{10}\)
- \(\frac{−52}{7}\)
- \(\frac{−59}{6}\)
- Answer
-
2: \(4\frac{1}{2}\)
4: \(4\frac{3}{25}\)
6: \(−7\frac{3}{7}\)
Exercise \(\PageIndex{4}\)
Multiply and reduce to lowest terms.
- \(\frac{2}{3}⋅\frac{5}{7}\)
- \(\frac{1}{5}⋅\frac{4}{8}\)
- \(\frac{1}{2}⋅\frac{1}{3}\)
- \(\frac{3}{4}⋅\frac{20}{9}\)
- \(\frac{5}{7}⋅\frac{49}{10}\)
- \(\frac{2}{3}⋅\frac{9}{12}\)
- \(\frac{6}{14}⋅\frac{21}{12}\)
- \(\frac{44}{15}⋅\frac{15}{11}\)
- \(3 \frac{3}{4} \cdot 2 \frac{1}{3}\)
- \(2\frac{7}{10}⋅5\frac{5}{6}\)
- \(\frac{3}{11}(−\frac{5}{2})\)
- \(-\frac{4}{5}(\frac{9}{5})\)
- \((−\frac{9}{5} (−\frac{3}{10}) \)
- \(\frac{6}{7}(−\frac{14}{3})\)
- \((−\frac{9}{12})(−\frac{4}{8})\)
- \(−\frac{3}{8}(−\frac{4}{15})\)
- \(\frac{1}{7}⋅\frac{1}{2}⋅\frac{1}{3}\)
- \(\frac{3}{5}⋅\frac{15}{21}⋅\frac{7}{27}\)
- \(\frac{2}{5}⋅3\frac{1}{8}⋅\frac{4}{5}\)
- \(2\frac{4}{9}⋅\frac{2}{5}⋅2\frac{5}{11}\)
- Answer
-
1: \(10/21\)
3: \(1/6\)
5: \(7/2\)
7: \(3/4\)
9: \(834\)
11: \(−15/22\)
13:\(27/50\)
15: \(3/8\)
17: \(1/42\)
19: \(1\)
Exercise \(\PageIndex{5}\)
Determine the reciprocal of the following numbers.
- \(\frac{1}{2}\)
- \(\frac{8}{5}\)
- \(−\frac{2}{3}\)
- \(−\frac{4}{3}\)
- \(10\)
- \(−4\)
- \(2\frac{1}{3}\)
- \(1\frac{5}{8}\)
- Answer
-
1: \(2\)
3: \(−3/2\)
5: \(1/10\)
7: \(3/7\)
9: \(3/4\)
Exercise \(\PageIndex{6}\)
Divide and reduce to lowest terms.
- \(\frac{1}{2} \div \frac{2}{3}\)
- \(\frac{5}{9} \div \frac{1}{3}\)
- \(\frac{5}{8} \div (−\frac{4}{5})\)
- \((−\frac{2}{5})÷\frac{15}{3}\)
- \(\dfrac{−\frac{6}{7}}{−\frac{6}{7}}\)
- \(\dfrac{−\frac{1}{2}}{\frac{1}{4}}\)
- \(\dfrac{−\frac{10}{3}}{−\frac{5}{20}}\)
- \(\dfrac{\frac{2}{3}}{\frac{9}{2}}\)
- \(\dfrac{\frac{30}{50}}{\frac{5}{3}}\)
- \(\dfrac{\frac{1}{2}}{2}\)
- \(\dfrac{5}{\frac{2}{5}}\)
- \(\dfrac{−6}{\frac{5}{4}}\)
- \(2 \frac{1}{2} \div \frac{5}{3}\)
- \(4 \frac{2}{3} \div 3 \frac{1}{2}\)
- \(5 \div 2\frac{3}{5}\)
- \(4\frac{3}{5} \div 23\)
- Answer
-
1: \(3/4\)
3: \(−25/32\)
5: \(1\)
7: \(40/3\)
9: \(9/25\)
11: \(25/2\)
13: \(1 \frac{1}{2}\)
15: \(1 \frac{12}{13}\)
Exercise \(\PageIndex{7}\)
Add or subtract and reduce to lowest terms.
- \(\frac{17}{20}-\frac{5}{20}\)
- \(\frac{4}{9}-\frac{13}{9}\)
- \(\frac{3}{5}+\frac{1}{5}\)
- \(\frac{11}{15}+\frac{9}{15}\)
- \(\frac{5}{7}-2\frac{1}{7}\)
- \(\frac{1}{2}+\frac{1}{3}\)
- \(\frac{1}{5}-\frac{1}{4}\)
- \(\frac{3}{4}-\frac{5}{2}\)
- \(\frac{3}{8}+\frac{7}{16}\)
- \(\frac{7}{15}-\frac{3}{10}\)
- \(\frac{3}{10}+\frac{2}{14}\)
- \(\frac{2}{30}+\frac{5}{21}\)
- \(\frac{3}{18}-\frac{1}{24}\)
- \(5 \frac{1}{2}+2\frac{1}{3}\)
- \(1 \frac{3}{4}+2 \frac{1}{10}\)
- \(\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\)
- \(\frac{2}{3}+\frac{3}{5}-\frac{2}{9}\)
- \(\frac{7}{3}-\frac{3}{2}+\frac{2}{15}\)
- \(\frac{9}{4}-\frac{3}{2}+\frac{3}{8}\)
- \(\frac{2}{3}-4\frac{1}{2}+3\frac{1}{6}\)
- \(1-\frac{6}{16}+\frac{3}{18}\)
- \(3-\frac{1}{21}-\frac{1}{15}\)
- Answer
-
1: \(3/5\)
3: \(4/5\)
5: \(−1 \frac{3}{7}\)
7: \(5/6\)
9: \(−7/4\)
11: \(1/6\)
13: \(32/105\)
15: \(7 \frac{5}{6}\)
17: \(1\)
19: \(29/30\)
21: \(2 \frac{2}{3}\)
23: \(19/24\)
Exercise \(\PageIndex{8}\)
Perform the operations. Reduce answers to lowest terms.
- \(\frac{3}{14} \cdot \frac{7}{3} \div \frac{1}{8}\)
- \(\frac{1}{2} \cdot (-\frac{4}{5}) \div \frac{14}{15}\)
- \(\frac{1}{2} \div \frac{3}{4} \cdot \frac{1}{5}\)
- \(-\frac{5}{9} \div \frac{5}{3} \cdot \frac{5}{2}\)
- \(\frac{4}{5} \div 4 \cdot \frac{1}{2}\)
- \(\frac{5}{3} \div 15 \cdot \frac{2}{3}\)
- What is the product of \(\frac{3}{16}\) and \(\frac{4}{9}\)?
- What is the product of \(−\frac{24}{5}\) and \(\frac{25}{8}\)?
- What is the quotient of \(\frac{5}{9}\) and \(\frac{25}{3}\)?
- What is the quotient of \(−\frac{16}{5}\) and \(32\)?
- Subtract \(\frac{1}{6}\) from the sum of \(\frac{9}{2}\) and \(\frac{2}{3}\).
- Subtract \(\frac{1}{4}\) from the sum of \(\frac{3}{4}\) and \(\frac{6}{5}\).
- What is the total width when \(3\) boards, each with a width of \(2 \frac{5}{8}\) inches, are glued together?
- The precipitation in inches for a particular 3-day weekend was published as \(\frac{3}{10}\) inches on Friday, \(1\frac{1}{2}\) inches on Saturday, and \(\frac{3}{4}\) inches on Sunday. Calculate the total precipitation over this period.
- A board that is \(5\frac{1}{4}\) feet long is to be cut into \(7\) pieces of equal length. What is length of each piece?
- How many \(\frac{3}{4}\) inch thick notebooks can be stacked into a box that is \(2\) feet high?
- In a mathematics class of \(44\) students, one-quarter of the students signed up for a special Saturday study session. How many students signed up?
- Determine the length of fencing needed to enclose a rectangular pen with dimensions \(35\frac{1}{2}\) feet by \(20\frac{2}{3}\) feet.
- Each lap around the track measures \(\frac{1}{4}\) mile. How many laps are required to complete a \(2\frac{1}{2}\) mile run?
- A retiree earned a pension that consists of three-fourths of his regular monthly salary. If his regular monthly salary was \($5,200\), then what monthly payment can the retiree expect from the pension plan?
- Answer
-
1: \(4\)
3: \(2/15\)
5: \(9/28\)
7: \(1/10\)
9: \(1/12\)
11: \(1/15\)
13: \(5\)
15: \(7 \frac{7}{8}\) inches
17: \(\frac{3}{4}\) feet
19: \(11\) students
21: \(10\) laps
Exercise \(\PageIndex{1}\)
Discussion Board Topics
- Does \(0\) have a reciprocal? Explain.
- Explain the difference between the LCM and the GCF. Give an example.
- Explain the difference between the LCM and LCD.
- Why is it necessary to find an LCD in order to add or subtract fractions?
- Explain how to determine which fraction is larger, \(\frac{7}{16}\) or \(\frac{1}{2}\).


