1.6: Exponents and Square Roots

Last updated
Save as PDF

Page ID: 24442

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Learning Objectives

Interpret exponential notation with positive integer exponents.
Calculate the $n$th power of a real number.
Calculate the exact and approximate value of the square root of a real number.

Exponential Notation and Positive Integer Exponents

If a number is repeated as a factor numerous times, then we can write the product in a more compact form using exponential notation. For example,

$5\cdot 5\cdot 5\cdot 5=5^{4}$

The base is the factor, and the positive integer exponent indicates the number of times the base is repeated as a factor. In the above example, the base is $5$ and the exponent is $4$. In general, if $a$ is the base that is repeated as a factor $n$ times, then

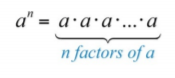$Screenshot (971).png$

Figure $\PageIndex{1}$

When the exponent is $2$, we call the result a square. For example,

$3^{2}=3\cdot 3=9$

The number $3$ is the base and the integer $2$ is the exponent. The notation $3^{2}$ can be read two ways: “three squared” or “$3$ raised to the second power.” The base can be any real number.

It is important to study the difference between the ways the last two examples are calculated. In the example $(−7)^{2}$, the base is $−7$ as indicated by the parentheses. In the example $−5^{2}$, the base is $5$, not $−5$, so only the $5$ is squared and the result remains negative. To illustrate this, write

$-5^{2}=-1\cdot 5^{2}=-1\cdot 5\cdot 5=-25$

This subtle distinction is very important because it determines the sign of the result.

The textual notation for exponents is usually denoted using the caret $(^)$ symbol as follows:

$\begin{aligned}8^{2}&=8\wedge 2=8*8=64 \\ -5.1^{2}&=-5.1\wedge 2=-5.1*5.1=-26.01 \end{aligned}$

The square of an integer is called a perfect square. The ability to recognize perfect squares is useful in our study of algebra. The squares of the integers from $1$ to $15$ should be memorized. A partial list of perfect squares follows:

$\{0,1,4,9,16,25,36,49,64,81,100,121,144,169,196,225,...\}$

Exercise $\PageIndex{1}$

Simplify

$(−12)^{2}$.

Answer: $144$

When the exponent is $3$ we call the result a cube. For example,

$3^{3}=3\cdot 3\cdot 3=27$

The notation $3^{3}$ can be read two ways: “three cubed” or “$3$ raised to the third power.” As before, the base can be any real number.

Note that the result of cubing a negative number is negative. The cube of an integer is called a perfect cube. The ability to recognize perfect cubes is useful in our study of algebra. The cubes of the integers from $1$ to $10$ should be memorized. A partial list of perfect cubes follows:

$\{0,1,8,27,64,125,216,343,512,729,1000,...\}$

Exercise $\PageIndex{2}$

Simplify $(−2)^{3}$.

Answer: $-8$

If the exponent is greater than $3$, then the notation an is read “a raised to the $n$th power.”

$\begin{aligned} 10^{6}&=10\cdot 10\cdot 10\cdot 10\cdot 10\cdot 10=1,000,000 \\ (-1)^{4}&=(-1)(-1)(-1)(-1)=1 \\ \left(\frac{1}{3} \right)^{5}&=\frac{1}{3}\cdot \frac{1}{3}\cdot \frac{1}{3}\cdot \frac{1}{3}\cdot \frac{1}{3} =\frac{1}{243} \end{aligned}$

Notice that the result of a negative base with an even exponent is positive. The result of a negative base with an odd exponent is negative. These facts are often confused when negative numbers are involved. Study the following four examples carefully:

Table $\PageIndex{1}$
The base is $(-2)$	The base is $2$
$\begin{array}{c}{(-2)^{4}=(-2)\cdot (-2)\cdot (-2)\cdot (-2)=+16} \\ {(-2)^{3}=(-2)\cdot (-2)\cdot (-2)=-8} \end{array}$	$\begin{array}{c}{-2^{4}=-2\cdot 2\cdot 2\cdot 2=-16}\\{-2^{3}=-2\cdot 2\cdot 2=-8} \end{array}$

The parentheses indicate that the negative number is to be used as the base.

Example $\PageIndex{1}$

Calculate:

$\left(-\frac{1}{3} \right)^{3}$
$\left(-\frac{1}{3} \right)^{4}$

Solution:

The base is $−\frac{1}{3}$ for both problems.

a. Use the base as a factor three times.

$\begin{aligned} \left(-\frac{1}{3} \right)^{3}&=\left(-\frac{1}{3} \right)\left(-\frac{1}{3} \right)\left(-\frac{1}{3} \right) \\ &=-\frac{1}{27} \end{aligned}$

b. Use the base as a factor four times.

$\begin{aligned} \left(-\frac{1}{3} \right)^{4}&=\left(-\frac{1}{3} \right)\left(-\frac{1}{3} \right)\left(-\frac{1}{3} \right)\left(-\frac{1}{3} \right) \\ &=+\frac{1}{81} \end{aligned}$

Answer:

a. $-\frac{1}{27}$; b. $\frac{1}{81}$

Exercise $\PageIndex{3}$

Simplify:

$−10^{4}$ and $(−10)^{4}$.

Answer: $−10,000$ and $10,000$

Square Root of a Real Number

Think of finding the square root of a number as the inverse of squaring a number. In other words, to determine the square root of $25$ the question is, “What number squared equals $25$?” Actually, there are two answers to this question, $5$ and $−5$.

$5^{2}=25\quad\text{and}(-5)^{2}=25$

When asked for the square root of a number, we implicitly mean the principal (nonnegative) square root. Therefore we have,

$\sqrt{a^{2}}=a$, if $a\geq 0$ or more generally $\sqrt{a^{2}}=|a|$

As an example, $\sqrt{25}=5$, which is read “square root of $25$ equals $5$.” The symbol $√$ is called the radical sign and $25$ is called the radicand. The alternative textual notation for square roots follows:

$\sqrt{16}=text{sqrt}(16)=4$

It is also worthwhile to note that

$\sqrt{1}=1\quad\text{and}\quad\sqrt{0}=0$

This is the case because $1^{2}=1$ and $0^{2}=0$.

Example $\PageIndex{2}$

Simplify:

$\sqrt{10,000}$.

Solution:

$10,000$ is a perfect square because $100⋅100=10,000$.

$\begin{aligned} \sqrt{10,000}&=\sqrt{(100)^{2}} \\ &=100 \end{aligned}$

Answer:

$100$

Example $\PageIndex{3}$

Simplify:

$\sqrt{\frac{1}{9}}$.

Solution:

Here we notice that $\frac{1}{9}$ is a square because $\frac{1}{3}⋅\frac{1}{3}=\frac{1}{9}$.

$\begin{aligned} \sqrt{\frac{1}{9}}&=\sqrt{\left(\frac{1}{3} \right)^{2}} \\ &=\frac{1}{3} \end{aligned}$

Answer:

$\frac{1}{3}$

Given $a$ and $b$ as positive real numbers, use the following property to simplify square roots whose radicands are not squares:

$\sqrt{a\cdot b}=\sqrt{a}\cdot\sqrt{b}$

The idea is to identify the largest square factor of the radicand and then apply the property shown above. As an example, to simplify $\sqrt{8}$ notice that $8$ is not a perfect square. However, $8=4⋅2$ and thus has a perfect square factor other than $1$. Apply the property as follows:

$\begin{aligned} \sqrt{8}&=\sqrt{4\cdot 2} \\ &=\color{Cerulean}{\sqrt{4}}\color{black}{\cdot\sqrt{2}} \\ &=\color{Cerulean}{2}\color{black}{\cdot\sqrt{2}}\\&=2\sqrt{2} \end{aligned}$

Here $2\sqrt{2}$ is a simplified irrational number. You are often asked to find an approximate answer rounded off to a certain decimal place. In that case, use a calculator to find the decimal approximation using either the original problem or the simplified equivalent.

$\sqrt{8}=2\sqrt{2}\approx 2.83$

On a calculator, try $2.83\wedge 2$. What do you expect? Why is the answer not what you would expect?

It is important to mention that the radicand must be positive. For example, $\sqrt{−9}$ is undefined since there is no real number that when squared is negative. Try taking the square root of a negative number on your calculator. What does it say?

Note

Taking the square root of a negative number is defined later in the course.

Example $\PageIndex{4}$

Simplify and give an approximate answer rounded to the nearest hundredth:

$\sqrt{75}$.

Solution:

The radicand $75$ can be factored as $25 ⋅ 3$ where the factor $25$ is a perfect square.

$\begin{aligned} \sqrt{75}&=\sqrt{25\cdot 3}&\color{Cerulean}{The\:largest\:perfect\:square} \\ &=\color{Cerulean}{\sqrt{25}}\color{black}{\cdot\sqrt{3}}&\color{Cerulean}{factor\:of\:75\:is\:25.} \\ &=\color{Cerulean}{5}\color{black}{\cdot\sqrt{3}} \\ &=5\sqrt{3} &\color{Cerulean}{Exact\:answer} \\ &\approx 8.66 &\color{Cerulean}{Approximate\:answer} \end{aligned}$

Answer:

$\sqrt{75}\approx 8.66$

As a check, calculate (\sqrt{75}\) and $5\sqrt{3}$ on a calculator and verify that the both results are approximately $8.66$.

Example $\PageIndex{5}$

Simplify:

$\sqrt{180}$.

Solution:

$\begin{aligned} \sqrt{180}&=\sqrt{36\cdot 5} \\ &=\color{Cerulean}{\sqrt{36}}\color{black}{\cdot\sqrt{5}} \\ &=\color{Cerulean}{6}\color{black}{\cdot\sqrt{5}} \\ &=6\sqrt{5} \end{aligned}$

Since the question did not ask for an approximate answer, we present the exact answer.

Answer:

$6\sqrt{5}$

Example $\PageIndex{6}$

Simplify:

$-5\sqrt{162}$.

Solution:

$\begin{aligned} -5\sqrt{162}&=-5\cdot\sqrt{81\cdot 2} \\ &=-5\cdot\color{Cerulean}{\sqrt{81}}\color{black}{\cdot\sqrt{2}} \\ &=-5\cdot\color{Cerulean}{9}\color{black}{\cdot\sqrt{2}} \\ &=-45\cdot\sqrt{2} \\ &=-45\sqrt{2} \end{aligned}$

Answer:

$-45\sqrt{2}$

Exercise $\PageIndex{4}$

Simplify and give an approximate answer rounded to the nearest hundredth:

$\sqrt{128}$.

Answer: $8\sqrt{2}≈11.31$

A right triangle is a triangle where one of the angles measures $90°$. The side opposite the right angle is the longest side, called the hypotenuse, and the other two sides are called legs. Numerous real-world applications involve this geometric figure. The Pythagorean theorem states that given any right triangle with legs measuring $a$ and $b$ units, the square of the measure of the hypotenuse c is equal to the sum of the squares of the measures of the legs: $a^{2}+b^{2}=c^{2}$. In other words, the hypotenuse of any right triangle is equal to the square root of the sum of the squares of its legs.

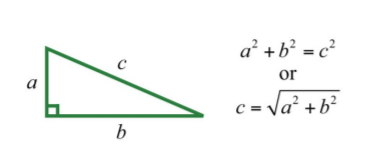$Screenshot (973).png$

Figure $\PageIndex{1}$

Example $\PageIndex{7}$

If the two legs of a right triangle measure $3$ units and $4$ units, then find the length of the hypotenuse.

Solution:

Given the lengths of the legs of a right triangle, use the formula $c=\sqrt{a^{2}+b^{2}}$ to find the length of the hypotenuse.

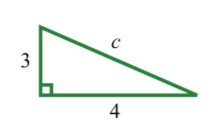$Screenshot (974).png$

Figure $\PageIndex{2}$

$\begin{aligned} c&=\sqrt{a^{2}+b^{2}} \\ c&=\sqrt{3^{2}+4^{2}} \\ &=\sqrt{9+16} \\ &=\sqrt{25} \\ &=5 \end{aligned}$

Answer:

$c=5$ units

When finding the hypotenuse of a right triangle using the Pythagorean theorem, the radicand is not always a perfect square.

Example $\PageIndex{8}$

If the two legs of a right triangle measure $2$ units and $6$ units, find the length of the hypotenuse.

Solution:

$Screenshot (975).png$

Figure $\PageIndex{3}$

$\begin{aligned} c&=\sqrt{a^{2}+b^{2}} \\ &=\sqrt{2^{2}+6^{2}} \\ &=\sqrt{4+36} \\ &=\sqrt{40} \\ &=\sqrt{4\cdot 10} \\&=\sqrt{4}\cdot\sqrt{10} \\ &=2\cdot\sqrt{10} \end{aligned}$

Answer:

$c=2\sqrt{10}$ units

Key Takeaways

When using exponential notation $a^{n}$, the base $a$ is used as a factor $n$ times.
When the exponent is $2$, the result is called a square. When the exponent is $3$, the result is called a cube.
Memorize the squares of the integers up to $15$ and the cubes of the integers up to $10$. They will be used often as you progress in your study of algebra.
When negative numbers are involved, take care to associate the exponent with the correct base. Parentheses group a negative number raised to some power.
A negative base raised to an even power is positive.
A negative base raised to an odd power is negative.
The square root of a number is a number that when squared results in the original number. The principal square root is the positive square root.
Simplify a square root by looking for the largest perfect square factor of the radicand. Once a perfect square is found, apply the property $\sqrt{a⋅b}=\sqrt{a}⋅\sqrt{b}$, where $a$ and $b$ are nonnegative, and simplify.
Check simplified square roots by calculating approximations of the answer using both the original problem and the simplified answer on a calculator to verify that the results are the same.
Find the length of the hypotenuse of any right triangle given the lengths of the legs using the Pythagorean theorem.

Exercise $\PageIndex{5}$ Square of a Number

Simplify.

$10^{2}$
$12^{2}$
$(−9)^{2}$
$−12^{2}$
$11^{2}$
$(−20)^{2}$
$0^{2}$
$1^{2}$
$−(−8)^{2}$
$−(13)^{2}$
$(\frac{1}{2})^{2}$
$(−\frac{2}{3})^{2}$
$0.5^{2}$
$1.25^{2}$
$(−2.6)^{2}$
$−(−5.1)^{2}$
$(2\frac{1}{3})^{2}$
$(5\frac{3}{4})^{2}$

Answer

1. $100$

3. $81$

5. $121$

7. $0$

9. $−64$

11. $\frac{1}{4}$

13. $.25$

15. $6.76$

17. $5\frac{4}{9}$

Exercise $\PageIndex{6}$ Square of a Number

If $s$ is the length of the side of a square, then the area is given by $A=s^{2}$.

Determine the area of a square given that a side measures $5$ inches.
Determine the area of a square given that a side measures $2.3$ feet.
List all the squares of the integers $0$ through $15$.
List all the squares of the integers from $−15$ to $0$.
List the squares of all the rational numbers in the set $\{0, \frac{1}{3}, \frac{2}{3}, 1, \frac{4}{3}, \frac{5}{3}, 2\}$.
List the squares of all the rational numbers in the set $\{0, \frac{1}{2}, 1, \frac{3}{2}, 2, \frac{5}{2}\}$.

Answer

1. $25$ square inches

3. $\{0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121, 144, 169, 196, 225\}$

5. $\{0, \frac{1}{9}, \frac{4}{9}, 1, \frac{16}{9}, \frac{25}{9}, 4\}$

Exercise $\PageIndex{7}$ Integer Exponents

Simplify.

$5^{3}$
$2^{6}$
$(−1)^{4}$
$(−3)^{3}$
$−1^{4}$
$(−2)^{4}$
$−7^{3}$
$(−7)^{3}$
$−(−3)^{3}$
$−(−10)^{4}$
$(−1)^{20}$
$(−1)^{21}$
$(−6)^{3}$
$−3^{4}$
$1^{100}$
$0^{100}$
$−(\frac{1}{2})^{3}$
$(\frac{1}{2})^{6}$
$(\frac{5}{2})^{3}$
$(−\frac{3}{4})^{4}$
List all the cubes of the integers $−5$ through $5$.
List all the cubes of the integers from $−10$ to $0$.
List all the cubes of the rational numbers in the set $\{−\frac{2}{3}, −\frac{1}{3}, 0, \frac{1}{3}, \frac{2}{3}\}$.
List all the cubes of the rational numbers in the set $\{−\frac{3}{7}, −\frac{1}{7}, 0, \frac{1}{7}, \frac{3}{7}\}$.

Answer

1. $125$

3. $1$

5. $−1$

7. $−343$

9. $27$

11. $1$

13. $−216$

15. $1$

17. $−\frac{1}{8}$

19. $\frac{12}{58}$

21. $\{−125, −64, −27, −8, −1, 0, 1, 8, 27, 64, 125\}$

23. $\{−\frac{8}{27}, −\frac{1}{27}, 0, \frac{1}{27}, \frac{8}{27}\}$

Exercise $\PageIndex{8}$ Square Root of a Number

Determine the exact answer in simplified form.

$\sqrt{121}$
$\sqrt{81}$
$\sqrt{100}$
$\sqrt{169}$
$−\sqrt{25}$
$−\sqrt{144}$
$\sqrt{12}$
$\sqrt{27}$
$\sqrt{45}$
$\sqrt{50}$
$\sqrt{98}$
$\sqrt{2000}$
$\sqrt{\frac{1}{4}}$
$\sqrt{\frac{9}{16}}$
$\sqrt{\frac{5}{9}}$
$\sqrt{\frac{8}{36}}$
$\sqrt{0.64}$
$\sqrt{0.81}$
$\sqrt{30^{2}}$
$\sqrt{15^{2}}$
$\sqrt{(−2)^{2}}$
$\sqrt{(−5)^{2}}$
$\sqrt{−9}$
$\sqrt{−16}$
$3\sqrt{16}$
$5\sqrt{18}$
$−2\sqrt{36}$
$−3\sqrt{32}$
$6\sqrt{200}$
$10\sqrt{27}$

Answer

1. $11$

3. $10$

5. $−5$

7. $2\sqrt{3}$

9. $3\sqrt{5}$

11. $7\sqrt{2}$

13. $\frac{1}{2}$

15. $5\sqrt{3}$

17. $0.8$

19. $30$

21. $2$

23. Not real

25. $12$

27. $−12$

29. $60\sqrt{2}$

Exercise $\PageIndex{9}$ Square Root of a Number

Approximate the following to the nearest hundredth.

$\sqrt{2}$
$\sqrt{3}$
$\sqrt{10}$
$\sqrt{15}$
$2\sqrt{3}$
$5\sqrt{2}$
$−6\sqrt{5}$
$-4\sqrt{6}$
$\sqrt{79}$
$\sqrt{54}$
$−\sqrt{162}$
$−\sqrt{86}$
If the two legs of a right triangle measure $6$ units and $8$ units, then find the length of the hypotenuse.
If the two legs of a right triangle measure $5$ units and $12$ units, then find the length of the hypotenuse.
If the two legs of a right triangle measure $9$ units and $12$ units, then find the length of the hypotenuse.
If the two legs of a right triangle measure $\frac{3}{2}$ units and $2$ units, then find the length of the hypotenuse.
If the two legs of a right triangle both measure $1$ unit, then find the length of the hypotenuse.
If the two legs of a right triangle measure $1$ unit and $5$ units, then find the length of the hypotenuse.
If the two legs of a right triangle measure $2$ units and $4$ units, then find the length of the hypotenuse.
If the two legs of a right triangle measure $3$ units and $9$ units, then find the length of the hypotenuse.

Answer

1. $1.41$

3. $3.16$

5. $3.46$

7. $−13.42$

9. $8.89$

11. $−12.73$

13. $10$ units

15. $15$ units

17. $\sqrt{2}$ units

19. $2\sqrt{5}$ units

Exercise $\PageIndex{10}$ Discussion Board Topics

Why is the result of an exponent of $2$ called a square? Why is the result of an exponent of $3$ called a cube?
Research and discuss the history of the Pythagorean theorem.
Research and discuss the history of the square root.
Discuss the importance of the principal square root.

Answer

1. Answers may vary

3. Answers may vary