1.4: Decimal Notation
- Page ID
- 19852
Every rational number can be expressed using decimal notation. To change a fraction into its decimal equivalent, divide the numerator of the fraction by its denominator. In some cases the process will terminate, leaving a zero remainder. However, in other cases, the remainders will begin to repeat, providing a decimal representation that repeats itself in blocks.
Change each of the following fractions into decimals.
- \(\dfrac{39}{80}\)
- \(\dfrac{4}{11}\)
Solution
We perform two divisions, the one on the left to change \(39/80\) to a decimal, the one on the right to find a decimal representation for \(4/11\).

On the left, the division process terminates with a zero remainder. Hence, \(39/80 = 0.4875\) is called a terminating decimal. On the right, the remainders repeat in a pattern and the quotient also repeats in blocks of two. Hence, \(4 / 11=0.3636 \dots\) is called a repeating decimal. We can also use a repeating bar to write \(4 / 11=0 . \overline{36}\). The block under the repeating bar repeats itself indefinitely.
Exercise \(\PageIndex{1}\)
Change \(24 /7\) to a decimal.
- Answer
-
\(3 . \overline{428571}\)
Vice-versa, any terminating decimal can be expressed as a fraction. You need only count the number of digits after the decimal point and use the same number of zeros in your denominator.
Express each of the following decimals as fractions. Reduce your answers to lowest terms.
- \(0.055\)
- \(3.36\)
Solution
In each case, count the number of digits after the decimal point and include an equal number of zeros in the denominator.
- In this example, there are three digits after the decimal point, so we place the number over \(1000\), which has three zeros after the one.\[\begin{aligned} 0.055 &=\dfrac{55}{1000} \\ &=\dfrac{11}{200} \end{aligned} \nonumber \]
- In this example, there are two digits after the decimal point, so we place the number over \(100\), which has two zeros after the one.\[\begin{aligned} 3.36 &=\dfrac{336}{100} \\ &=\dfrac{84}{25} \end{aligned} \nonumber \]
Exercise \(\PageIndex{2}\)
Change \(0.45\) to a fraction. Reduce to lowest terms.
- Answer
-
\(9/20\)
As we saw in Example \(\PageIndex{1}\), the repeating decimal \(0. \overline{36}\) is equivalent to the fraction \(4/11\). Indeed, any repeating decimal can be written as a fraction. For example, \(0. \overline{3}=1 / 3\) and \(0. \overline{142857}=1 / 7\). In future courses you will learn a technique for changing any repeating decimal into an equivalent fraction. However, not all decimals terminate or repeat. For example, consider the decimal \(0.42422422242222 \ldots\), which neither terminates nor repeats. This number cannot be expressed using repeating bar notation because each iteration generates one additional \(2\). Because this number neither repeats nor terminates, it cannot be expressed as a fraction. Hence, \(0.42422422242222 \ldots\) is an example of an irrational number.
Irrational numbers
If a number cannot be expressed in the form \(p/q\), where \(p\) and \(q\) are integers, \(q \neq 0\), then the number is called an irrational number.
Real numbers
By including all of the rational and irrational numbers in one set, we form what is known as the set of real numbers.
The set of real numbers includes every single number we will use in this textbook and course.
Adding and Subtracting Decimals
When adding signed decimals, use the same rules you learned to use when adding signed integers or fractions.
Sign rules for addition
When adding two decimal numbers, use the following rules:
- To add two decimals with like signs, add their magnitudes and prefix their common sign.
- To add two decimals with unlike signs, subtract the smaller magnitude from the larger, then prefix the sign of the decimal number having the larger magnitude.
Example \(\PageIndex{3}\)
Simplify:
- \(-2.3+(-0.015)\)
- \(-8.4+6 .95\)
Solution
- In this problem, note that we have like signs. Hence, we add the magnitudes and prefix the common sign. \[-2.3+(-0.015)=-2.315 \nonumber \] \[\begin{array}{r}{2.300} \\ {+0.015} \\ \hline 2.315\end{array} \nonumber \]
- In this problem, note that we have unlike signs. Thus, we first subtract the smaller magnitude from the larger magnitude, then prefix the sign of the decimal number with the larger magnitude. \[-8.4+6.95=-1.45 \nonumber\] \[\begin{array}{r}{8.40} \\ {-6.95} \\ \hline 1.45\end{array} \nonumber \]
Hence, \(-2.3+(-0.015) =-2.315\) and \(-8.4+6 .95 = -1.45\)
Exercise \(\PageIndex{3}\)
Simplify: \(-22.6+18.47\).
- Answer
-
\(-4.13\)
Subtraction still means “add the opposite.”
Example \(\PageIndex{4}\)
Simplify:
- \(-5.6-8.4\)
- \(-7.9-(-5.32)\)
Solution
- In this problem, first we add the oppposite. Then we note that we have like signs. Hence, we add the magnitudes and prefix the common sign. \[\begin{aligned}-5.6-8.4 &=-5.6+(-8.4) \\ &=-14.0 \end{aligned} \nonumber\] \[\begin{array}{r}{5.6} \\ {+8.4} \\ \hline 14.0\end{array} \nonumber \]
- In this problem, first we add the opposite. Then we note that we have unlike signs. Thus, we first subtract the smaller magnitude from the larger magnitude, then prefix the sign of the decimal number with the larger magnitude.\[\begin{aligned}-7.9-(-5.32) &=-7.9+5.32 \\ &=-2.58 \end{aligned} \nonumber\] \[\begin{array}{r}{7.90} \\ {-5.32} \\ \hline 2.58\end{array} \nonumber \]
Hence, \(-5.6-8.4=-14.0\) and \(-7.9-(-5.32) = -2.58\).
Exercise \(\PageIndex{4}\)
Simplify: \(-22.6-18.47\).
- Answer
-
\(-41.07\)
Multiplication and Division of Decimals
The sign rules for decimal multiplication and division are the same as the sign rules used for integers and fractions.
Sign Rules for multiplication and division
When multiplying or dividing two decimal numbers, use the following rules:
- Like signs give a positive result
- Unlike signs give a negative result
Multiplication of decimal numbers is fairly straightforward. First multiply the magnitudes of the numbers, ignoring the decimal points, then count the number of digits to the right of the decimal point in each factor. Place the decimal point in the product so that the number of digits to the right of the decimal points equals the sum of number of digits to the right of the decimal point in each factor.
Example \(\PageIndex{5}\)
Simplify: \((-1.96)(2.8)\).
Solution
Multiply the magnitudes. The first decimal number has two digits to the right of the decimal point, the second has one digit to the right of the decimal point. Thus, we must place a total of three digits to the right of the decimal point in the product.
\[(-1.96)(2.8)=-5.488 \nonumber \]
\[\begin{array}{r}{1.96} \\ { \times 2.8} \\ \hline 1568 \\ {392\;\;} \\ \hline 5.488\end{array} \nonumber \]
Note that unlike signs yield a negative product.
Exercise \(\PageIndex{5}\)
Simplify: \((-12.5)(-23.4)\).
- Answer
-
\(292.50\)
When dividing signed decimal numbers, ignore the signs and divide the magnitudes. Push the decimal point in the divisor to the end of the divisor, then move the decimal point in the dividend an equal number of spaces. This sets the decimal point in the quotient.
Example \(\PageIndex{6}\)
Simplify: \(-4.392 \div(-0.36)\).
Solution
Divide the magnitudes. Move the decimal in the divisor to the end of the divisor. Move the decimal in the dividend an equal number of places (two places) to the right.
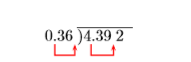
Place the decimal point in the quotient directly above the new position of the decimal point in the dividend, then divide.
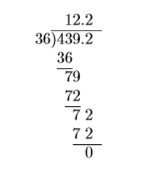
Like signs yield a positive result. Hence, \(-4.392 \div(-0.36)=12.2\).
Exercise \(\PageIndex{6}\)
Simplify: \(-5.76 / 3.2\).
- Answer
-
\(-1.8\)
Order of Operations
Decimal numbers obey the same Rules Guiding Order of Operations as do the integers and fractions.
Rules Guiding Order of Operations
When evaluating expressions, proceed in the following order.
- Evaluate expressions contained in grouping symbols first. If grouping symbols are nested, evaluate the expression in the innermost pair of grouping symbols first.
- Evaluate all exponents that appear in the expression.
- Perform all multiplications and divisions in the order that they appear in the expression, moving left to right.
- Perform all additions and subtractions in the order that they appear in the expression, moving left to right.
Example \(\PageIndex{7}\)
Given \(x=-0.12\), evaluate \(-x^{2}\).
Solution
Following Tips for Evaluating Algebraic Expressions, first replace all occurrences of variable \(x\) in the expression \(-x^2\) with open parentheses. Next, substitute \(-0.12\) for \(x\) in the open parentheses, then simplify.
\[\begin{aligned} -x^{2} &=-(\quad)^{2} \quad \color{Red} \text { Replace } x \text { with open parentheses. } \\ &=-(-0.12)^{2} \quad \color{Red} \text { Substitute }-0.12 \text { for } x . \\ &=-(0.0144) \quad \color{Red} \text { Exponent: }(-0.12)^{2}=0.0144 \\ &=-0.0144 \quad \color{Red} \text { Negate. } \end{aligned} \nonumber \]
Note that we square first, then we negate second. Thus, if \(x = -0.12\), then \(-x^{2}=-0.0144\).
Exercise \(\PageIndex{7}\)
Given \(y=-0.2\), evaluate: \(-y^{4}\).
- Answer
-
\(-0.0016\)
Example \(\PageIndex{8}\)
Given \(x=-0.3\), evaluate \(1.2 x^{2}-3.4 x\).
Solution
Following Tips for Evaluating Algebraic Expressions, first replace all occurrences of variable \(x\) in the expression \(1.2 x^{2}-3.4 x\) with open parentheses. Next, substitute \(-0.3\) for \(x\) in the open parentheses, then simplify.
\[\begin{aligned} 1.2 x^{2}-3.4 x &=1.2(\quad)^{2}-3.4(\quad) \quad \color{Red} \text { Replace } x \text { with parentheses. } \\ &=1.2(-0.3)^{2}-3.4(-0.3) \quad \color{Red} \text { Substitute }-0.3 \text { for } x . \\ &=1.2(0.09)-3.4(-0.3) \quad \color{Red} \text { Exponent: }(-0.3)^{2}=0.09 \\ &=0.108-(-1.02) \quad \color{Red} \text { Multiply: } 1.2(0.09)=0.108 \text { and } \\ &=0.108+1.02 \quad \color{Red} \text { Add the opposite. } \\ &=1.128 \quad \color{Red} \text { Simplify. } \end{aligned} \nonumber \]
Thus, if \(x = -0.3\), then \(1.2 x^{2}-3.4 x=1.128\).
Exercise \(\PageIndex{8}\)
Given \(y=-0.15\), \(\text { evaluate: } -1.4 y^{2}+2.2 y \).
- Answer
-
\(-0.3615\)
We saw earlier that we can change a fraction to a decimal by dividing.
Example \(\PageIndex{9}\)
Given \(x=2 / 5\), evaluate \(-3.2 x+5\).
Solution
Following Tips for Evaluating Algebraic Expressions, first replace all occurrences of variable \(x\) in the expression \(-3.2x+5\) with open parentheses. Next, substitute \(2/5\) for \(x\) in the open parentheses.
\[\begin{aligned} -3.2 x+5 &=-3.2(\; )+5 \quad \color{Red} \text { Replace } x \text { with open parentheses. } \\ &=-3.2\left(\dfrac{2}{5}\right)+5 \quad \color{Red} \text { Substitute } 2 / 5 \text { for } x \end{aligned} \nonumber \]
One approach is to change \(2/5\) to a decimal by dividing the numerator by the denominator. Thus, \(2/5=0 .4\).
\[\begin{aligned} &=-3.2(0.4)+5 \quad \color{Red} {\text { Replace } 2 / 5 \text { with } 0.4} \\ &=-1.28+5 \quad \color{Red} \text { Multiply: }-3.2(0.4)=-1.28 \\ &=3.72 \quad \color{Red} \text { Add: }-1.28+5=3.72 \end{aligned} \nonumber \]
Thus, if \(x =2 /5\), then \(-3.2x+5=3 .72\).
Exercise \(\PageIndex{9}\)
Given \(y=-3 / 4\), evaluate \(-2.3 y+7\).
- Answer
-
\(8.725\)
As we saw in Example \(\PageIndex{2}\), we can easily change a terminating decimal into a fraction by placing the number (without the decimal point) over the proper power of ten. The choice of the power of ten should match the number of digits to the right of the decimal point. For example:
\[0.411=\dfrac{411}{1000} \quad \text { and } \quad 3.11=\dfrac{311}{100} \quad \text { and } \quad 15.1111=\dfrac{151111}{10000} \nonumber \]
Note that the number of zeros in each denominator matches the number of digits to the right of the decimal point.
Example \(\PageIndex{10}\)
Given \(y =-0.25\), evaluate \(-\dfrac{3}{5} y+4\).
Solution
Following Tips for Evaluating Algebraic Expressions, first replace all occurrences of variable \(y\) in the expression \(-(3/5)y+4\) with open parentheses. Next, substitute \(-0.25\) for \(y\) in the open parentheses.
\[\begin{aligned} -\dfrac{3}{5} y+4 &=-\dfrac{3}{5}(\quad)+4 \quad \color{Red} \text { Replace } y \text { with open parentheses. } \\ &=-\dfrac{3}{5}(-0.25)+4 \quad \color{Red} \text { Substitute }-0.25 \text { for } y \end{aligned} \nonumber \]
Place \(25\) over \(100\) to determine that \(-0.25 = -25/100\), or after reduction, \(-0.25 =-1/4\).
\[\begin{aligned}
&=-\dfrac{3}{5}\left(-\dfrac{1}{4}\right)+4 \quad \color{Red} \text { Replace }-0.25 \text { with } -1/4 \\
&=\dfrac{3}{20}+4 \quad \color{Red} \text { Multiply: } -\dfrac{3}{5}\left(-\dfrac{1}{4}\right)=\dfrac{3}{20} \\
&=\dfrac{3}{20}+\dfrac{80}{20} \quad \color{Red} \text { Make equivalent fractions with LCD. } \\
&=\dfrac{83}{20} \quad \color{Red} \text { Add. }
\end{aligned} \nonumber \]
Thus, if \(y =-0.25\), then \(-(3 / 5) y+4=83 / 20\).
Exercise \(\PageIndex{10}\)
Given \(z=-0.4\), evaluate: \(5-\dfrac{4}{5} z\).
- Answer
-
\(133/25\)
Rounding Using the Graphing Calculator
Here is the algorithm for rounding a decimal number to a particular place.
Rules for rounding
To round a number to a particular place, follow these steps:
- Mark the place you wish to round to. The digit in this place is called the rounding digit.
- Mark the digit in the place to the immediate right of the rounding digit. This is called the test digit.
- If the test digit is greater than or equal to \(5\), add \(1\) to the rounding digit, then replace all digits to the right of the rounding digit with zeros. Trailing zeros to the right of the decimal point may be deleted.
- If the test digit is less than \(5\), keep the rounding digit the same, then replace all digits to the right of the rounding digit with zeros. Trailing zeros to the right of the decimal point may be deleted.
Example \(\PageIndex{11}\)
Use your graphing calculator to evaluate \(125 x^{3}-17.5 x+44.8\) at \(x = -3.13\). Round your answer to the nearest tenth.
Solution
First, store \(-3.13\) in the variable \(X\) with the following keystrokes.

The result is shown in the first image in Figure \(\PageIndex{1}\). Next, enter the expression \(125 x^{3}-17.5 x+44.8\) with the following keystrokes.

The result is shown in the second image in Figure \(\PageIndex{1}\). Thus, the answer is approximately \(-3733.462125\). We now need to round this answer to the nearest tenth. Mark the rounding digit in the tenths place and the test digit to its immediate right.
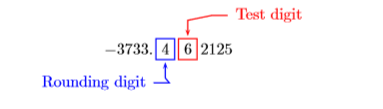
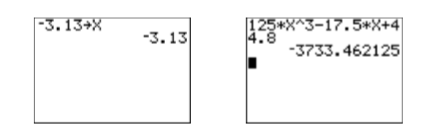
Figure \(\PageIndex{1}\): Evaluate \(125 x^{3}-17.5 x+44.8\) at \(x=-3.13\)
Because the test digit is greater than or equal to \(5\), add \(1\) to the rounding digit, then replace all digits to the right of the rounding digit with zeros.
\[-3733.462125 \approx-3733.500000 \nonumber \]
Delete the trailing zeros from end of the fractional part of a decimal. This does not change our answer’s value.
\[-3733.462125 \approx-3733.5 \nonumber \]
Therefore, if \(x =-3.13\). then to the nearest tenth:
\[125 x^{3}-17.5 x+44.8 \approx-3733.5 \nonumber \]
Exercise \(\PageIndex{11}\)
Evaluate \(x^{3}-3 x\) at \(x =-1.012\). Round to the nearest hundredth.
- Answer
-
\(2.0\)
Contributors
David Arnold (Retired Professor (Mathematics) at College of the Redwoods)


