5.4: Multiply Polynomials
( \newcommand{\kernel}{\mathrm{null}\,}\)
By the end of this section, you will be able to:
- Multiply monomials
- Multiply a polynomial by a monomial
- Multiply a binomial by a binomial
- Multiply a polynomial by a polynomial
- Multiply special products
- Multiply polynomial functions
Before you get started, take this readiness quiz.
Multiply Monomials
We are ready to perform operations on polynomials. Since monomials are algebraic expressions, we can use the properties of exponents to multiply monomials.
Multiply:
- (3x2)(−4x3)
- (56x3y)(12xy2).
- Answer a
-
(3x2)(−4x3)Use the Commutative Property to rearrange the terms.3·(−4)·x2·x3−12x5
- Answer b
-
(56x3y)(12xy2)Use the Commutative Property to rearrange the terms.56·12·x3·x·y·y2Multiply.10x4y3
Multiply:
- (5y7)(−7y4)
- (25a4b3)(15ab3)
- Answer a
-
−35y11
- Answer b
-
375a5b6
Multiply:
- (−6b4)(−9b5)
- (23r5s)(12r6s7).
- Answer a
-
54b9
- Answer b
-
276r11s8
Multiply a Polynomial by a Monomial
Multiplying a polynomial by a monomial is really just applying the Distributive Property.
Multiply:
- −2y(4y2+3y−5)
- 3x3y(x2−8xy+y2).
- Answer a
-
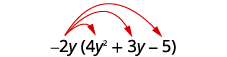
Distribute. 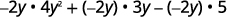
Multiply. 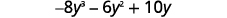
- Answer b
-
3x3y(x2−8xy+y2)Distribute.3x3y⋅x2+(3x3y)⋅(−8xy)+(3x3y)⋅y2Multiply.3x5y−24x4y2+3x3y3
Multiply:
- −3y(5y2+8y7)
- 4x2y2(3x2−5xy+3y2)
- Answer a
-
−15y3−24y8
- Answer b
-
12x4y2−20x3y3+12x2y4
Multiply:
- 4x2(2x2−3x+5)
- −6a3b(3a2−2ab+6b2)
- Answer a
-
8x4−12x3+20x2
- Answer b
-
−18a5b+12a4b2−36a3b3
Multiply a Binomial by a Binomial
Just like there are different ways to represent multiplication of numbers, there are several methods that can be used to multiply a binomial times a binomial. We will start by using the Distributive Property.
Multiply:
- (y+5)(y+8)
- (4y+3)(2y−5).
- Answer
-
ⓐ
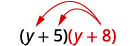
Distribute (y+8). 
Distribute again. 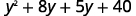
Combine like terms. 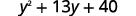
ⓑ
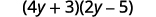
Distribute. 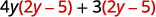
Distribute again. 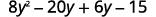
Combine like terms. 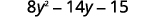
Multiply:
- (x+8)(x+9)
- (3c+4)(5c−2).
- Answer a
-
x2+17x+72
- Answer b
-
15c2+14c−8
Multiply:
- (5x+9)(4x+3)
- (5y+2)(6y−3).
- Answer a
-
20x2+51x+27
- Answer b
-
30y2−3y−6
If you multiply binomials often enough you may notice a pattern. Notice that the first term in the result is the product of the first terms in each binomial. The second and third terms are the product of multiplying the two outer terms and then the two inner terms. And the last term results from multiplying the two last terms,
We abbreviate “First, Outer, Inner, Last” as FOIL. The letters stand for ‘First, Outer, Inner, Last’. We use this as another method of multiplying binomials. The word FOIL is easy to remember and ensures we find all four products.
Let’s multiply (x+3)(x+7) using both methods.

We summarize the steps of the FOIL method below. The FOIL method only applies to multiplying binomials, not other polynomials!

When you multiply by the FOIL method, drawing the lines will help your brain focus on the pattern and make it easier to apply.
Now we will do an example where we use the FOIL pattern to multiply two binomials.
Multiply:
- (y−7)(y+4)
- (4x+3)(2x−5).
- Answer
-
a.

b.

Multiply:
- (x−7)(x+5)
- (3x+7)(5x−2).
- Answer
-
a. x2−2x−35
b. 15x2+29x−14
Multiply:
- (b−3)(b+6)
- (4y+5)(4y−10).
- Answer
-
a. b2+3b−18
b. 16y2−20y−50
The final products in the last example were trinomials because we could combine the two middle terms. This is not always the case.
Multiply:
- (n2+4)(n−1)
- (3pq+5)(6pq−11).
- Answer
-
a.
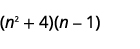
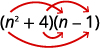
Step 1. Multiply the First terms. 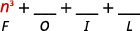
Step 2. Multiply the Outer terms. 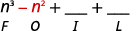
Step 3. Multiply the Inner terms. 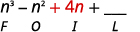
Step 4. Multiply the Last terms. 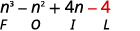
Step 5. Combine like terms—there are none. 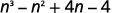
b.
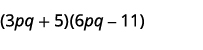
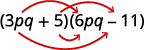
Step 1. Multiply the First terms. 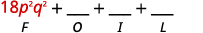
Step 2. Multiply the Outer terms. 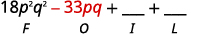
Step 3. Multiply the Inner terms. 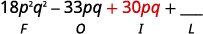
Step 4. Multiply the Last terms. 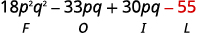
Step 5. Combine like terms. 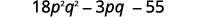
Multiply:
- (x2+6)(x−8)
- (2ab+5)(4ab−4).
- Answer
-
a. x3−8x2+6x−48
b. 8a2b2+12ab−20
Multiply:
- (y2+7)(y−9)
- (2xy+3)(4xy−5).
- Answer
-
a. y3−9y2+7y−63
b. 8x2y2+2xy−15
The FOIL method is usually the quickest method for multiplying two binomials, but it only works for binomials. You can use the Distributive Property to find the product of any two polynomials. Another method that works for all polynomials is the Vertical Method. It is very much like the method you use to multiply whole numbers. Look carefully at this example of multiplying two-digit numbers.

Now we’ll apply this same method to multiply two binomials.
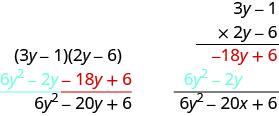
Multiply using the Vertical Method: (3y−1)(2y−6).
- Answer
-
It does not matter which binomial goes on the top.
3y−1×2y−6_Multiply 3y−1 by −6.−18y+6partial productMultiply 3y−1 by 2y.6y2−2y_partial productAdd like terms.6y2−20y+6
Notice the partial products are the same as the terms in the FOIL method.
Multiply using the Vertical Method: (5m−7)(3m−6).
- Answer
-
15m2−51m+42
Multiply using the Vertical Method: (6b−5)(7b−3).
- Answer
-
42b2−53b+15
We have now used three methods for multiplying binomials. Be sure to practice each method, and try to decide which one you prefer. The methods are listed here all together, to help you remember them.
To multiply binomials, use the:
- Distributive Property
- FOIL Method
- Vertical Method
Multiply a Polynomial by a Polynomial
We have multiplied monomials by monomials, monomials by polynomials, and binomials by binomials. Now we’re ready to multiply a polynomial by a polynomial. Remember, FOIL will not work in this case, but we can use either the Distributive Property or the Vertical Method.
Multiply (b+3)(2b2−5b+8) using ⓐ the Distributive Property and ⓑ the Vertical Method.
- Answer
-
a.
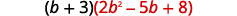
Distribute. 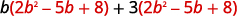
Multiply. 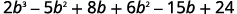
Combine like terms. 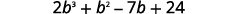
b. It is easier to put the polynomial with fewer terms on the bottom because we get fewer partial products this way.
Multiply (2b2−5b+8) by 3.
Multiply (2b2−5b+8) by b.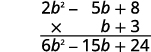
Add like terms. 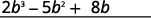

Multiply (y−3)(y2−5y+2) using ⓐ the Distributive Property and ⓑ the Vertical Method.
- Answer
-
a. y3−8y2+17y−6
b. y3−8y2+17y−6
Multiply (x+4)(2x2−3x+5) using a) the Distributive Property and b) The Vertical Method.
- Answer
-
a. and b. 2x3+5x2−7x+20
We have now seen two methods you can use to multiply a polynomial by a polynomial. After you practice each method, you’ll probably find you prefer one way over the other. We list both methods are listed here, for easy reference.
To multiply a trinomial by a binomial, use the:
- Distributive Property
- Vertical Method
Multiply Special Products
Mathematicians like to look for patterns that will make their work easier. A good example of this is squaring binomials. While you can always get the product by writing the binomial twice and multiplying them, there is less work to do if you learn to use a pattern. Let’s start by looking at three examples and look for a pattern.
Look at these results. Do you see any patterns?
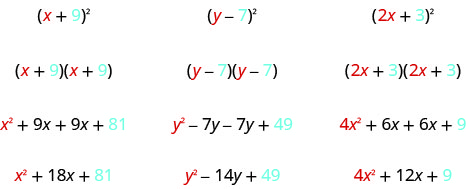
What about the number of terms? In each example we squared a binomial and the result was a trinomial.
(a+b)2=___+___+___
Now look at the first term in each result. Where did it come from?
The first term is the product of the first terms of each binomial. Since the binomials are identical, it is just the square of the first term!
(a+b)2=a2+___+___
To get the first term of the product, square the first term.
Where did the last term come from? Look at the examples and find the pattern.
The last term is the product of the last terms, which is the square of the last term.
(a+b)2=___+___+b2
To get the last term of the product, square the last term.
Finally, look at the middle term. Notice it came from adding the “outer” and the “inner” terms—which are both the same! So the middle term is double the product of the two terms of the binomial.
(a+b)2=___+2ab+___
(a−b)2=___−2ab+___
To get the middle term of the product, multiply the terms and double their product.
Putting it all together:
If a and b are real numbers,

To square a binomial, square the first term, square the last term, double their product.
Multiply: a. (x+5)2 b. (2x−3y)2.
- Answer
-
a.
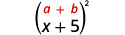
Square the first term. 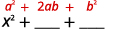
Square the last term. 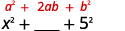
Double their product. 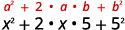
Simplify. 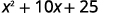
b.
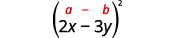
Use the pattern. 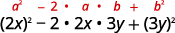
Simplify. 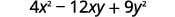
Multiply: a.(x+9)2 b. (2c−d)2.
- Answer
-
a. x2+18x+81
b. 4c2−4cd+d2
Multiply: a. (y+11)2 b. (4x−5y)2.
- Answer
-
a. y2+22y+121
b. 16x2−40xy+25y2
We just saw a pattern for squaring binomials that we can use to make multiplying some binomials easier. Similarly, there is a pattern for another product of binomials. But before we get to it, we need to introduce some vocabulary.
A pair of binomials that each have the same first term and the same last term, but one is a sum and one is a difference is called a conjugate pair and is of the form (a−b), (a+b).
A conjugate pair is two binomials of the form
(a−b),(a+b).
The pair of binomials each have the same first term and the same last term, but one binomial is a sum and the other is a difference.
There is a nice pattern for finding the product of conjugates. You could, of course, simply FOIL to get the product, but using the pattern makes your work easier. Let’s look for the pattern by using FOIL to multiply some conjugate pairs.
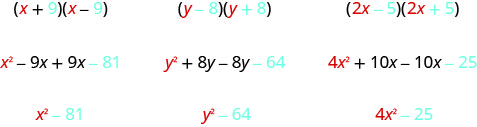
What do you observe about the products?
The product of the two binomials is also a binomial! Most of the products resulting from FOIL have been trinomials.
Each first term is the product of the first terms of the binomials, and since they are identical it is the square of the first term.
(a+b)(a−b)=a2−___
To get the first term, square the first term.
The last term came from multiplying the last terms, the square of the last term.
(a+b)(a−b)=a2−b2
To get the last term, square the last term.
Why is there no middle term? Notice the two middle terms you get from FOIL combine to 0 in every case, the result of one addition and one subtraction.
The product of conjugates is always of the form a2−b2. This is called a difference of squares.
This leads to the pattern:
If a and b are real numbers,

The product is called a difference of squares.
To multiply conjugates, square the first term, square the last term, write it as a difference of squares.
Multiply using the product of conjugates pattern: a. (2x+5)(2x−5) b. (5m−9n)(5m+9n).
- Answer
-
a.
Are the binomials conjugates? 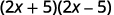
It is the product of conjugates. 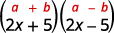
Square the first term, 2x.2x. 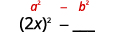
Square the last term, 5.5. 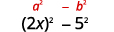
Simplify. The product is a difference of squares. 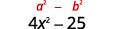
b.
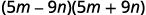
This fits the pattern. 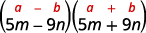
Use the pattern. 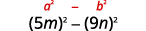
Simplify. 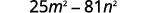
Multiply: a. (6x+5)(6x−5) b. (4p−7q)(4p+7q).
- Answer
-
a. 36x2−25
b. 16p2−49q2
Multiply: a. (2x+7)(2x−7) b.(3x−y)(3x+y).
- Answer
-
a. 4x2−49 b. 9x2−y2
We just developed special product patterns for Binomial Squares and for the Product of Conjugates. The products look similar, so it is important to recognize when it is appropriate to use each of these patterns and to notice how they differ. Look at the two patterns together and note their similarities and differences.
| Binomial Squares | Product of Conjugates |
|---|---|
| (a+b)2=a2+2ab+b2 | (a−b)(a+b)=a2−b2 |
| (a−b)2=a2−2ab+b2 | |
| • Squaring a binomial | • Multiplying conjugates |
| • Product is a trinomial | • Product is a binomial. |
| • Inner and outer terms with FOIL are the same. | • Inner and outer terms with FOIL are opposites. |
| • Middle term is double the product of the terms | • There is no middle term. |
Choose the appropriate pattern and use it to find the product:
a. (2x−3)(2x+3) b. (8x−5)2 c. (6m+7)2 d. (5x−6)(6x+5).
- Answer
-
a. (2x−3)(2x+3)
These are conjugates. They have the same first numbers, and the same last numbers, and one binomial is a sum and the other is a difference. It fits the Product of Conjugates pattern.
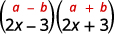
Use the pattern. 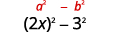
Simplify. 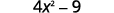
b. (8x−5)2
We are asked to square a binomial. It fits the binomial squares pattern.
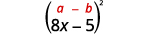
Use the pattern. 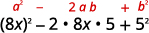
Simplify. 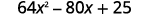
c. (6m+7)2
Again, we will square a binomial so we use the binomial squares pattern.
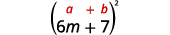
Use the pattern. 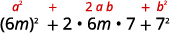
Simplify. 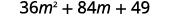
d. (5x−6)(6x+5)
This product does not fit the patterns, so we will use FOIL.
(5x−6)(6x+5)Use FOIL.30x2+25x−36x−30Simplify.30x2−11x−30
Choose the appropriate pattern and use it to find the product:
a. (9b−2)(2b+9) b. (9p−4)2 c. (7y+1)2 d. (4r−3)(4r+3).
- Answer
-
a. FOIL; 18b2+77b−18
b. Binomial Squares; 81p2−72p+16
c. Binomial Squares; 49y2+14y+1
d. Product of Conjugates; 16r2−9
Choose the appropriate pattern and use it to find the product:
a. (6x+7)2 b. (3x−4)(3x+4) c. (2x−5)(5x−2) d. (6n−1)2.
- Answer
-
a. Binomial Squares; 36x2+84x+49 b. Product of Conjugates; 9x2−16 c. FOIL; 10x2−29x+10 d. Binomial Squares; 36n2−12n+1
Multiply Polynomial Functions
Just as polynomials can be multiplied, polynomial functions can also be multiplied.
For functions f(x) and g(x),
(f·g)(x)=f(x)·g(x)
For functions f(x)=x+2 and g(x)=x2−3x−4, find:
- (f·g)(x)
- (f·g)(2).
- Answer
-
a.
(f·g)(x)=f(x)·g(x)Substitute for f(x) and g(x)(f·g)(x)=(x+2)(x2−3x−4)Multiply the polynomials.(f·g)(x)=x(x2−3x−4)+2(x2−3x−4)Distribute.(f·g)(x)=x3−3x2−4x+2x2−6x−8Combine like terms.(f·g)(x)=x3−x2−10x−8
b. In part a. we found (f·g)(x) and now are asked to find (f·g)(2).
(f·g)(x)=x3−x2−10x−8To find (f·g)(2), substitute x=2.(f·g)(2)=23−22−10·2−8(f·g)(2)=8−4−20−8(f·g)(2)=−24
For functions f(x)=x−5 and g(x)=x2−2x+3, find
- (f·g)(x)
- (f·g)(2).
- Answer a
-
(f·g)(x)=x3−7x2+13x−15
- Answer b
-
(f·g)(2)=−9
For functions f(x)=x−7 and g(x)=x2+8x+4, find
- (f·g)(x)
- (f·g)(2).
- Answer a
-
(f·g)(x)=x3+x2−52x−28
- Answer a
-
(f·g)(2)=−120
Access this online resource for additional instruction and practice with multiplying polynomials.
- Introduction to special products of binomials
Key Concepts
- How to use the FOIL method to multiply two binomials.
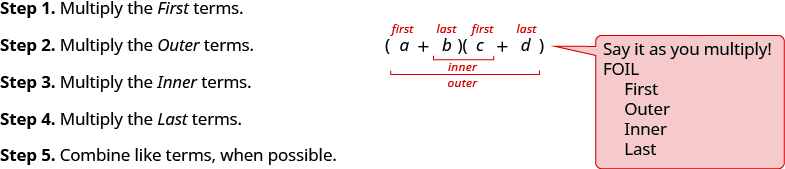
- Multiplying Two Binomials: To multiply binomials, use the:
- Distributive Property
- FOIL Method
- Multiplying a Polynomial by a Polynomial: To multiply a trinomial by a binomial, use the:
- Distributive Property
- Vertical Method
- Binomial Squares Pattern
If a and b are real numbers,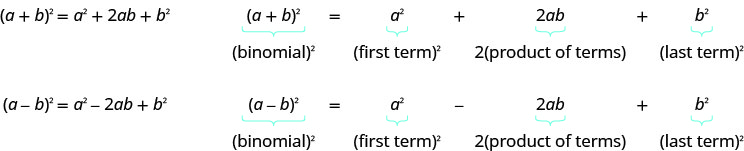
- Product of Conjugates Pattern
If a, b are real numbers
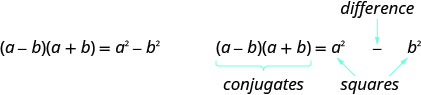
The product is called a difference of squares.
To multiply conjugates, square the first term, square the last term, write it as a difference of squares. - Comparing the Special Product Patterns
Binomial Squares Product of Conjugates (a+b)2=a2+2ab+b2 (a−b)2=a2−2ab+b2 (a−b)(a+b)=a2−b2 • Squaring a binomial • Multiplying conjugates • Product is a trinomial • Product is a binomial. • Inner and outer terms with FOIL are the same. • Inner and outer terms with FOIL are opposites. • Middle term is double the product of the terms • There is no middle term. - Multiplication of Polynomial Functions:
- For functions f(x) and g(x),
(f⋅g)(x)=f(x)⋅g(x)
- For functions f(x) and g(x),
Glossary
- conjugate pair
- A conjugate pair is two binomials of the form (a−b) and (a+b). The pair of binomials each have the same first term and the same last term, but one binomial is a sum and the other is a difference.


