3.6: Parallel and Perpendicular Lines

Last updated
Save as PDF

Page ID: 18345

Anonymous
LibreTexts

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Learning Objectives

Determine the slopes of parallel and perpendicular lines.
Find equations of parallel and perpendicular lines

Definition of Parallel and Perpendicular

Parallel lines are lines in the same plane that never intersect. Two nonvertical lines in the same plane, with slopes $m_{1}$ and $m_{2}$, are parallel if their slopes are the same, $m_{1}=m_{2}$. Consider the following two lines:

Consider their corresponding graphs:

$Screenshot (628).png$

Figure $\PageIndex{1}$

Both lines have a slope $m=\frac{3}{4}$ and thus are parallel.

Perpendicular lines are lines in the same plane that intersect at right angles ($90$ degrees). Two nonvertical lines in the same plane, with slopes $m_{1}$ and $m_{2}$, are perpendicular if the product of their slopes is $−1: m1⋅m2=−1$. We can solve for $m_{1}$ and obtain $m_{1}=\frac{−1}{m_{2}}$. In this form, we see that perpendicular lines have slopes that are negative reciprocals, or opposite reciprocals. For example, if given a slope

$m=-\frac{5}{8}$

then the slope of a perpendicular line is the opposite reciprocal:

$m_{\perp}=\frac{8}{5}$

The mathematical notation $m_{⊥}$ reads “$m$ perpendicular.” We can verify that two slopes produce perpendicular lines if their product is $−1$.

$m\cdot m_{\perp}=-\frac{5}{8}\cdot\frac{8}{5}=-\frac{40}{40}=-1\quad\color{Cerulean}{\checkmark}$

Geometrically, we note that if a line has a positive slope, then any perpendicular line will have a negative slope. Furthermore, the rise and run between two perpendicular lines are interchanged.

$Screenshot (629).png$

Figure $\PageIndex{2}$

Perpendicular lines have slopes that are opposite reciprocals, so remember to find the reciprocal and change the sign. In other words,

If $m=\frac{a}{b}$, then $m_{\perp}=-\frac{b}{a}$

Determining the slope of a perpendicular line can be performed mentally. Some examples follow

Table $\PageIndex{1}$
Given slope	Slope of perpendicular line
$m=\frac{1}{2}$	$m_{\perp}=-2$
$m=-\frac{3}{4}$	$m_{\perp}=\frac{4}{3}$
$m=3$	$m_{\perp}=-\frac{1}{3}$
$m=-4$	$m_{\perp}=\frac{1}{4}$

Example $\PageIndex{1}$

Determine the slope of a line parallel to $y=−5x+3$.

Solution:

Since the given line is in slope-intercept form, we can see that its slope is $m=−5$. Thus the slope of any line parallel to the given line must be the same, $m_{∥}=−5$. The mathematical notation $m_{∥}$ reads “$m$ parallel.”

Answer:

$m_{∥}=−5$

Example $\PageIndex{2}$

Determine the slope of a line perpendicular to $3x−7y=21$.

Solution:

First, solve for $y$ and express the line in slope-intercept form.

In this form, we can see that the slope of the given line is $m=\frac{3}{7}$, and thus $m_{⊥}=−\frac{7}{3}$.

Answer:

$m_{⊥}=−\frac{7}{3}$

Exercise $\PageIndex{1}$

Find the slope of the line perpendicular to $15x+5y=20$.

Answer: $m_{\perp}=\frac{1}{3}$

Finding Equations of Parallel and Perpendicular Lines

We have seen that the graph of a line is completely determined by two points or one point and its slope. Often you will be asked to find the equation of a line given some geometric relationship—for instance, whether the line is parallel or perpendicular to another line.

Example $\PageIndex{3}$

Find the equation of the line passing through $(6, −1)$ and parallel to $y=\frac{1}{2}x+2$

Solution

Here the given line has slope $m=\frac{1}{2}$, and the slope of a line parallel is $m_{∥}=\frac{1}{2}$. Since you are given a point and the slope, use the point-slope form of a line to determine the equation.

$\begin{array}{cc}{\color{Cerulean}{Point}}&{\color{Cerulean}{Slope}}\\{(6,-1)}&{m_{\parallel}=\frac{1}{2}} \end{array}$

Answer:

$y=\frac{1}{2}x-4$

It is important to have a geometric understanding of this question. We were asked to find the equation of a line parallel to another line passing through a certain point.

$Screenshot (630).png$

Figure $\PageIndex{3}$

Through the point $(6, −1)$ we found a parallel line, $y=\frac{1}{2}x−4$, shown dashed. Notice that the slope is the same as the given line, but the $y$-intercept is different. If we keep in mind the geometric interpretation, then it will be easier to remember the process needed to solve the problem.

Example $\PageIndex{4}$

Find the equation of the line passing through $(−1, −5)$ and perpendicular to $y=−\frac{1}{4}x+2$.

Solution:

The given line has slope $m=−\frac{1}{4}$, and thus $m_{⊥}=+\frac{4}{1}=4$. Substitute this slope and the given point into point-slope form.

$\begin{array}{cc} {\color{Cerulean}{Point}}&{\color{Cerulean}{Slope}}\\{(-1,-5)}&{m_{\perp}=4}\end{array}$

Answer:

$y=4x-1$

Geometrically, we see that the line $y=4x−1$, shown dashed below, passes through $(−1, −5)$ and is perpendicular to the given line.

$Screenshot (631).png$

Figure $\PageIndex{4}$

It is not always the case that the given line is in slope-intercept form. Often you have to perform additional steps to determine the slope. The general steps for finding the equation of a line are outlined in the following example.

Example $\PageIndex{5}$

Find the equation of the line passing through $(8, −2)$ and perpendicular to $6x+3y=1$.

Solution:

Step 1: Find the slope $m$. First, find the slope of the given line. To do this, solve for $y$ to change standard form to slope-intercept form, $y=mx+b$.

$\begin{aligned} 6x+3y&=1 \\ 6x+3y\color{Cerulean}{-6x}&=1\color{Cerulean}{-6x} \\ 3y&=-6x+1 \\ \frac{3y}{\color{Cerulean}{3}}&=\frac{-6x+1}{\color{Cerulean}{3}} \\ y&=\frac{-6x}{3}+\frac{1}{3}\\y&=-2x+\frac{1}{3} \end{aligned}$

In this form, you can see that the slope is $m=−2=−\frac{2}{1}$, and thus $m_{⊥}=\frac{−1}{−2}=+\frac{1}{2}$.

Step 2: Substitute the slope you found and the given point into the point-slope form of an equation for a line. In this case, the slope is $m_{⊥}=\frac{1}{2}$ and the given point is $(8, −2)$.

$\begin{aligned} y-y_{1}&=m(x-x_{1}) \\ y-(-2)&=\frac{1}{2}(x-8) \end{aligned}$

Step 3: Solve for $y$.

Answer:

$y=\frac{1}{2}x−6$

Example $\PageIndex{6}$

Find the equation of the line passing through $(\frac{7}{2}, 1)$ and parallel to $2x+14y=7$.

Solution:

Find the slope $m$ by solving for $y$.

$\begin{aligned} 2x+14y&=7 \\ 2x+14y\color{Cerulean}{-2x}&=7\color{Cerulean}{-2x} \\ 14y&=-2x+7 \\ \frac{14y}{\color{Cerulean}{14}}&=\frac{-2x+7}{\color{Cerulean}{14}} \\ y&=\frac{-2x}{14}+\frac{7}{14} \\ y&=-\frac{1}{7}x+\frac{1}{2} \end{aligned}$

The given line has the slope $m=−\frac{1}{7}$, and so $m_{∥}=−\frac{1}{7}$. We use this and the point $(\frac{7}{2}, 1)$ in point-slope form.

$\begin{aligned} y-y_{1}&=m(x-x_{1}) \\ y-1&=-\frac{1}{7}\left(x-\frac{7}{2} \right) \\ y-1&=-\frac{1}{7}x+\frac{1}{2} \\ y-1\color{Cerulean}{+1}&=-\frac{1}{7}x+\frac{1}{2}\color{Cerulean}{+1} \\ y&=-\frac{1}{7}x+\frac{1}{2}+\color{Cerulean}{\frac{2}{2}} \\ y&=-\frac{1}{7}x+\frac{3}{2} \end{aligned}$

Answer:

$y=-\frac{1}{7}x+\frac{3}{2}$

Exercise $\PageIndex{2}$

Find the equation of the line perpendicular to $x−3y=9$ and passing through $(−\frac{1}{2}, 2)$.

Answer: $y=-3x+\frac{1}{2}$

When finding an equation of a line perpendicular to a horizontal or vertical line, it is best to consider the geometric interpretation.

Example $\PageIndex{7}$

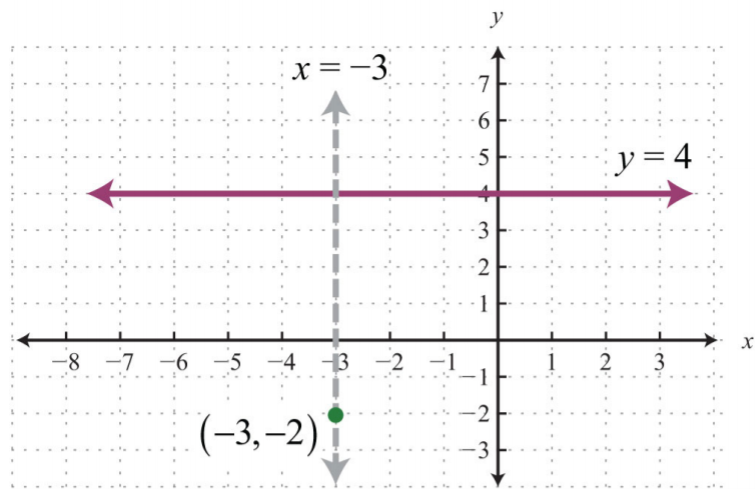
Find the equation of the line passing through $(−3, −2)$ and perpendicular to $y=4$.

Solution:

We recognize that $y=4$ is a horizontal line and we want to find a perpendicular line passing through $(−3, −2)$.

$Screenshot (632).png$

Figure $\PageIndex{5}$

If we draw the line perpendicular to the given horizontal line, the result is a vertical line.

$Screenshot (633).png$

Figure $\PageIndex{6}$

Equations of vertical lines look like $x=k$. Since it must pass through $(−3, −2)$, we conclude that $x=−3$ is the equation. All ordered pair solutions of a vertical line must share the same $x$-coordinate.

Answer:

$x=−3$

We can rewrite the equation of any horizontal line, $y=k$, in slope-intercept form as follows:

$y=0x+k$

Written in this form, we see that the slope is $m=0=\frac{0}{1}$. If we try to find the slope of a perpendicular line by finding the opposite reciprocal, we run into a problem: $m_{⊥}=−\frac{1}{0}$, which is undefined. This is why we took care to restrict the definition to two nonvertical lines. Remember that horizontal lines are perpendicular to vertical lines.

Key Takeaways

Parallel lines have the same slope.
Perpendicular lines have slopes that are opposite reciprocals. In other words, if $m=\frac{a}{b}$, then $m_{⊥}=−\frac{b}{a}$.
To find an equation of a line, first use the given information to determine the slope. Then use the slope and a point on the line to find the equation using point-slope form.
Horizontal and vertical lines are perpendicular to each other.

Exercise $\PageIndex{3}$ Parallel and Perpendicular Lines

Determine the slope of parallel lines and perpendicular lines.

$y=−\frac{3}{4}x+8$
$y=\frac{1}{2}x−3$
$y=4x+4$
$y=−3x+7$
$y=−\frac{5}{8}x−12$
$y=\frac{7}{3}x+\frac{3}{2}$
$y=9x−25$
$y=−10x+15$
$y=5$
$x=−12$
$x−y=0$
$x+y=0$
$4x+3y=0$
$3x−5y=10$
$−2x+7y=14$
$−x−y=\frac{1}{5}$
$\frac{1}{2}x−\frac{1}{3}y=−1$
$−\frac{2}{3}x+\frac{4}{5}y=8$
$2x−\frac{1}{5}y=\frac{1}{10}$
$−\frac{4}{5}x−2y=7$

Answer

1. $m_{∥}=−\frac{3}{4}$ and $m_{⊥}=\frac{4}{3}$

3. $m_{∥}=4$ and $m_{⊥}=−\frac{1}{4}$

5. $m_{∥}=−\frac{5}{8}$ and $m_{⊥}=\frac{8}{5}$

7. $m_{∥}=9$ and $m_{⊥}=−\frac{1}{9}$

9. $m_{∥}=0$ and $m_{⊥}$ undefined

11. $m_{∥}=1$ and $m_{⊥}=−1$

13. $m_{∥}=−\frac{4}{3}$ and $m_{⊥}=\frac{3}{4}$

15. $m_{∥}=\frac{2}{7}$ and $m_{⊥}=−\frac{7}{2}$

17. $m_{∥}=\frac{3}{2}$ and $m_{⊥}=−\frac{2}{3}$

19. $m_{∥}=10$ and $m_{⊥}=−\frac{1}{10}$

Exercise $\PageIndex{4}$ Parallel and Perpendicular Lines

Determine if the lines are parallel, perpendicular, or neither.

$\left\{\begin{aligned}y&=\frac{2}{3}x+3\\y&=\frac{2}{3}x−3\end{aligned}\right.$
$\left\{\begin{aligned}y&=\frac{3}{4}x−1\\y&=\frac{4}{3}x+3\end{aligned}\right.$
$\left\{\begin{aligned}y&=−2x+1\\ y&=\frac{1}{2}x+8\end{aligned}\right.$
$\left\{\begin{aligned}y&=3x−\frac{1}{2}\\ y&=3x+2\end{aligned}\right.$
$\left\{\begin{aligned}y&=5\\x&=−2\end{aligned}\right.$
$\left\{\begin{aligned}y&=7\\y&=−\frac{1}{7}\end{aligned}\right.$
$\left\{\begin{aligned}3x−5y&=15\\ 5x+3y&=9\end{aligned}\right.$
$\left\{\begin{aligned}x−y&=7\\3x+3y&=2\end{aligned}\right.$
$\left\{\begin{aligned}2x−6y&=4\\−x+3y&=−2 \end{aligned}\right.$
$\left\{\begin{aligned}−4x+2y&=3\\6x−3y&=−3 \end{aligned}\right.$
$\left\{\begin{aligned}x+3y&=9\\2x+3y&=6 \end{aligned}\right.$
$\left\{\begin{aligned}y−10&=0\\x−10&=0 \end{aligned}\right.$
$\left\{\begin{aligned}y+2&=0\\2y−10&=0 \end{aligned}\right.$
$\left\{\begin{aligned}3x+2y&=6\\2x+3y&=6 \end{aligned}\right.$
$\left\{\begin{aligned}−5x+4y&=20\\10x−8y&=16 \end{aligned}\right.$
$\left\{\begin{aligned}\frac{1}{2}x−\frac{1}{3}y&=1\\\frac{1}{6}x+\frac{1}{4}y&=−2\end{aligned}\right.$

Answer

1. Parallel

3. Perpendicular

5. Perpendicular

7. Perpendicular

9. Parallel

11. Neither

13. Parallel

15. Parallel

Exercise $\PageIndex{5}$ Equations in Point-Slope Form

Find the equation of the line

Parallel to $y=\frac{1}{2}x+2$ and passing through $(6, −1)$.
Parallel to $y=−\frac{3}{4}x−3$ and passing through $(−8, 2)$.
Perpendicular to $y=3x−1$ and passing through $(−3, 2)$.
Perpendicular to $y=−\frac{1}{3}x+2$ and passing through $(4, −3)$.
Perpendicular to $y=−2$ and passing through $(−1, 5)$.
Perpendicular to $x=\frac{1}{5}$ and passing through $(5, −3)$.
Parallel to $y=3$ and passing through $(2, 4)$.
Parallel to $x=2$ and passing through (7, −3)\).
Perpendicular to $y=x$ and passing through $(7, −13)$.
Perpendicular to $y=2x+9$ and passing through $(3, −1)$.
Parallel to $y=\frac{1}{4}x−5$ and passing through $(−2, 1)$.
Parallel to $y=−\frac{3}{4}x+1$ and passing through $(4, \frac{1}{4})$.
Parallel to $2x−3y=6$ and passing through $(6, −2)$.
Parallel to $−x+y=4$ and passing through $(9, 7)$.
Perpendicular to $5x−3y=18$ and passing through $(−9, 10)$.
Perpendicular to $x−y=11$ and passing through $(6, −8)$.
Parallel to $\frac{1}{5}x−\frac{1}{3}y=2$ and passing through $(−15, 6)$.
Parallel to $−10x−\frac{5}{7}y=12$ and passing through $(−1, \frac{1}{2})$.
Perpendicular to $\frac{1}{2}x−\frac{1}{3}y=1$ and passing through $(−10, 3)$.
Perpendicular to $−5x+y=−1$ and passing through $(−4, 0)$.
Parallel to $x+4y=8$ and passing through $(−1, −2)$.
Parallel to $7x−5y=35$ and passing through $(2, −3)$.
Perpendicular to $6x+3y=1$ and passing through $(8, −2)$.
Perpendicular to $−4x−5y=1$ and passing through $(−1, −1)$.
Parallel to $−5x−2y=4$ and passing through $(\frac{1}{5}, −\frac{1}{4})$.
Parallel to $6x−\frac{3}{2}y=9$ and passing through $(\frac{1}{3}, \frac{2}{3})$.
Perpendicular to $y−3=0$ and passing through $(−6, 12)$.
Perpendicular to $x+7=0$ and passing through $(5, −10)$.

Answer

1. $y=\frac{1}{2}x−4$

3. $y=−\frac{1}{3}x+1$

5. $x=−1$

7. $y=4$

9. $y=−x−6$

11. $y=\frac{1}{4}x+\frac{3}{2}$

13. $y=\frac{2}{3}x−6$

15. $y=−\frac{3}{5}x+\frac{23}{5}$

17. $y=\frac{3}{5}x+15$

19. $y=−\frac{2}{3}x−\frac{11}{3}$

21. $y=−\frac{1}{4}x−\frac{9}{4}$

23. $y=\frac{1}{2}x−6$

25. $y=−\frac{5}{2}x+\frac{1}{4}$

27. $x=−6$

Given slope	Slope of perpendicular line
\(m=\frac{1}{2}\)	\(m_{\perp}=-2\)
\(m=-\frac{3}{4}\)	\(m_{\perp}=\frac{4}{3}\)
\(m=3\)	\(m_{\perp}=-\frac{1}{3}\)
\(m=-4\)	\(m_{\perp}=\frac{1}{4}\)

Search

Text Color

Text Size

Margin Size

Font Type

Example \(\PageIndex{1}\)

Example \(\PageIndex{2}\)

Exercise \(\PageIndex{1}\)

Example \(\PageIndex{3}\)

Solution

Example \(\PageIndex{4}\)

Example \(\PageIndex{5}\)

Example \(\PageIndex{6}\)

Exercise \(\PageIndex{2}\)

Example \(\PageIndex{7}\)

Exercise \(\PageIndex{3}\) Parallel and Perpendicular Lines

Exercise \(\PageIndex{4}\) Parallel and Perpendicular Lines

Exercise \(\PageIndex{5}\) Equations in Point-Slope Form