6.2: Greatest Common Factor and Factor by Grouping
- Page ID
- 5153
By the end of this section, you will be able to:
- Find the greatest common factor of two or more expressions
- Factor the greatest common factor from a polynomial
- Factor by grouping
Find the Greatest Common Factor of Two or More Expressions
Earlier we multiplied factors together to get a product. Now, we will reverse this process; we will start with a product and then break it down into its factors. Splitting a product into factors is called factoring.
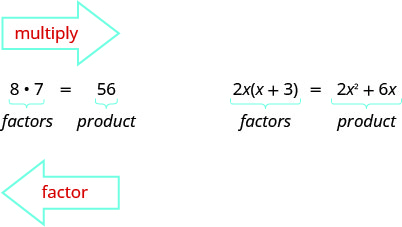
We have learned how to factor numbers to find the least common multiple (LCM) of two or more numbers. Now we will factor expressions and find the greatest common factor of two or more expressions. The method we use is similar to what we used to find the LCM.
The greatest common factor (GCF) of two or more expressions is the largest expression that is a factor of all the expressions.
We summarize the steps we use to find the greatest common factor.
- Factor each coefficient into primes. Write all variables with exponents in expanded form.
- List all factors—matching common factors in a column. In each column, circle the common factors.
- Bring down the common factors that all expressions share.
- Multiply the factors.
The next example will show us the steps to find the greatest common factor of three expressions.
Find the greatest common factor of \(21x^3,\space 9x^2,\space 15x\).
- Answer
-
Factor each coefficient into primes and write the variables with exponents in expanded form. Circle the common factors in each column. Bring down the common factors. 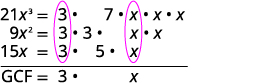
Multiply the factors. GCF \(=3x\) The GCF of \(21x^3\), \(9x^2\) and \(15x\) is \(3x\).
Find the greatest common factor: \(25m^4,\space 35m^3,\space 20m^2.\)
- Answer
-
\(5m^2\)
Find the greatest common factor: \(14x^3,\space 70x^2,\space 105x\).
- Answer
-
\(7x\)
Factor the Greatest Common Factor from a Polynomial
It is sometimes useful to represent a number as a product of factors, for example, 12 as \(2·6\) or \(3·4\). In algebra, it can also be useful to represent a polynomial in factored form. We will start with a product, such as \(3x^2+15x\), and end with its factors, \(3x(x+5)\). To do this we apply the Distributive Property “in reverse.”
We state the Distributive Property here just as you saw it in earlier chapters and “in reverse.”
If a, b, and c are real numbers, then
\[a(b+c)=ab+ac \quad \text{and} \quad ab+ac=a(b+c)\nonumber\]
The form on the left is used to multiply. The form on the right is used to factor.
So how do you use the Distributive Property to factor a polynomial? You just find the GCF of all the terms and write the polynomial as a product!
Factor: \(8m^3−12m^2n+20mn^2\).
- Answer
-




Factor: \(9xy^2+6x^2y^2+21y^3\).
- Answer
-
\(3y^2(3x+2x^2+7y)\)
Factor: \(3p^3−6p^2q+9pq^3\).
- Answer
-
\(3p(p^2−2pq+3q^3)\)
- Find the GCF of all the terms of the polynomial.
- Rewrite each term as a product using the GCF.
- Use the “reverse” Distributive Property to factor the expression.
- Check by multiplying the factors.
We use “factor” as both a noun and a verb:
\[\begin{array} {ll} \text{Noun:} &\hspace{50mm} 7 \text{ is a factor of }14 \\ \text{Verb:} &\hspace{50mm} \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
Factor: \(5x^3−25x^2\).
- Answer
-
Find the GCF of \(5x^3\) and \(25x^2\). 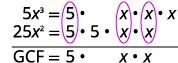
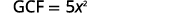
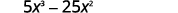
Rewrite each term. 
Factor the GCF. 
Check:
\[5x^2(x−5) \nonumber\]\[5x^2·x−5x^2·5 \nonumber\]
\[5x^3−25x^2 \checkmark\nonumber\]
Factor: \(2x^3+12x^2\).
- Answer
-
\(2x^2(x+6)\)
Factor: \(6y^3−15y^2\).
- Answer
-
\(3y^2(2y−5)\)
Factor: \(8x^3y−10x^2y^2+12xy^3\).
- Answer
-
The GCF of \(8x^3y,\space −10x^2y^2,\) and \(12xy^3\)
is \(2xy\).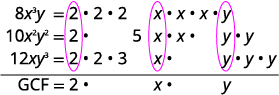

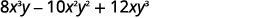
Rewrite each term using the GCF, \(2xy\). 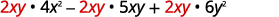
Factor the GCF. 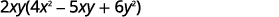
Check:
\[2xy(4x^2−5xy+6y^2)\nonumber\]\[2xy·4x^2−2xy·5xy+2xy·6y^2\nonumber\]
\[8x^3y−10x^2y^2+12xy^3\checkmark\nonumber\]
Factor: \(15x^3y−3x^2y^2+6xy^3\).
- Answer
-
\(3xy(5x^2−xy+2y^2)\)
Factor: \(8a^3b+2a^2b^2−6ab^3\).
- Answer
-
\(2ab(4a^2+ab−3b^2)\)
When the leading coefficient is negative, we factor the negative out as part of the GCF.
Factor: \(−4a^3+36a^2−8a\).
- Answer
-
The leading coefficient is negative, so the GCF will be negative.
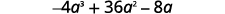
Rewrite each term using the GCF, \(−4a\). 
Factor the GCF. 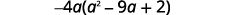
Check:
\[−4a(a^2−9a+2)\nonumber\]\[−4a·a^2−(−4a)·9a+(−4a)·2\nonumber\]
\[−4a^3+36a^2−8a\checkmark\nonumber\]
Factor: \(−4b^3+16b^2−8b\).
- Answer
-
\(−4b(b^2−4b+2)\)
Factor: \(−7a^3+21a^2−14a\).
- Answer
-
\(−7a(a^2−3a+2)\)
So far our greatest common factors have been monomials. In the next example, the greatest common factor is a binomial.
Factor: \(3y(y+7)−4(y+7)\).
- Answer
-
The GCF is the binomial \(y+7\).
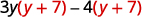
Factor the GCF, \((y+7)\). \((y+7)(3 y-4)\) Check on your own by multiplying.
Factor: \(4m(m+3)−7(m+3)\).
- Answer
-
\((m+3)(4m−7)\)
Factor: \(8n(n−4)+5(n−4)\).
- Answer
-
\((n−4)(8n+5)\)
Factor by Grouping
Sometimes there is no common factor of all the terms of a polynomial. When there are four terms we separate the polynomial into two parts with two terms in each part. Then look for the GCF in each part. If the polynomial can be factored, you will find a common factor emerges from both parts. Not all polynomials can be factored. Just like some numbers are prime, some polynomials are prime.
Factor by grouping: \(xy+3y+2x+6\).
- Answer
-




Factor by grouping: \(xy+8y+3x+24\).
- Answer
-
\((x+8)(y+3)\)
Factor by grouping: \(ab+7b+8a+56\).
- Answer
-
\((a+7)(b+8)\)
- Group terms with common factors.
- Factor out the common factor in each group.
- Factor the common factor from the expression.
- Check by multiplying the factors.
Factor by grouping: ⓐ \(x^2+3x−2x−6\) ⓑ \(6x^2−3x−4x+2\).
- Answer
-
ⓐ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &x^2+3x−2x−6 \\ \text{Separate into two parts.} &x^2+3x\quad −2x−6 \\ \begin{array} {l} \text{Factor the GCF from both parts. Be careful} \\ \text{with the signs when factoring the GCF from} \\ \text{the last two terms.} \end{array} &x(x+3)−2(x+3) \\ \text{Factor out the common factor.} &(x+3)(x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
ⓑ
\(\begin{array} {ll} \text{There is no GCF in all four terms.} &6x^2−3x−4x+2 \\ \text{Separate into two parts.} &6x^2−3x\quad −4x+2\\ \text{Factor the GCF from both parts.} &3x(2x−1)−2(2x−1) \\ \text{Factor out the common factor.} &(2x−1)(3x−2) \\ \text{Check on your own by multiplying.} & \end{array}\)
Factor by grouping: ⓐ \(x^2+2x−5x−10\) ⓑ \(20x^2−16x−15x+12\).
- Answer
-
ⓐ \((x−5)(x+2)\)
ⓑ \((5x−4)(4x−3)\)
Factor by grouping: ⓐ \(y^2+4y−7y−28\) ⓑ \(42m^2−18m−35m+15\).
- Answer
-
ⓐ \((y+4)(y−7)\)
ⓑ \((7m−3)(6m−5)\)
Key Concepts
- How to find the greatest common factor (GCF) of two expressions.
- Factor each coefficient into primes. Write all variables with exponents in expanded form.
- List all factors—matching common factors in a column. In each column, circle the common factors.
- Bring down the common factors that all expressions share.
- Multiply the factors.
- Distributive Property: If \(a\), \(b\) and \(c\) are real numbers, then
\[a(b+c)=ab+ac\quad \text{and}\quad ab+ac=a(b+c)\nonumber\]
The form on the left is used to multiply. The form on the right is used to factor. - How to factor the greatest common factor from a polynomial.
- Find the GCF of all the terms of the polynomial.
- Rewrite each term as a product using the GCF.
- Use the “reverse” Distributive Property to factor the expression.
- Check by multiplying the factors.
- Factor as a Noun and a Verb: We use “factor” as both a noun and a verb.
\[\begin{array} {ll} \text{Noun:} &\quad 7 \text{ is a factor of } 14\\ \text{Verb:} &\quad \text{factor }3 \text{ from }3a+3\end{array}\nonumber\]
- How to factor by grouping.
- Group terms with common factors.
- Factor out the common factor in each group.
- Factor the common factor from the expression.
- Check by multiplying the factors.
Glossary
- factoring
- Splitting a product into factors is called factoring.
- greatest common factor
- The greatest common factor (GCF) of two or more expressions is the largest expression that is a factor of all the expressions.


