9.5: Solve Quadratic Equations in Quadratic Form
- Page ID
- 5175
By the end of this section, you will be able to:
- Solve equations in quadratic form
... take this readiness quiz.
- Factor by substitution: \(y^{4}-y^{2}-20\).
- Factor by substitution: \((y-4)^{2}+8(y-4)+15\).
- Simplify
- \(x^{\frac{1}{2}} \cdot x^{\frac{1}{4}}\)
- \(\left(x^{\frac{1}{3}}\right)^{2}\)
- \(\left(x^{-1}\right)^{2}\)
Solve Equations in Quadratic Form
Sometimes when we factored trinomials, the trinomial did not appear to be in the \(ax^{2}+bx+c\) form. So we factored by substitution allowing us to make it fit the \(ax^{2}+bx+c\) form. We used the standard \(u\) for the substitution.
To factor the expression \(x^{4}-4 x^{2}-5\), we noticed the variable part of the middle term is \(x^{2}\) and its square, \(x^{4}\), is the variable part of the first term. (We know \(\left(x^{2}\right)^{2}=x^{4}\).) So we let \(u=x^{2}\) and factored.
| \(x^{4}-4 x^{2}-5\) | |
| \(\left(\color{red}x^2 \color{black} \right)^{2}-4\left( \color{red}x^{2} \color{black}\right)-5\) | |
| Let \(u=x^{2}\) and substitute. | \(\color{red}u \color{black}^{2}-4 \color{red}u \color{black}-5\) |
| Factor the trinomial. | \((u+1)(u-5)\) |
| Replace \(u\) with \(x^{2}\). | \(\left( \color{red}x^{2} \color{black} + 1\right)\left( \color{red}x^2 \color{black}-5\right)\) |
Similarly, sometimes an equation is not in the \(ax^{2}+bx+c=0\) form but looks much like a quadratic equation. Then, we can often make a thoughtful substitution that will allow us to make it fit the \(ax^{2}+bx+c=0\) form. If we can make it fit the form, we can then use all of our methods to solve quadratic equations.
Notice that in the quadratic equation \(ax^{2}+bx+c=0\), the middle term has a variable, \(x\), and its square, \(x^{2}\), is the variable part of the first term. Look for this relationship as you try to find a substitution.
Again, we will use the standard \(u\) to make a substitution that will put the equation in quadratic form. If the substitution gives us an equation of the form \(ax^{2}+bx+c=0\), we say the original equation was of quadratic form.
The next example shows the steps for solving an equation in quadratic form.
Solve: \(6 x^{4}-7 x^{2}+2=0\)
Solution:
| Step 1: Identify a substitution that will put the equation in quadratic form. | Since \(\left(x^{2}\right)^{2}=x^{4}\), we let \(u=x^{2}\). | \(6 x^{4}-7 x^{2}+2=0\) |
| Step 2: Rewrite the equation with the substitution to put it in quadratic form. |
Rewrite to prepare for the substitution. Substitute \(u=x^{2}\). |
\(\begin{aligned}6\color{black}{\left(\color{red}{x^{2}}\right)}^{2}-7\color{red}{ x^{2}}\color{black}{+}2&=0 \\ \color{black}{6 \color{red}{u}^{2}}-7 \color{red}{u}\color{black}{+}2&=0\end{aligned}\) |
| Step 3: Solve the quadratic equation for \(u\). |
We can solve by factoring. Use the Zero Product Property. |
\(\begin{aligned}(2 u-1)(3 u-2) &=0 \\ 2 u-1=0, 3 u-2&=0 \\ 2 u =1,3 u&=2 \\ u =\frac{1}{2} u&=\frac{2}{3} \end{aligned}\) |
| Step 4: Substitute the original variable back into the results, using the substitution. | Replace \(u\) with \(x^{2}\). | \(x^{2}=\frac{1}{2} \quad x^{2}=\frac{2}{3}\) |
| Step 5: Solve for the original variable. | Solve for \(x\), using the Square Root Property. |
\(\begin{array}{ll}{x=\pm \sqrt{\frac{1}{2}}} & {x=\pm \sqrt{\frac{2}{3}}} \\ {x=\pm \frac{\sqrt{2}}{2}} & {x=\pm \frac{\sqrt{6}}{3}}\end{array}\) There are four solutions. \(\begin{array}{ll}{x=\frac{\sqrt{2}}{2}} & {x=\frac{\sqrt{6}}{3}} \\ {x=-\frac{\sqrt{2}}{2}} & {x=-\frac{\sqrt{6}}{3}}\end{array}\) |
| Step 6: Check the solutions. | Check all four solutions. We will show one check here. |
\(\begin{aligned}x&=\frac{\sqrt{2}}{2} \\ 6 x^{4}-7 x^{2}+2&=0 \\ 6\left(\frac{\sqrt{2}}{2}\right)^{4}-7\left(\frac{\sqrt{2}}{2}\right)^{2}+2 &\stackrel{?}{=} 0\\ 6\left(\frac{4}{16} \right)-7\left(\frac{2}{4} \right)^{2}+2&\stackrel{?}{=}0 \\ \frac{3}{2}-\frac{7}{2}+\frac{4}{2}&\stackrel{?}{=}0 \\ 0&=0 \end{aligned}\) We leave the other checks to you! |
Solve: \(x^{4}-6 x^{2}+8=0\).
- Answer
-
\(x=\sqrt{2}, x=-\sqrt{2}, x=2, x=-2\)
Solve: \(x^{4}-11 x^{2}+28=0\).
- Answer
-
\(x=\sqrt{7}, x=-\sqrt{7}, x=2, x=-2\)
We summarize the steps to solve an equation in quadratic form.
- Identify a substitution that will put the equation in quadratic form.
- Rewrite the equation with the substitution to put it in quadratic form.
- Solve the quadratic equation for \(u\).
- Substitute the original variable back into the results, using the substitution.
- Solve for the original variable.
- Check the solutions.
In the next example, the binomial in the middle term, \((x-2)\) is squared in the first term. If we let \(u=x-2\) and substitute, our trinomial will be in \(a x^{2}+b x+c\) form.
Solve: \((x-2)^{2}+7(x-2)+12=0\).
Solution:
| \((x-2)^{2}+7(x-2)+12=0\) | |
| Prepare for the substitution. | \(\color{red}(x-2)\color{black}^{2}+7\color{red}(x-2) \color{black} +12=0\) |
| Let \(u=x-2\) and substitute. | \(\color{red}u^{\color{black}2} \color{black}+ 7 \color{red}u \color{black}+12=0\) |
| Solve by factoring. |
\((u+3)(u+4)=0\) \(\begin{gathered} |
|
Replace \(u\) with \(x-2\). |
\(x-2=-3, \quad x-2=-4\) |
|
Solve for \(x\). |
\(x=-1, \quad x=-2\) |
|
Check: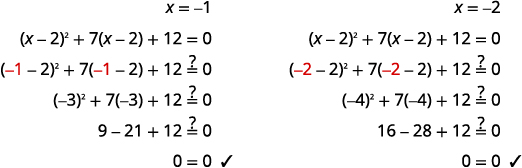 
|
Solve: \((x-5)^{2}+6(x-5)+8=0\).
- Answer
-
\(x=3, x=1\)
Solve: \((y-4)^{2}+8(y-4)+15=0\).
- Answer
-
\(y=-1, y=1\)
In the next example, we notice that \((\sqrt{x})^{2}=x\). Also, remember that when we square both sides of an equation, we may introduce extraneous roots. Be sure to check your answers!
Solve: \(x-3 \sqrt{x}+2=0\).
Solution:
The \(\sqrt{x}\) in the middle term, is squared in the first term \((\sqrt{x})^{2}=x\). If we let \(u=\sqrt{x}\) and substitute, our trinomial will be in \(a x^{2}+b x+c=0\) form.
| \(x-3 \sqrt{x}+2=0\) | |
| Rewrite the trinomial to prepare for the substitution. |  |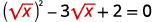
| Let \(u=\sqrt{x}\) and substitute. |  |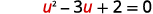
| Solve by factoring. |
\((u-2)(u-1)=0\) \(u-2=0, \quad u-1=0\) |
| Replace \(u\) with \(\sqrt{x}\). |
\(\sqrt{x}=2, \quad \sqrt{x}=1\) |
| Solve for \(x\), by squaring both sides. | \(x=4, \quad x=1\) |
|
Check:  |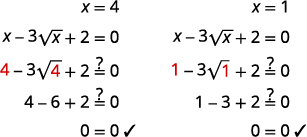
Solve: \(x-7 \sqrt{x}+12=0\).
- Answer
-
\(x=9, x=16\)
Solve: \(x-6 \sqrt{x}+8=0\).
- Answer
-
\(x=4, x=16\)
Substitutions for rational exponents can also help us solve an equation in quadratic form. Think of the properties of exponents as you begin the next example.
Solve: \(x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0\).
Solution:
The \(x^{\frac{1}{3}}\) in the middle term is squared in the first term \(\left(x^{\frac{1}{3}}\right)^{2}=x^{\frac{2}{3}}\). If we let \(u=x^{\frac{1}{3}}\) and substitute, our trinomial will be in \(a x^{2}+b x+c=0\) form.
| \(x^{\frac{2}{3}}-2 x^{\frac{1}{3}}-24=0\) | |
| Rewrite the trinomial to prepare for the substitution. |  |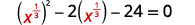
| Let \(u=x^{\frac{1}{3}}\) |  |
| Solve by factoring. |
\((u-6)(u+4)=0\) \(u-6=0, \quad u+4=0\) \(u=6, \quad u=-4\) |
| Replace \(u\) with \(x^{\frac{1}{3}}\). |
\(x^{\frac{1}{3}}=6, \quad x^{\frac{1}{3}}=-4\) |
| Solve for \(x\) by cubing both sides. |
\(\left(x^{\frac{1}{3}}\right)^{3}=(6)^{3}, \quad\left(x^{\frac{1}{3}}\right)^{3}=(-4)^{3}\) \(x=216, \quad x=-64\) |
|
Check: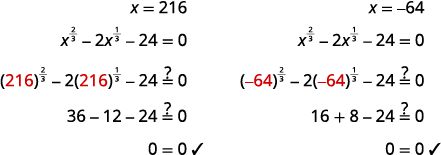 
|
Solve: \(x^{\frac{2}{3}}-5 x^{\frac{1}{3}}-14=0\).
- Answer
-
\(x=-8, x=343\)
Solve: \(x^{\frac{1}{2}}+8 x^{\frac{1}{4}}+15=0\).
- Answer
-
\(x=81, x=625\)
In the next example, we need to keep in mind the definition of a negative exponent as well as the properties of exponents.
Solve: \(3 x^{-2}-7 x^{-1}+2=0\).
Solution:
The \(x^{−1}\) in the middle term is squared in the first term \(\left(x^{-1}\right)^{2}=x^{-2}\). If we let \(u=x^{−1}\) and substitute, our trinomial will be in \(a x^{2}+b x+c=0\) form.
| \(3 x^{-2}-7 x^{-1}+2=0\) | |
| Rewrite the trinomial to prepare for the substitution. |  |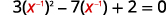
| Let \(u=x^{-1}\) and substitute. |  |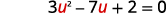
| Solve by factoring. | \((3 u-1)(u-2)=0\) |
| \(3 u-1=0, \quad u-2=0\) | |
| \(u=\frac{1}{3}, \quad u=2\) | |
| Replace \(u\) with \(x^{-1}\). | \(x^{-1}=\frac{1}{3}, \quad x^{-1}=2\) |
| Solve for \(x\) by taking the reciprocal since \(x^{-1}=\frac{1}{x}\). | \(x=3, \quad x=\frac{1}{2}\) |
|
Check: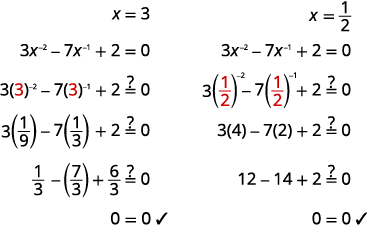 
|
Solve: \(8 x^{-2}-10 x^{-1}+3=0\).
- Answer
-
\(x=\frac{4}{3}, x=2\)
Solve: \(6 x^{-2}-23 x^{-1}+20=0\).
- Answer
-
\(x=\frac{2}{5}, x=\frac{3}{4}\)
Access this online video for additional instruction and practice with solving quadratic equations: https://www.youtube.com/watch?v=7X-CZMbpxuw
Key Concepts
- How to solve equations in quadratic form.
- Identify a substitution that will put the equation in quadratic form.
- Rewrite the equation with the substitution to put it in quadratic form.
- Solve the quadratic equation for \(u\).
- Substitute the original variable back into the results, using the substitution.
- Solve for the original variable.
- Check the solutions.