Skip to main content
\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Mathematics LibreTexts

9.7E: Graph Quadratic Functions Using Properties (Exercises)

  1. Last updated
  2. Save as PDF
  • Page ID
    30228

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Practice Makes Perfect

    Exercises 1 - 4: Recognize the Graph of a Quadratic Function

    In the following exercises, graph the functions by plotting points.

    1. \(f(x)=x^{2}+3\)

    2. \(f(x)=x^{2}-3\)

    3. \(y=-x^{2}+1\)

    4. \(f(x)=-x^{2}-1\)

    Answer

    1.

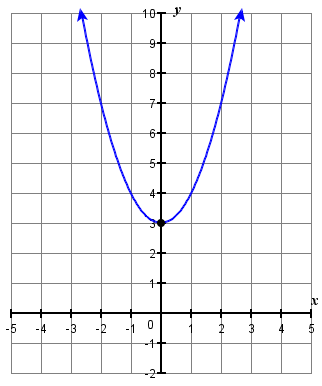
    clipboard_eb78a0f78325e7c8a9cceea709788ca1d.png

    3.

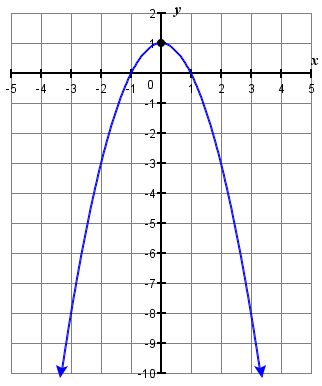
    clipboard_ef318ed788d73edacb2b69f9a778e9ce9.png

    Exercises 5 - 8: Recognize the Graph of a Quadratic Function

    For each of the following exercises, determine if the parabola opens up or down.

    5. a. \(f(x)=-2 x^{2}-6 x-7\) b. \(f(x)=6 x^{2}+2 x+3\)

    6. a. \(f(x)=4 x^{2}+x-4\) b. \(f(x)=-9 x^{2}-24 x-16\)

    7. a. \(f(x)=-3 x^{2}+5 x-1\) b. \(f(x)=2 x^{2}-4 x+5\)

    8. a. \(f(x)=x^{2}+3 x-4\) b. \(f(x)=-4 x^{2}-12 x-9\)

    Answer

    5. a. down b. up

    7. a. down b. up

    Exercises 9 - 12: Find the Axis of Symmetry and Vertex of a Parabola

    In the following functions, find

    1. The equation of the axis of symmetry
    2. The vertex of its graph

    9. \(f(x)=x^{2}+8 x-1\)

    10. \(f(x)=x^{2}+10 x+25\)

    11. \(f(x)=-x^{2}+2 x+5\)

    12. \(f(x)=-2 x^{2}-8 x-3\)

    Answer

    9. a. Axis of symmetry: \(x=-4\) b. Vertex: \((-4,-17)\)

    11. a. Axis of symmetry: \(x=1\) b. Vertex: \((1,2)\)

    Exercises 13 - 24: Find the Intercepts of a Parabola

    In the following exercises, find the intercepts of the parabola whose function is given.

    13. \(f(x)=x^{2}+7 x+6\)

    14. \(f(x)=x^{2}+10 x-11\)

    15. \(f(x)=x^{2}+8 x+12\)

    16. \(f(x)=x^{2}+5 x+6\)

    17. \(f(x)=-x^{2}+8 x-19\)

    18. \(f(x)=-3 x^{2}+x-1\)

    19. \(f(x)=x^{2}+6 x+13\)

    20. \(f(x)=x^{2}+8 x+12\)

    21. \(f(x)=4 x^{2}-20 x+25\)

    22. \(f(x)=-x^{2}-14 x-49\)

    23. \(f(x)=-x^{2}-6 x-9\)

    24. \(f(x)=4 x^{2}+4 x+1\)

    Answer

    13. \(y\)-intercept: \((0,6)\); \(x\)-intercept(s): \((-1,0), (-6,0)\)

    15. \(y\)-intercept: \((0,12)\); \(x\)-intercept(s): \((-2,0), (-6,0)\)

    17. \(y\)-intercept: \((0,-19)\); \(x\)-intercept(s): none

    19. \(y\)-intercept: \((0,13)\); \(x\)-intercept(s): none

    21. \(y\)-intercept: \((0,-16)\); \(x\)-intercept(s): \((\frac{5}{2},0)\)

    23. \(y\)-intercept: \((0,9)\); \(x\)-intercept(s): \((-3,0)\)

    Exercises 25 - 42: Graph Quadratic Functions Using Properties

    In the following exercises, graph the function by using its properties.

    25. \(f(x)=x^{2}+6 x+5\)

    26. \(f(x)=x^{2}+4 x-12\)

    27. \(f(x)=x^{2}+4 x+3\)

    28. \(f(x)=x^{2}-6 x+8\)

    29. \(f(x)=9 x^{2}+12 x+4\)

    30. \(f(x)=-x^{2}+8 x-16\)

    31. \(f(x)=-x^{2}+2 x-7\)

    32. \(f(x)=5 x^{2}+2\)

    33. \(f(x)=2 x^{2}-4 x+1\)

    34. \(f(x)=3 x^{2}-6 x-1\)

    35. \(f(x)=2 x^{2}-4 x+2\)

    36. \(f(x)=-4 x^{2}-6 x-2\)

    37. \(f(x)=-x^{2}-4 x+2\)

    38. \(f(x)=x^{2}+6 x+8\)

    39. \(f(x)=5 x^{2}-10 x+8\)

    40. \(f(x)=-16 x^{2}+24 x-9\)

    41. \(f(x)=3 x^{2}+18 x+20\)

    42. \(f(x)=-2 x^{2}+8 x-10\)

    Answer

    25.

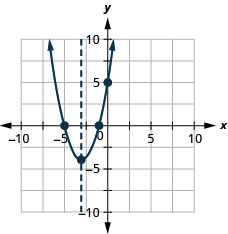
    This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (negative 3, negative 4). The y-intercept, point (0, 5), is plotted as are the x-intercepts, (negative 5, 0) and (negative 1, 0).
    Figure 9.6.136

    27.

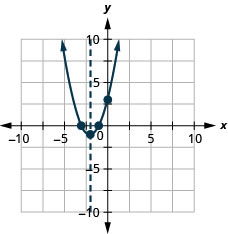
    This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (negative 2, negative 1). The y-intercept, point (0, 3), is plotted as are the x-intercepts, (negative 3, 0) and (negative 1, 0).
    Figure 9.6.137

    29.

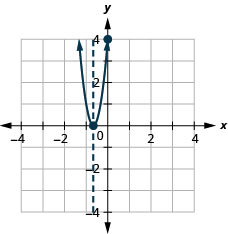
    This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 4 to 4. The y-axis of the plane runs from negative 4 to 4. The parabola has a vertex at (negative 2 thirds, 0). The y-intercept, point (0, 4), is plotted. The axis of symmetry, x equals negative 2 thirds, is plotted as a dashed vertical line.
    Figure 9.6.138

    31.

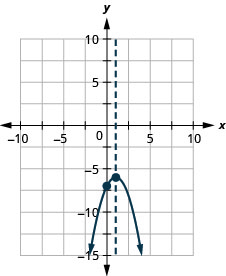
    This figure shows a downward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 15 to 10. The parabola has a vertex at (1, negative 6). The y-intercept, point (0, negative 7), is plotted. The axis of symmetry, x equals 1, is plotted as a dashed vertical line.
    Figure 9.6.139

    33.

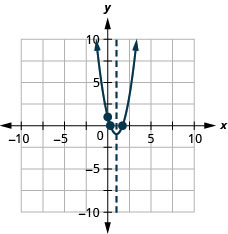
    This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (1, negative 1). The y-intercept, point (0, 1), is plotted as are the x-intercepts, approximately (0.3, 0) and (1.7, 0). The axis of symmetry is the vertical line x equals 1, plotted as a dashed line.
    Figure 9.6.140

    35.

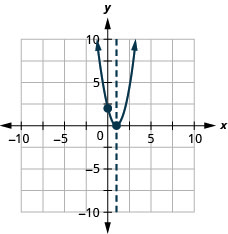
    This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (1, 0). This point is the only x-intercept. The y-intercept, point (0, 2), is plotted. The axis of symmetry is the vertical line x equals 1, plotted as a dashed line.
    Figure 9.6.141

    37.

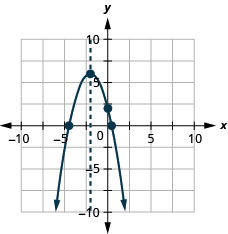
    This figure shows a downward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (negative 2, 6). The y-intercept, point (0, 2), is plotted as are the x-intercepts, approximately (negative 4.4, 0) and (0.4, 0). The axis of symmetry is the vertical line x equals 2, plotted as a dashed line.
    Figure 9.6.142

    39.

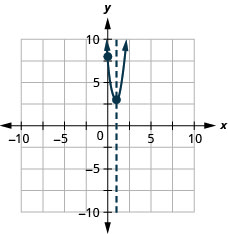
    This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (1, 3). The y-intercept, point (0, 8), is plotted; there are no x-intercepts. The axis of symmetry is the vertical line x equals 1, plotted as a dashed line.
    Figure 9.6.143

    41.

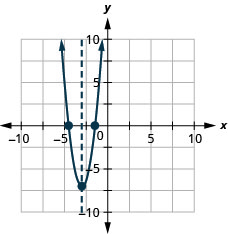
    This figure shows an upward-opening parabola graphed on the x y-coordinate plane. The x-axis of the plane runs from negative 10 to 10. The y-axis of the plane runs from negative 10 to 10. The parabola has a vertex at (negative 3, negative 7). The x-intercepts are plotted at the approximate points (negative 4.5, 0) and (negative 1.5, 0). The axis of symmetry is the vertical line x equals negative 3, plotted as a dashed line.
    Figure 9.6.144
    Exercises 43 - 48: Solve Maximum and Minimum Applications

    In the following exercises, find the maximum or minimum value of each function.

    43. \(f(x)=2 x^{2}+x-1\)

    44. \(y=-4 x^{2}+12 x-5\)

    45. \(y=x^{2}-6 x+15\)

    46. \(y=-x^{2}+4 x-5\)

    47. \(y=-9 x^{2}+16\)

    48. \(y=4 x^{2}-49\)

    Answer

    43. The minimum value is \(−\frac{9}{8}\) when \(x=−\frac{1}{4}\).

    45. The maximum value is \(6\) when \(x=3\).

    47. The maximum value is \(16\) when \(x=0\).

    Exercises 49 - 60: Solve Maximum and Minimum Applications

    In the following exercises, solve. Round answers to the nearest tenth.

    49. An arrow is shot vertically upward from a platform \(45\) feet high at a rate of \(168\) ft/sec. Use the quadratic function \(h(t)=-16 t^{2}+168 t+45\) find how long it will take the arrow to reach its maximum height, and then find the maximum height.

    50. A stone is thrown vertically upward from a platform that is \(20\) feet height at a rate of \(160\) ft/sec. Use the quadratic function \(h(t)=-16 t^{2}+160 t+20\) to find how long it will take the stone to reach its maximum height, and then find the maximum height.

    51. A ball is thrown vertically upward from the ground with an initial velocity of \(109\) ft/sec. Use the quadratic function \(h(t)=-16 t^{2}+109 t+0\) to find how long it will take for the ball to reach its maximum height, and then find the maximum height.

    52. A ball is thrown vertically upward from the ground with an initial velocity of \(122\) ft/sec. Use the quadratic function \(h(t)=-16 t^{2}+122 t+0\) to find how long it will take for the ball to reach its maximum height, and then find the maximum height.

    53. A computer store owner estimates that by charging \(x\) dollars each for a certain computer, he can sell \(40 − x\) computers each week. The quadratic function \(R(x)=-x^{2}+40 x\) is used to find the revenue, \(R\), received when the selling price of a computer is \(x\), Find the selling price that will give him the maximum revenue, and then find the amount of the maximum revenue.

    54. A retailer who sells backpacks estimates that by selling them for \(x\) dollars each, he will be able to sell \(100 − x\) backpacks a month. The quadratic function \(R(x)=-x^{2}+100 x\) is used to find the \(R\), received when the selling price of a backpack is \(x\). Find the selling price that will give him the maximum revenue, and then find the amount of the maximum revenue.

    55. A retailer who sells fashion boots estimates that by selling them for \(x\) dollars each, he will be able to sell \(70 − x\) boots a week. Use the quadratic function \(R(x)=-x^{2}+70 x\) to find the revenue received when the average selling price of a pair of fashion boots is \(x\). Find the selling price that will give him the maximum revenue, and then find the amount of the maximum revenue per day.

    56. A cell phone company estimates that by charging \(x\) dollars each for a certain cell phone, they can sell \(8 − x\) cell phones per day. Use the quadratic function \(R(x)=-x^{2}+8 x\) to find the revenue received per day when the selling price of a cell phone is \(x\). Find the selling price that will give them the maximum revenue per day, and then find the amount of the maximum revenue.

    57. A rancher is going to fence three sides of a corral next to a river. He needs to maximize the corral area using \(240\) feet of fencing. The quadratic equation \(A(x)=x(240-2 x)\) gives the area of the corral, \(A\), for the length, \(x\), of the corral along the river. Find the length of the corral along the river that will give the maximum area, and then find the maximum area of the corral.

    58. A veterinarian is enclosing a rectangular outdoor running area against his building for the dogs he cares for. He needs to maximize the area using \(100\) feet of fencing. The quadratic function \(A(x)=x(100-2 x)\) gives the area, \(A\), of the dog run for the length, \(x\), of the building that will border the dog run. Find the length of the building that should border the dog run to give the maximum area, and then find the maximum area of the dog run.

    59. A land owner is planning to build a fenced in rectangular patio behind his garage, using his garage as one of the “walls.” He wants to maximize the area using \(80\) feet of fencing. The quadratic function \(A(x)=x(80-2 x)\) gives the area of the patio, where \(x\) is the width of one side. Find the maximum area of the patio.

    60. A family of three young children just moved into a house with a yard that is not fenced in. The previous owner gave them \(300\) feet of fencing to use to enclose part of their backyard. Use the quadratic function \(A(x)=x(300-2 x)\) to determine the maximum area of the fenced in yard.

    Answer

    49. In \(5.3\) sec the arrow will reach maximum height of \(486\) ft.

    51. In \(3.4\) seconds the ball will reach its maximum height of \(185.6\) feet.

    53. \(20\) computers will give the maximum of $\(400\) in receipts.

    55. He will be able to sell \(35\) pairs of boots at the maximum revenue of $\(1,225\).

    57. The length of the side along the river of the corral is \(120\) feet and the maximum area is \(7,200\) square feet.

    59. The maximum area of the patio is \(800\) feet.

    Exercises 61 - 64: Writing Exercises

    61. How do the graphs of the functions \(f(x)=x^{2}\) and \(f(x)=x^{2}−1\) differ? We graphed them at the start of this section. What is the difference between their graphs? How are their graphs the same?

    62. Explain the process of finding the vertex of a parabola.

    63. Explain how to find the intercepts of a parabola.

    64. How can you use the discriminant when you are graphing a quadratic function?

    Answer

    1. Answers will vary.

    3. Answers will vary.

    Self Check

    a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

    This table provides a checklist to evaluate mastery of the objectives of this section. Choose how would you respond to the statement “I can recognize the graph of a quadratic equation.” “Confidently,” “with some help,” or “No, I don’t get it.” Choose how would you respond to the statement “I can find the axis of symmetry and vertex of a parabola.” “Confidently,” “with some help,” or “No, I don’t get it.” Choose how would you respond to the statement “I can find the intercepts of a parabola.” “Confidently,” “with some help,” or “No, I don’t get it.” Choose how would you respond to the statement “I can graph quadratic equations in two variables.” “Confidently,” “with some help,” or “No, I don’t get it.” Choose how would you respond to the statement “I can solve maximum and minimum applications.” “Confidently,” “with some help,” or “No, I don’t get it.”
    Figure 9.6.145

    b. After looking at the checklist, do you think you are well-prepared for the next section? Why or why not?

    9.7E: Graph Quadratic Functions Using Properties (Exercises) is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to conform to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.