Skip to main content
\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)
Mathematics LibreTexts

9.9E: Exercises

  1. Last updated
  2. Save as PDF
  • Page ID
    30567

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Practice Makes Perfect

    Exercise \(\PageIndex{11}\) Solve Quadratic Inequalities Graphically

    In the following exercises,

    1. Solve graphically
    2. Write the solution in interval notation
      1. \(x^{2}+6 x+5>0\)
      2. \(x^{2}+4 x-12<0\)
      3. \(x^{2}+4 x+3 \leq 0\)
      4. \(x^{2}-6 x+8 \geq 0\)
      5. \(-x^{2}-3 x+18 \leq 0\)
      6. \(-x^{2}+2 x+24<0\)
      7. \(-x^{2}+x+12 \geq 0\)
      8. \(-x^{2}+2 x+15>0\)
    Answer

    1.


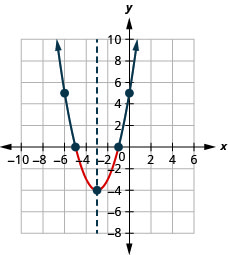
    1. The graph shown is an upward-facing parabola with vertex (negative 3, negative 4) and y-intercept (0,5).
      Figure 9.8.16
    2. \((-\infty,-5) \cup(-1, \infty)\)

    3.


    1. The graph shown is an upward facing parabola with vertex (negative 2, negative 1) and y-intercept (0,3).
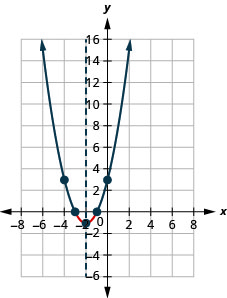
      Figure 9.8.17
    2. \([-3,-1]\)

    5.


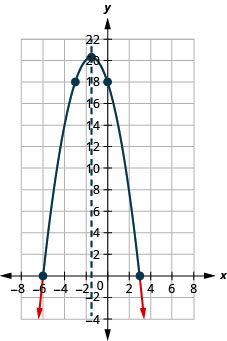
    1. The graph shown is a downward-facing parabola with vertex (negative 1 and 5 tenths, 20) and y-intercept (0, 18).
      Figure 9.8.18
    2. \((-\infty,-6] \cup[3, \infty)\)

    7.


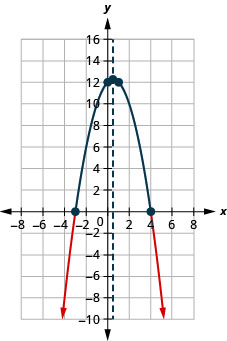
    1. The graph shown is a downward facing parabola with a y-intercept of (0, 12) and x-intercepts (negative 3, 0) and (4, 0).
      Figure 9.8.19
    2. \([-3,4]\)
    Exercise \(\PageIndex{12}\) Solve Quadratic Inequalities Graphically

    In the following exercises, solve each inequality algebraically and write any solution in interval notation.

    1. \(x^{2}+3 x-4 \geq 0\)
    2. \(x^{2}+x-6 \leq 0\)
    3. \(x^{2}-7 x+10<0\)
    4. \(x^{2}-4 x+3>0\)
    5. \(x^{2}+8 x>-15\)
    6. \(x^{2}+8 x<-12\)
    7. \(x^{2}-4 x+2 \leq 0\)
    8. \(-x^{2}+8 x-11<0\)
    9. \(x^{2}-10 x>-19\)
    10. \(x^{2}+6 x<-3\)
    11. \(-6 x^{2}+19 x-10 \geq 0\)
    12. \(-3 x^{2}-4 x+4 \leq 0\)
    13. \(-2 x^{2}+7 x+4 \geq 0\)
    14. \(2 x^{2}+5 x-12>0\)
    15. \(x^{2}+3 x+5>0\)
    16. \(x^{2}-3 x+6 \leq 0\)
    17. \(-x^{2}+x-7>0\)
    18. \(-x^{2}-4 x-5<0\)
    19. \(-2 x^{2}+8 x-10<0\)
    20. \(-x^{2}+2 x-7 \geq 0\)
    Answer

    1. \((-\infty,-4] \cup[1, \infty)\)

    3. \((2,5)\)

    5. \((-\infty,-5) \cup(-3, \infty)\)

    7. \([2-\sqrt{2}, 2+\sqrt{2}]\)

    9. \((-\infty, 5-\sqrt{6}) \cup(5+\sqrt{6}, \infty)\)

    11. \(\left(-\infty,-\frac{5}{2}\right] \cup\left[-\frac{2}{3}, \infty\right)\)

    13. \(\left[-\frac{1}{2}, 4\right]\)

    15. \((-\infty, \infty)\)

    17. no solution

    19. \((-\infty, \infty)\)

    Exercise \(\PageIndex{13}\) Writing Exercises
    1. Explain critical points and how they are used to solve quadratic inequalities algebraically.
    2. Solve \(x^{2}+2x≥8\) both graphically and algebraically. Which method do you prefer, and why?
    3. Describe the steps needed to solve a quadratic inequality graphically.
    4. Describe the steps needed to solve a quadratic inequality algebraically.
    Answer

    1. Answers may vary.

    3. Answers may vary.

    Self Check

    a. After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.

    This figure is a list to assess your understanding of the concepts presented in this section. It has 4 columns labeled I can…, Confidently, With some help, and No-I don’t get it! Below I can…, there is solve quadratic inequalities graphically and solve quadratic inequalities algebraically. The other columns are left blank for you to check you understanding.
    Figure 9.8.20

    b. On a scale of 1-10, how would you rate your mastery of this section in light of your responses on the checklist? How can you improve this?

    9.9E: Exercises is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to conform to the style and standards of the LibreTexts platform; a detailed edit history is available upon request.