Chapter 10 Review Exercises
- Page ID
- 18828
Chapter Review Exercises
Finding Composite and Inverse Functions
In the following exercises, for each pair of functions, find
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
1. \(f(x)=7 x-2\) and \(g(x)=5 x+1\)
2. \(f(x)=4 x\) and \(g(x)=x^{2}+3 x\)
- Answer
-
2.
- \(4 x^{2}+12 x\)
- \(16 x^{2}+12 x\)
- \(4 x^{3}+12 x^{2}\)
In the following exercises, evaluate the composition.
- For functions \(f(x)=3 x^{2}+2\) and \(g(x)=4 x-3\), find
- \((f \circ g)(-3)\)
- \((g \circ f)(-2)\)
- \((f \circ f)(-1)\)
- For functions \(f(x)=2 x^{3}+5\) and \(g(x)=3 x^{2}-7\), find
- \((f \circ g)(-1)\)
- \((g \circ f)(-2)\)
- \((g \circ g)(1)\)
- Answer
-
2.
- \(-123\)
- \(356\)
- \(41\)
In the following exercises, for each set of ordered pairs, determine if it represents a function and if so, is the function one-to-one.
- \(\begin{array}{l}{\{(-3,-5),(-2,-4),(-1,-3),(0,-2)} , {(-1,-1),(-2,0),(-3,1) \}}\end{array}\)
- \(\begin{array}{l}{\{(-3,0),(-2,-2),(-1,0),(0,1)} , {(1,2),(2,1),(3,-1) \}}\end{array}\)
- \(\begin{array}{l}{\{(-3,3),(-2,1),(-1,-1),(0,-3)} , {(1,-5),(2,-4),(3,-2) \}}\end{array}\)
- Answer
-
2. Function; not one-to-one
In the following exercises, determine whether each graph is the graph of a function and if so, is it one-to-one.
-
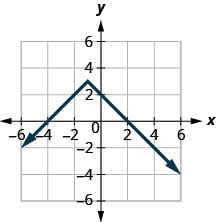
Figure 10.E.1
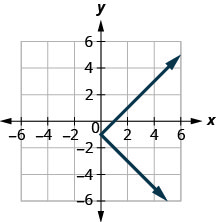
Figure 10.E.2
-
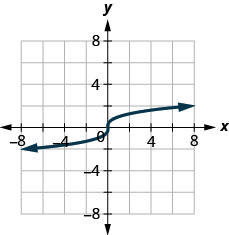
Figure 10.E.3
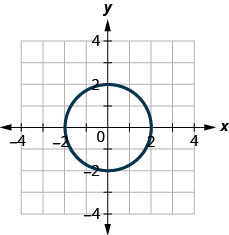
Figure 10.E.4
- Answer
-
1.
- Function; not one-to-one
- Not a function
In the following exercise, find the inverse of the function. Determine the domain and range of the inverse function.
- \(\{(-3,10),(-2,5),(-1,2),(0,1)\}\)
- Answer
-
1. Inverse function: \(\{(10,-3),(5,-2),(2,-1),(1,0)\}\). Domain: \(\{1,2,5,10\}\). Range: \(\{-3,-2,-1,0\}\).
In the following exercise, graph the inverse of the one-to-one function shown.
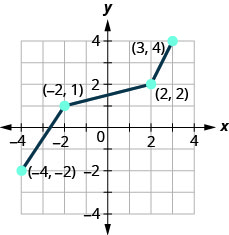
- Answer
-
Solve on your own
In the following exercises, verify that the functions are inverse functions.
- \(\begin{array}{l}{f(x)=3 x+7 \text { and }} {g(x)=\frac{x-7}{3}}\end{array}\)
- \(\begin{array}{l}{f(x)=2 x+9 \text { and }} {g(x)=\frac{x+9}{2}}\end{array}\)
- Answer
-
1. \(g(f(x))=x,\) and \(f(g(x))=x,\) so they are inverses.
- \(f(x)=6 x-11\)
- \(f(x)=x^{3}+13\)
- \(f(x)=\frac{1}{x+5}\)
- \(f(x)=\sqrt[5]{x-1}\)
- Answer
-
1. \(f^{-1}(x)=\frac{x+11}{6}\)
3. \(f^{-1}(x)=\frac{1}{x}-5\)
Evaluate and Graph Exponential Functions
In the following exercises, graph each of the following functions.
- \(f(x)=4^{x}\)
- \(f(x)=\left(\frac{1}{5}\right)^{x}\)
- \(g(x)=(0.75)^{x}\)
- \(g(x)=3^{x+2}\)
- \(f(x)=(2.3)^{x}-3\)
- \(f(x)=e^{x}+5\)
- \(f(x)=-e^{x}\)
- Answer
-
1.
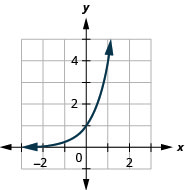
Figure 10.E.6 3.
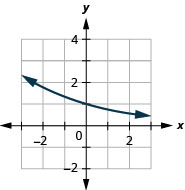
Figure 10.E.7 5.
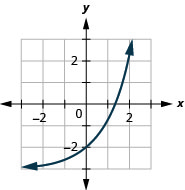
Figure 10.E.8 7.
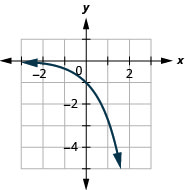
Figure 10.E.9
In the following exercises, solve each equation.
- \(3^{5 x-6}=81\)
- \(2^{x^{2}}=16\)
- \(9^{x}=27\)
- \(5^{x^{2}+2 x}=\frac{1}{5}\)
- \(e^{4 x} \cdot e^{7}=e^{19}\)
- \(\frac{e^{x^{2}}}{e^{15}}=e^{2 x}\)
- Answer
-
2. \(x=-2, x=2\)
4. \(x=-1\)
6. \(x=-3, x=5\)
In the following exercises, solve.
- Felix invested $\(12,000\) in a savings account. If the interest rate is \(4\)% how much will be in the account in \(12\) years by each method of compounding?
- compound quarterly
- compound monthly
- compound continuously
- Sayed deposits $\(20,000\) in an investment account. What will be the value of his investment in \(30\) years if the investment is earning \(7\)% per year and is compounded continuously?
- A researcher at the Center for Disease Control and Prevention is studying the growth of a bacteria. She starts her experiment with \(150\) of the bacteria that grows at a rate of \(15\)% per hour. She will check on the bacteria every \(24\) hours. How many bacteria will he find in \(24\) hours?
- In the last five years the population of the United States has grown at a rate of \(0.7\)% per year to about \(318,900,000\). If this rate continues, what will be the population in \(5\) more years?
- Answer
-
2. \(\$ 163,323.40\)
4. \(330,259,000\)
Evaluate and Graph Logarithmic Functions
In the following exercises, convert from exponential to logarithmic form.
- \(5^{4}=625\)
- \(10^{-3}=\frac{1}{1,000}\)
- \(63^{\frac{1}{5}}=\sqrt[5]{63}\)
- \(e^{y}=16\)
- Answer
-
2. \(\log \frac{1}{1,000}=-3\)
4. \(\ln 16=y\)
In the following exercises, convert each logarithmic equation to exponential form.
- \(7=\log _{2} 128\)
- \(5=\log 100,000\)
- \(4=\ln x\)
- Answer
-
2. \(100000=10^{5}\)
In the following exercises, solve for \(x\).
- \(\log _{x} 125=3\)
- \(\log _{7} x=-2\)
- \(\log _{\frac{1}{2}} \frac{1}{16}=x\)
- Answer
-
1. \(x=5\)
3. \(x=4\)
In the following exercises, find the exact value of each logarithm without using a calculator.
- \(\log _{2} 32\)
- \(\log _{8} 1\)
- \(\log _{3} \frac{1}{9}\)
- Answer
-
2. \(0\)
In the following exercises, graph each logarithmic function.
- \(y=\log _{5} x\)
- \(y=\log _{\frac{1}{4}} x\)
- \(y=\log _{0.8} x\)
- Answer
-
1.
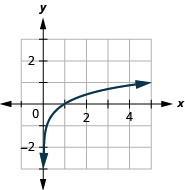
Figure 10.E.10 3.
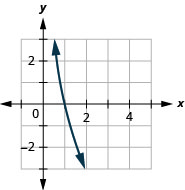
Figure 10.E.11
In the following exercises, solve each logarithmic equation.
- \(\log _{a} 36=5\)
- \(\ln x=-3\)
- \(\log _{2}(5 x-7)=3\)
- \(\ln e^{3 x}=24\)
- \(\log \left(x^{2}-21\right)=2\)
- Answer
-
2. \(x=e^{-3}\)
4. \(x=8\)
What is the decibel level of a train whistle with intensity \(10^{−3}\) watts per square inch?
- Answer
-
\(90\) dB
Use the Properties of Logarithms
In the following exercises, use the properties of logarithms to evaluate.
-
- \(\log _{7} 1\)
- \(\log _{12} 12\)
-
- \(5^{\log _{5} 13}\)
- \(\log _{3} 3^{-9}\)
-
- \(10^{\log \sqrt{5}}\)
- \(\log 10^{-3}\)
-
- \(e^{\ln 8}\)
- \(\ln e^{5}\)
- Answer
-
2.
- \(13\)
- \(-9\)
4.
- \(8\)
- \(5\)
In the following exercises, use the Product Property of Logarithms to write each logarithm as a sum of logarithms. Simplify if possible.
- \(\log _{4}(64 x y)\)
- \(\log 10,000 m\)
- Answer
-
2. \(4+\log m\)
In the following exercises, use the Quotient Property of Logarithms to write each logarithm as a sum of logarithms. Simplify, if possible.
- \(\log _{7} \frac{49}{y}\)
- \(\ln \frac{e^{5}}{2}\)
- Answer
-
2. \(5-\ln 2\)
In the following exercises, use the Power Property of Logarithms to expand each logarithm. Simplify, if possible.
- \(\log x^{-9}\)
- \(\log _{4} \sqrt[7]{z}\)
- Answer
-
2. \(\frac{1}{7} \log _{4} z\)
In the following exercises, use properties of logarithms to write each logarithm as a sum of logarithms. Simplify if possible.
- \(\log _{3}\left(\sqrt{4} x^{7} y^{8}\right)\)
- \(\log _{5} \frac{8 a^{2} b^{6} c}{d^{3}}\)
- \(\ln \frac{\sqrt{3 x^{2}-y^{2}}}{z^{4}}\)
- \(\log _{6} \sqrt[3]{\frac{7 x^{2}}{6 y^{3} z^{5}}}\)
- Answer
-
2. \(\begin{array}{l}{\log _{5} 8+2 \log _{5} a+6 \log _{5} b} {+\log _{5} c-3 \log _{5} d}\end{array}\)
4. \(\begin{array}{l}{\frac{1}{3}\left(\log _{6} 7+2 \log _{6} x-1-3 \log _{6} y\right.} {-5 \log _{6} z )}\end{array}\)
In the following exercises, use the Properties of Logarithms to condense the logarithm. Simplify if possible.
- \(\log _{2} 56-\log _{2} 7\)
- \(3 \log _{3} x+7 \log _{3} y\)
- \(\log _{5}\left(x^{2}-16\right)-2 \log _{5}(x+4)\)
- \(\frac{1}{4} \log y-2 \log (y-3)\)
- Answer
-
2. \(\log _{3} x^{3} y^{7}\)
4. \(\log \frac{\sqrt[4]{y}}{(y-3)^{2}}\)
In the following exercises, rounding to three decimal places, approximate each logarithm.
- \(\log _{5} 97\)
- \(\log _{\sqrt{3}} 16\)
- Answer
-
2. \(5.047\)
Solve Exponential and Logarithmic Equations
In the following exercises, solve for \(x\).
- \(3 \log _{5} x=\log _{5} 216\)
- \(\log _{2} x+\log _{2}(x-2)=3\)
- \(\log (x-1)-\log (3 x+5)=-\log x\)
- \(\log _{4}(x-2)+\log _{4}(x+5)=\log _{4} 8\)
- \(\ln (3 x-2)=\ln (x+4)+\ln 2\)
- Answer
-
2. \(x=4\)
4. \(x=3\)
In the following exercises, solve each exponential equation. Find the exact answer and then approximate it to three decimal places.
- \(2^{x}=101\)
- \(e^{x}=23\)
- \(\left(\frac{1}{3}\right)^{x}=7\)
- \(7 e^{x+3}=28\)
- \(e^{x-4}+8=23\)
- Answer
-
1. \(x=\frac{\log 101}{\log 2} \approx 6.658\)
3. \(x=\frac{\log 7}{\log \frac{1}{3}} \approx-1.771\)
5. \(x=\ln 15+4 \approx 6.708\)
- Jerome invests $\(18,000\) at age \(17\). He hopes the investments will be worth $\(30,000\) when he turns \(26\). If the interest compounds continuously, approximately what rate of growth will he need to achieve his goal? Is that a reasonable expectation?
- Elise invests $\(4500\) in an account that compounds interest monthly and earns \(6\)%.How long will it take for her money to double?
- Researchers recorded that a certain bacteria population grew from \(100\) to \(300\) in \(8\) hours. At this rate of growth, how many bacteria will there be in \(24\) hours?
- Mouse populations can double in \(8\) months \(\left(A=2 A_{0}\right)\). How long will it take for a mouse population to triple?
- The half-life of radioactive iodine is \(60\) days. How much of a \(50\) mg sample will be left in \(40\) days?
- Answer
-
2. \(11.6\) years
4. \(12.7\) months
Practice Test
- For the functions, \(f(x)=6x+1\) and \(g(x)=8x−3\), find
- \((f \circ g)(x)\)
- \((g \circ f)(x)\)
- \((f \cdot g)(x)\)
- Determine if the following set of ordered pairs represents a function and if so, is the function one-to-one. \(\{(-2,2),(-1,-3),(0,1),(1,-2),(2,-3)\}\)
- Determine whether each graph is the graph of a function and if so, is it one-to-one.
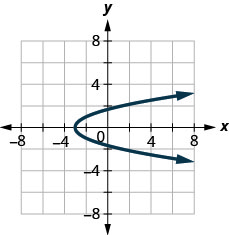
Figure 10.E.12
Figure 10.E.13
- Graph, on the same coordinate system, the inverse of the one-to-one function shown.
5. Find the inverse of the function \(f(x)=x^{5}−9\).
6. Graph the function \(g(x)=2^{x-3}\).
7. Solve the equation \(2^{2 x-4}=64\).
8. Solve the equation \(\frac{e^{x^{2}}}{e^{4}}=e^{3 x}\).
9. Megan invested $\(21,000\) in a savings account. If the interest rate is \(5\)%, how much will be in the account in \(8\) years by each method of compounding?
- compound quarterly
- compound monthly
- compound continuously
10. Convert the equation from exponential to logarithmic form: \(10^{-2}=\frac{1}{100}\).
11. Convert the equation from logarithmic equation to exponential form: \(3=\log _{7} 343\).
12. Solve for \(x\): \(\log _{5} x=-3\)
13. Evaluate log \(_{11} 1\).
14. Evaluate \(\log _{4} \frac{1}{64}\).
15. Graph the function \(y=\log _{3} x\).
16. Solve for \(x\): \(\log \left(x^{2}-39\right)=1\)
17. What is the decibel level of a small fan with intensity \(10^{−8}\) watts per square inch?
18. Evaluate each.
- \(6^{\log _{6} 17}\)
- \(\log _{9} 9^{-3}\)
- Answer
-
1.
- \(48 x-17\)
- \(48 x+5\)
- \(48 x^{2}-10 x-3\)
3.
- Not a function
- One-to-one function
5. \(f^{-1}(x)=\sqrt[5]{x+9}\)
7. \(x=5\)
9.
- $\(31,250.74\)
- $\(31,302.29\)
- $\(31,328.32\)
11. \(343=7^{3}\)
13. \(0\)
15.
Figure 10.E.15 17. \(40\) dB
In the following exercises, use properties of logarithms to write each expression as a sum of logarithms, simplifying if possible.
- \(\log _{5} 25 a b\)
- \(\ln \frac{e^{12}}{8}\)
- \(\log _{2} \sqrt[4]{\frac{5 x^{3}}{16 y^{2} z^{7}}}\)
- Answer
-
1. \(2+\log _{5} a+\log _{5} b\)
3. \(\begin{array}{l}{\frac{1}{4}\left(\log _{2} 5+3 \log _{2} x-4-2 \log _{2} y\right.} {-7 \log _{2} z )}\end{array}\)
In the following exercises, use the Properties of Logarithms to condense the logarithm, simplifying if possible.
- \(5 \log _{4} x+3 \log _{4} y\)
- \(\frac{1}{6} \log x-3 \log (x+5)\)
- Rounding to three decimal places, approximate \(\log _{4} 73\).
- Solve for \(x\): \(\log _{7}(x+2)+\log _{7}(x-3)=\log _{7} 24\)
- Answer
-
2. \(\log \frac{\sqrt[6]{x}}{(x+5)^{3}}\)
4. \(x=6\)
In the following exercises, solve each exponential equation. Find the exact answer and then approximate it to three decimal places.
- \(\left(\frac{1}{5}\right)^{x}=9\)
- \(5 e^{x-4}=40\)
- Jacob invests $\(14,000\) in an account that compounds interest quarterly and earns \(4\)%. How long will it take for his money to double?
- Researchers recorded that a certain bacteria population grew from \(500\) to \(700\) in \(5\) hours. At this rate of growth, how many bacteria will there be in \(20\) hours?
- A certain beetle population can double in \(3\) months \(\left(A=2 A_{0}\right)\). How long will it take for that beetle population to triple?
- Answer
-
2. \(x=\ln 8+4 \approx 6.079\)
4. \(1,921\) bacteria


