12.4: Geometric Sequences and Series
- Page ID
- 5197
By the end of this section, you will be able to:
- Determine if a sequence is geometric
- Find the general term (\(n\)th term) of a geometric sequence
- Find the sum of the first \(n\) terms of a geometric sequence
- Find the sum of an infinite geometric series
- Apply geometric sequences and series in the real world
Before you get started, take this readiness quiz.
- Simplify: \(\frac{24}{32}\).
If you missed this problem, review Example 1.24. - Evaluate: a. \(3^{4}\) b. \(\left(\frac{1}{2}\right)^{4}\).
If you missed this problem, review Example 1.19. - If \(f(x)=4 \cdot 3^{x}\), find a. \(f(1)\) b. \(f(2)\) c. \(f(3)\).
If you missed this problem, review Example 3.49.
Determine if a Sequence is Geometric
We are now ready to look at the second special type of sequence, the geometric sequence.
A sequence is called a geometric sequence if the ratio between consecutive terms is always the same. The ratio between consecutive terms in a geometric sequence is \(r\), the common ratio, where \(n\) is greater than or equal to two.
A geometric sequence is a sequence where the ratio between consecutive terms is always the same.
The ratio between consecutive terms, \(\frac{a_{n}}{a_{n-1}}\), is \(r\), the common ratio. \(n\) is greater than or equal to two.
Consider these sequences.
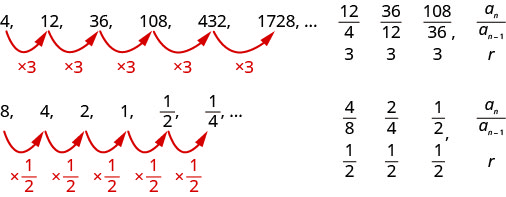
Determine if each sequence is geometric. If so, indicate the common ratio.
- \(4,8,16,32,64,128, \dots\)
- \(-2,6,-12,36,-72,216, \dots\)
- \(27,9,3,1, \frac{1}{3}, \frac{1}{9}, \ldots\)
Solution:
To determine if the sequence is geometric, we find the ratio of the consecutive terms shown.
a. Find the ratio of the consecutive terms
\(\begin{aligned} 4, \quad& \:8, \quad 16, \quad 32, \quad 64, \quad 128, \dots \\ &\frac{8}{4} \quad\frac{16}{8}\quad\frac{32}{16}\quad\frac{64}{32}\quad\frac{128}{64} \\ &\:2 \quad\:\:\: 2 \quad\quad2\quad\quad2\quad\quad2 \end{aligned}\)
The sequence is geometric. The common ration is \(r=2\).
b. Find the ratio of the consecutive terms
\(\begin{aligned}-\:2,\quad &\:\:\:6,\quad -12,\quad 36,\quad \:-72\quad \:\:216,\dots \\ & \frac{6}{-2}\quad\frac{-12}{6}\quad\frac{36}{-12}\quad\frac{-72}{36}\quad\frac{216}{-72} \\ & -3\quad -2\quad\:\: -3\quad \:\:\:-2\quad \:\:-3 \end{aligned}\)
The sequence is not geometric. There is no common ratio.
c. Find the ratio of the consecutive terms
\(\begin{aligned}27,\quad &\:\:9,\quad 3,\quad 1,\quad \frac{1}{3},\quad \frac{1}{9}, \ldots\\ & \frac{9}{27}\quad\frac{3}{9}\quad\frac{1}{3}\quad\frac{\frac{1}{3}}{1}\quad\frac{\frac{1}{9}}{\frac{1}{3}}\\ &\frac{1}{3}\quad\;\:\frac{1}{3}\quad\frac{1}{3}\quad\:\frac{1}{3}\quad\:\frac{1}{3}\end{aligned}\)
The sequence is geometric. The common ratio is \(r=\frac{1}{3}\).
Determine if each sequence is geometric. If so indicate the common ratio.
- \(7,21,63,189,567,1,701, \dots\)
- \(64,16,4,1, \frac{1}{4}, \frac{1}{16}, \dots\)
- \(2,4,12,48,240,1,440, \dots\)
- Answer
-
- The sequence is geometric with common ratio \(r=3\).
- The sequence is geometric with common ratio \(d=\frac{1}{4}\).
- The sequence is not geometric. There is no common ratio.
Determine if each sequence is geometric. If so indicate the common ratio.
- \(-150,-30,-15,-5,-\frac{5}{2}, 0, \dots\)
- \(5,10,20,40,80,160, \dots\)
- \(8,4,2,1, \frac{1}{2}, \frac{1}{4}, \ldots\)
- Answer
-
- The sequence is not geometric. There is no common ratio.
- The sequence is geometric with common ratio \(r=2\).
- The sequence is geometric with common ratio \(r=\frac{1}{2}\).
If we know the first term, \(a_{1}\), and the common ratio, \(r\), we can list a finite number of terms of the sequence.
Write the first five terms of the sequence where the first term is \(3\) and the common ratio is \(r=−2\).
Solution:
We start with the first term and multiply it by the common ratio. Then we multiply that result by the common ratio to get the next term, and so on.
\(\begin{array}{cccc}{a_{1}} & {a_{2}} & {a_{3}} & {a_{4}} & {a_{5}} \\ {3} & {3 \cdot(-2)} & {-6 \cdot(-2)} & {12 \cdot(-2)} & {-24 \cdot(-2)} \\& {-6} & {12} & {-24} & {48}\end{array}\)
Answer:
The sequence is \(3,-6,12,-24,48, \dots\)
Write the first five terms of the sequence where the first term is \(7\) and the common ratio is \(r=−3\).
- Answer
-
\(7,-21,63,-189,567\)
Write the first five terms of the sequence where the first term is \(6\) and the common ratio is \(r=−4\).
- Answer
-
\(6,-24,96,-384,1536\)
Find the General Term (\(n\)th Term) of a Geometric Sequence
Just as we found a formula for the general term of a sequence and an arithmetic sequence, we can also find a formula for the general term of a geometric sequence.
Let’s write the first few terms of the sequence where the first term is \(a_{1}\) and the common ratio is \(r\). We will then look for a pattern.
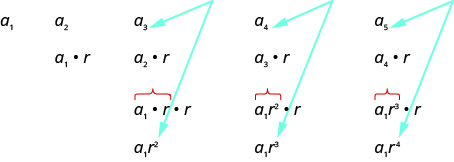
As we look for a pattern in the five terms above, we see that each of the terms starts with \(a_{1}\).
The first term, \(a_{1}\), is not multiplied by any \(r\). In the second term, the \(a_{1}\) is multiplied by \(r\). In the third term, the \(a_{1}\) is multiplied by \(r\) two times (\(r⋅r\) or \(r^{2}\)). In the fourth term, the \(a_{1}\) is multiplied by \(r\) three times (\(r⋅r⋅r\) or \(r^{3}\)) and in the fifth term, the \(a_{1}\) is multiplied by \(r\) four times. In each term, the number of times \(a_{1}\) is multiplied by \(r\) is one less than the number of the term. This leads us to the following
\(a_{n}=a_{1} r^{n-1}\)
The general term of a geometric sequence with first term \(a_{1}\) and the common ratio \(r\) is
\(a_{n}=a_{1} r^{n-1}\)
We will use this formula in the next example to find the fourteenth term of a sequence.
Find the fourteenth term of a sequence where the first term is \(64\) and the common ratio is \(r=\frac{1}{2}\).
Solution:
\(a_{n}=a_{1} r^{n-1}\)
To find the fourteenth term, \(a_{14}\),use the formula with \(a_{1}=64\) and \(r=\frac{1}{2}\).
\(a_{14}=64\left(\frac{1}{2}\right)^{14-1}\)
Substitute in the values.
\(a_{14}=64\left(\frac{1}{2}\right)^{13}\)
Simplify.
\(a_{14}=\frac{1}{128}\)
Find the thirteenth term of a sequence where the first term is \(81\) and the common ratio is \(r=\frac{1}{3}\).
- Answer
-
\(\frac{1}{6,561}\)
Find the twelfth term of a sequence where the first term is \(256\) and the common ratio is \(r=\frac{1}{4}\).
- Answer
-
\(\frac{1}{16,384}\)
Sometimes we do not know the common ratio and we must use the given information to find it before we find the requested term.
Find the twelfth term of the sequence \(3, 6, 12, 24, 48, 96, …\) Find the general term for the sequence.
Solution:
To find the twelfth term, we use the formula, \(a_{n}=a_{1} r^{n-1}\), and so we need to first determine \(a_{1}\) and the common ratio \(r\).
The first term is three.
\(3,6,12,24,48,96, \dots\)
\(a_{1}=3\)
Find the common ratio.
\(\begin{array}{l}{\frac{6}{3} \quad \frac{12}{6} \quad \frac{24}{12} \quad \frac{48}{24} \quad \frac{96}{48}} \\ {2 \:\:\:\quad 2 \quad \:\:2 \quad\:\:\: 2 \:\:\quad \:2} \\ {\text { The common ratio is } r=2}\end{array}\)
To find the twelfth term, \(a_{12}\),use the formula with \(a_{1}=3\) and \(r=2\).
\(a_{n}=a_{1} r^{n-1}\)
Substitute in the values.
\(a_{12}=3 \cdot 2^{12-1}\)
Simplify.
\(a_{12}=3 \cdot 2^{11}\)
\(a_{12}=6,144\)
Find the general term. We use the formula with \(a_{1}=3\) and \(r=2\).
\(a_{n}=a_{1} r^{n-1}\)
\(a_{n}=3(2)^{n-1}\)
Find the ninth term of the sequence \(6, 18, 54, 162, 486, 1,458, … \) Then find the general term for the sequence.
- Answer
-
\(a_{9}=39,366 .\) The general term is \(a_{n}=6(3)^{n-1}\).
Find the eleventh term of the sequence \(7, 14, 28, 56, 112, 224, …\) Then find the general term for the sequence.
- Answer
-
\(a_{11}=7,168 .\) The general term is \(a_{n}=7(2)^{n-1}\).
Find the Sum of the First \(n\) Terms of a Geometric Sequence
We found the sum of both general sequences and arithmetic sequence. We will now do the same for geometric sequences. The sum, \(S_{n}\), of the first \(n\) terms of a geometric sequence is written as \(S_{n}=a_{1}+a_{2}+a_{3}+\ldots+a_{n}\). We can write this sum by starting with the first term, \(a_{1}\), and keep multiplying by \(r\) to get the next term as:
\(S_{n}=a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}\)
Let’s also multiply both sides of the equation by \(r\).
\(r S_{n}=a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n}\)
Next, we subtract these equations. We will see that when we subtract, all but the first term of the top equation and the last term of the bottom equation subtract to zero.
\(\begin{aligned} S_{n}&= a_{1}+a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1} \\ r S_{n} &= a_{1} r+a_{1} r^{2}+a_{1} r^{3}+\ldots+a_{1} r^{n-1}+a_{1} r^{n}\\\hline S_{n}-r S_{n} &= a_{1} -a_{1}r^{n} \end{aligned}\)
We factor both sides.
\(S_{n}(1-r)=a_{1}\left(1-r^{n}\right)\)
To obtain the formula for \(S_{n}\), divide both sides by \((1-r)\).
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
The sum, \(S_{n}\), of the first \(n\) terms of a geometric sequence is
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
where \(a_{1}\) is the first term and \(r\) is the common ratio, and \(r\) is not equal to one.
We apply this formula in the next example where the first few terms of the sequence are given. Notice the sum of a geometric sequence typically gets very large when the common ratio is greater than one.
Find the sum of the first \(20\) terms of the geometric sequence \(7, 14, 28, 56, 112, 224, …\)
Solution:
To find the sum, we will use the formula \(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). We know \(a_{1}=7\), \(r=2\), and \(n=20\),
Knowing \(a_{1}=7, r=2\), and \(n=20\), use the sum formula.
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
Substitute in the values.
\(S_{20}=\frac{7\left(1-2^{20}\right)}{1-2}\)
Simplify.
\(S_{20}=7,340,025\)
Find the sum of the first \(20\) terms of the geometric sequence \(3, 6, 12, 24, 48, 96, …\)
- Answer
-
\(3,145,725\)
Find the sum of the first \(20\) terms of the geometric sequence \(6, 18, 54, 162, 486, 1,458, …\)
- Answer
-
\(10,460,353,200\)
In the next example, we are given the sum in summation notation. While adding all the terms might be possible, most often it is easiest to use the formula to find the sum of the first \(n\) terms.
To use the formula, we need \(r\). We can find it by writing out the first few terms of the sequence and find their ratio. Another option is to realize that in summation notation, a sequence is written in the form \(\sum_{i=1}^{k} a(r)^{i}\), where \(r\) is the common ratio.
Find the sum: \(\sum_{i=1}^{15} 2(3)^{i}\).
Solution:
To find the sum, we will use the formula \(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\), which requires \(a_{1}\) and \(r\). We will write out a few of the terms, so we can get the needed information.
 |
|
| Write out the first few terms. |  |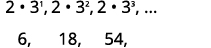
| Identify \(a_{1}\). |  |
| Find the common ratio. |  |
| Knowing \(a_{1}=6\), \(r=3\), and \(n=15\), use the sum formula. |  |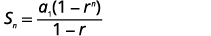
| Substitute in the values. |  |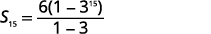
| Simplify. |  |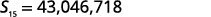
Find the sum: \(\sum_{i=1}^{15} 6(2)^{i}\).
- Answer
-
\(393,204\)
Find the sum: \(\sum_{i=1}^{10} 5(2)^{i}\).
- Answer
-
\(10,230\)
Find the Sum of an Infinite Geometric Series
If we take a geometric sequence and add the terms, we have a sum that is called a geometric series. An infinite geometric series is an infinite sum whose first term is \(a_{1}\) and common ratio is \(r\) and is written
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
An infinite geometric series is an infinite sum whose first term is \(a_{1}\) and common ratio is \(r\) and is written
\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\dots\)
We know how to find the sum of the first \(n\) terms of a geometric series using the formula, \(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\). But how do we find the sum of an infinite sum?
Let’s look at the infinite geometric series \(3+6+12+24+48+96+….\). Each term gets larger and larger so it makes sense that the sum of the infinite number of terms gets larger. Let’s look at a few partial sums for this series. We see \(a_{1}=3\) and \(r=2\)
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{3\left(1-2^{10}\right)}{1-2}} & {S_{30}=\frac{3\left(1-2^{30}\right)}{1-2}} & {S_{50}=\frac{3\left(1-2^{50}\right)}{1-2}} \\ {S_{10}=3,069} & {S_{30}=3,221,225,469} & {S_{50}\approx 3.38 \times 10^{15}}\end{array}\)
As \(n\) gets larger and larger, the sum gets larger and larger. This is true when \(|r|≥1\) and we call the series divergent. We cannot find a sum of an infinite geometric series when \(|r|≥1\).
Let’s look at an infinite geometric series whose common ratio is a fraction less than one,
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\ldots\). Here the terms get smaller and smaller as \(n\) gets larger. Let’s look at a few finite sums for this series. We see \(a_{1}=\frac{1}{2}\) and \(r=\frac{1}{2}\).
\(\begin{array}{lll}{S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}} & {S_{n}=\frac{a_{1}(1-r^{n})}{1-r}}\\ {S_{10}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{10}\right)}{1-\frac{1}{2}}} & {S_{20}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{20}\right)}{1-\frac{1}{2}}} & {S_{30}=\frac{\frac{1}{2}\left(1-\frac{1}{2}^{30}\right)}{1-\frac{1}{2}}} \\ {S_{10}\approx 0.9990234375} & {S_{20}\approx 0.9999990463} & {S_{30}\approx 0.9999999991}\end{array}\)
Notice the sum gets larger and larger but also gets closer and closer to one. When \(|r|<1\), the expression \(r^{n}\) gets smaller and smaller. In this case, we call the series convergent. As \(n\) approaches infinity, (gets infinitely large), \(r^{n}\) gets closer and closer to zero. In our sum formula, we can replace the \(r^{n}\) with zero and then we get a formula for the sum, \(S\), for an infinite geometric series when \(|r|<1\).
\(\begin{aligned} S_{n} &=\frac{a_{1}\left(1-r^{n}\right)}{1-r} \\ S &=\frac{a_{1}(1-0)}{1-r} \\ S &=\frac{a_{1}}{1-r} \end{aligned}\)
This formula gives us the sum of the infinite geometric sequence. Notice the \(S\) does not have the subscript \(n\) as in \(S_{n}\) as we are not adding a finite number of terms.
For an infinite geometric series whose first term is \(a_{1}\) and common ratio \(r\),
If \(|r|<1\),the sum is
\(S=\frac{a_{1}}{1-r}\)
If \(|r|≥1\),the infinite geometric series does not have a sum. We say the series diverges.
Find the sum of the infinite geometric series \(54+18+6+2+\frac{2}{3}+\frac{2}{9}+\ldots\)
Solution:
To find the sum, we first have to verify that the common ratio \(|r|<1\) and then we can use the sum formula \(S=\frac{a_{1}}{1-r}\).
Find the common ratio.
\(\begin{array}{ll}{r=\frac{18}{54}} & {r=\frac{6}{18} \dots} \\ {r=\frac{1}{3}} & {r=\frac{1}{3} \quad|r|<1}\end{array}\)
Identify \(a_{1}\).
\(a_{1}=54\)
Knowing \(a_{1}=54, r=\frac{1}{3}\), use the sum formula.
\(S=\frac{a_{1}}{1-r}\)
Substitute in the values.
\(S=\frac{54}{1-\frac{1}{3}}\)
Simplify.
\(S=81\)
Answer:
\(S=80\)
Find the sum of the infinite geometric series \(48+24+12+6+3+\frac{3}{2}+\dots\)
- Answer
-
\(96\)
Find the sum of the infinite geometric series \(64+16+4+1+\frac{1}{4}+\frac{1}{16}+\dots\)
- Answer
-
\(\frac{256}{3}\)
An interesting use of infinite geometric series is to write a repeating decimal as a fraction.
Write the repeating decimal \(0.5\) as a fraction.
Solution:
Rewrite the \(0.5\) showing the repeating five. Use place value to rewrite this as a sum. This is an infinite geometric series.
0.5555555555555\(\ldots\)
\(0.5+0.05+0.005+0.0005+\dots\)
Find the common ratio.
\(\begin{array}{ll}{r=\frac{0.05}{0.5}} & {r=\frac{0.005}{0.05} \dots} \\ {r=0.1} & {r=0.1 \quad|r|<1}\end{array}\)
Identify \(a_{1}\)
\(a_{1}=0.5\)
Knowing \(a_{1}=0.5 ,r=0.1\), use the sum formula.
\(S=\frac{a_{1}}{1-r}\)
Substitute in the values.
\(S=\frac{0.5}{1-0.1}\)
Simplify.
\(S=\frac{0.5}{0.9}\)
Multiply the numerator and denominator by \(10\).
\(S=\frac{5}{9}\)
We are asked to find the fraction form.
\(0.5 = \frac{5}{9}\)
Write the repeating decimal \(0.4\) as a fraction.
- Answer
-
\(\frac{4}{9}\)
Write the repeating decimal \(0.8\) as a fraction.
- Answer
-
\(\frac{8}{9}\)
Apply Geometric Sequences and Series in the Real World
One application of geometric sequences has to do with consumer spending. If a tax rebate is given to each household, the effect on the economy is many times the amount of the individual rebate.
The government has decided to give a $\(1,000\) tax rebate to each household in order to stimulate the economy. The government statistics say that each household will spend \(80\)% of the rebate in goods and services. The businesses and individuals who benefited from that \(80\)% will then spend \(80\)% of what they received and so on. The result is called the multiplier effect. What is the total effect of the rebate on the economy?
Solution:
Every time money goes into the economy, \(80\)% of it is spent and is then in the economy to be spent. Again, \(80\)% of this money is spent in the economy again. This situation continues and so leads us to an infinite geometric series.
\(1000+1000(0.8)+1000(0.8)^{2}+\ldots\)
Here the first term is \(1,000, a_{1}=1000\). The common ratio is \(0.8, r=0.8\). We can evaluate this sum since \(0.8<1\). We use the formula for the sum on an infinite geometric series.
\(S=\frac{a_{1}}{1-r}\)
Substitute in the values, \(a_{1}=1,000\) and \(r=0.8\).
\(S=\frac{1,000}{1-0.8}\)
Evaluate.
\(S=5,000\)
Answer:
The total effect of the $\(1,000\) received by each household will be a $\(5,000\) growth in the economy.
What is the total effect on the economy of a government tax rebate of $\(1,000\) to each household in order to stimulate the economy if each household will spend \(90\)% of the rebate in goods and services?
- Answer
-
$\(10,000\)
What is the total effect on the economy of a government tax rebate of $\(500\) to each household in order to stimulate the economy if each household will spend \(85\)% of the rebate in goods and services?
- Answer
-
$\(3,333.33\)
We have looked at a compound interest formula where a principal, \(P\), is invested at an interest rate, \(r\), for \(t\) years. The new balance, \(A\), is \(A=P\left(1+\frac{r}{n}\right)^{n t}\) when interest is compounded \(n\) times a year. This formula applies when a lump sum was invested upfront and tells us the value after a certain time period.
An annuity is an investment that is a sequence of equal periodic deposits. We will be looking at annuities that pay the interest at the time of the deposits. As we develop the formula for the value of an annuity, we are going to let \(n=1\). That means there is one deposit per year.
\(\begin{aligned} &A =P\left(1+\frac{r}{n}\right)^{n t} \\ \text { Let } n=1 .\quad & A=P\left(1+\frac{r}{1}\right)^{1 t} \\ \text { Simplify. }\quad & A=P(1+r)^{t} \end{aligned}\)
Suppose \(P\) dollars is invested at the end of each year. One year later that deposit is worth \(P(1+r)^{1}\) dollars, and another year later it is worth \(P(1+r)^{2}\) dollars. After \(t\) years, it will be worth \(P(1+r)^{t}\) dollars.
| End of year \(1\) | End of year \(2\) | End of year \(3\) | |
|---|---|---|---|
| First Deposit \(P\) @ end of year \(1\) | \(P\) | Amount \(1\) year later \(P(1+r)^{1}\) | Amount \(2\) years later \(P(1+r)^{2}\) |
| \(2\)nd Deposit \(P\) @ end of year \(2\) | \(P\) | Amount \(1\) year later \(P(1+r)^{1}\) | |
| \(3\)rd Deposit \(P\) @ end of year \(3\) | \(P\) |
After three years, the value of the annuity is
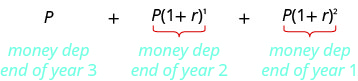
This a sum of the terms of a geometric sequence where the first term is \(P\) and the common ratio is \(1+r\). We substitute these values into the sum formula. Be careful, we have two different uses of \(r\). The \(r\) in the sum formula is the common ratio of the sequence. In this case, that is \(1+r\) where \(r\) is the interest rate.
\(\begin{aligned} &S_{t} =\frac{a_{1}\left(1-r^{t}\right)}{1-r} \\ \text { Substitute in the values. }\quad & S_{t}=\frac{P\left(1-(1+r)^{t}\right)}{1-(1+r)} \\ \text { Simplify. }\quad & S_{t} =\frac{P\left(1-(1+r)^{t}\right)}{-r} \\ &S_{t} =\frac{P\left((1+r)^{t}-1\right)}{r} \end{aligned}\)
Remember our premise was that one deposit was made at the end of each year.
We can adapt this formula for \(n\) deposits made per year and the interest is compounded \(n\) times a year.
For a principal, \(P\), invested at the end of a compounding period, with an interest rate, \(r\), which is compounded \(n\) times a year, the new balance, \(A\), after \(t\) years, is
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
New parents decide to invest $\(100\) per month in an annuity for their baby daughter. The account will pay \(5\)% interest per year which is compounded monthly. How much will be in the child’s account at her eighteenth birthday?
Solution:
To find the Annuity formula, \(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\), we need to identify \(P, r, n\), and \(t\).
Identify \(P\), the amount invested each month.
\(P=100\)
Identify \(r\), the annual interest rate, in decimal form.
\(r=0.05\)
Identify \(n\), the number of times the deposit will be made and the interest compounded each year.
\(n=12\)
Identify \(t\), the number of years.
\(t=18\)
Knowing \(P=100, r=0.05, n=12\) and \(t=18\), use the sum formula.
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Substitute in the values.
\(A_{t}=\frac{100\left(\left(1+\frac{0.05}{12}\right)^{12.18}-1\right)}{\frac{0.05}{12}}\)
Use the calculator to evaluate. Be sure to use parentheses as needed.
\(A_{t}=34.920 .20\)
Answer:
The child will have $\(34,920.20\)
New grandparents decide to invest $\(200\) per month in an annuity for their grandson. The account will pay \(5\)% interest per year which is compounded monthly. How much will be in the child’s account at his twenty-first birthday?
- Answer
-
$\(88,868.36\)
Arturo just got his first full-time job after graduating from college at age \(27\). He decided to invest $\(200\) per month in an IRA (an annuity). The interest on the annuity is \(8\)%, which is compounded monthly. How much will be in the Arturo’s account when he retires at his sixty-seventh birthday?
- Answer
-
$\(698,201.57\)
Access these online resources for additional instruction and practice with sequences.
Key Concepts
- General Term (\(n\)th term) of a Geometric Sequence: The general term of a geometric sequence with first term \(a_{1}\) and the common ratio \(r\) is
\(a_{n}=a_{1} r^{n-1}\)
- Sum of the First \(n\) Terms of a Geometric Series: The sum, \(S_{n}\), of the \(n\) terms of a geometric sequence is
\(S_{n}=\frac{a_{1}\left(1-r^{n}\right)}{1-r}\)
where \(a_{1}\) is the first term and \(r\) is the common ratio.Infinite Geometric Series: An infinite geometric series is an infinite sum whose first term is \(a_{1}\) and common ratio is \(r\) and is written\(a_{1}+a_{1} r+a_{1} r^{2}+\ldots+a_{1} r^{n-1}+\ldots\)
- Sum of an Infinite Geometric Series: For an infinite geometric series whose first term is \(a_{1}\) and common ratio \(r\),
If \(|r|<1\),the sum is
\(S=\frac{a_{1}}{1-r}\)
We say the series converges.
If \(|r|≥1\), the infinite geometric series does not have a sum. We say the series diverges.
- Value of an Annuity with Interest Compounded \(n\) Times a Year: For a principal, \(P\), invested at the end of a compounding period, with an interest rate, \(r\), which is compounded \(n\) times a year, the new balance, \(A\), after \(t\) years, is
\(A_{t}=\frac{P\left(\left(1+\frac{r}{n}\right)^{n t}-1\right)}{\frac{r}{n}}\)
Glossary
- annuity
- An annuity is an investment that is a sequence of equal periodic deposits.
- common ratio
- The ratio between consecutive terms in a geometric sequence, \(\frac{a_{n}}{a_{n-1}}\), is \(r\), the common ratio, where \(r\) greater than or equal to two.
- geometric sequence
- A geometric sequence is a sequence where the ratio between consecutive terms is always the same
- infinite geometric series
- An infinite geometric series is an infinite sum infinite geometric sequence.