3.9: Bounded Sets. Diameters
- Page ID
- 20136
I. Geometrically, the diameter of a closed globe in \(E^{n}\) could be defined as the maximum distance between two of its points. In an open globe in \(E^{n},\) there is no "maximum" distance (why?), but we still may consider the supremum of all distances inside the globe. Moreover, this makes sense in any set \(A \subseteq(S, \rho) .\) Thus we accept it as a general definition, for any such set.
The diameter of a set \(A \neq \emptyset\) in a metric space \((S, \rho),\) denoted \(d A,\) is the supremum (in \(E^{*}\)) of all distances \(\rho(x, y),\) with \(x, y \in A ;^{1}\) in symbols,
\[d A=\sup _{x, y \in A} \rho(x, y).\]
If \(A=\emptyset,\) we put \(d A=0 .\) If \(d A<+\infty, A\) is said to be bounded \((\) in \((S, \rho) ) .\)
Equivalently, we could define a bounded set as in the statement of the following theorem.
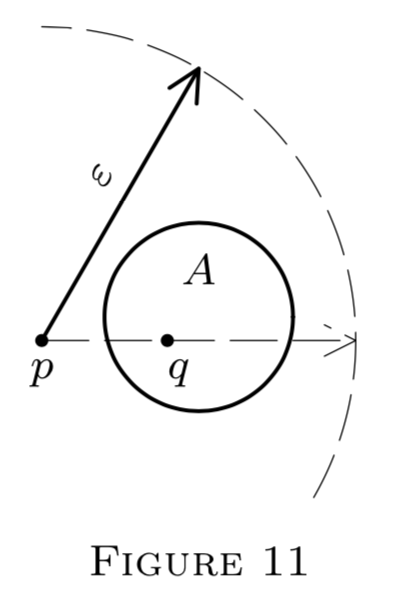
\(A\) set \(A \subseteq(S, \rho)\) is bounded iff \(A\) is contained in some globe. If so, the center p of this globe can be chosen at will.
- Proof
-
If \(A=\emptyset,\) all is trivial.
Thus let \(A \neq \emptyset ;\) let \(q \in A,\) and choose any \(p \in S .\) Now if \(A\) is bounded, then \(d A<+\infty,\) so we can choose a real \(\varepsilon>\) \(\rho(p, q)+d A\) as a suitable radius for a globe \(G_{p}(\varepsilon) \supseteq A(\) see Figure 11 for motivation\().\) Now if \(x \in A,\) then by the definition of \(d A\) \(\rho(q, x) \leq d A ;\) so by the triangle law,
\(\begin{aligned} \rho(p, x) & \leq \rho(p, q)+\rho(q, x) \\ & \leq \rho(p, q)+d A<\varepsilon; \end{aligned}\)
i.e., \(x \in G_{p}(\varepsilon) .\) Thus \((\forall x \in A) x \in G_{p}(\varepsilon)\) as required.
Conversely, if \(A \subseteq G_{p}(\varepsilon),\) then any \(x, y \in A\) are also in \(G_{p}(\varepsilon) ;\) so \(\rho(x, p)<\varepsilon\) and \(\rho(p, y)<\varepsilon,\) whence
\[\rho(x, y) \leq \rho(x, p)+\rho(p, y)<\varepsilon+\varepsilon=2 \varepsilon.\]
Thus 2\(\varepsilon\) is an upper bound of all \(\rho(x, y)\) with \(x, y \in A .\) Therefore,
\[d A=\sup \rho(x, y) \leq 2 \varepsilon<+\infty;\]
i.e., \(A\) is bounded, and all is proved. \(\square\)
As a special case we obtain the following.
\(A\) set \(A \subseteq E^{n}\) is bounded iff there is a real \(K>0\) such that
\[(\forall \overline{x} \in A) \quad|\overline{x}|<K\]
(*similarly in \(C^{n}\) and other normed spaces).
- Proof
-
By Theorem \(1(\) choosing \(\overline{0}\) for \(p), A\) is bounded iff \(A\) is contained in some globe \(G_{\overline{0}}(\varepsilon)\) about \(\overline{0} .\) That is,
\[(\forall \overline{x} \in A) \quad \overline{x} \in G_{\overline{0}}(\varepsilon)\text{ or } \rho(\overline{x}, \overline{0})=|\overline{x}|<\varepsilon.\]
Thus \(\varepsilon\) is the required \(K\).(*The proof for normed spaces is the same.) \(\square\)
Note 1. In \(E^{1},\) this means that
\[(\forall x \in A) \quad-K<x<K;\]
i.e., \(A\) is bounded by \(-K\) and \(K .\) This agrees with our former definition, given in Chapter 2, §§8-9.
Caution: Upper and lower bounds are not defined in \((S, \rho),\) in general.
(1) \(\emptyset\) is bounded, with \(d \emptyset=0,\) by definition.
(2) Let \(A=[\overline{a}, \overline{b}]\) in \(E^{n},\) with \(d=\rho(\overline{a}, \overline{b})\) its diagonal. By Corollary 1 in §7 \(d\) is the largest distance in \(A .\) In nonclosed intervals, we still have
\[d=\sup _{x, y \in A} \rho(x, y)=d A<+\infty\text{ (see Problem 10 (ii)).}\]
Thus all intervals in \(E^{n}\) are bounded.
(3) Each globe \(G_{p}(\varepsilon)\) in \((S, \rho)\) is bounded, with \(d G_{p}(\varepsilon) \leq 2 \varepsilon<+\infty,\) as was shown in the proof of Theorem \(1 .\) See, however, Problems 5 and 6 below.
(4) All of \(E^{n}\) is not bounded, under the standard metric, for if \(E^{n}\) had a finite diameter \(d,\) no distance in \(E^{n}\) would exceed \(d ;\) but \(\rho\left(-d \overline{e}_{1}, d \overline{e}_{1}\right)=2 d\), a contradiction!
(5) On the other hand, under the discrete metric §11, Example (3)), any set (even the entire space) is contained in \(G_{p}(3)\) and hence bounded. The same applies to the metric \(\rho^{\prime}\) defined for \(E^{*}\) in Problem 5 of §§11, since distances under that metric never exceed \(2,\) and so \(E^{*} \subseteq G_{p}(3)\) for any choice of \(p\).
Note 2. This shows that boundedness depends on the metric \(\rho .\) A set may be bounded under one metric and not bounded under another. A metric \(\rho\) is said to be bounded iff all sets are bounded under \(\rho\) (as in Example (5)).
Problem 9 of §11 shows that any metric \(\rho\) can be transformed into a bounded one, even preserving all sufficiently small globes; in part (i) of the problem, even the radii remain the same if they are \(\leq 1\).
Note 3. An idea similar to that of diameter is often used to define distances between sets. If \(A \neq \emptyset\) and \(B \neq \emptyset\) in \((S, \rho),\) we define \(\rho(A, B)\) to be the infimum of all distances \(\rho(x, y),\) with \(x \in A\) and \(y \in B .\) In particular, if \(B=\{p\}\) (a singleton\(),\) we write \(\rho(A, p)\) for \(\rho(A, B).\) Thus
\[\rho(A, p)=\inf _{x \in A} \rho(x, p).\]
II. The definition of boundedness extends, in a natural manner, to sequences and functions. We briefly write \(\left\{x_{m}\right\} \subseteq(S, \rho)\) for a sequence of points in \((S, \rho)\), and \(f : A \rightarrow(S, \rho)\) for a mapping of an arbitrary set \(A\) into the space \(S .\) Instead of "infinite sequence with general term \(x_{m},\)" we say "the sequence \(x_{m}\)."
A sequence \(\left\{x_{m}\right\} \subseteq(S, \rho)\) is said to be bounded iff its range is bounded in \((S, \rho),\) i.e., iff all its terms \(x_{m}\) are contained in some globe in \((S, \rho).\)
In \(E^{n},\) this means (by Theorem 2\()\) that
\[(\forall m) \quad\left|x_{m}\right|<K\]
for some fixed \(K \in E^{1}.\)
A function \(f : A \rightarrow(S, \rho)\) is said to be bounded on a set \(B \subseteq A\) iff the image set \(f[B]\) is bounded in \((S, \rho) ;\) i.e. iff all function values \(f(x),\) with \(x \in B,\) are in some globe in \((S, \rho)\).
In \(E^{n},\) this means that
\[(\forall x \in B) \quad|f(x)|<K\]
for some fixed \(K \in E^{1}.\)
If \(B=A,\) we simply say that \(f\) is bounded.
Note 4. If \(S=E^{1}\) or \(S=E^{*},\) we may also speak of upper and lower bounds. It is customary to call sup \(f[B]\) also the supremum of \(f\) on \(B\) and denote it by symbols like
\[\sup _{x \in B} f(x)\text{ or } \sup \{f(x) | x \in B\}.\]
In the case of sequences, we often write sup \(_{m} x_{m}\) or sup \(x_{m}\) instead; similarly for infima, maxima, and minima.
(a) The sequence
\[x_{m}=\frac{1}{m} \quad\text{ in } E^{1}\]
is bounded since all terms \(x_{m}\) are in the interval \((0,2)=G_{1}(1) .\) We have inf \(x_{m}=0\) and \(\sup x_{m}=\max x_{m}=1.\)
(b) The sequence
\[x_{m}=m \quad\text{ in } E^{1}\]
is bounded below (by 1\()\) but not above. We have inf \(x_{m}=\min x_{m}=1\) and \(\sup x_{m}=+\infty\) (in \(E^{*})\).
(c) Define \(f : E^{1} \rightarrow E^{1}\) by
\[f(x)=2 x.\]
This map is bounded on each finite interval \(B=(a, b)\) since \(f[B]=\) \((2 a, 2 b)\) is itself an interval and hence bounded. However, \(f\) is not bounded on all of \(E^{1}\) since \(f\left[E^{1}\right]=E^{1}\) is not a bounded set.
(d) Under a bounded metric \(\rho,\) all functions \(f : A \rightarrow(S, \rho)\) are bounded.
(e) The so-called identity map on \(S, f : S \rightarrow(S, \rho),\) is defined by
\[f(x)=x.\]
Clearly, \(f\) carries each set \(B \subseteq S\) onto itself; i.e., \(f[B]=B .\) Thus \(f\) is bounded on \(B\) iff \(B\) is itself a bounded set in \((S, \rho).\)
(f) Define \(f : E^{1} \rightarrow E^{1}\) by
\[f(x)=\sin x.\]
Then \(f\left[E^{1}\right]=[-1,1]\) is a bounded set in the range space \(E^{1} .\) Thus \(f\) is bounded on \(E^{1}\) (briefly, bounded).


