5.7: The Total Variation (Length) of a Function f - E1 → E
- Page ID
- 21242
This page is a draft and is under active development.
The question that we shall consider now is how to define reasonably (and precisely) the notion of the length of a curve (Chapter 4, §10) described by a function \(f : E^{1} \rightarrow E\) over an interval \(I=[a, b],\) i.e., \(f[I]\).
We proceed as follows (see Figure 24).
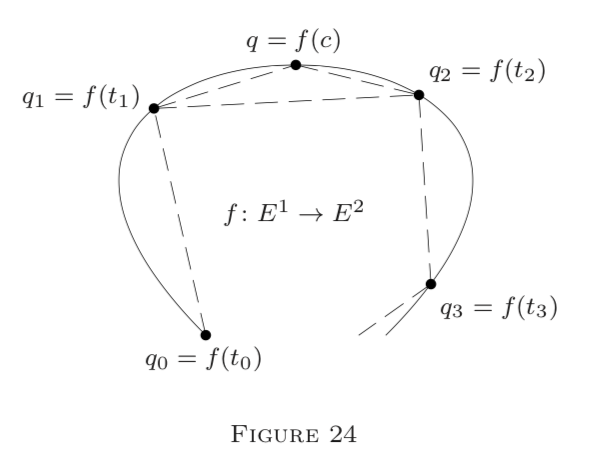
Subdivide \([a, b]\) by a finite set of points \(P=\left\{t_{0}, t_{1}, \ldots, t_{m}\right\},\) with
\[a=t_{0} \leq t_{1} \leq \cdots \leq t_{m}=b;\]
\(P\) is called a partition of \([a, b].\) Let
\[q_{i}=f\left(t_{i}\right), \quad i=1,2, \ldots, m,\]
and, for \(i=1,2, \ldots, m\),
\[\begin{aligned} \Delta_{i} f &=q_{i}-q_{i-1} \\ &=f\left(t_{i}\right)-f\left(t_{i-1}\right). \end{aligned}\]
We also define
\[S(f, P)=\sum_{i=1}^{m}\left|\Delta_{i} f\right|=\sum_{i=1}^{m}\left|q_{i}-q_{i-1}\right|.\]
Geometrically, \(\left|\Delta_{i} f\right|=\left|q_{i}-q_{i-1}\right|\) is the length of the line segment \(L\left[q_{i-1}, q_{i}\right]\) in \(E,\) and \(S(f, P)\) is the sum of such lengths, i.e., the length of the polygon
\[W=\bigcup_{i=1}^{m} L\left[q_{i-1}, q_{i}\right]\]
inscribed into \(f[I];\) we denote it by
\[\ell W=S(f, P).\]
Now suppose we add a new partition point \(c,\) with
\[t_{i-1} \leq c \leq t_{i}.\]
Then we obtain a new partition
\[P_{c}=\left\{t_{0}, \ldots, t_{i-1}, c, t_{i}, \ldots, t_{m}\right\},\]
called a refinement of \(P,\) and a new inscribed polygon \(W_{c}\) in which \(L\left[q_{i-1}, q_{i}\right]\) is replaced by two segments, \(L\left[q_{i-1}, q\right]\) and \(L\left[q, q_{i}\right],\) where \(q=f(c);\) see Figure 24. Accordingly, the term \(\left|\Delta_{i} f\right|=\left|q_{i}-q_{i-1}\right|\) in \(S(f, P)\) is replaced by
\[\left|q_{i}-q\right|+\left|q-q_{i-1}\right| \geq\left|q_{i}-q_{i-1}\right| \quad \text { (triangle law)}.\]
It follows that
\[S(f, P) \leq S\left(f, P_{c}\right) ; \text { i.e., } \ell W \leq \ell W_{c}.\]
Hence we obtain the following result.
The sum \(S(f, P)=\ell W\) cannot decrease when \(P\) is refined.
Thus when new partition points are added, \(S(f, P)\) grows in general; i.e., it approaches some supremum value (finite or not). Roughly speaking, the inscribed polygon \(W\) gets "closer" to the curve. It is natural to define the desired length of the curve to be the \(l u b\) of all lengths \(\ell W,\) i.e., of all sums \(S(f, P)\) resulting from the various partitions \(P\). This supremum is also called the total variation of \(f\) over \([a, b],\) denoted \(V_{f}[a, b].\)
Given any function \(f : E^{1} \rightarrow E,\) and \(I=[a, b] \subset E^{1},\) we set
\[V_{f}[I]=V_{f}[a, b]=\sup _{P} S(f, P)=\sup _{P} \sum_{i=1}^{m}\left|f\left(t_{i}\right)-f\left(t_{i-1}\right)\right| \geq 0 \text { in } E^{*},\]
where the supremum is over all partitions \(P=\left\{t_{0}, \ldots, t_{m}\right\}\) of \(I.\) We call \(V_{f}[I]\) the total variation, or length, of \(f\) on \(I.\) Briefly, we denote it by \(V_{f}\).
Note 1. If \(f\) is continuous on \([a, b],\) the image set \(A=f[I]\) is an arc (Chapter 4, §10). It is customary to call \(V_{f}[I]\) the length of that arc, denoted \(\ell_{f} A\) or briefly \(\ell A.\) Note, however, that there may well be another function \(g,\) continuous on an interval \(J,\) such that \(g[J]=A\) but \(V_{f}[I] \neq V_{g}[J],\) and so \(\ell_{f} A \neq \ell_{g} A.\) Thus it is safer to say "the length of \(A\) as described by \(f\) on I." Only for simple arcs (where \(f\) is one to one), is "\(\ell A\)" unambiguous. (See Problems 6-8.)
In the propositions below, \(f\) is an arbitrary function, \(f : E^{1} \rightarrow E\).
If \(a \leq c \leq b,\) then
\[V_{f}[a, b]=V_{f}[a, c]+V_{f}[c, b];\]
i.e., the length of the whole equals the sum of the lengths of the parts.
- Proof
-
Take any partition \(P=\left\{t_{0}, \ldots, t_{m}\right\}\) of \([a, b].\) If \(c \notin P,\) refine \(P\) to
\[P_{c}=\left\{t_{0}, \ldots, t_{i}, c, t_{i}, \ldots, t_{m}\right\}.\]
Then by Corollary 1, \(S(f, P) \leq S\left(f, P_{c}\right)\).
Now \(P_{c}\) splits into partitions of \([a, c]\) and \([c, b],\) namely,
\[P^{\prime}=\left\{t_{0}, \ldots, t_{i-1}, c\right\} \text { and } P^{\prime \prime}=\left\{c, t_{i}, \ldots, t_{m}\right\},\]
so that
\[S\left(f, P^{\prime}\right)+S\left(f, P^{\prime \prime}\right)=S\left(f, P_{c}\right) . \text { (Verify!)}\]
Hence \(\left(\text {as } V_{f} \text { is the } l u b \text { of the corresponding sums}\right)\),
\[V_{f}[a, c]+V_{f}[c, d] \geq S\left(f, P_{c}\right) \geq S(f, P).\]
As \(P\) is an arbitrary partition of \([a, b],\) we also have
\[V_{f}[a, c]+V_{f}[c, b] \geq \sup S(f, P)=V_{f}[a, b].\]
Thus it remains to show that, conversely,
\[V_{f}[a, b] \geq V_{f}[a, c]+V_{f}[c, b].\]
The latter is trivial if \(V_{f}[a, b]=+\infty.\) Thus assume \(V_{f}[a, b]=K<+\infty.\) Let \(P^{\prime}\) and \(P^{\prime \prime}\) be any partitions of \([a, c]\) and \([c, b],\) respectively. Then \(P^{*}=P^{\prime} \cup P^{\prime \prime}\) is a partition of \([a, b],\) and
\[S\left(f, P^{\prime}\right)+S\left(f, P^{\prime \prime}\right)=S\left(f, P^{*}\right) \leq V_{f}[a, b]=K,\]
whence
\[S\left(f, P^{\prime}\right) \leq K-S\left(f, P^{\prime \prime}\right).\]
Keeping \(P^{\prime \prime}\) fixed and varying \(P^{\prime},\) we see that \(K-S\left(f, P^{\prime \prime}\right)\) is an upper bound of all \(S\left(f, P^{\prime}\right)\) over \([a, c].\) Hence
\[V_{f}[a, c] \leq K-S\left(f, P^{\prime \prime}\right)\]
or
\[S\left(f, P^{\prime \prime}\right) \leq K-V_{f}[a, c].\]
Similarly, varying \(P^{\prime \prime},\) we now obtain
\[V_{f}[c, b] \leq K-V_{f}[a, c]\]
or
\[V_{f}[a, c]+V_{f}[c, b] \leq K=V_{f}[a, b],\]
as required. Thus all is proved. \(\quad \square\)
If \(a \leq c \leq d \leq b,\) then
\[V_{f}[c, d] \leq V_{f}[a, b].\]
- Proof
-
By Theorem 1,
\[V_{f}[a, b]=V_{f}[a, c]+V_{f}[c, d]+V_{f}[d, b] \geq V_{f}[c, d] . \quad \square\]
If \(V_{f}[a, b]<+\infty,\) we say that \(f\) is of bounded variation on \(I=[a, b],\) and that the set \(f[I]\) is rectifiable (by \(f\) on \(I)\).
For each \(t \in[a, b]\),
\[|f(t)-f(a)| \leq V_{f}[a, b].\]
Hence if \(f\) is of bounded variation on \([a, b],\) it is bounded on \([a, b]\).
- Proof
-
If \(t \in[a, b],\) let \(P=\{a, t, b\},\) so
\[|f(t)-f(a)| \leq|f(t)-f(a)|+|f(b)-f(t)|=S(f, P) \leq V_{f}[a, b],\]
proving our first assertion. Hence
\[(\forall t \in[a, b]) \quad|f(t)| \leq|f(t)-f(a)|+|f(a)| \leq V_{f}[a, b]+|f(a)|.\]
This proves the second assertion. \(\quad \square\)
Note 2. Neither boundedness, nor continuity, nor differentiability of \(f\) on \([a, b]\) implies \(V_{f}[a, b]<+\infty,\) but boundedness of \(f^{\prime}\) does. (See Problems 1 and 3.)
A function \(f\) is finite and constant on \([a, b]\) iff \(V_{f}[a, b]=0\).
The proof is left to the reader. (Use Corollary 3 and the definitions.
Let \(f, g, h\) be real or complex (or let \(f\) and \(g\) be vector valued and \(h\) scalar valued). Then on any interval \(I=[a, b],\) we have
(i) \(V_{|f|} \leq V_{f}\);
(ii) \(V_{f \pm g} \leq V_{f}+V_{g} ;\) and
(iii) \(V_{h f} \leq s V_{f}+r V_{h},\) with \(r=\sup _{t \in I}|f(t)|\) and \(s=\sup _{t \in I}|h(t)|\).
Hence if \(f, g,\) and \(h\) are of bounded variation on \(I,\) so are \(f \pm g, h f,\) and \(|f|\).
- Proof
-
We first prove (iii).
Take any partition \(P=\left\{t_{0}, \ldots, t_{m}\right\}\) of \(I.\) Then
\[\begin{aligned}\left|\Delta_{i} h f\right| &=\left|h\left(t_{i}\right) f\left(t_{i}\right)-h\left(t_{i-1}\right) f\left(t_{i-1}\right)\right| \\ & \leq\left|h\left(t_{i}\right) f\left(t_{i}\right)-h\left(t_{i-1}\right) f\left(t_{i}\right)\right|+\left|h\left(t_{i-1}\right) f\left(t_{i}\right)-h\left(t_{i-1}\right) f\left(t_{i-1}\right)\right| \\ &
=\left|f\left(t_{i}\right)\left\|\Delta_{i} h|+| h\left(t_{i-1}\right)\right\| \Delta_{i} f\right|
\\ & \leq r\left|\Delta_{i} h\right|+s\left|\Delta_{i} f\right|. \end{aligned}\]Adding these inequalities, we obtain
\[S(h f, P) \leq r \cdot S(h, P)+s \cdot S(f, P) \leq r V_{h}+s V_{f}.\]
As this holds for all sums \(S(h f, P),\) it holds for their supremum, so
\[V_{h f}=\sup S(h f, P) \leq r V_{h}+s V_{f},\]
as claimed.
Similarly, (i) follows from
\[| | f\left(t_{i}\right)|-| f\left(t_{i-1}\right)| | \leq\left|f\left(t_{i}\right)-f\left(t_{i-1}\right)\right|.\]
The analogous proof of (ii) is left to the reader.
Finally, (i)-(iii) imply that \(V_{f}, V_{f \pm g}\), and \(V_{h f}\) are finite if \(V_{f}, V_{g},\) and \(V_{h}\) are. This proves our last assertion. \(\quad \square\)
Note 3. Also \(f / h\) is of bounded variation on \(I\) if \(f\) and \(h\) are, provided \(h\) is bounded away from 0 on \(I ;\) i.e.,
\[(\exists \varepsilon>0) \quad|h| \geq \varepsilon \text { on } I.\]
(See Problem 5.)
Special theorems apply in case the range space \(E\) is \(E^{1}\) or \(E^{n}\left(^{*} \text { or } C^{n}\right)\).
(i) A real function \(f\) is of bounded variation on \(I=[a, b]\) iff \(f=g-h\) for some nondecreasing real functions \(g\) and \(h\) on \(I.\)
(ii) If \(f\) is real and monotone on \(I,\) it is of bounded variation there.
- Proof
-
We prove (ii) first.
Let \(f \uparrow\) on \(I.\) If \(P=\left\{t_{0}, \ldots, t_{m}\right\},\) then
\[t_{i} \geq t_{i-1} \text { implies } f\left(t_{i}\right) \geq f\left(t_{i-1}\right).\]
Hence \(\Delta_{i} f \geq 0;\) i.e., \(\left|\Delta_{i} f\right|=\Delta_{i} f.\) Thus
\[\begin{aligned} S(f, P) &=\sum_{i=1}^{m}\left|\Delta_{i} f\right|=\sum_{i=1}^{m} \Delta_{i} f=\sum_{i=1}^{m}\left[f\left(t_{i}\right)-f\left(t_{i-1}\right)\right] \\ &=f\left(t_{m}\right)-f\left(t_{0}\right)=f(b)-f(a) \end{aligned}\]
for any \(P.\) (Verify!) This implies that also
\[V_{f}[I]=\sup S(f, P)=f(b)-f(a)<+\infty.\]
Thus (ii) is proved.
Now for (i), let \(f=g-h\) with \(g \uparrow\) and \(h \uparrow\) on \(I\). By (ii), \(g\) and \(h\) are of bounded variation on \(I.\) Hence so is \(f=g-h\) by Theorem 2 (last clause).
Conversely, suppose \(V_{f}[I]<+\infty.\) Then define
\[g(x)=V_{f}[a, x], x \in I, \text { and } h=g-f \text { on } I,\]
so \(f=g-h,\) and it only remains to show that \(g \uparrow\) and \(h \uparrow\).
To prove it, let \(a \leq x \leq y \leq b.\) Then Theorem 1 yields
\[V_{f}[a, y]-V_{f}[a, x]=V_{f}[x, y];\]
i.e.,
\[g(y)-g(x)=V_{f}[x, y] \geq|f(y)-f(x)| \geq 0 \quad \text { (by Corollary 3).}\]
Hence \(g(y) \geq g(x).\) Also, as \(h=g-f,\) we have
\[\begin{aligned} h(y)-h(x) &=g(y)-f(y)-[g(x)-f(x)] \\ &=g(y)-g(x)-[f(y)-f(x)] \\ & \geq 0 \quad \text {by (2).} \end{aligned}\]
Thus \(h(y) \geq h(x).\) We see that \(a \leq x \leq y \leq b\) implies \(g(x) \leq g(y)\) and \(h(x) \leq h(y),\) so \(h \uparrow\) and \(g \uparrow,\) indeed. \(\quad \square\)
(i) A function \(f : E^{1} \rightarrow E^{n}\left(^{*} C^{n}\right)\) is of bounded variation on \(I=[a, b]\) iff all of its components \(\left(f_{1}, f_{2}, \ldots, f_{n}\right)\) are.
(ii) If this is the case, then finite limits \(f\left(p^{+}\right)\) and \(f\left(q^{-}\right)\) exist for every \(p \in[a, b) \text { and } q \in(a, b].\)
- Proof
-
(i) Take any partition \(P=\left\{t_{0}, \ldots, t_{m}\right\}\) of \(I.\) Then
\[\left|f_{k}\left(t_{i}\right)-f_{k}\left(t_{i-1}\right)\right|^{2} \leq \sum_{j=1}^{n}\left|f_{j}\left(t_{i}\right)-f_{j}\left(t_{i-1}\right)\right|^{2}=\left|f\left(t_{i}\right)-f\left(t_{i-1}\right)\right|^{2};\]
i.e., \(\left|\Delta_{i} f_{k}\right| \leq\left|\Delta_{i} f\right|, i=1,2, \ldots,\text{ } m.\) Thus
\[(\forall P) \quad S\left(f_{k}, P\right) \leq S(f, P) \leq V_{f},\]
and \(V_{f_{k}} \leq V_{f}\) follows. Thus
\[V_{f}<+\infty \text { implies } V_{f_{k}}<+\infty, \quad k=1,2, \ldots,\text{ } n.\]
The converse follows by Theorem 2 since \(f=\sum_{k=1}^{n} f_{k} \vec{e}_{k}.\) (Explain!)
(ii) For real monotone functions, \(f\left(p^{+}\right)\) and \(f\left(q^{-}\right)\) exist by Theorem 1 of Chapter 4, §5. This also applies if \(f\) is real and of bounded variation, for by Theorem 3,
\[f=g-h \text { with } g \uparrow \text { and } h \uparrow \text { on } I,\]
and so
\[f\left(p^{+}\right)=g\left(p^{+}\right)-h\left(p^{+}\right) \text { and } f\left(q^{-}\right)=g\left(q^{-}\right)-h\left(q^{-}\right) \text { exist.}\]
The limits are finite since \(f\) is bounded on \(I\) by Corollary 3.
Via components (Theorem 2 of Chapter 4, §3), this also applies to functions \(f : E^{1} \rightarrow E^{n}.\) (Why?) In particular, (ii) applies to complex functions (treat \(C\) as \(E^{2}\) (*and so it extends to functions \(f : E^{1} \rightarrow C^{n}.\) as well). \(\quad \square\)
We also have proved the following corollary.
A complex function \(f : E^{1} \rightarrow C\) is of bounded variation on \([a, b]\) iff its real and imaginary parts are. (See Chapter 4, §3, Note 5).


