1.6: Euler's Formula

Euler’s (pronounced ‘oilers’) formula connects complex exponentials, polar coordinates, and sines and cosines. It turns messy trig identities into tidy rules for exponentials. We will use it a lot. The formula is the following:

\[e^{i\theta} = \cos (\theta) + i \sin (\theta). \label{1.6.1} \]

There are many ways to approach Euler’s formula. Our approach is to simply take Equation \ref{1.6.1} as the definition of complex exponentials. This is legal, but does not show that it’s a good definition. To do that we need to show the \(e^{i \theta}\) obeys all the rules we expect of an exponential. To do that we go systematically through the properties of exponentials and check that they hold for complex exponentials.

\(e^{i \theta}\) behaves like a true exponential

P1

\(e^{i t}\) differentiates as expected:

\[\dfrac{de^{it}}{dt} = ie^{it}.\nonumber \]

Proof

This follows directly from the definition in Equation \ref{1.6.1}:

\[ \begin{align*} \dfrac{de^{it}}{dt} &= \dfrac{d}{dt} (\cos (t) + i \sin (t)) \\[4pt] &= -\sin (t) + i \cos (t) \\[4pt] &= i (\cos (t) + i \sin (t)) \\[4pt] &= ie^{it}. \end{align*} \]

P2

\[e^{i \cdot 0} = 1 . \nonumber \]

Proof

This follows directly from the definition in Equation \ref{1.6.1}:

\(e^{i \cdot 0} = \cos (0) + i \sin (0) = 1\).

P3

The usual rules of exponents hold:

\[e^{ia} e^{ib} = e^{i(a + b)}.\nonumber \]

Proof

This relies on the cosine and sine addition formulas and the definition in Equation \ref{1.6.1}:

\[\begin{align*} e^{ia} \cdot e^{ib} & = (\cos (a) + i \sin (a)) \cdot (\cos (b) + i \sin (b)) \\[4pt] & = \cos (a) \cos (b) - \sin (a) \sin (b) + i (\cos (a) \sin (b) + \sin (a) \cos (b)) \\[4pt] & = \cos (a + b) + i \sin (a + b) = e^{i (a + b)}. \end{align*} \]

P4

The definition of \(e^{i \theta}\) is consistent with the power series for \(e^x\).

Proof

To see this we have to recall the power series for \(e^x\), \(\cos (x)\) and \(\sin (x)\). They are

\[\begin{align*} e^x & = 1 + x + \dfrac{x^2}{2!} + \dfrac{x^3}{3!} + \dfrac{x^4}{4!} + ... \\[4pt] \cos (x) & = 1 - \dfrac{x^2}{2!} + \dfrac{x^4}{4!} - \dfrac{x^6}{6!} + \ldots \\[4pt] \sin (x) & = x - \dfrac{x^3}{3!} + \dfrac{x^5}{5!} + ... \end{align*} \]

Now we can write the power series for \(e^{i \theta}\) and then split it into the power series for sine and cosine:

\[\begin{align*} e^{i \theta} & = \sum_{0}^{\infty} \dfrac{(i\theta)^n}{n!} \\[4pt] & = \sum_{0}^{\infty} (-1)^k \dfrac{\theta ^{2k}}{(2k)!} + i \sum_{0}^{\infty} (-1)^k \dfrac{\theta ^{2k + 1}}{(2k + 1)!} \\[4pt] & = \cos (\theta) + i \sin (\theta). \end{align*} \]

So the Euler formula definition is consistent with the usual power series for \(e^x\).

Properties P1-P4 should convince you that \(e^{i \theta}\) behaves like an exponential.

Complex Exponentials and Polar Form

Now let’s turn to the relation between polar coordinates and complex exponentials.

Suppose \(z = x + iy\) has polar coordinates \(r\) and \(\theta\). That is, we have \(x = r \cos (\theta)\) and \(y = r \sin (\theta)\). Thus, we get the important relationship

\[ \begin{align*} z &= x + iy \\[4pt] &= r \cos (\theta) + i r \sin (\theta) \\[4pt] &= r (\cos (\theta) + i \sin (\theta)) \\[4pt] &= r e^{i \theta}. \end{align*} \]

This is so important you shouldn’t proceed without understanding. We also record it without the intermediate equation.

\[z = x + iy = r e^{i \theta}. \nonumber \]

Because \(r\) and \(\theta\) are the polar coordinates of \((x, y)\) we call \(z = r e^{i \theta}\) the polar form of \(z\).

Let’s now verify that magnitude, argument, conjugate, multiplication and division are easy in polar form.

Magnitude

\(|e^{i \theta}| = 1\).

Proof

\[ \begin{align*} |e^{i \theta}| &= |\cos (\theta) + i \sin (\theta)| \\[4pt] &= \sqrt{\cos ^2 (\theta) + \sin ^2 (\theta)} \\[4pt] &= 1 . \end{align*} \]

In words, this says that \(e^{i \theta}\) is always on the unit circle - this is useful to remember!

Likewise, if \(z = r e^{i \theta}\) then \(|z| = r\). You can calculate this, but it should be clear from the definitions: \(|z|\) is the distance from \(z\) to the origin, which is exactly the same definition as for \(r\).

Argument

If \(z = r e^{i \theta}\) then \(\text{arg} (z) = \theta\).

Proof

This is again the definition: the argument is the polar angle \(\theta\).

Conjugate

\(\overline{(z = r e^{i \theta})} = r e^{-i \theta}\).

Proof

\[ \begin{align*} \overline{(z = r e^{i \theta})} &= \overline{r (\cos (\theta) + i \sin (\theta))} \\[4pt] &= r (\cos (\theta) - i \sin (\theta)) \\[4pt] &= r(\cos (-\theta) + i \sin (-\theta)) \\[4pt] &= r e^{-i \theta}. \end{align*} \]

In words: complex conjugation changes the sign of the argument.

Multiplication

If \(z_1 = r_1 e^{i \theta_1}\) and \(z_2 = r_2 e^{i \theta_2}\) then

\[z_1 z_2 = r_1 r_2 e^{i (\theta_1 + \theta_2)}. \nonumber \]

This is what mathematicians call trivial to see, just write the multiplication down. In words, the formula says the for \(z_1 z_2\) the magnitudes multiply and the arguments add.

Division

Again it's trivial that

\(\dfrac{r_1 e^{i \theta_1}}{r_2 e^{i \theta_2}} = \dfrac{r_1}{r_2} e^{i (\theta_1 - \theta_2)}.\)

Example \(\PageIndex{1}\): Multiplication by 2\(i\)

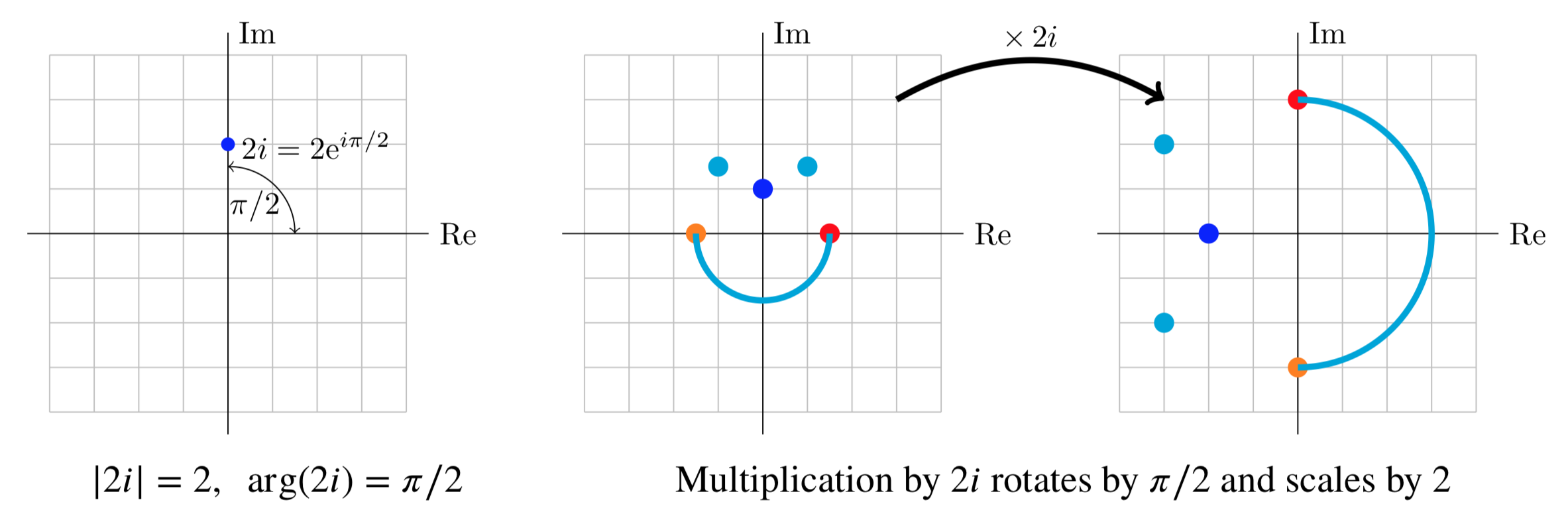
Here’s a simple but important example. By looking at the graph we see that the number \(2i\) has magnitude 2 and argument \(\pi/2\). So in polar coordinates it equals \(2e^{i \pi /2}\). This means that multiplication by \(2i\) multiplies lengths by 2 and add \(\pi/2\) to arguments, i.e. rotates by \(90^{\circ}\). The effect is shown in the figures below

Example \(\PageIndex{2}\): Rasing to a power

Let's compute \((1 + i)^6\) and \((\dfrac{1 + i \sqrt{3}}{2})^3\)

Solution

\(1 + i\) has magnitude = \(\sqrt{2}\) and \(\text{arg} = \pi /4\), so \(1 + i = \sqrt{2} e^{i \pi /4}\). Rasing to a power is now easy:

\((1 + i)^6 = (\sqrt{2} e^{i \pi /4})^6 = 8 e^{6i \pi /4} = 8 e^{3i \pi /2} = -8i\).

Similarly, \(\dfrac{1 + i\sqrt{3}}{2} = e^{i \pi / 3}\), so \((\dfrac{1 + i\sqrt{3}}{2})^3 = (1 \cdot e^{i \pi / 3})^3 = e^{i \pi} = -1\)

Complexification or Complex Replacement

In the next example we will illustrate the technique of complexification or complex replacement. This can be used to simplify a trigonometric integral. It will come in handy when we need to compute certain integrals.

Example \(\PageIndex{3}\)

Use complex replacement to compute

\[I = \int e^x \cos (2x)\ dx. \nonumber \]

Solution

We have Euler's formula

\[e^{2ix} = \cos (2x) + i \sin (2x), \nonumber \]

so \(\cos (2x) = \text{Re} (e^{2ix})\). The complex replacement trick is to replace \(\cos (2x)\) by \(e^{2ix}\). We get (justification below)

\[I_c = \int e^x \cos 2x + ie^x \sin 2x \ dx \nonumber \]

with

\[I = \text{Re} (I_c) \nonumber \]

Computing \(I_c\) is straightforward:

\[I_c = \int e^x e^{i2x}\ dx = \int e^{x(1 + 2i)}\ dx = \dfrac{e^{x(1 + 2i)}}{1 + 2i}. \nonumber \]

Here we will do the computation first in rectangular coordinates. In applications, for example throughout 18.03, polar form is often preferred because it is easier and gives the answer in a more useable form.

\[\begin{array} {rcl} {I_c} & = & {\dfrac{e^{x(1 + 2i)}}{1 + 2i} \cdot \dfrac{1 - 2i}{1 - 2i}} \\ {} & = & {\dfrac{e^x (\cos (2x) + i \sin (2x)) (1 - 2i)}{5}} \\ {} & = & {\dfrac{1}{5} e^x (\cos (2x) + 2 \sin (2x) + i (-2 \cos (2x) + \sin (2x)))} \end{array} \nonumber \]

So,

\[I = \text{Re} (I_c) = \dfrac{1}{5} e^x (\cos (2x) + 2\sin (2x)). \nonumber \]

Justification of complex replacement. The trick comes by cleverly adding a new integral to \(I\) as follows, Let \(J = \int e^x \sin (2x)\ dx\). Then we let

\[I_c = I + iJ = \int e^x (\cos (2x) + i \sin (2x)) \ dx = \int e^x 2^{2ix}\ dx. \nonumber \]

Clearly, by construction, \(\text{Re} (I_c) = I\) as claimed above.

Alternative using polar coordinates to simplify the expression for \(I_c\):

In polar form, we have \(1 + 2i = re^{i \phi}\), where \(r = \sqrt{5}\) and \(\phi = \text{arg} (1 + 2i) = \text{tan}^{-1} (2)\) in the first quadrant. Then:

\(I_c = \dfrac{e^{x(1 + 2i)}}{\sqrt{5} e^{i \phi}} = \dfrac{e^x}{\sqrt{5}} e^{i(2x - \phi)} = \dfrac{e^x}{\sqrt{5}} (\cos (2x - \phi) + i \sin (2x - \phi))\).

Thus,

\[I = \text{Re} (I_c) = \dfrac{e^x}{\sqrt{5}} \cos (2x - \phi). \nonumber \]

\(N\)th roots

We are going to need to be able to find the \(n\)th roots of complex numbers, i.e., solve equations of the form

\[z^N = c, \nonumber \]

where \(c\) is a given complex number. This can be done most conveniently by expressing \(c\) and \(z\) in polar form, \(c = Re^{i \phi}\) and \(z = re^{i \theta}\). Then, upon substituting, we have to solve

\[r^N e^{iN \theta} = Re^{i \phi} \nonumber \]

For the complex numbers on the left and right to be equal, their magnitudes must be the same and their arguments can only differ by an integer multiple of \(2\pi\). This gives

\[r = R^{1/N} \; (N \theta = \phi + 2\pi n), \; where\;n = 0, \pm 1, \pm 2, ... \nonumber \]

Solving for \(\theta\), we have

\[\theta = \dfrac{\phi}{N} + \dfrac{2\pi n}{N}. \nonumber \]

Example \(\PageIndex{4}\)

Find all 5 fifth roots of 2.

Solution

For \(c = 2\), we have \(R = 2\) and \(\phi = 0\), so the fifth roots of 2 are

\(z_n = 2^{1/5} e^{2n \pi i/5}\), where \(n = 0, \pm 1, \pm 2, ...\)

Looking at the right hand side we see that for \(n = 5\) we have \(2^{1/5} e^{2\pi i}\) which is exactly the same as the root when \(n = 0\), i.e. \(2^{1/5} e^{0i}\). Likewise \(n = 6\) gives exactly the same root as \(n = 1\), and so on. This means, we have 5 different roots corresponding to \(n = 0, 1, 2, 3, 4\).

\(z_n = 2^{1/5}, e^{1/5} e^{2\pi i/5}, e^{1/5} e^{4\pi i/5}, e^{1/5} e^{6\pi i/5}, e^{1/5} e^{8\pi i/5}\)

Similarly we can say that in general \(c = Re^{i \phi}\) has \(N\) distinct \(N\) th roots:

\(z_n = r^{1/N} e^{i \phi / N + i 2\pi (n/N)}\) for \(n = 0, 1, 2, ..., N - 1\).

Example \(\PageIndex{5}\)

Find the 4 forth roots of 1.

Solution

We need to solve \(z^4 = 1\), so \(\phi = 0\). So the 4 distinct fourth roots are in polar form

\[z_n = 1, e^{i \pi /2}, e^{i \pi}, e^{i 3 \pi /2} \nonumber \]

and in Cartesian representation

\[z_n = 1, i, -1, -i. \nonumber \]

Example \(\PageIndex{6}\)

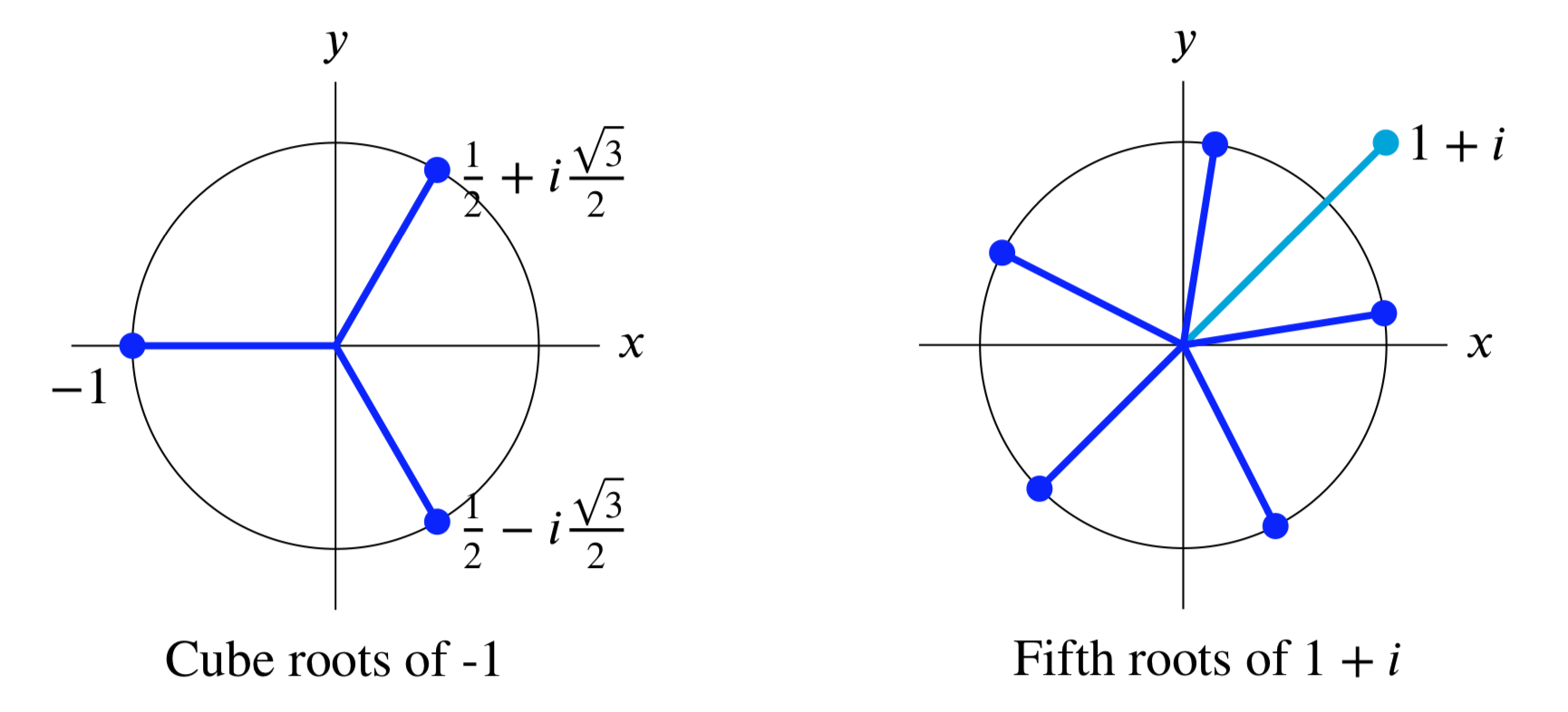
Find the 3 cube roots of -1.

Solution

\(z^2 = -1 = e^{i \pi + i 2 \pi n}\). So, \(z_n = e^{i \pi + i 2 \pi (n/3)}\) and the 3 cube roots are \(e^{i \pi /3}\), \(e^{i \pi}\), \(e^{i 5 \pi /3}\). Since \(\pi /3\) radians is \(60^{\circ}\) we can simplify:

\(e^{i \pi /3} = \cos (\pi / 3) + i \sin (\pi /3) = \dfrac{1}{2} + i \dfrac{\sqrt{3}}{2} \Rightarrow z_n = -1, \dfrac{1}{2} \pm i \dfrac{\sqrt{3}}{2}\)

Example \(\PageIndex{7}\)

Find the 5 fifth roots of \(1 + i\).

Solution

\[z^5 = 1 + i = \sqrt{2} e^{i (\pi / 4 + 2n\pi)} \nonumber \]

for \(n = 0, 1, 2, ...\). So, the 5 fifth roots are

\(2^{1/10} e^{i\pi /20}\), \(2^{1/10} e^{i9\pi /20}\), \(2^{1/10} e^{i17\pi /20}\), \(2^{1/10} e^{i25\pi /20}\), \(2^{1/10} e^{i33\pi /20}\).

Using a calculator we could write these numerically as \(a + bi\), but there is no easy simplification.

Example \(\PageIndex{8}\)

We should check that our technique works as expected for a simple problem. Find the 2 square roots of 4.

Solution

\(z^2 = 4 e^{i2 \pi n}\). So, \(z_n = 2e^{i \pi n}\), with \(n = 0, 1\). So the two roots are \(2e^0 = 2\) and \(2e^{i\pi} = -2\) as expected!

geometry of \(N\)th roots

Looking at the examples above we see that roots are always spaced evenly around a circle centered at the origin. For example, the fifth roots of \(1 + i\) are spaced at increments of \(2\pi / 5\) radians around the circle of radius \(2^{1/5}\).

Note also that the roots of real numbers always come in conjugate pairs.