6.6: Orthogonality of Curves

An important property of harmonic conjugates $u$ and $v$ is that their level curves are orthogonal. We start by showing their gradients are orthogonal.

Lemma $\PageIndex{1}$

Let $z = x + iy$ and suppose that $f(z) = u(x, y) + iv(x, y)$ is analytic. Then the dot product of their gradients is 0, i.e.

$$\Delta u \cdot \Delta v = 0. \nonumber$$

Proof

The proof is an easy application of the Cauchy-Riemann equations.

$$\Delta u \cdot \Delta v = (u_x, u_y) \cdot (v_x, v_y) = u_x v_x + u_y v_y = v_y v_x - v_x v_y = 0 \nonumber$$

In the last step we used the Cauchy-Riemann equations to substitute $v_y$ for $u_x$ and $-v_x$for $u_y$.

The lemma holds whether or not the gradients are 0. To guarantee that the level curves are smooth the next theorem requires that $f'(z) \ne 0$.

Theorem $\PageIndex{1}$

Let $z = x + iy$ and suppose that

$$f(z) = u(x, y) + iv(x, y) \nonumber$$

is analytic. If $f'(z) \ne 0$ then the level curve of $u$ through $(x, y)$ is orthogonal to the level curve $v$ through $(x, y)$.

Proof

The technical requirement that $f'(z) \ne 0$ is needed to be sure that the level curves are smooth. We need smoothness so that it even makes sense to ask if the curves are orthogonal. We’ll discuss this below. Assuming the curves are smooth the proof of the theorem is trivial: We know from 18.02 that the gradient $\nabla u$ is orthogonal to the level curves of $u$ and the same is true for $\nabla v$ and the level curves of $v$. Since, by Lemma 6.6.1, the gradients are orthogonal this implies the curves are orthogonal.

Finally, we show that $f'(z) \ne 0$ means the curves are smooth. First note that

$$f'(z) = u_x(x, y) - iu_y (x, y) = v_y (x, y) + iv_x (x, y). \nonumber$$

Now, since $f'(z) \ne 0$ we know that

$$\nabla u = (u_x, u_y) \ne 0. \nonumber$$

Likewise, $\nabla v \ne 0$. Thus, the gradients are not zero and the level curves must be smooth.

Example $\PageIndex{1}$

The figures below show level curves of $u$ and $v$ for a number of functions. In all cases, the level curves of $u$ are in orange and those of $v$ are in blue. For each case we show the level curves separately and then overlayed on each other.

Example $\PageIndex{2}$

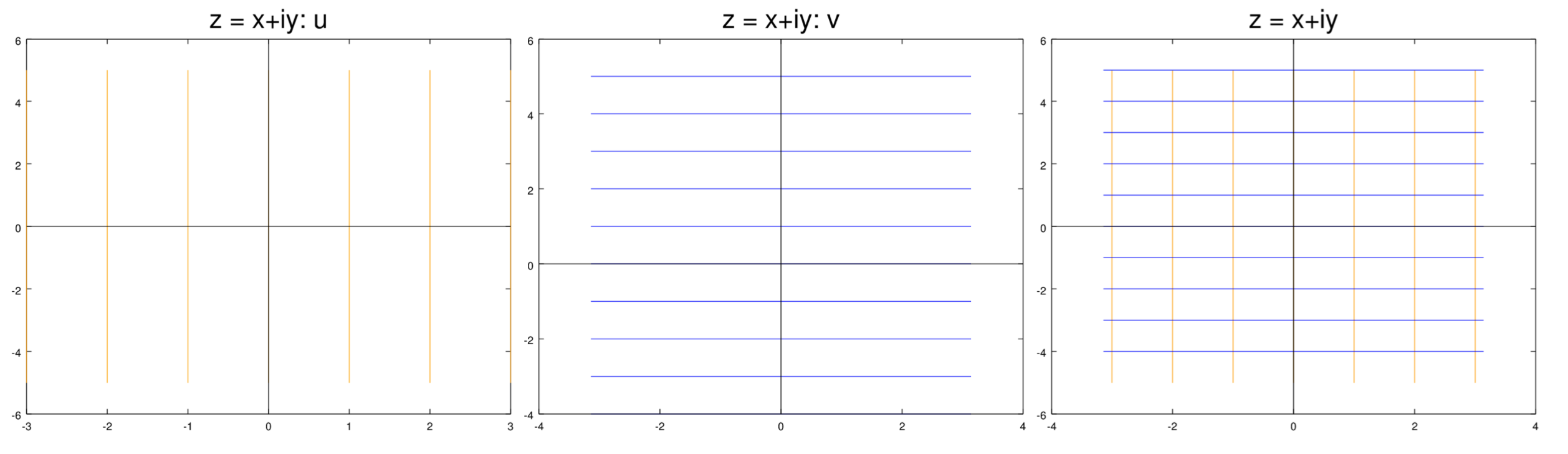
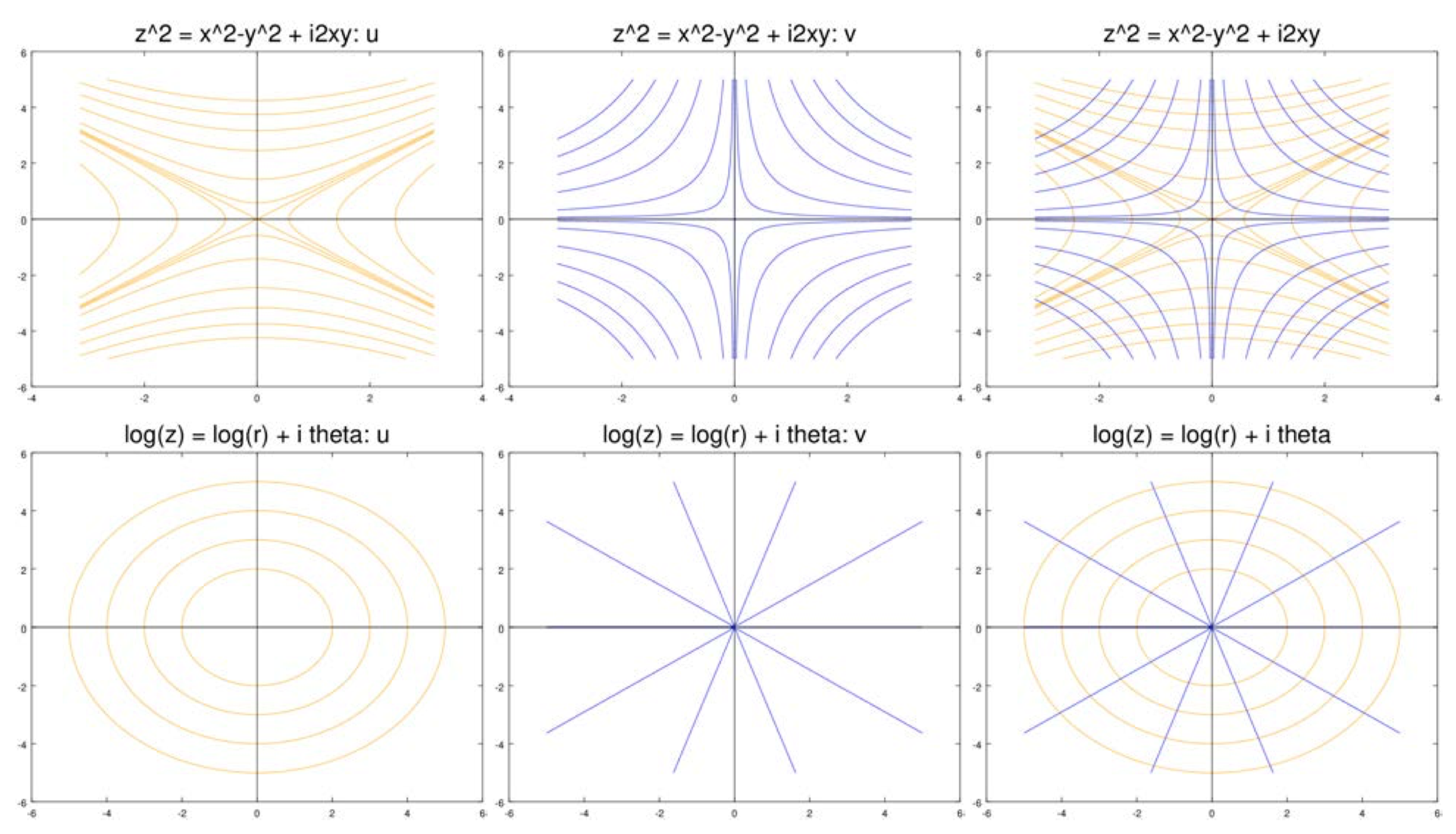
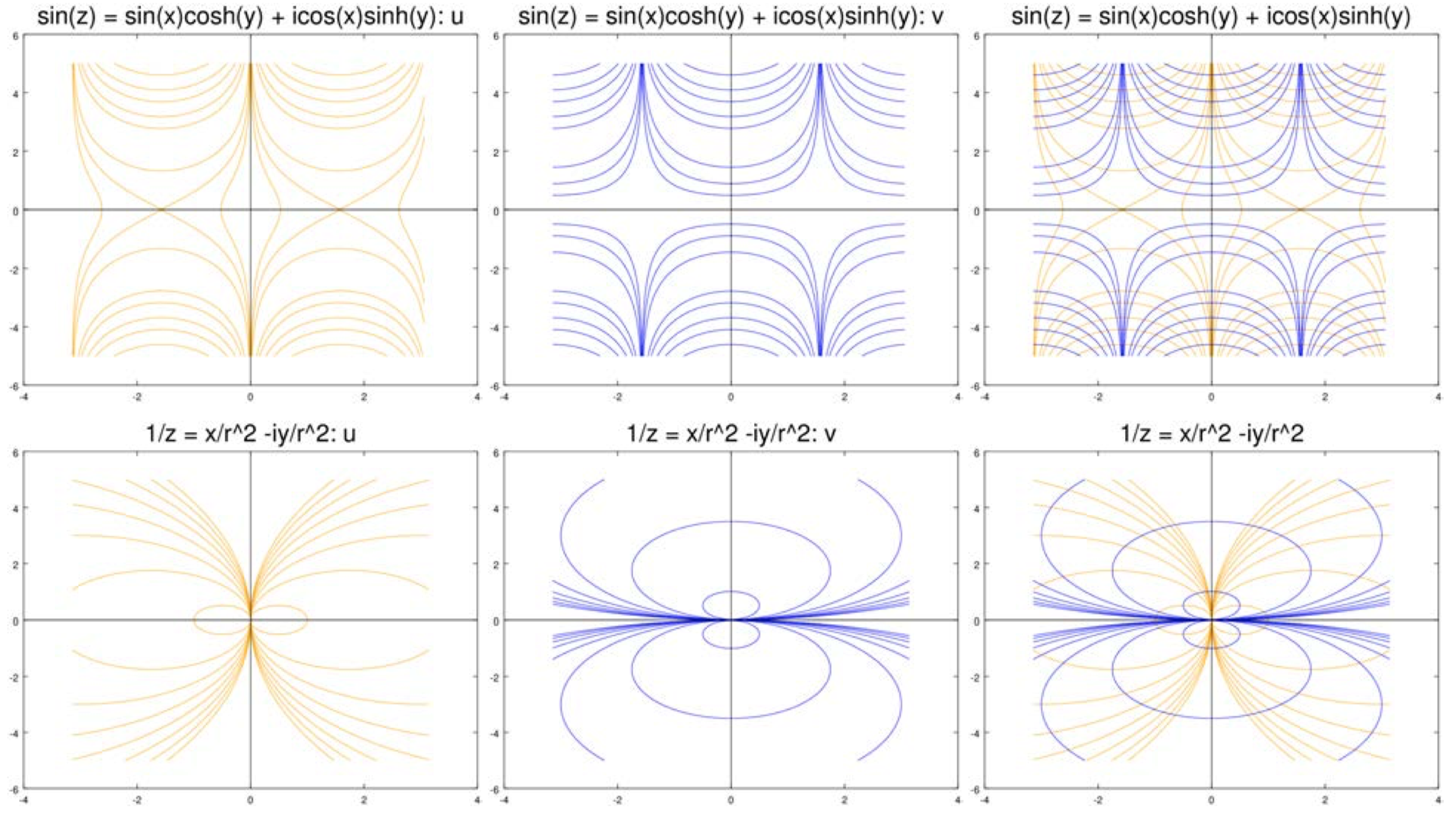
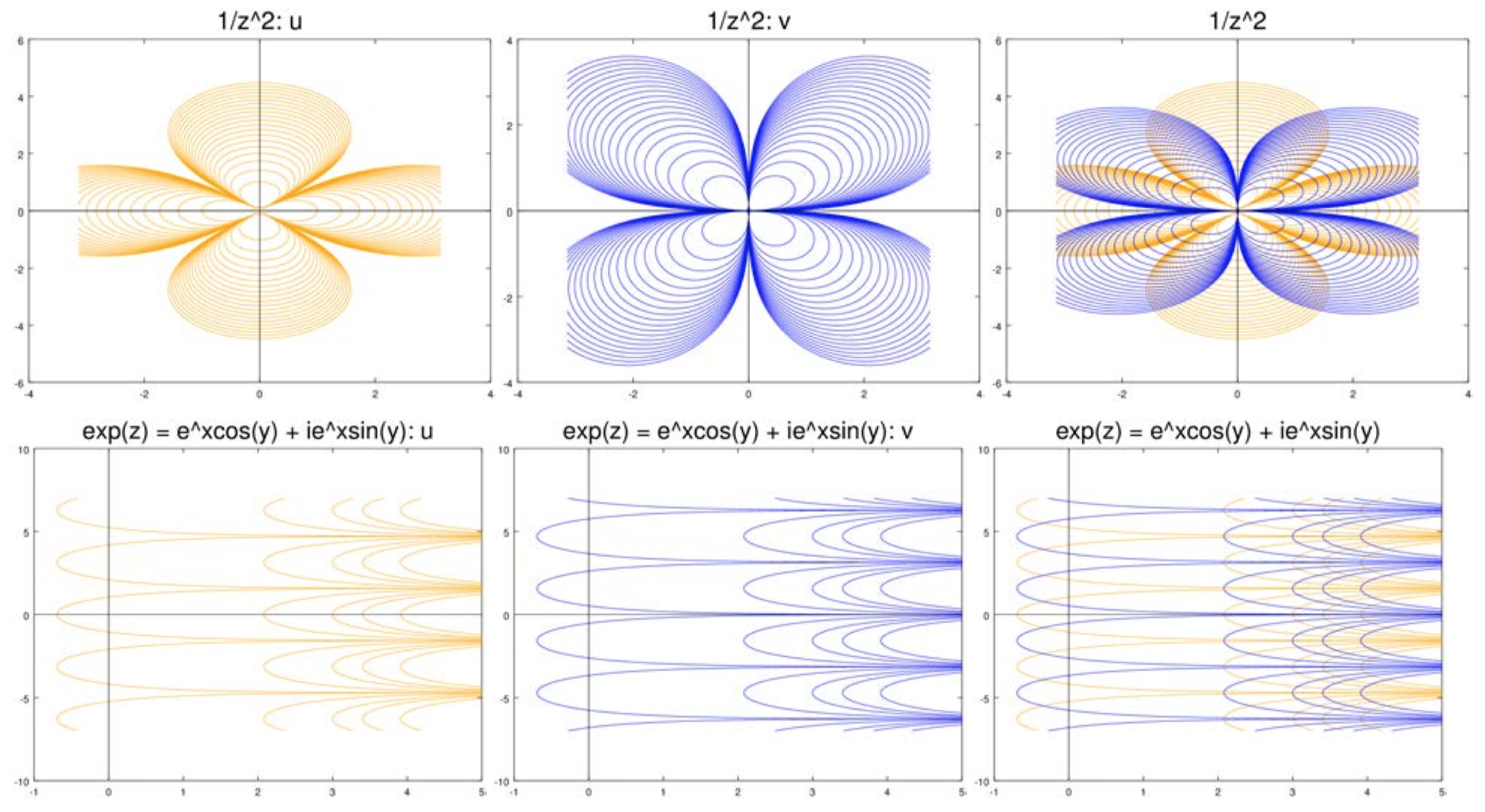
(i) Let

$$f(z) = z^2 = (x^2 - y^2) + i2xy, \nonumber$$

So

$$\nabla u = (2x, -2y) \text{ and } \nabla v = (2y, 2x). \nonumber$$

It's trivial to check that $\nabla u \cdot \nabla v = 0$, so they are orthogonal.

(ii) Let

$$f(z) = \dfrac{1}{z} = \dfrac{x}{r^2} - i \dfrac{y}{r^2}. \nonumber$$

So, it's easy to compute

$$\nabla u = (\dfrac{y^2 - x^2}{r^4}, \dfrac{-2xy}{r^4}) \text{ and } \nabla v = (\dfrac{2xy}{r^4}, \dfrac{y^2 - x^2}{r^4}). \nonumber$$

Again it’s trivial to check that $\nabla u \cdot \nabla v = 0$, so they are orthogonal.

Example $\PageIndex{3}$ Degenerate points: $f'(z) = 0$.

Consider

$$f(z) = z^2 \nonumber$$

From the previous example we have

$$u(x, y) = x^2 - y^2, \ \ \ v(x, y) = 2xy, \ \ \ \nabla u = (2x, -2y), \ \ \ \nabla v = (2y, 2x). \nonumber$$

At $z = 0$, the gradients are both 0 so the theorem on orthogonality doesn’t apply.

Let’s look at the level curves through the origin. The level curve (really the ‘level set’) for

$$u = x^2 - y^2 = 0 \nonumber$$

is the pair of lines $y = \pm x$. At the origin this is not a smooth curve.

Look at the figures for $z^2$ above. It does appear that away from the origin the level curves of $u$ intersect the lines where $v = 0$ at right angles. The same is true for the level curves of $v$ and the lines where $u = 0$. You can see the degeneracy forming at the origin: as the level curves head towards 0 they get pointier and more right angled. So the level curve $u = 0$ is more properly thought of as four right angles. The level curve of $u = 0$, not knowing which leg of $v = 0$ to intersect orthogonally takes the average and comes into the origin at 45$^{\circ}$.