10.2: Degree Centrality
( \newcommand{\kernel}{\mathrm{null}\,}\)
Actors who have more ties to other actors may be in advantaged positions. Because they have many ties, they may have alternative ways to satisfy needs, and hence are less dependent on other individuals. Because they have many ties, they may have access to, and be able to call on, more of the resources of the network as a whole. Because they have many ties, they are often third parties and deal makers in exchanges among others, and are able to benefit from this brokerage. So, a very simple, but often very effective measure of an actor's centrality and power potential is their degree.
In undirected data, actors differ from one another only in how many connections they have. With directed data, however, it can be important to distinguish centrality based on in-degree from centrality based on out-degree. If an actor receives many ties, they are often said to be prominent, or to have high prestige. That is, many other actors seek to direct ties to them, and this may indicate their importance. Actors who have unusually high out-degree are actors who are able to exchange with many others, or make many others aware of their views. Actors who display high out-degree centrality are often said to be influential actors.
Recall Knoke's data on information exchanges among organizations operating in the social welfare field, shown in Figure 10.4.
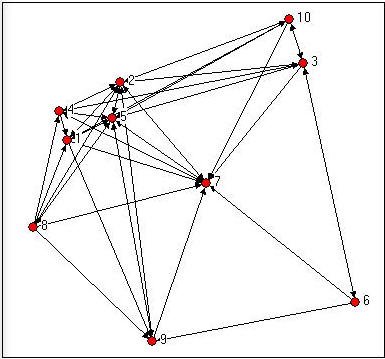
Figure 10.4: Knoke's information exchange network
Simply counting the number of in-ties and out-ties of the nodes suggests that certain actors are more "central" here (e.g. 2, 5, 7). It also appears that this network as a whole may have a group of central actors, rather than a single "star". We can see "centrality" as an attribute of individual actors as a consequence of their position; we can also see how "centralized" the graph as a whole is - how unequal is the distribution of centrality.
Freeman's Approach
Linton Freeman (one of the authors of UCINET) developed basic measures of the centrality of actors based on their degree, and the overall centralization of graphs.
Figure 10.5 shows the output of Network>Centrality>Degree applied to out-degrees and to the in-degrees of the Knoke information network. The centrality can also be computed ignoring the direction of ties (i.e. a tie in either direction is counted as a tie).
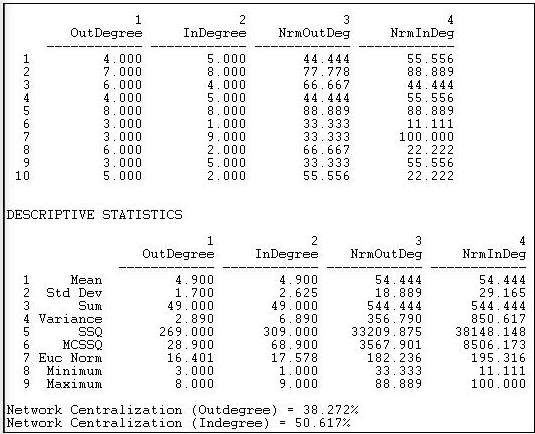
Figure 10.5: Freeman degree centrality and graph centralization of Knoke information network
Actors #5 and #2 have the greatest out-degrees, and might be regarded as the most influential (though it might matter to whom they are sending information, this measure does not take that into account). Actors #5 and #2 are joined by #7 (the newspaper) when we examine in-degree. That other organizations share information with these three would seem to indicate a desire on the part of others to exert influence. This is an act of deference, or a recognition that the positions of actors 5, 2, and 7 might be worth trying to influence. If we were interested in comparing across networks of different sizes or densities, it might be useful to "standardize" the measures of in-degree and out-degree. In the last two columns of the first panel of results above, all the degree counts have been expressed as percentages of the number of actors in the network, less one (ego).
The next panel of results speaks to the "meso" level or analysis. That is, what does the distribution of the actor's degree centrality scores look like? On the average, actors have a degree of 4.9, which is quite high, given that there are only nine other actors. We see that the range of in-degree is slightly larger (minimum and maximum) than that of out-degree, and that there is more variability across the actors in in-degree than out-degree (standard deviations and variances). The range and variability of degree (and other network properties) can be quite important, because it describes whether the population is homogeneous or heterogeneous in structural positions. One could examine whether the variability is high or low relative to the typical scores by calculating the coefficient of variation (standard deviation divided by mean, times 100) for in-degree and out-degree. By the rules of thumb that are often used to evaluate coefficients of variation, the current values (35 for out-degree and 53 for in-degree) are moderate. Clearly, however, the population is more homogeneous with regard to out-degree (influence) than with regard to in-degree (prominence).
The last bit of information provided by the output above are Freeman's graph centralization measures, which describe the population as a whole - the macro level. These are very useful statistics, but require a bit of explanation.
Remember our "star" network from the discussion above (if not, go review it)? The star network is the most centralized or most unequal possible network for any number of actors. In the star network, all the actors but one have degree of one, and the "star" has degree of the number of actors, less one. Freeman felt that it would be useful to express the degree of variability in the degrees of actors in our observed network as a percentage of that in a star network of the same size. This is how the Freeman graph centralization measures can be understood: they express the degree of inequality or variance in our network as a percentage of that of a perfect star network of the same size. In the current case, the out-degree graph centralization is 51% and the in-degree graph centralization 38% of these theoretical maximums. We would arrive at the conclusion that there is a substantial amount of concentration or centralization in this whole network. That is, the power of individual actors varies rather substantially, and this means that, overall, positional advantages are rather unequally distributed in this network.
Bonacich's Approach
Philip Bonacich proposed a modification of the degree centrality approach that has been widely accepted as superior to the original measure. Bonacich's idea, like most good ones, is pretty simple. The original degree centrality approach argues that actors who have more connections are more likely to be powerful because they can directly affect more other actors. This makes sense, but having the same degree does not necessarily make actors equally important.
Suppose that Bill and Fred each have five close friends. Bill's friends, however, happen to be pretty isolated folks, and don't have many other friends, save Bill. In contrast, Fred's friends each also have lots of friends, who have lots of friends, and so on. Who is more central? We would probably agree that Fred is, because the people he is connected to are better connected than Bill's people. Bonacich argued that one's centrality is a function of how many connections one has, and how many of the connections the actors in the neighborhood had.
While we have argued that more central actors are more likely to be more powerful actors, Bonacich questioned this idea. Compare Bill and Fred again. Fred is clearly more central, but is he more powerful? One argument would be that one is likely to be more influential if one is connected to central others - because one can quickly reach a lot of other actors with one's message. But if the actors that you are connected to are, themselves, well connected, they are not highly dependent on you - they have many contacts, just as you do. If, on the other hand, the people to whom you are connected are not, themselves, well connected, then they are dependent on you. Bonacich argued that being connected to connected others makes an actor central, but not powerful. Somewhat ironically, being connected to others that are not well connected makes one powerful, because these other actors are dependent on you - whereas well connected actors are not.
Bonacich proposed that both centrality and power were a function of the connections of the actors in one's neighborhood. The more connections the actors in your neighborhood have, the more central you are. The fewer the connections the actors in your neighborhood, the more powerful you are. There would seem to be a problem with building an algorithm to capture these ideas. Suppose A and B are connected. Actor A's power and centrality are functions of her own connections, and also the connections of actor B. Similarly, actor B's power and centrality depend on actor A's. So, each actor's power and centrality depends on each other actor's power simultaneously.
There is a way out of this chicken-and-egg type of problem. Bonacich showed that, for symmetric systems, an iterative estimation approach to solving this simultaneous equations problem would eventually converge to a single answer. One begins by giving each actor an estimated centrality equal to their own degree, plus a weighted function of the degrees of the actors to whom they were connected. Then, we do this again, using the first estimates (i.e. we again give each actor an estimated centrality equal to their own score plus the first scores of those to whom they are connected). As we do this numerous times, the relative sizes (not the absolute sizes) of all actors' scores will come to be the same. The scores can then be re-expressed by scaling by constants.
Let's examine the centrality and power scores for our information exchange data. First, we examine the case where the score for each actor is a positive function of their own degree, and the degrees of the others to whom they are connected. We do this by selecting a positive weight of the "attenuation factor" or Beta parameter) in the dialog of Network>Centrality>Power, as shown in Figure 10.6.

Figure 10.6: Dialog for computing Bonacich's power measures
The "attenuation factor" indicates the effect of one's neighbor's connections on ego's power. Where the attenuation factor is positive (between zero and one), being connected to neighbors with more connections makes one powerful. This is a straightforward extension of the degree centrality idea.
Bonacich also had a second idea about power, based on the notion of "dependency". If ego has neighbors who do not have many connections to others, those neighbors are likely to be dependent on ego, making ego more powerful. Negative values of the attenuation factor (between zero and negative one) compute power based on this idea.
Figures 10.7 and 10.8 show the Bonacich measures for positive and negative beta values.

Figure 10.7: Network>Centrality>Power with beta = +0.50
If we look at the absolute value of the index scores, we see the familiar story. Actors #5, and #2 are clearly the most central. This is because they have high degree, and because they are connected to each other, and to other actors with high degree. Actors 8 and 10 also appear to have high centrality by this measure - this is a new result. In these cases, it is because the actors are connected to all of the other high degree points. These actors don't have extraordinary numbers of connections, but they have "the right connections".
Let's take a look at the power side of the index, which is calculated by the same algorithm, but gives negative weights to connections with well connected others, and positive weights for connections to weakly connected others.
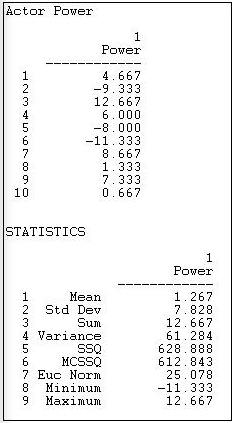
Figure 10.8: Network>Centrality>Power with beta = -0.50
Not surprisingly, these results are very different from many of the others we've examined. With a negative attenuation parameter, we have a quite different definition of power - having weak neighbors, rather than strong ones. Actors numbers 2 and 6 are distinguished because their ties are mostly ties to actors with high degree - making actors 2 and 6 "weak" by having powerful neighbors. Actors 3, 7, and 9 have more ties to neighbors who have few ties - making them "strong" by having weak neighbors. You might want to scan the diagram again to see if you can see these differences.
The Bonacich approach to degree-based centrality and degree-based power are fairly natural extensions of the idea of degree centrality based on adjacencies. One is simply taking into account the connections of one's connections, in addition to one's own connections. The notion that power arises from connection to weak others, as opposed to strong others is an interesting one, and points to yet another way in which the positions of actors in network structures endow them with different potentials.


