13.6: Reaction-Diffusion Systems
- Page ID
- 7848
Finally, I would like to introduce reaction-diffusion systems, a particular class of continuous field models that have been studied extensively. They are continuous field models whose equations are made of only reaction terms and diffusion terms, as shown below:
\[\dfrac{\partial{f_1}}{\partial{t}} =R_1(f_1,f_2,...,f_n) + D_1∇^{2}f_1 \label{(13.53)} \]
\[\dfrac{\partial{f_2}}{\partial{t}} = R_2 (f_1,f_2,...,f_n) + D_2∇^{2}f_2 \label{(13.54)} \]
\[ \vdots \nonumber \]
\[\dfrac{\partial{f_n}}{\partial{t}} =R_n(f_1,f_2,...,f_n) + D_n∇^{2}f_n \label{(13.55)} \]
Reaction terms (\(R_i(...)\)) describe only local dynamics, without any spatial derivatives involved. Diffusion terms (\(D_i∇^{2}f_i\)) are strictly limited to the Laplacian of the state variable itself. Therefore, any equations that involve non-diffusive spatial movement (e.g., chemotaxis) are not reaction-diffusion systems.
There are several reasons why reaction-diffusion systems have been a popular choice among mathematical modelers of spatio-temporal phenomena. First, their clear separation between non-spatial and spatial dynamics makes the modeling and simulation tasks really easy. Second, limiting the spatial movement to only diffusion makes it quite straightforward to expand any existing non-spatial dynamical models into spatially distributed ones. Third, the particular structure of reaction-diffusion equations provides an easy shortcut in the stability analysis (to be discussed in the next chapter). And finally, despite the simplicity of their mathematical form, reaction-diffusion systems can show strikingly rich, complex spatio-temporal dynamics. Because of these properties, reaction diffusion systems have been used extensively for modeling self-organization of spatial patterns. There are even specialized software applications available exactly to simulate reaction-diffusion systems3.
Extend the following non-spatial models into spatially distributed ones as reaction-diffusion systems by adding diffusion terms. Then simulate their behaviors in Python.
- Motion of a pendulum (Eq.(6.2.1)): This creates a spatial model of locally coupled nonlinear oscillators.
- Susceptible-Infected-Recovered (SIR) model (Exercise 7.1.3): This creates a spatial model of epidemiological dynamics.
In what follows, we will review a few well-known reaction-diffusion systems to get a glimpse of the rich, diverse world of their dynamics.
Turing Pattern Formation
As mentioned at the very beginning of this chapter, Alan Turing’s PDE models were among the first reaction-diffusion systems developed in the early 1950s [44]. A simple linear version of Turing’s equations is as follows:
\[\dfrac{\partial{u}}{\partial{t}} =a(u-h) +b(v-k) +D_{u}\Delta^{2}u \label{13.56} \]
\[\dfrac{\partial{u}}{\partial{t}} =c(u-h) +d(v-k) +D_{u}\Delta^{2}u \label{13.57} \]
The state variables \(u\) and \(v\) represent concentrations of two chemical species. \(a, b, c,\) and \(d\) are parameters that determine the behavior of the reaction terms, while \(h\) and \(k\) are constants. Finally, \(D_u\) and \(D_v\) are diffusion constants.
If the diffusion terms are ignored, it is easy to show that this system has only one equilibrium point, (\(u_eq,v_eq) = (h,k)\). This equilibrium point can be stable for many parameter values for \(a, b, c,\) and \(d\). What was most surprising in Turing’s findings is that, even for such stable equilibrium points, introducing spatial dimensions and diffusion terms to the equations may destabilize the equilibrium, and thus the system may spontaneously self-organize into a non-homogeneous pattern. This is called diffusion-induced instability or Turing instability. A sample simulation result is shown in Fig. 13.6.1.
The idea of diffusion-induced instability is quite counter-intuitive. Diffusion is usually considered a random force that destroys any structure into a homogenized mess, yet in this particular model, diffusion is the key to self-organization! What is going on? The trick is that this system has two different diffusion coefficients, \(D_u\) and \(D_v\), and their difference plays a key role in determining the stability of the system’s state. This will be discussed in more detail in the next chapter.
There is one thing that needs particular attention when you are about to simulate Turing’s reaction-diffusion equations. The Turing pattern formation requires small random perturbations (noise) to be present in the initial configuration of the system; otherwise there would be no way for the dynamics to break spatial symmetry to create non-homogeneous patterns. In the meantime, such initial perturbations should be small enough so that they won’t immediately cause numerical instabilities in the simulation. Here is a sample code for simulating Turing pattern formation with a suggested level of initial perturbations, using the parameter settings shown in Fig. 13.6.1:
This simulation starts from an initial configuration \((u(x,y),v(x,y)) ≈ (1,1) = (h,k)\), which is the system’s homogeneous equilibrium state that would be stable without diffusion terms. Run the simulation to see how patterns spontaneously self-organize!
Conduct simulations of the Turing pattern formation with several different parameter settings, and discuss how the parameter variations (especially for the diffusion constants) affect the resulting dynamics.
Discretize the Keller-Segel slime mold aggregation model (Eqs. (13.4.13) and (13.4.14)) (although this model is not a reaction-diffusion system, this is the perfect time for you to work on this exercise because you can utilize Code 13.8). Implement its simulation code in Python, and conduct simulations with \(µ = 10^{−4}\), \(D = 10^{−4}\), \(f = 1\), and \(k = 1\), while varying \(χ\) as a control parameter ranging from \(0\) to \(10^{−3}\). Use \(a = 1\) and \(c = 0\) as initial conditions everywhere, with small random perturbations added to them.
Belousov-Zhabotinsky Reaction
The Belousov-Zhabotinsky reaction, or BZ reaction for short, is a family of oscillatory chemical reactions first discovered by Russian chemist Boris Belousov in the 1950s and then later analyzed by Russian-American chemist Anatol Zhabotinsky in the 1960s. One of the common variations of this reaction is essentially an oxidation of malonic acid (\(CH_{2}(COOH)_{2}\)) by an acidified bromate solution, yet this process shows nonlinear oscillatory behaviorf or a substantial length of time before eventually reaching chemical equilibrium. The actual chemical mechanism is quite complex, involving about 30 different chemicals. Moreover, if this chemical solution is put into a shallow petri dish, the chemical oscillation starts in different phases at different locations. Interplay between the reaction and the diffusion of the chemicals over the space will result in the self-organization of dynamic traveling waves (Figure \(\PageIndex{2}\)), just like those seen in the excitable media CA model in Section 11.5.
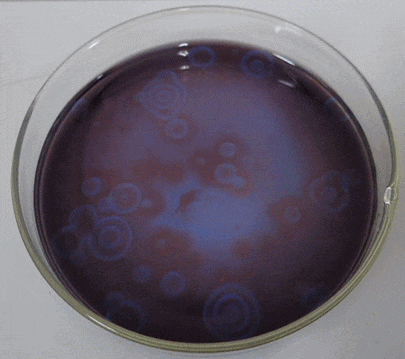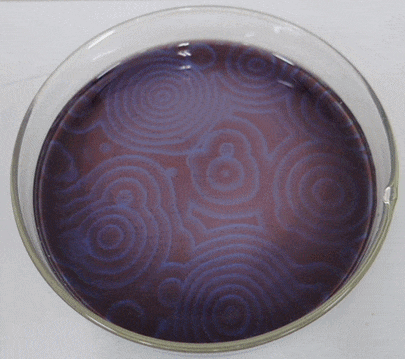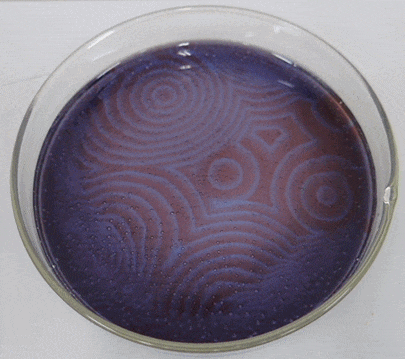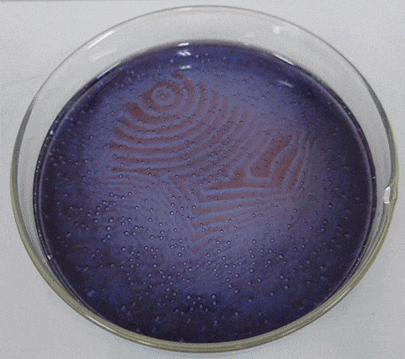
A simplified mathematical model called the “Oregonator” was among the first to describe the dynamics of the BZ reaction in a simple form [50]. It was originally proposed as a non-spatial model with three state variables, but the model was later simplified to have just two variables and then extended to spatial domains [51]. Here are the simplified “Oregonator” equations:
\[ \begin{align} \epsilon{\dfrac{\partial{u}}{\partial{t}}} &= u(1-u)-\dfrac{u-q}{u+q}fv + D_{u}\Delta^{2}u \label{(13.58)} \\[4pt] \dfrac{∂v}{∂t} &=u-v + D_{u}\Delta^{2}v \label{(13.59)} \end{align} \]
Here, \(u\) and \(v\) represent the concentrations of two chemical species. If you carefully examine the reaction terms of these equations, you will noticethat the presenceof chemical \(u\) has a positive effect on both \(u\) and \(v\), while the presence of chemical \(v\) has a negative effect on both. Therefore, these chemicals are called the “activator” and the “inhibitor,” respectively. Similar interactions between the activator and the inhibitor were also seen in the Turing pattern formation, but the BZ reaction system shows nonlinear chemical oscillation. This causes the formation of traveling waves. Sometimes those waves can form spirals if spatial symmetry is broken by stochastic factors. A sample simulation result is shown in Fig. 13.6.3.
Implement a simulator code of the “Oregonator” model of the BZ reaction in Python. Then conduct simulations with several different parameter settings, and discuss what kind of conditions would be needed to produce traveling waves.
Gray-Scott Pattern Formation
The final example is the Gray-Scott model, another very well-known reaction-diffusion system studied and popularized by John Pearson in the 1990s [52], based on a chemical reaction model developed by Peter Gray and Steve Scott in the 1980s [53, 54, 55]. The model equations are as follows:
\[ \dfrac{∂u}{∂t} =F(1-u) -uv^{2} +D_{u}\Delta^{2}u \label{(13.60)} \]
\[\dfrac{∂v}{∂t} =-(F+k)v +uv^{2}+ D_{u}\Delta^{2}v \label{(13.61)} \]
The reaction terms of this model assumes the following autocatalytic reaction (i.e., chemical reaction for which the reactant itself serves as a catalyst):
\[u+2v \rightarrow 3v \label{(13.62)} \]
This reaction takes one molecule of \(u\) and turns it into one molecule of \(v\), with help of two other molecules of \(v\) (hence, autocatalysis). This is represented by the second term in each equation. In the meantime, \(u\) is continuously replenished from the external source up to 1 (the first term of the first equation) at feed rate \(F\), while \(v\) is continuously removed from the system at a rate slightly faster than \(u\) ’s replenishment (\(F +k \)seen in the first term of the second equation). \(F\) and \(k\) are the key parameters of this model.
It is easy to show that, if the diffusion terms are ignored, this system always has an equilibrium point at \((u_{eq},v_{eq}) = (1,0)\) (which is stable for any positive \(F\) and \(k\)). Surprisingly, however, this model may show very exotic, biological-looking dynamics if certain spatial patterns are placed into the above equilibrium. Its behaviors are astonishingly rich, even including growth, division, and death of “cells” if the parameter values and initial conditions are appropriately chosen. See Fig. 13.6.4 to see only a few samples of its wondrous dynamics!
Implement a simulator code of the Gray-Scott model in Python. Then conduct simulations with several different parameter settings and discuss how the parameters affect the resulting patterns.
Figure \(\PageIndex{4}\): (Next page) Samples of patterns generated by the Gray-Scott model with \(D_u = 2 × 10^{−5}\) and \(D_v = 10^{−5}\). The concentration of chemical \(u\) is plotted in grayscale (brighter = greater, only in this figure). Time flows from left to right. The parameter values of \(F\) and \(k\) are shown above each simulation result. The initial conditions are the homogeneous equilibrium \((u,v) = (1,0)\) everywhere in the space, except at the center where the local state is reversed such that \((u,v) = (0,1)\).
3For example, check out Ready (https://code.google.com/p/reaction-diffusion/).


