10.5: Multiply Polynomials (Part 2)
- Page ID
- 7268
Using the FOIL Method
Remember that when you multiply a binomial by a binomial you get four terms. Sometimes you can combine like terms to get a trinomial, but sometimes there are no like terms to combine. Let's look at the last example again and pay particular attention to how we got the four terms.
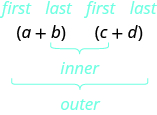
\[\begin{split} (x + 2)&(x - y) \\ x^{2} - xy &+ 2x - 2y \end{split}\]
Where did the first term, x2, come from?
It is the product of x and x, the first terms in (x + 2) and (x − y).
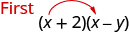
The next term, −xy, is the product of x and − y, the two outer terms.
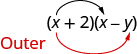
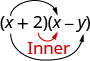
The third term, +2x, is the product of 2 and x, the two inner terms.
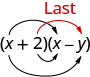
And the last term, −2y, came from multiplying the two last terms.
We abbreviate “First, Outer, Inner, Last” as FOIL. The letters stand for ‘First, Outer, Inner, Last’. The word FOIL is easy to remember and ensures we find all four products. We might say we use the FOIL method to multiply two binomials.
Let's look at (x + 3)(x + 7) again. Now we will work through an example where we use the FOIL pattern to multiply two binomials.
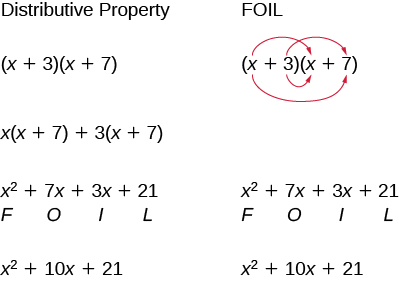
Multiply using the FOIL method: (x + 6)(x + 9).
Solution
| Step 1: Multiply the First terms. | 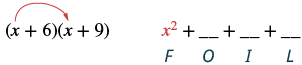 |
| Step 2: Multiply the Outer terms. | 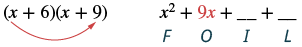 |
| Step 3: Multiply the Inner terms. | 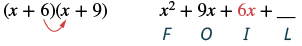 |
| Step 4: Multiply the Last terms. | 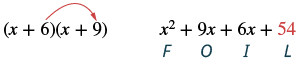 |
| Step 5: Combine like terms, when possible. | x2 + 15x + 54 |
Multiply using the FOIL method: (x + 7)(x + 8).
- Answer
-
\(x^2+15x+56 \)
Multiply using the FOIL method: (y + 14)(y + 2).
- Answer
-
\(y^2+16y+28\)
We summarize the steps of the FOIL method below. The FOIL method only applies to multiplying binomials, not other polynomials!
Step 1. Multiply the First terms.
Step 2. Multiply the Outer terms.
Step 3. Multiply the Inner terms.
Step 4. Multiply the Last terms.
Step 5. Combine like terms, when possible.

Multiply: (y − 8)(y + 6).
Solution
| Step 1: Multiply the First terms. | 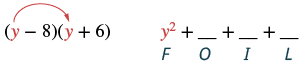 |
| Step 2: Multiply the Outer terms. | 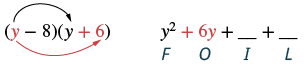 |
| Step 3: Multiply the Inner terms. | 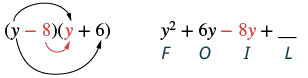 |
| Step 4: Multiply the Last terms. |  |
| Step 5: Combine like terms, when possible. | y2 - 2y - 48 |
Multiply: (y − 3)(y + 8).
- Answer
-
\(y^2+5y-24 \)
Multiply: (q − 4)(q + 5).
- Answer
-
\(q^2+q-20 \)
Multiply: (2a + 3)(3a − 1).
Solution
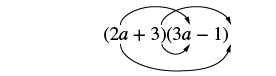 |
|
| Multiply the First terms. | 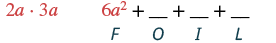 |
| Multiply the Outer terms. | 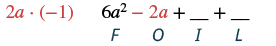 |
| Multiply the Inner terms. | 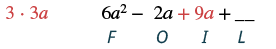 |
| Multiply the Last terms. | 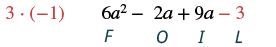 |
| Combine like terms. | 6a2 + 7a - 3 |
Multiply: (4a + 9)(5a − 2).
- Answer
-
\(20a^2+37a-18 \)
Multiply: (7x + 4)(7x − 8).
- Answer
-
\( 49x^2-28x-32\)
Multiply: (5x − y)(2x − 7).
Solution
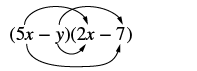 |
|
| Multiply the First terms. | 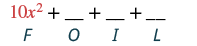 |
| Multiply the Outer terms. | 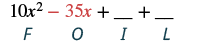 |
| Multiply the Inner terms. | 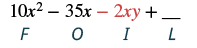 |
| Multiply the Last terms. | 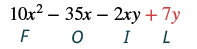 |
| Combine like terms. There are none. | 10x2 - 35x - 2xy + 7y |
Multiply: (12x − y)(x − 5).
- Answer
-
\(12 x^{2}-60 x-x y+5 y \)
Multiply: (6a − b)(2a − 9).
- Answer
-
\(12 a^{2}-54 a-2 a b+9 b \)
Using the Vertical Method
The FOIL method is usually the quickest method for multiplying two binomials, but it works only for binomials. You can use the Distributive Property to find the product of any two polynomials. Another method that works for all polynomials is the Vertical Method. It is very much like the method you use to multiply whole numbers. Look carefully at this example of multiplying two-digit numbers.

You start by multiplying 23 by 6 to get 138. Then you multiply 23 by 4, lining up the partial product in the correct columns. Last, you add the partial products. Now we'll apply this same method to multiply two binomials.
Multiply using the vertical method: (5x − 1)(2x − 7).
Solution
It does not matter which binomial goes on the top. Line up the columns when you multiply as we did when we multiplied 23(46).
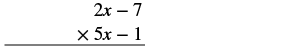 |
|
| Multiply 2x − 7 by −1. |  |
| Multiply 2x − 7 by 5x. |  |
| Add like terms. | 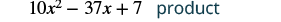 |
Notice the partial products are the same as the terms in the FOIL method.
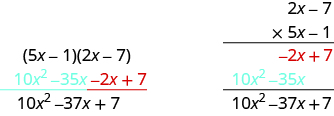
Multiply using the vertical method: (4m − 9)(3m − 7).
- Answer
-
\( 12 m^{2}-55 m+63\)
Multiply using the vertical method: (6n − 5)(7n − 2).
- Answer
-
\(42 n^{2}-47 n+10 \)
We have now used three methods for multiplying binomials. Be sure to practice each method, and try to decide which one you prefer. The three methods are listed here to help you remember them.
To multiply binomials, use the:
- Distributive Property
- FOIL Method
- Vertical Method
Remember, FOIL only works when multiplying two binomials.
Multiply a Trinomial by a Binomial
We have multiplied monomials by monomials, monomials by polynomials, and binomials by binomials. Now we're ready to multiply a trinomial by a binomial. Remember, the FOIL method will not work in this case, but we can use either the Distributive Property or the Vertical Method. We first look at an example using the Distributive Property.
Multiply using the Distributive Property: (x + 3)(2x2 − 5x + 8).
Solution
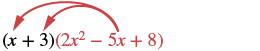 |
|
| Distribute. | 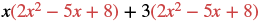 |
| Multiply. | 2x3 − 5x2 + 8x + 6x2 − 15x + 24 |
| Combine like terms. | 2x3 + x2 − 7x + 24 |
Multiply using the Distributive Property: (y − 1)(y2 − 7y + 2).
- Answer
-
\( y^{3}-8 y^{2}+9 y-2\)
Multiply using the Distributive Property: (x + 2)(3x2 − 4x + 5).
- Answer
-
\( 3 x^{3}+2 x^{2}-3 x+10\)
Now let's do this same multiplication using the Vertical Method.
Multiply using the Vertical Method: (x + 3)(2x2 − 5x + 8).
Solution
It is easier to put the polynomial with fewer terms on the bottom because we get fewer partial products this way.
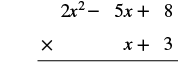 |
|
| Multiply (2x2 − 5x + 8) by 3. | 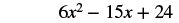 |
| Multiply (2x2 − 5x + 8) by x. | 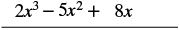 |
| Add like terms. | 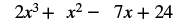 |
Multiply using the Vertical Method: (y − 1)(y2 − 7y + 2).
- Answer
-
\(y^{3}-8 y^{2}+9 y-2 \)
Multiply using the Vertical Method: (x + 2)(3x2 − 4x + 5).
- Answer
-
\( 3 x^{3}+2 x^{2}-3 x+10\)
Multiply Monomials
Multiply Polynomials
Multiply Polynomials 2
Multiply Polynomials Review
Multiply Polynomials Using the Distributive Property
Multiply Binomials
Practice Makes Perfect
Multiply a Polynomial by a Monomial
In the following exercises, multiply.
- 4(x + 10)
- 6(y + 8)
- 15(r − 24)
- 12(v − 30)
- −3(m + 11)
- −4(p + 15)
- −8(z − 5)
- −3(x − 9)
- u(u + 5)
- q(q + 7)
- n(n2 − 3n)
- s(s2 − 6s)
- 12x(x − 10)
- 9m(m − 11)
- −9a(3a + 5)
- −4p(2p + 7)
- 6x(4x + y)
- 5a(9a + b)
- 5p(11p − 5q)
- 12u(3u − 4v)
- 3(v2 + 10v + 25)
- 6(x2 + 8x + 16)
- 2n(4n2 − 4n + 1)
- 3r(2r2 − 6r + 2)
- −8y(y2 + 2y − 15)
- −5m(m2 + 3m − 18)
- 5q3(q2 − 2q + 6)
- 9r3(r2 − 3r + 5)
- −4z2(3z2 + 12z − 1)
- −3x2(7x2 + 10x − 1)
- (2y − 9)y
- (8b − 1)b
- (w − 6) • 8
- (k − 4) • 5
Multiply a Binomial by a Binomial
In the following exercises, multiply the following binomials using: (a) the Distributive Property (b) the FOIL method (c) the Vertical method
- (x + 4)(x + 6)
- (u + 8)(u + 2)
- (n + 12)(n − 3)
- (y + 3)(y − 9)
In the following exercises, multiply the following binomials. Use any method.
- (y + 8)(y + 3)
- (x + 5)(x + 9)
- (a + 6)(a + 16)
- (q + 8)(q + 12)
- (u − 5)(u − 9)
- (r − 6)(r − 2)
- (z − 10)(z − 22)
- (b − 5)(b − 24)
- (x − 4)(x + 7)
- (s − 3)(s + 8)
- (v + 12)(v − 5)
- (d + 15)(d − 4)
- (6n + 5)(n + 1)
- (7y + 1)(y + 3)
- (2m − 9)(10m + 1)
- (5r − 4)(12r + 1)
- (4c − 1)(4c + 1)
- (8n − 1)(8n + 1)
- (3u − 8)(5u − 14)
- (2q − 5)(7q − 11)
- (a + b)(2a + 3b)
- (r + s)(3r + 2s)
- (5x − y)(x − 4)
- (4z − y)(z − 6)
Multiply a Trinomial by a Binomial
In the following exercises, multiply using (a) the Distributive Property and (b) the Vertical Method.
- (u + 4)(u2 + 3u + 2)
- (x + 5)(x2 + 8x + 3)
- (a + 10)(3a2 + a − 5)
- (n + 8)(4n2 + n − 7)
In the following exercises, multiply. Use either method.
- (y − 6)(y2 − 10y + 9)
- (k − 3)(k2 − 8k + 7)
- (2x + 1)(x2 − 5x − 6)
- (5v + 1)(v2 − 6v − 10)
Everyday Math
- Mental math You can use binomial multiplication to multiply numbers without a calculator. Say you need to multiply 13 times 15. Think of 13 as 10 + 3 and 15 as 10 + 5.
- Multiply (10 + 3)(10 + 5) by the FOIL method.
- Multiply 13 • 15 without using a calculator.
- Which way is easier for you? Why?
- Mental math You can use binomial multiplication to multiply numbers without a calculator. Say you need to multiply 18 times 17. Think of 18 as 20 − 2 and 17 as 20 − 3.
- Multiply (20 − 2)(20 − 3) by the FOIL method.
- Multiply 18 • 17 without using a calculator.
- Which way is easier for you? Why?
Writing Exercises
- Which method do you prefer to use when multiplying two binomials—the Distributive Property, the FOIL method, or the Vertical Method? Why?
- Which method do you prefer to use when multiplying a trinomial by a binomial—the Distributive Property or the Vertical Method? Why?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
(b) What does this checklist tell you about your mastery of this section? What steps will you take to improve?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


