4.11: Add and Subtract Mixed Numbers (Part 2)
- Page ID
- 6066
Subtract Mixed Numbers with a Common Denominator
Now we will subtract mixed numbers without using a model. But it may help to picture the model in your mind as you read the steps.
Step 1. Rewrite the problem in vertical form.
Step 2. Compare the two fractions.
- If the top fraction is larger than the bottom fraction, go to Step 3.
- If not, in the top mixed number, take one whole and add it to the fraction part, making a mixed number with an improper fraction.
Step 3. Subtract the fractions.
Step 4. Subtract the whole numbers.
Step 5. Simplify, if possible.
Find the difference: \(5 \dfrac{3}{5} − 2 \dfrac{4}{5}\).
Solution
| Rewrite the problem in vertical form. | \(\begin{split} & 5 \dfrac{3}{5} \\ - & 2 \dfrac{4}{5} \\ \hline \end{split}\) |
| Since \(\dfrac{3}{5}\) is less than \(\dfrac{4}{5}\), take 1 from the 5 and add it to the \(\dfrac{3}{5}\): \(\left(\dfrac{5}{5} + \dfrac{3}{5} = \dfrac{8}{5}\right)\) | 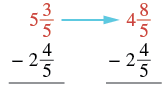 |
| Subtract the fractions. | \(\begin{split} & 4 \textcolor{red}{\dfrac{8}{5}} \\ - & 2 \textcolor{red}{\dfrac{4}{5}} \\ \hline \\ & \; \textcolor{red}{\dfrac{4}{5}} \end{split}\) |
| Subtract the whole parts. The result is in simplest form. | \(\begin{split} & \textcolor{red}{4} \dfrac{8}{5} \\ - & \textcolor{red}{2} \dfrac{4}{5} \\ \hline \\ & 2 \dfrac{4}{5} \end{split}\) |
Since the problem was given with mixed numbers, we leave the result as mixed numbers.
Find the difference: \(6 \dfrac{4}{9} − 3 \dfrac{7}{9}\).
- Answer
-
\(2\dfrac{2}{3}\)
Find the difference: \(4 \dfrac{4}{7} − 2 \dfrac{6}{7}\).
- Answer
-
\(1\dfrac{5}{7}\)
Just as we did with addition, we could subtract mixed numbers by converting them first to improper fractions. We should write the answer in the form it was given, so if we are given mixed numbers to subtract we will write the answer as a mixed number.
Step 1. Rewrite the mixed numbers as improper fractions.
Step 2. Subtract the numerators.
Step 3. Write the answer as a mixed number, simplifying the fraction part, if possible.
Find the difference by converting to improper fractions: \(9 \dfrac{6}{11} − 7 \dfrac{10}{11}\).
Solution
| Rewrite as improper fractions. | \(\dfrac{105}{11} - \dfrac{87}{11}\) |
| Subtract the numerators. | \(\dfrac{18}{11}\) |
| Rewrite as a mixed number. | \(1 \dfrac{7}{11}\) |
Find the difference by converting to improper fractions: \(6 \dfrac{4}{9} − 3 \dfrac{7}{9}\).
- Answer
-
\(2\dfrac{2}{3}\)
Find the difference by converting to improper fractions: \(4 \dfrac{4}{7} − 2 \dfrac{6}{7}\).
- Answer
-
\(1\dfrac{5}{7}\)
Add and Subtract Mixed Numbers with Different Denominators
To add or subtract mixed numbers with different denominators, we first convert the fractions to equivalent fractions with the LCD. Then we can follow all the steps we used above for adding or subtracting fractions with like denominators.
Add: \(2 \dfrac{1}{2} + 5 \dfrac{2}{3}\).
Solution
Since the denominators are different, we rewrite the fractions as equivalent fractions with the LCD, \(6\). Then we will add and simplify.
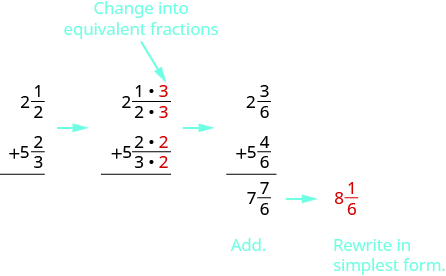
We write the answer as a mixed number because we were given mixed numbers in the problem.
Add: \(1 \dfrac{5}{6} + 4 \dfrac{3}{4}\).
- Answer
-
\(6\dfrac{7}{12}\)
Add: \(3 \dfrac{4}{5} + 8 \dfrac{1}{2}\).
- Answer
-
\(12\dfrac{3}{10}\)
Subtract: \(4 \dfrac{3}{4} − 2 \dfrac{7}{8}\).
Solution
Since the denominators of the fractions are different, we will rewrite them as equivalent fractions with the LCD \(8\). Once in that form, we will subtract. But we will need to borrow \(1\) first.
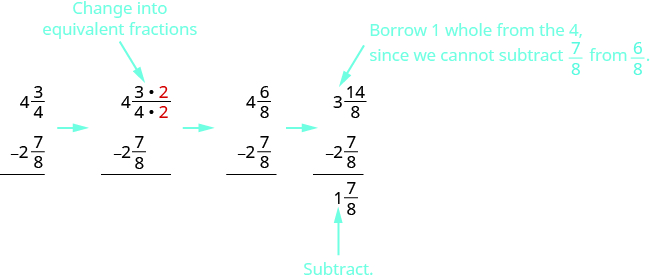
We were given mixed numbers, so we leave the answer as a mixed number.
Find the difference: \(8 \dfrac{1}{2} − 3 \dfrac{4}{5}\).
- Answer
-
\(4\dfrac{7}{10}\)
Find the difference: \(4 \dfrac{3}{4} − 1 \dfrac{5}{6}\).
- Answer
-
\(2\dfrac{11}{12}\)
Subtract: \(3 \dfrac{5}{11} − 4 \dfrac{3}{4}\).
Solution
We can see the answer will be negative since we are subtracting \(4\) from \(3\). Generally, when we know the answer will be negative it is easier to subtract with improper fractions rather than mixed numbers.
| Change to equivalent fractions with the LCD. |
\(3 \dfrac{5 \cdot 4}{11 \cdot 4} - 4 \dfrac{3 \cdot 11}{4 \cdot 11}\) \(3 \dfrac{20}{44} - 4 \dfrac{33}{44}\) |
| Rewrite as improper fractions. | \(\dfrac{152}{44} - \dfrac{209}{44}\) |
| Subtract. | \(- \dfrac{57}{44}\) |
| Rewrite as a mixed number. | \(- 1 \dfrac{13}{44}\) |
Subtract: \(1 \dfrac{3}{4} − 6 \dfrac{7}{8}\).
- Answer
-
\(-\dfrac{41}{8}\)
Subtract: \(10 \dfrac{3}{7} − 22 \dfrac{4}{9}\).
- Answer
-
\(-\dfrac{757}{63}\)
Access Additional Online Resources
- Adding Mixed Numbers
- Subtracting Mixed Numbers
Practice Makes Perfect
Model Addition of Mixed Numbers
In the following exercises, use a model to find the sum. Draw a picture to illustrate your model.
- \(1 \dfrac{1}{5} + 3 \dfrac{1}{5}\)
- \(2 \dfrac{1}{3} + 1 \dfrac{1}{3}\)
- \(1 \dfrac{3}{8} + 1 \dfrac{7}{8}\)
- \(1 \dfrac{5}{6} + 1 \dfrac{5}{6}\)
Add Mixed Numbers with a Common Denominator
In the following exercises, add.
- \(5 \dfrac{1}{3} + 6 \dfrac{1}{3}\)
- \(2 \dfrac{4}{9} + 5 \dfrac{1}{9}\)
- \(4 \dfrac{5}{8} + 9 \dfrac{3}{8}\)
- \(7 \dfrac{9}{10} + 3 \dfrac{1}{10}\)
- \(3 \dfrac{4}{5} + 6 \dfrac{4}{5}\)
- \(9 \dfrac{2}{3} + 1 \dfrac{2}{3}\)
- \(6 \dfrac{9}{10} + 8 \dfrac{3}{10}\)
- \(8 \dfrac{4}{9} + 2 \dfrac{8}{9}\)
Model Subtraction of Mixed Numbers
In the following exercises, use a model to find the difference. Draw a picture to illustrate your model.
- \(1 \dfrac{1}{6} - \dfrac{1}{6}\)
- \(1 \dfrac{1}{8} - \dfrac{1}{8}\)
Subtract Mixed Numbers with a Common Denominator
In the following exercises, find the difference.
- \(2 \dfrac{7}{8} - 1 \dfrac{3}{8}\)
- \(2 \dfrac{7}{12} - 1 \dfrac{5}{12}\)
- \(8 \dfrac{3}{7} - 4 \dfrac{4}{7}\)
- \(19 \dfrac{13}{15} - 13 \dfrac{7}{15}\)
- \(8 \dfrac{3}{7} - 4 \dfrac{4}{7}\)
- \(5 \dfrac{2}{9} - 3 \dfrac{4}{9}\)
- \(2 \dfrac{5}{8} - 1 \dfrac{7}{8}\)
- \(2 \dfrac{5}{12} - 1 \dfrac{7}{12}\)
Add and Subtract Mixed Numbers with Different Denominators
In the following exercises, write the sum or difference as a mixed number in simplified form.
- \(3 \dfrac{1}{4} + 6 \dfrac{1}{3}\)
- \(2 \dfrac{1}{6} + 5 \dfrac{3}{4}\)
- \(1 \dfrac{5}{8} + 4 \dfrac{1}{2}\)
- \(7 \dfrac{2}{3} + 8 \dfrac{1}{2}\)
- \(2 \dfrac{5}{12} - 1 \dfrac{7}{12}\)
- \(6 \dfrac{4}{5} - 1 \dfrac{1}{4}\)
- \(2 \dfrac{2}{3} - 3 \dfrac{1}{2}\)
- \(2 \dfrac{7}{8} - 4 \dfrac{1}{3}\)
Mixed Practice
In the following exercises, perform the indicated operation and write the result as a mixed number in simplified form.
- \(2 \dfrac{5}{8} \cdot 1 \dfrac{3}{4}\)
- \(1 \dfrac{2}{3} \cdot 4 \dfrac{1}{6}\)
- \(\dfrac{2}{7} + \dfrac{4}{7}\)
- \(\dfrac{2}{9} + \dfrac{5}{9}\)
- \(1 \dfrac{5}{12} \div \dfrac{1}{12}\)
- \(2 \dfrac{3}{10} \div \dfrac{1}{10}\)
- \(13 \dfrac{5}{12} - 9 \dfrac{7}{12}\)
- \(15 \dfrac{5}{8} - 6 \dfrac{7}{8}\)
- \(\dfrac{5}{9} - \dfrac{4}{9}\)
- \(\dfrac{11}{15} - \dfrac{7}{15}\)
- 4 − \(\dfrac{3}{4}\)
- 6 − \(\dfrac{2}{5}\)
- \(\dfrac{9}{20} \div \dfrac{3}{4}\)
- \(\dfrac{7}{24} \div \dfrac{14}{3}\)
- \(9 \dfrac{6}{11} + 7 \dfrac{10}{11}\)
- \(8 \dfrac{5}{13} + 4 \dfrac{9}{13}\)
- \(3 \dfrac{2}{5} + 5 \dfrac{3}{4}\)
- \(2 \dfrac{5}{6} + 4 \dfrac{1}{5}\)
- \(\dfrac{8}{15} \cdot \dfrac{10}{19}\)
- \(\dfrac{5}{12} \cdot \dfrac{8}{9}\)
- \(6 \dfrac{7}{8} - 2 \dfrac{1}{3}\)
- \(6 \dfrac{5}{9} - 4 \dfrac{2}{5}\)
- \(5 \dfrac{2}{9} - 4 \dfrac{4}{5}\)
- \(4 \dfrac{3}{8} - 3 \dfrac{2}{3}\)
Everyday Math
- Sewing Renata is sewing matching shirts for her husband and son. According to the patterns she will use, she needs \(2 \dfrac{3}{8}\) yards of fabric for her husband’s shirt and \(1 \dfrac{1}{8}\) yards of fabric for her son’s shirt. How much fabric does she need to make both shirts?
- Sewing Pauline has \(3 \dfrac{1}{4}\) yards of fabric to make a jacket. The jacket uses \(2 \dfrac{2}{3}\) yards. How much fabric will she have left after making the jacket?
- Printing Nishant is printing invitations on his computer. The paper is \(8 \dfrac{1}{2}\) inches wide, and he sets the print area to have a \(1 \dfrac{1}{2}\)-inch border on each side. How wide is the print area on the sheet of paper?
- Framing a picture Tessa bought a picture frame for her son’s graduation picture. The picture is 8 inches wide. The picture frame is \(2 \dfrac{5}{8}\) inches wide on each side. How wide will the framed picture be?
Writing Exercises
- Draw a diagram and use it to explain how to add \(1 \dfrac{5}{8} + 2 \dfrac{7}{8}\).
- Edgar will have to pay $3.75 in tolls to drive to the city.
- Explain how he can make change from a $10 bill before he leaves so that he has the exact amount he needs.
- How is Edgar’s situation similar to how you subtract 10 − \(3 \dfrac{3}{4}\)?
- Add \(4 \dfrac{5}{12} + 3 \dfrac{7}{8}\) twice, first by leaving them as mixed numbers and then by rewriting as improper fractions. Which method do you prefer, and why?
- Subtract \(3 \dfrac{7}{8} − 4 \dfrac{5}{12}\) twice, first by leaving them as mixed numbers and then by rewriting as improper fractions. Which method do you prefer, and why?
Self Check
(a) After completing the exercises, use this checklist to evaluate your mastery of the objectives of this section.
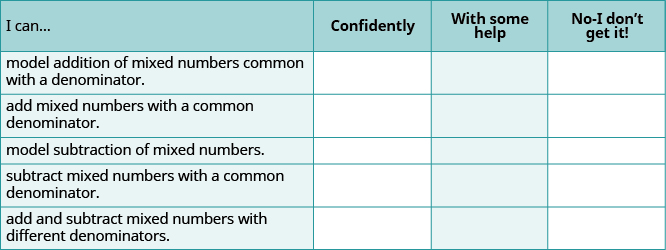
(b) After reviewing this checklist, what will you do to become confident for all objectives?
Contributors and Attributions
Lynn Marecek (Santa Ana College) and MaryAnne Anthony-Smith (Formerly of Santa Ana College). This content is licensed under Creative Commons Attribution License v4.0 "Download for free at http://cnx.org/contents/fd53eae1-fa2...49835c3c@5.191."


