8.3: Integral and Comparison Tests
- Page ID
- 4201
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Knowing whether or not a series converges is very important, especially when we discusses Power Series. Theorems 60 and 61 give criteria for when Geometric and \(p\)-series converge, and Theorem 63 gives a quick test to determine if a series diverges. There are many important series whose convergence cannot be determined by these theorems, though, so we introduce a set of tests that allow us to handle a broad range of series. We start with the Integral Test.
Integral Test
We stated in Section 8.1 that a sequence \(\{a_n\}\) is a function \(a(n)\) whose domain is \(\mathbb{N}\), the set of natural numbers. If we can extend \(a(n)\) to \(\mathbb{R}\), the real numbers, and it is both positive and decreasing on \([1,\infty)\), then the convergence of \( \sum\limits_{n=1}^\infty a_n\) is the same as \(\int\limits_1^\infty a(x)dx\).
theorem \(\PageIndex{1}\): integral test
Let a sequence \(\{a_n\}\) be defined by \(a_n=a(n)\), where \(a(n)\) is continuous, positive and decreasing on \([1,\infty)\). Then \( \sum\limits_{n=1}^\infty a_n\) converges, if, and only if, \(\int\limits_1^\infty a(x) dx\) converges.
We can demonstrate the truth of the Integral Test with two simple graphs. In Figure \(\PageIndex{1a}\), the height of each rectangle is \(a(n)=a_n\) for \(n=1,2,\ldots\), and clearly the rectangles enclose more area than the area under \(y=a(x)\). Therefore we can conclude that
\[\int\limits_1^\infty a(x) dx < \sum\limits_{n=1}^\infty a_n.\label{eq:integral_testa}\]
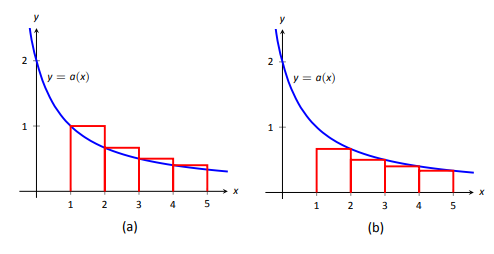
In Figure \(\PageIndex{1b}\), we draw rectangles under \(y=a(x)\) with the Right-Hand rule, starting with \(n=2\). This time, the area of the rectangles is less than the area under \(y=a(x)\), so \(\sum\limits_{n=2}^\infty a_n < \int\limits_1^\infty a(x) dx\). Note how this summation starts with \(n=2\); adding \(a_1\) to both sides lets us rewrite the summation starting with \(n=1\):
\[\sum\limits_{n=1}^\infty a_n < a_1 +\int\limits_1^\infty a(x) dx.\label{eq:integral_testb}\]
Combining Equations \ref{eq:integral_testa} and \ref{eq:integral_testb}, we have
\[\sum\limits_{n=1}^\infty a_n< a_1 +\int\limits_1^\infty a(x) dx < a_1 + \sum\limits_{n=1}^\infty a_n.\label{eq:integral_testc}\]
Theorem \(\PageIndex{1}\)
From Equation \ref{eq:integral_testc} we can make the following two statements:
- If \( \sum\limits_{n=1}^\infty a_n\) diverges, so does \(\int\limits_1^\infty a(x) dx\) (because \( \sum\limits_{n=1}^\infty a_n < a_1 +\int\limits_1^\infty a(x) dx)\)
- If \( \sum\limits_{n=1}^\infty a_n\) converges, so does \(\int\limits_1^\infty a(x) dx\) (because \( \int\limits_1^\infty a(x) dx < \sum\limits_{n=1}^\infty a_n.)\)
Therefore the series and integral either both converge or both diverge.
Theorem\(\PageIndex{1}\) allows us to extend this theorem to series where \(a(n)\) is positive and decreasing on \([b,\infty)\) for some \(b>1\).
Example \(\PageIndex{1}\): Using the Integral Test
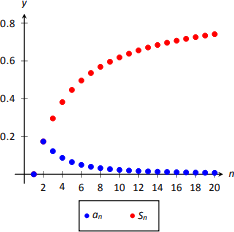
Determine the convergence of \(\sum\limits_{n=1}^\infty \dfrac{\ln n}{n^2}\). (The terms of the sequence \(\{a_n\} = \{\ln n/n^2\}\) and the n\(^{\text{th}}\) partial sums are given in Figure \(\PageIndex{2}\)).
Solution
Figure \(\PageIndex{2}\) implies that \(a(n) = (\ln n)/n^2\) is positive and decreasing on \([2,\infty)\). We can determine this analytically, too. We know \(a(n)\) is positive as both \(\ln n\) and \(n^2\) are positive on \([2,\infty)\). To determine that \(a(n)\) is decreasing, consider \(a^\prime(n) = (1-2\ln n)/n^3\), which is negative for \(n\geq 2\). Since \(a^\prime(n)\) is negative, \(a(n)\) is decreasing.
Applying the Integral Test, we test the convergence of \( \int\limits_1^\infty \dfrac{\ln x}{x^2} dx\). Integrating this improper integral requires the use of Integration by Parts, with \(u = \ln x\) and \(dv = 1/x^2 dx\).
\[\begin{align*}\int\limits_1^\infty \dfrac{\ln x}{x^2} dx &=\lim\limits_{b\to\infty} \int\limits_1^b \dfrac{\ln x}{x^2} dx\\ &=\lim\limits_{b\to\infty} -\dfrac1x\ln x\Big|_1^b + \int\limits_1^b\dfrac1{x^2} dx \\ &=\lim\limits_{b\to\infty} -\dfrac1x\ln x -\dfrac 1x\Big|_1^b\\ &=\lim\limits_{b\to\infty}1-\dfrac1b-\dfrac{\ln b}{b}.\quad \text{Apply L'H\(\hat o\)pital's Rule:}\\ &= 1. \end{align*}\]
Since \( \int\limits_1^\infty \dfrac{\ln x}{x^2} dx\) converges, so does \( \sum\limits_{n=1}^\infty \dfrac{\ln n}{n^2}\).
Theorem 61 was given without justification, stating that the general \(p\)-series \( \sum\limits_{n=1}^\infty \dfrac 1{(an+b)^p}\) converges if, and only if, \(p>1\). In the following example, we prove this to be true by applying the Integral Test.
Example \(\PageIndex{2}\): Using the Integral Test to establish Theorem 61
Use the Integral Test to prove that \( \sum\limits_{n=1}^\infty \dfrac1{(an+b)^p}\) converges if, and only if, \(p>1\).
Solution
Consider the integral \(\int\limits_1^\infty \dfrac1{(ax+b)^p} dx\); assuming \(p\neq 1\),
\[\begin{align*}
\int\limits_1^\infty \dfrac1{(ax+b)^p} dx &=\lim\limits_{c\to\infty} \int\limits_1^c \dfrac1{(ax+b)^p} dx \\
&=\lim\limits_{c\to\infty} \dfrac{1}{a(1-p)}(ax+b)^{1-p}\Big|_1^c\\
&=\lim\limits_{c\to\infty} \dfrac{1}{a(1-p)}\big((ac+b)^{1-p}-(a+b)^{1-p}\big).
\end{align*}\]
This limit converges if, and only if, \(p>1\). It is easy to show that the integral also diverges in the case of \(p=1\). (This result is similar to the work preceding Key Idea 21.)
Therefore \( \sum\limits_{n=1}^\infty \dfrac 1{(an+b)^p}\) converges if, and only if, \(p>1\).
We consider two more convergence tests in this section, both comparison tests. That is, we determine the convergence of one series by comparing it to another series with known convergence.
Direct Comparison Test
theorem \(\PageIndex{1}\): direct comparison test
Let \(\{a_n\}\) and \(\{b_n\}\) be positive sequences where \(a_n\leq b_n\) for all \(n\geq N\), for some \(N\geq 1\).
- If \( \sum\limits_{n=1}^\infty b_n\) converges, then \( \sum\limits_{n=1}^\infty a_n\) converges.
- If \( \sum\limits_{n=1}^\infty a_n\) diverges, then \( \sum\limits_{n=1}^\infty b_n\) diverges.
Note: A sequence \(\{a_n\}\) is a positive sequence if \(a_n>0\) for all \(n\).
Because of Theorem 64, any theorem that relies on a positive sequence still holds true when \(a_n>0\) for all but a finite number of values of \(n\).
Example \(\PageIndex{3}\): Applying the Direct Comparison Test
Determine the convergence of \(\sum\limits_{n=1}^\infty \dfrac1{3^n+n^2}\).
Solution
This series is neither a geometric or \(p\)-series, but seems related. We predict it will converge, so we look for a series with larger terms that converges. (Note too that the Integral Test seems difficult to apply here.)
Since \(3^n < 3^n+n^2\), \( \dfrac1{3^n}> \dfrac1{3^n+n^2}\) for all \(n\geq1\). The series \(\sum\limits_{n=1}^\infty \dfrac{1}{3^n}\) is a convergent geometric series; by Theorem 66, \( \sum\limits_{n=1}^\infty \dfrac1{3^n+n^2}\) converges.
Example \(\PageIndex{4}\): Applying the Direct Comparison Test
Determine the convergence of \(\sum\limits_{n=1}^\infty \dfrac{1}{n-\ln n}\).
Solution
We know the Harmonic Series \(\sum\limits_{n=1}^\infty \dfrac1n\) diverges, and it seems that the given series is closely related to it, hence we predict it will diverge.
Since \(n\geq n-\ln n\) for all \(n\geq 1\), \( \dfrac1n \leq \dfrac1{n-\ln n}\) for all \(n\geq 1\).
The Harmonic Series diverges, so we conclude that \(\sum\limits_{n=1}^\infty \dfrac{1}{n-\ln n}\) diverges as well.
The concept of direct comparison is powerful and often relatively easy to apply. Practice helps one develop the necessary intuition to quickly pick a proper series with which to compare. However, it is easy to construct a series for which it is difficult to apply the Direct Comparison Test.
Consider \(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\). It is very similar to the divergent series given in Example 8.3.5. We suspect that it also diverges, as \( \dfrac 1n \approx \dfrac1{n+\ln n}\) for large \(n\). However, the inequality that we naturally want to use "goes the wrong way'': since \(n\leq n+\ln n\) for all \(n\geq 1\), \(\dfrac1n \geq \dfrac{1}{n+\ln n}\) for all \(n\geq 1\). The given series has terms less than the terms of a divergent series, and we cannot conclude anything from this.
Fortunately, we can apply another test to the given series to determine its convergence.
Large Limit Comparison Test
Theorem 67: limit comparison test
Let \(\{a_n\}\) and \(\{b_n\}\) be positive sequences.
- If \(\lim_{n\to\infty} \dfrac{a_n}{b_n} = L\), where \(L\) is a positive real number, then \( \sum\limits_{n=1}^\infty a_n\) and \( \sum\limits_{n=1}^\infty b_n\) either both converge or both diverge.
- If \(\lim_{n\to\infty} \dfrac{a_n}{b_n} = 0\), then if \( \sum\limits_{n=1}^\infty b_n\) converges, then so does \( \sum\limits_{n=1}^\infty a_n\).
- If \(\lim_{n\to\infty} \dfrac{a_n}{b_n} = \infty\), then if \( \sum\limits_{n=1}^\infty b_n\) diverges, then so does \( \sum\limits_{n=1}^\infty a_n\).
Theorem 67 is most useful when the convergence of the series from \(\{b_n\}\) is known and we are trying to determine the convergence of the series from \(\{a_n\}\).
We use the Limit Comparison Test in the next example to examine the series \(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) which motivated this new test.
Example \(\PageIndex{5}\): Applying the Limit Comparison Test
Determine the convergence of \(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) using the Limit Comparison Test.
Solution
We compare the terms of \(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) to the terms of the Harmonic Sequence \(\sum\limits_{n=1}^\infty \dfrac1{n}\):
\[\begin{align*}
\lim_{n\to\infty}\dfrac{1/(n+\ln n)}{1/n} &=\lim\limits_{n\to\infty} \dfrac{n}{n+\ln n} \\
&= 1\quad \text{(after applying L'H\(\hat o\)pital's Rule)}.
\end{align*}\]
Since the Harmonic Series diverges, we conclude that \(\sum\limits_{n=1}^\infty \dfrac1{n+\ln n}\) diverges as well.
Example \(\PageIndex{6}\): Applying the Limit Comparison Test
Determine the convergence of \(\sum\limits_{n=1}^\infty \dfrac1{3^n-n^2}\)
Solution
This series is similar to the one in Example 8.3.3, but now we are considering "\(3^n-n^2\)'' instead of "\(3^n+n^2\).'' This difference makes applying the Direct Comparison Test difficult.
Instead, we use the Limit Comparison Test and compare with the series \(\sum\limits_{n=1}^\infty \dfrac1{3^n}\):
\[\begin{align*}
\lim_{n\to\infty}\dfrac{1/(3^n-n^2)}{1/3^n} &=\lim\limits_{n\to\infty}\dfrac{3^n}{3^n-n^2} \\
&= 1 \quad \text{(after applying L'H\(\hat o\)pital's Rule twice)}.
\end{align*}\]
We know \(\sum\limits_{n=1}^\infty \dfrac1{3^n}\) is a convergent geometric series, hence \(\sum\limits_{n=1}^\infty \dfrac1{3^n-n^2}\) converges as well.
As mentioned before, practice helps one develop the intuition to quickly choose a series with which to compare. A general rule of thumb is to pick a series based on the dominant term in the expression of \(\{a_n\}\). It is also helpful to note that factorials dominate exponentials, which dominate algebraic functions (e.g., polynomials), which dominate logarithms. In the previous example, the dominant term of \(\dfrac{1}{3^n-n^2}\) was \(3^n\), so we compared the series to \( \sum\limits_{n=1}^\infty \dfrac1{3^n}\). It is hard to apply the Limit Comparison Test to series containing factorials, though, as we have not learned how to apply L'H\(\hat o\)pital's Rule to \(n!\).
Example \(\PageIndex{7}\): Applying the Limit Comparison Test
Determine the convergence of \(\sum\limits_{n=1}^\infty \dfrac{\sqrt{n}+3}{n^2-n+1}\).
Solution
We naively attempt to apply the rule of thumb given above and note that the dominant term in the expression of the series is \(1/n^2\). Knowing that \( \sum\limits_{n=1}^\infty \dfrac1{n^2}\) converges, we attempt to apply the Limit Comparison Test:
\[\begin{align*}
\lim_{n\to\infty}\dfrac{(\sqrt{n}+3)/(n^2-n+1)}{1/n^2} &=\lim\limits_{n\to\infty}\dfrac{n^2(\sqrt n+3)}{n^2-n+1}\\
&= \infty \quad \text{(Apply L'H\(\hat o\)pital's Rule)}.
\end{align*}\]
Theorem 67 part (3) only applies when \(\sum\limits_{n=1}^\infty b_n\) diverges; in our case, it converges. Ultimately, our test has not revealed anything about the convergence of our series.
The problem is that we chose a poor series with which to compare. Since the numerator and denominator of the terms of the series are both algebraic functions, we should have compared our series to the dominant term of the numerator divided by the dominant term of the denominator.
The dominant term of the numerator is \(n^{1/2}\) and the dominant term of the denominator is \(n^2\). Thus we should compare the terms of the given series to \(n^{1/2}/n^2 = 1/n^{3/2}\):
\[\begin{align*}
\lim_{n\to\infty}\dfrac{(\sqrt{n}+3)/(n^2-n+1)}{1/n^{3/2}} &=\lim\limits_{n\to \infty} \dfrac{n^{3/2}(\sqrt n+3)}{n^2-n+1} \\
&= 1\quad \text{(Apply L'H\(\hat o\)pital's Rule)}.
\end{align*}\]
Since the \(p\)-series \(\sum\limits_{n=1}^\infty \dfrac1{n^{3/2}}\) converges, we conclude that \(\sum\limits_{n=1}^\infty \dfrac{\sqrt{n}+3}{n^2-n+1}\) converges as well.
We mentioned earlier that the Integral Test did not work well with series containing factorial terms. The next section introduces the Ratio Test, which does handle such series well. We also introduce the Root Test, which is good for series where each term is raised to a power.
Contributors and Attributions
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/


