6.1: Substitution
- Page ID
- 4185
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The previous chapter introduced the antiderivative and connected it to signed areas under a curve through the Fundamental Theorem of Calculus. The next chapter explores more applications of definite integrals than just area. As evaluating definite integrals will become important, we will want to find antiderivatives of a variety of functions.
This chapter is devoted to exploring techniques of antidifferentiation. While not every function has an antiderivative in terms of elementary functions (a concept introduced in the section on Numerical Integration), we can still find antiderivatives of a wide variety of functions.
Substitution
We motivate this section with an example. Let \(f(x) = (x^2+3x-5)^{10}\). We can compute \(f'(x)\) using the Chain Rule. It is:
\[f'(x) = 10(x^2+3x-5)^9\cdot(2x+3) = (20x+30)(x^2+3x-5)^9.\]
Now consider this: What is \(\int (20x+30)(x^2+3x-5)^9\ dx\)? We have the answer in front of us;
\[\int (20x+30)(x^2+3x-5)^9\ dx = (x^2+3x-5)^{10}+C.\]
How would we have evaluated this indefinite integral without starting with \(f(x)\) as we did?
This section explores integration by substitution. It allows us to "undo the Chain Rule." Substitution allows us to evaluate the above integral without knowing the original function first.
The underlying principle is to rewrite a "complicated" integral of the form \(\int f(x)\ dx\) as a not--so--complicated integral \(\int h(u)\ du\). We'll formally establish later how this is done. First, consider again our introductory indefinite integral, \(\int (20x+30)(x^2+3x-5)^9\ dx\). Arguably the most "complicated" part of the integrand is \((x^2+3x-5)^9\). We wish to make this simpler; we do so through a substitution. Let \(u=x^2+3x-5\). Thus
\[(x^2+3x-5)^9 = u^9.\]
We have established \(u\) as a function of \(x\), so now consider the differential of \(u\):
\[du = (2x+3)dx.\]
Keep in mind that \((2x+3)\) and \(dx\) are multiplied; the \(dx\) is not "just sitting there."
Return to the original integral and do some substitutions through algebra:
\[\begin{align} \int (20x+30)(x^2+3x-5)^9\ dx &= \int 10(2x+3)(x^2+3x-5)^9\ dx \\ &=\int 10(\underbrace{x^2+3x-5}_u)^9\underbrace{(2x+3)\ dx}_{du} \\ &=\int 10u^9\ du \\ &= u^{10} + C \quad \text{(replace \(u\) with \(x^2+3x-5\))}\\ &= (x^2+3x-5)^{10} +C\end{align}\]
One might well look at this and think "I (sort of) followed how that worked, but I could never come up with that on my own," but the process is learnable. This section contains numerous examples through which the reader will gain understanding and mathematical maturity enabling them to regard substitution as a natural tool when evaluating integrals.
We stated before that integration by substitution "undoes" the Chain Rule. Specifically, let \(F(x)\) and \(g(x)\) be differentiable functions and consider the derivative of their composition:
\[\frac{d}{dx}\Big(F\big(g(x)\big)\Big) = F'(g(x))g'(x).\]
Thus
\[\int F'(g(x))g'(x)\ dx = F(g(x)) + C.\]
Integration by substitution works by recognizing the "inside" function \(g(x)\) and replacing it with a variable. By setting \(u=g(x)\), we can rewrite the derivative as
\[\frac{d}{dx}\Big(F\big(u\big)\Big) = F'(u)u'.\]
Since \(du = g'(x)dx\), we can rewrite the above integral as
\[\int F'(g(x))g'(x)\ dx = \int F'(u) du = F(u)+C = F(g(x))+ C.\]
This concept is important so we restate it in the context of a theorem.
Theorem \(\PageIndex{1}\): Integration by Substitution
Let \(F\) and \(g\) be differentiable functions, where the range of \(g\) is an interval \(I\) contained in the domain of \(F\). Then
\[\int F'(g(x))g'(x)\ dx = F(g(x)) + C.\]
If \(u = g(x)\), then \(du = g'(x)dx\) and
\[\int F'(g(x))g'(x)\ dx = \int F'(u)\ du = F(u)+C = F(g(x))+C.\]
The point of substitution is to make the integration step easy. Indeed, the step \(\int F'(u)\ du = F(u) + C\) looks easy, as the antiderivative of the derivative of \(F\) is just \(F\), plus a constant. The "work" involved is making the proper substitution. There is not a step-by-step process that one can memorize; rather, experience will be one's guide. To gain experience, we now embark on many examples.
Example \(\PageIndex{1}\): Integrating by substitution
Evaluate \(\int x\sin(x^2+5)\ dx\).
Solution
Knowing that substitution is related to the Chain Rule, we choose to let \(u\) be the "inside" function of \(\sin(x^2+5)\). (This is not always a good choice, but it is often the best place to start.)
Let \(u = x^2+5\), hence \(du = 2x\,dx\). The integrand has an \(x\,dx\) term, but not a \(2x\,dx\) term. (Recall that multiplication is commutative, so the \(x\) does not physically have to be next to \(dx\) for there to be an \(x\,dx\) term.) We can divide both sides of the \(du\) expression by 2:
\[du = 2x\,dx \quad \Rightarrow \quad \frac12du = x\,dx.\]
We can now substitute.
\[\begin{align}\int x\sin(x^2+5)\ dx &= \int \sin(\underbrace{x^2+5}_u) \underbrace{x\ dx}_{\frac12du}\\ &= \int \frac12\sin u\ du\end{align}\]
\[\begin{align} \phantom{\int x\sin(x^2+5)\ dx} &= -\frac12\cos u + C \quad \text{ (now replace \(u\) with \(x^2+5\))}\\ &=-\frac12\cos(x^2+5) + C. \end{align}\]
Thus \(\int x\sin(x^2+5)\ dx = -\frac12\cos(x^2+5)+C\). We can check our work by evaluating the derivative of the right hand side.
Example \(\PageIndex{2}\): Integrating by substitution
Evaluate \(\int \cos(5x)\ dx\).
Solution
Again let \(u\) replace the "inside" function. Letting \(u = 5x\), we have \(du = 5dx\). Since our integrand does not have a \(5dx\) term, we can divide the previous equation by \(5\) to obtain \(\frac15du = dx\). We can now substitute.
\[\begin{align} \int \cos(5x)\ dx &= \int \cos(\underbrace{5x}_u) \underbrace{dx}_{\frac15du} \\&= \int \frac15\cos u \ du \\ &= \frac15\sin u + C \\&= \frac15\sin (5x)+C. \end{align}\]
We can again check our work through differentiation.
The previous example exhibited a common, and simple, type of substitution. The "inside" function was a linear function (in this case, \(y = 5x\)). When the inside function is linear, the resulting integration is very predictable, outlined here.
Key Idea 10: Substitution With A Linear Function
Consider \(\int F'(ax+b)\ dx\), where \(a\neq 0\) and \(b\) are constants. Letting \(u = ax+b\) gives \(du = a\cdot dx\), leading to the result
\[\int F'(ax+b)\ dx = \frac{1}{a}F(ax+b) + C.\]
Thus \(\int \sin (7x-4)\ dx = -\frac17\cos(7x-4)+C\). Our next example can use Key Idea 10, but we will only employ it after going through all of the steps.
Example \(\PageIndex{3}\): Integrating by substituting a linear function
Evaluate \(\int \frac{7}{-3x+1}\ dx\).
Solution
View this a composition of functions \(f(g(x))\), where \(f(x) = 7/x\) and \(g(x) = -3x+1\). Employing our understanding of substitution, we let \(u = -3x+1\), the inside function. Thus \(du = -3dx\). The integrand lacks a \(-3\); hence divide the previous equation by \(-3\) to obtain \(-du/3 = dx\). We can now evaluate the integral through substitution.
\[\begin{align} \int \frac{7}{-3x+1}\ dx &= \int \frac{7}{u}\frac{du}{-3} \\ &= \frac{-7}3\int \frac{du}{u} \\ &= \frac{-7}3\ln |u| + C\\ &=-\frac73\ln|-3x+1| + C. \end{align}\]
Using Key Idea 10 is faster, recognizing that \(u\) is linear and \(a = -3\). One may want to continue writing out all the steps until they are comfortable with this particular shortcut.
Not all integrals that benefit from substitution have a clear "inside" function. Several of the following examples will demonstrate ways in which this occurs.
Example \(\PageIndex{4}\): Integrating by substitution
Evaluate \(\int \sin x\cos x\ dx\).
Solution
There is not a composition of function here to exploit; rather, just a product of functions. Do not be afraid to experiment; when given an integral to evaluate, it is often beneficial to think "If I let \(u\) be this, then \(du\) must be that ..." and see if this helps simplify the integral at all.
In this example, let's set \(u = \sin x\). Then \(du = \cos x\ dx\), which we have as part of the integrand! The substitution becomes very straightforward:
\[ \begin{align} \int \sin x\cos x\ dx &= \int u\ du \\ &= \frac12u^2+ C \\ &= \frac12\sin^2 x + C. \end{align}\]
One would do well to ask "What would happen if we let \(u = \cos x\)?" The result is just as easy to find, yet looks very different. The challenge to the reader is to evaluate the integral letting \(u = \cos x\) and discover why the answer is the same, yet looks different.
Our examples so far have required "basic substitution." The next example demonstrates how substitutions can be made that often strike the new learner as being "nonstandard."
Example \(\PageIndex{5}\): Integrating by substitution
Evaluate \(\int x\sqrt{x+3}\ dx\).
Solution
Recognizing the composition of functions, set \(u = x+3\). Then \(du = dx\), giving what seems initially to be a simple substitution. But at this stage, we have:
\[\int x\sqrt{x+3}\ dx = \int x\sqrt{u}\ du.\]
We cannot evaluate an integral that has both an \(x\) and an \(u\) in it. We need to convert the \(x\) to an expression involving just \(u\).
Since we set \(u = x+3\), we can also state that \(u-3 = x\). Thus we can replace \(x\) in the integrand with \(u-3\). It will also be helpful to rewrite \(\sqrt{u}\) as \(u^\frac12\).
\[\begin{align} \int x\sqrt{x+3} \ dx &= \int (u-3)u^\frac12\ du \\ &= \int \big(u^\frac32 - 3u^\frac12\big) \ du \\ &= \frac25u^\frac52 - 2u^\frac32 + C \\ &= \frac25(x+3)^\frac52 - 2(x+3)^\frac32 + C.\end{align}\]
Checking your work is always a good idea. In this particular case, some algebra will be needed to make one's answer match the integrand in the original problem.
Example \(\PageIndex{6}\): Integrating by substitution
Evaluate \(\int \frac{1}{x\ln x}\ dx\).
Solution
This is another example where there does not seem to be an obvious composition of functions. The line of thinking used in Example \(\PageIndex{5}\) is useful here: choose something for \(u\) and consider what this implies \(du\) must be. If \(u\) can be chosen such that \(du\) also appears in the integrand, then we have chosen well.
Choosing \(u = 1/x\) makes \(du = -1/x^2\ dx\); that does not seem helpful. However, setting \(u = \ln x\) makes \(du = 1/x\ dx\), which is part of the integrand. Thus:
\[\begin{align} \int \frac1{x\ln x}\ dx &= \int \frac{1}{\underbrace{\ln x}_{1/u}}\underbrace{\frac1x\ dx}_{du} \\ &= \int \frac1u\ du \\ &= \ln |u| + C \\ &= \ln | \ln x| + C.\end{align}\]
The final answer is interesting; the natural log of the natural log. Take the derivative to confirm this answer is indeed correct.
Integrals Involving Trigonometric Functions
Section 6.3 delves deeper into integrals of a variety of trigonometric functions; here we use substitution to establish a foundation that we will build upon.
The next three examples will help fill in some missing pieces of our antiderivative knowledge. We know the antiderivatives of the sine and cosine functions; what about the other standard functions tangent, cotangent, secant and cosecant? We discover these next.
Example \(\PageIndex{7}\): Integration by substitution: antiderivatives of \(\tan x\)
Evaluate \(\int \tan x\ dx.\)
Solution
The previous paragraph established that we did not know the antiderivatives of tangent, hence we must assume that we have learned something in this section that can help us evaluate this indefinite integral.
Rewrite \(\tan x\) as \(\sin x/\cos x\). While the presence of a composition of functions may not be immediately obvious, recognize that \(\cos x\) is "inside" the \(1/x\) function. Therefore, we see if setting \(u = \cos x\) returns usable results. We have that \(du = -\sin x\ dx\), hence \(-du = \sin x\ dx\). We can integrate:
\[\begin{align}\int \tan x \ dx &= \int \frac{\sin x}{\cos x}\ dx \\ &= \int \frac1{\underbrace{\cos x}_u}\underbrace{\sin x\ dx}_{-du} \\ &= \int \frac {-1}u \ du\\ &= -\ln |u| + C \\ &= -\ln |\cos x| + C.\end{align}\]
Some texts prefer to bring the \(-1\) inside the logarithm as a power of \(\cos x\), as in:
\[\begin{align} -\ln |\cos x| + C &= \ln |(\cos x)^{-1}| + C\\ &= \ln \left| \frac{1}{\cos x}\right| + C\\&= \ln |\sec x| + C.\end{align}\]
Thus the result they give is \(\int \tan x \ dx = \ln|\sec x| + C\). These two answers are equivalent.
Example \(\PageIndex{8}\): Integrating by substitution: antiderivatives of \(\sec x\)
Evaluate \(\int \sec x\ dx\).
Solution
This example employs a wonderful trick: multiply the integrand by "1" so that we see how to integrate more clearly. In this case, we write "1" as
\[1 = \frac{\sec x + \tan x}{\sec x + \tan x}.\]
This may seem like it came out of left field, but it works beautifully. Consider:
\[\begin{align} \int \sec x\ dx &= \int \sec x\cdot \frac{\sec x + \tan x}{\sec x + \tan x}\ dx \\ &= \int \frac{\sec^2 x + \sec x\tan x}{\sec x + \tan x}\ dx.\end{align}\]
Now let \(u = \sec x+\tan x\); this means \(du = (\sec x\tan x+ \sec^2 x)\ dx\), which is our numerator. Thus:
\[\begin{align} &= \int \frac{du}{u} \\ &= \ln |u| + C \\ &= \ln |\sec x+\tan x| + C.\end{align}\]
We can use similar techniques to those used in Examples \(\PageIndex{6}\) and \(\PageIndex{7}\) to find antiderivatives of \(\cot x\) and \(\csc x\) (which the reader can explore in the exercises.) We summarize our results here.
Theorem \(\PageIndex{1}\): Antiderivatives of Trigonometric Functions
- \( \int \sin x \ dx = -\cos x +C\)
- \(\int \cos x\ dx = \sin x + C\)
- \(\int \tan x\ dx = -\ln|\cos x|+C\)
- \( \int \csc x \ dx = -\ln|\csc x+\cot x| +C\)
- \(\int \sec x\ dx = \ln|\sec x+\tan x| + C\)
- \( \int \cot x\ dx = \ln|\sin x|+C\)
We explore one more common trigonometric integral.
Example \(\PageIndex{9}\): Integration by substitution: powers of \(\cos x\) and \(\sin x\)
Evaluate \(\int \cos^2x\ dx\).
Solution
We have a composition of functions as \(\cos^2x = \big(\cos x\big)^2\).
However, setting \(u = \cos x\) means \(du = -\sin x\ dx\), which we do not have in the integral. Another technique is needed.
The process we'll employ is to use a Power Reducing formula for \(\cos^2x\) (perhaps consult the back of this text for this formula), which states
\[\cos ^2x = \frac{1+\cos(2x)}{2}.\]
The right hand side of this equation is not difficult to integrate. We have:
\[\begin{align} \int \cos^2x\ dx &= \int \frac{1+\cos(2x)}2\ dx \\ &= \int \left( \frac12 + \frac12\cos(2x)\right)\ dx. \end{align} \]
Now use Key Idea 10:
\[\begin{align} &= \frac12x + \frac12\frac{\sin(2x)}{2} + C\\&= \frac12x + \frac{\sin(2x)}4 + C.\end{align}\]
We'll make significant use of this power--reducing technique in future sections.
Simplifying the Integrand
It is common to be reluctant to manipulate the integrand of an integral; at first, our grasp of integration is tenuous and one may think that working with the integrand will improperly change the results. Integration by substitution works using a different logic: as long as equality is maintained, the integrand can be manipulated so that its form is easier to deal with. The next two examples demonstrate common ways in which using algebra first makes the integration easier to perform.
Example \(\PageIndex{10}\): Integration by substitution: simplifying first
Evaluate \(\displaystyle \int \frac{x^3+4x^2+8x+5}{x^2+2x+1}\ dx\).
Solution
One may try to start by setting \(u\) equal to either the numerator or denominator; in each instance, the result is not workable.
When dealing with rational functions (i.e., quotients made up of polynomial functions), it is an almost universal rule that everything works better when the degree of the numerator is less than the degree of the denominator. Hence we use polynomial division.
We skip the specifics of the steps, but note that when \(x^2+2x+1\) is divided into \(x^3+4x^2+8x+5\), it goes in \(x+2\) times with a remainder of \(3x+3\). Thus
\[\frac{x^3+4x^2+8x+5}{x^2+2x+1} = x+2 + \frac{3x+3}{x^2+2x+1}.\]
Integrating \(x+2\) is simple. The fraction can be integrated by setting \(u = x^2+2x+1\), giving \(du = (2x+2)\ dx\). This is very similar to the numerator. Note that \(du/2 = (x+1)\ dx\) and then consider the following:
\[\begin{align}\int \frac{x^3+4x^2+8x+5}{x^2+2x+1}\ dx & = \int \left(x+2 + \frac{3x+3}{x^2+2x+1}\right)\ dx \\ &= \int (x+2)\ dx + \int \frac{3(x+1)}{x^2+2x+1}\ dx \\ & = \frac12x^2+2x+C_1 + \int \frac{3}{u}\frac{du}{2} \\ &= \frac12x^2+2x+C_1 + \frac32\ln|u| + C_2 \\&= \frac12x^2+2x+\frac32\ln|x^2+2x+1| + C.\end{align}\]
In some ways, we "lucked out" in that after dividing, substitution was able to be done. In later sections we'll develop techniques for handling rational functions where substitution is not directly feasible.
Example \(\PageIndex{11}\): Integration by alternate methods
Evaluate \(\displaystyle \int \frac{x^2+2x+3}{\sqrt{x}}\ dx\) with, and without, substitution.
Solution
We already know how to integrate this particular example. Rewrite \(\sqrt{x}\) as \(x^\frac12\) and simplify the fraction:
\[ \frac{x^2+2x+3}{x^{1/2}} = x^\frac32 + 2x^\frac12 + 3x^{-\frac12}.\]
We can now integrate using the Power Rule:
\[\begin{align} \int \frac{x^2+2x+3}{x^{1/2}}\ dx &= \int\left(x^\frac32 + 2x^\frac12 + 3x^{-\frac12}\right)\ dx\\ &= \frac25x^\frac52 + \frac43x^\frac32 + 6x^\frac12 + C\end{align}\]
This is a perfectly fine approach. We demonstrate how this can also be solved using substitution as its implementation is rather clever.
Let \(u = \sqrt{x} = x^\frac12\); therefore
\[du = \frac12x^{-\frac12}dx = \frac{1}{2\sqrt{x}}\ dx \quad \Rightarrow \quad 2du = \frac{1}{\sqrt{x}}\ dx.\]
This gives us \(\displaystyle \int \frac{x^2+2x+3}{\sqrt{x}}\ dx = \int (x^2+2x+3)\cdot2\ du\). What are we to do with the other \(x\) terms? Since \(u = x^\frac12\), \(u^2 = x\), etc. We can then replace \(x^2\) and \(x\) with appropriate powers of \(u\). We thus have
\[\begin{align*}\int \frac{x^2+2x+3}{\sqrt{x}}\ dx &= \int (x^2+2x+3)\cdot2\ du\\ &= \int 2(u^4 + 2u^2 + 3)\ du \\ &= \frac25u^5 + \frac43u^3 + 6u + C \\&= \frac25x^\frac52 + \frac43x^\frac32 + 6x^\frac12+C,\end{align*}\]
which is obviously the same answer we obtained before. In this situation, substitution is arguably more work than our other method. The fantastic thing is that it works. It demonstrates how flexible integration is.
Substitution and Inverse Trigonometric Functions
When studying derivatives of inverse functions, we learned that
\[\frac{d}{dx}\big(\tan^{-1}x\big) = \frac{1}{1+x^2}.\]
Applying the Chain Rule to this is not difficult; for instance,
\[\frac{d}{dx}\big(\tan^{-1}5x\big) = \frac{5}{1+25x^2}.\]
We now explore how Substitution can be used to "undo" certain derivatives that are the result of the Chain Rule applied to Inverse Trigonometric functions. We begin with an example.
Example \(\PageIndex{12}\): Integrating by substitution: inverse trigonometric functions
Evaluate \( \int \frac{1}{25+x^2}\ dx\).
Solution
The integrand looks similar to the derivative of the arctangent function. Note:
\[\begin{align}\frac{1}{25+x^2} &= \frac{1}{25(1+\frac{x^2}{25})}\\ &= \frac{1}{25(1+\left(\frac{x}{5}\right)^2)} \\
&= \frac{1}{25}\frac{1}{1+\left(\frac{x}{5}\right)^2}\ .\end{align}\]
Thus
\[\int\frac{1}{25+x^2}\ dx = \frac{1}{25}\int \frac{1}{1+\left(\frac{x}{5}\right)^2}\ dx.\]
This can be integrated using Substitution. Set \(u = x/5\), hence \(du = dx/5\) or \(dx=5du\). Thus
\[\begin{align}\int\frac{1}{25+x^2}\ dx &= \frac{1}{25}\int \frac{1}{1+\left(\frac{x}{5}\right)^2}\ dx \\ &= \frac15\int \frac{1}{1+u^2}\ du \\ &= \frac15\tan^{-1}u + C \\ &= \frac15\tan^{-1}\left(\frac x5\right)+C\end{align}\]
Example \(\PageIndex{12}\) demonstrates a general technique that can be applied to other integrands that result in inverse trigonometric functions. The results are summarized here.
Theorem \(\PageIndex{2}\): Integrals Involving Inverse Trigonomentric Functions
Let \(a>0\).
- \(\displaystyle \int \frac{1}{a^2+x^2}\ dx = \frac1a\tan^{-1}\left(\frac{x}{a}\right) + C\)
- \(\displaystyle \int \frac{1}{\sqrt{a^2-x^2}}\ dx = \sin^{-1}\left(\frac{x}{a}\right)+C\)
- \(\displaystyle \int \frac{1}{x\sqrt{x^2-a^2}}\ dx = \frac1a\sec^{-1}\left(\frac{|x|}{a}\right)+C\)
Let's practice using Theorem \(\PageIndex{2}\).
Example \(\PageIndex{13}\): Integrating by substitution: inverse trigonometric functions
Evaluate the given indefinite integrals.
\[ \displaystyle \int \frac{1}{9+x^2}\ dx,\quad \int \frac{1}{x\sqrt{x^2-\frac{1}{100}}}\ dx\quad \text{ and }\quad \int \frac{1}{\sqrt{5-x^2}}\ dx.\]
Solution
Each can be answered using a straightforward application of Theorem \(\PageIndex{2}\).
\(\displaystyle \int \frac{1}{9+x^2}\ dx = \frac13\tan^{-1} \frac x3 + C\), as \(a = 3\).
\(\displaystyle \int \frac{1}{x\sqrt{x^2-\frac{1}{100}}}\ dx = 10\sec^{-1}10x + C\), as \(a = \frac1{10}\).
\(\displaystyle \int \frac{1}{\sqrt{5-x^2}} = \sin^{-1}\frac{x}{\sqrt{5}}+C\), as \(a = \sqrt{5}\).
Most applications of Theorem \(\PageIndex{2}\) are not as straightforward. The next examples show some common integrals that can still be approached with this theorem.
Example \(\PageIndex{14}\): Integrating by substitution: completing the square
Evaluate \(\displaystyle \int\frac{1}{x^2-4x+13}\ dx\).
Solution
Initially, this integral seems to have nothing in common with the integrals in Theorem \(\PageIndex{2}\). As it lacks a square root, it almost certainly is not related to arcsine or arcsecant. It is, however, related to the arctangent function.
We see this by completing the square in the denominator. We give a brief reminder of the process here.
Start with a quadratic with a leading coefficient of 1. It will have the form of \(x^2 + bx + c\). Take 1/2 of \(b\), square it, and add/subtract it back into the expression. I.e.,
\[\begin{align} x^2+bx+ c &= \underbrace{x^2 + bx + \frac{b^2}4}_{(x+b/2)^2} - \frac{b^2}4 + c\\&= \left(x+\frac b2\right)^2 + c-\frac{b^2}4\end{align}\]
In our example, we take half of \(-4\) and square it, getting \(4\). We add/subtract it into the denominator as follows:
\[\begin{align}\frac{1}{x^2-4x+13} &= \frac{1}{\underbrace{x^2-4x+4}_{(x-2)^2}-4+13}\\ &=\frac{1}{(x-2)^2 + 9}\end{align}\]
We can now integrate this using the arctangent rule. Technically, we need to substitute first with \(u=x-2\), but we can employ Key Idea 10 instead. Thus we have
\[ \int \frac{1}{x^2-4x+13}\ dx = \int \frac{1}{(x-2)^2+9}\ dx = \frac13\tan^{-1}\frac{x-2}{3}+C.\]
Example \(\PageIndex{15}\): Integrals requiring multiple methods
Evaluate \(\displaystyle \int \frac{4-x}{\sqrt{16-x^2}}\ dx\).
Solution
This integral requires two different methods to evaluate it. We get to those methods by splitting up the integral:
\[ \int \frac{4-x}{\sqrt{16-x^2}}\ dx = \int \frac{4}{\sqrt{16-x^2}}\ dx - \int \frac{x}{\sqrt{16-x^2}}\ dx.\]
The first integral is handled using a straightforward application of Theorem \(\PageIndex{2}\); the second integral is handled by substitution, with \(u = 16-x^2\). We handle each separately.
\(\displaystyle \int \frac{4}{\sqrt{16-x^2}}\ dx = 4\sin^{-1}\frac{x}{4} + C.\)
\(\displaystyle \int\frac{x}{\sqrt{16-x^2}}\ dx\): Set \(u = 16-x^2\), so \(du = -2xdx\) and \(xdx = -du/2\). We have
\[\begin{align} \int\frac{x}{\sqrt{16-x^2}}\ dx &= \int\frac{-du/2}{\sqrt{u}}\\ &= -\frac12\int \frac{1}{\sqrt{u}}\ du \\ &= - \sqrt{u} + C\\ &= -\sqrt{16-x^2} + C.\end{align}\]
Combining these together, we have
\[ \int \frac{4-x}{\sqrt{16-x^2}}\ dx = 4\sin^{-1}\frac x4 + \sqrt{16-x^2}+C.\]
Substitution and Definite Integration
This section has focused on evaluating indefinite integrals as we are learning a new technique for finding antiderivatives. However, much of the time integration is used in the context of a definite integral. Definite integrals that require substitution can be calculated using the following workflow:
- Start with a definite integral \(\displaystyle \int_a^b f(x)\ dx\) that requires substitution.
- Ignore the bounds; use substitution to evaluate \(\displaystyle \int f(x)\ dx\) and find an antiderivative \(F(x)\).
- Evaluate \(F(x)\) at the bounds; that is, evaluate \(F(x)\Big|_a^b = F(b) - F(a)\).
This workflow works fine, but substitution offers an alternative that is powerful and amazing (and a little time saving).
At its heart, (using the notation of Theorem \(\PageIndex{1}\) substitution converts integrals of the form \(\displaystyle \int F'(g(x))g'(x)\ dx\) into an integral of the form \(\displaystyle \int F'(u)\ du\) with the substitution of \(u = g(x)\). The following theorem states how the bounds of a definite integral can be changed as the substitution is performed.
Theorem \(\PageIndex{3}\): Substitution with Definite Integrals
Let \(F\) and \(g\) be differentiable functions, where the range of \(g\) is an interval \(I\) that is contained in the domain of \(F\). Then
\[\int_a^b F'\big(g(x)\big)g'(x)\ dx = \int_{g(a)}^{g(b)} F'(u)\ du.\]
In effect, Theorem \(\PageIndex{3}\) states that once you convert to integrating with respect to \(u\), you do not need to switch back to evaluating with respect to \(x\). A few examples will help one understand.
Example \(\PageIndex{16}\): Definite integrals and substitution: changing the bounds
Evaluate \(\displaystyle \int_0^2 \cos(3x-1)\ dx\) using Theorem \(\PageIndex{3}\).
Solution
Observing the composition of functions, let \(u=3x-1\), hence \(du = 3dx. As \(3dx\)\) does not appear in the integrand, divide the latter equation by 3 to get \(du/3 = dx\).
By setting \(u = 3x-1\), we are implicitly stating that \(g(x) = 3x-1\). Theorem \(\PageIndex{3}\) states that the new lower bound is \(g(0) = -1\); the new upper bound is \(g(2) = 5\). We now evaluate the definite integral:
\[\begin{align}\int_1^2 \cos(3x-1) \ dx &= \int_{-1}^5 \cos u \frac{du}{3} \\ &= \frac{1}{3} \sin u\Big|_{-1}^5 \\ &= \frac{1}{3}\big(\sin 5- \sin (-1)\big)\approx -0.039.\end{align}\]
Notice how once we converted the integral to be in terms of \(u\), we never went back to using \(x\).
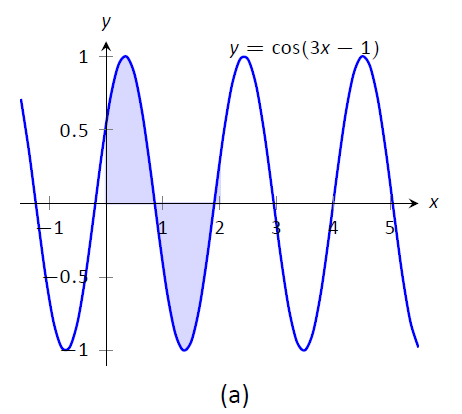
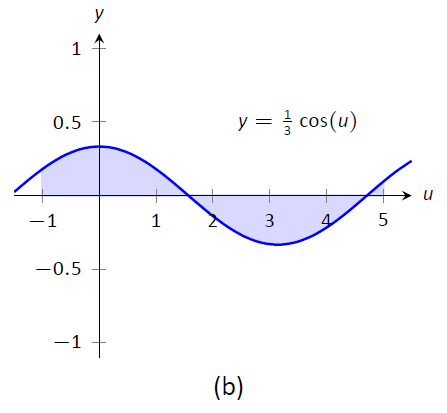
Figure \(\PageIndex{1}\): Graphing the areas defined by the definite integrals of Example \(\PageIndex{16}\)
The graphs in Figure \(\PageIndex{1}\) tell more of the story. In (a) the area defined by the original integrand is shaded, whereas in (b) the area defined by the new integrand is shaded. In this particular situation, the areas look very similar; the new region is "shorter" but "wider," giving the same area.
Example \(\PageIndex{17}\): Definite integrals and substitution: changing the bounds
Evaluate \(\displaystyle \int_0^{\pi/2} \sin x \cos x\ dx\) using Theorem \(\PageIndex{3}\).
Solution
We saw the corresponding indefinite integral in Example \(\PageIndex{4}\). In that example we set \(u = \sin x\) but stated that we could have let \(u = \cos x\). For variety, we do the latter here.
Let \(u = g(x) = \cos x\), giving \(du = -\sin x\ dx\) and hence \(\sin x\ dx = -du\). The new upper bound is \(g(\pi/2) = 0\); the new lower bound is \(g(0) = 1\). Note how the lower bound is actually larger than the upper bound now. We have
\[\begin{align} \int_0^{\pi/2} \sin x\cos x\ dx &= \int_1^0 -u\ du \quad \text{\scriptsize (switch bounds \& change sign)}\\ &= \int_0^1 u\ du\\ &= \frac12u^2\Big|_0^1= 1/2.\\ \end{align}\]
In Figure \(\PageIndex{2}\) we have again graphed the two regions defined by our definite integrals. Unlike the previous example, they bear no resemblance to each other. However, Theorem \(\PageIndex{3}\) guarantees that they have the same area.
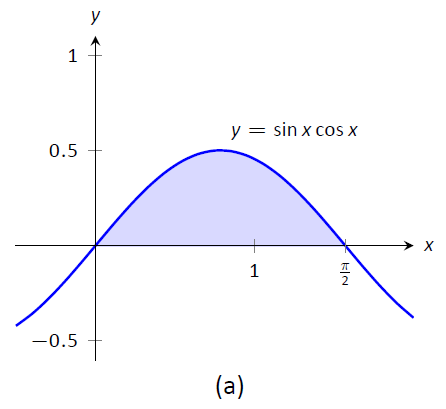
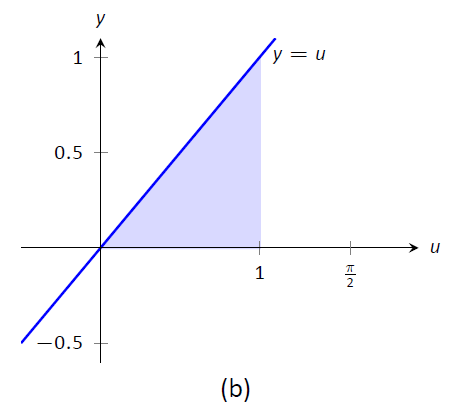
Figure \(\PageIndex{2}\): Graphing the areas defined by the definite integrals of Example \(\PageIndex{17}\).
Integration by substitution is a powerful and useful integration technique. The next section introduces another technique, called Integration by Parts. As substitution "undoes" the Chain Rule, integration by parts "undoes" the Product Rule. Together, these two techniques provide a strong foundation on which most other integration techniques are based.
Contributors and Attributions
Gregory Hartman (Virginia Military Institute). Contributions were made by Troy Siemers and Dimplekumar Chalishajar of VMI and Brian Heinold of Mount Saint Mary's University. This content is copyrighted by a Creative Commons Attribution - Noncommercial (BY-NC) License. http://www.apexcalculus.com/
Integrated by Justin Marshall.


