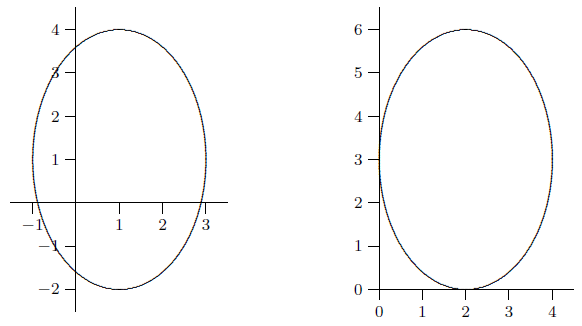1.5: Shifts and Dilations
- Page ID
- 444
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Many functions in applications are built up from simple functions by inserting constants in various places. It is important to understand the effect such constants have on the appearance of the graph.
Horizontal shifts
If we replace \(x\) by \(x-C\) everywhere it occurs in the formula for \(f(x)\), then the graph shifts over \(C\) to the right. (If \(C\) is negative, then this means that the graph shifts over \(|C|\) to the left.) For example, the graph of \(y=(x-2)^2\) is the \(x^2\)-parabola shifted over to have its vertex at the point 2 on the \(x\)-axis. The graph of \(y=(x+1)^2\) is the same parabola shifted over to the left so as to have its vertex at \(-1\) on the \(x\)-axis. Note well: when replacing \(x\) by \(x-C\) we must pay attention to meaning, not merely appearance. Starting with \(y=x^2\) and literally replacing \(x\) by \(x-2\) gives \(y=x-2^2\). This is \(y=x-4\), a line with slope 1, not a shifted parabola.
Vertical shifts
If we replace \(y\) by \(y-D\), then the graph moves up \(D\) units. (If \(D\) is negative, then this means that the graph moves down \(|D|\) units.) If the formula is written in the form \(y=f(x)\) and if \(y\) is replaced by \(y-D\) to get \(y-D=f(x)\), we can equivalently move D to the other side of the equation and write \(y=f(x)+D\). Thus, this principle can be stated: to get the graph of \(y=f(x)+D\), take the graph of \(y=f(x)\) and move it D units up.For example, the function \(y=x^2-4x=(x-2)^2-4\) can be obtained from \(y=(x-2)^2\) (see the last paragraph) by moving the graph 4 units down. The result is the \(x^2\)-parabola shifted 2 units to the right and 4 units down so as to have its vertex at the point \((2,-4)\).
Warning. Do not confuse \(f(x)+D\) and \(f(x+D)\). For example, if \(f(x)\) is the function \(x^2\), then \(f(x)+2\) is the function \(x^2+2\), while \(f(x+2)\) is the function \((x+2)^2=x^2+4x+4\).
We will later want to use two more principles concerning the effects of constants on the appearance of the graph of a function.
Horizontal dilation
If \(x\) is replaced by \(x/A\) in a formula and \(A>1\), then the effect on the graph is to expand it by a factor of \(A\) in the \(x\)-direction (away from the \(y\)-axis). If \(A\) is between 0 and 1 then the effect on the graph is to contract by a factor of \(1/A\) (towards the \(y\)-axis). We use the word "dilate'' to mean expand or contract.
For example, replacing \(x\) by \(x/0.5=x/(1/2)=2x\) has the effect of contracting toward the \(y\)-axis by a factor of 2. If \(A\) is negative, we dilate by a factor of \(|A|\) and then flip about the \(y\)-axis. Thus, replacing \(x\) by \(-x\) has the effect of taking the mirror image of the graph with respect to the \(y\)-axis. For example, the function \(y=\sqrt{-x}\), which has domain \(\{x\in R\mid x\le 0\}\), is obtained by taking the graph of \(\sqrt{x}\) and flipping it around the \(y\)-axis into the second quadrant.
Vertical dilation
If \(y\) is replaced by \(y/B\) in a formula and \(B>0\), then the effect on the graph is to dilate it by a factor of \(B\) in the vertical direction. As before, this is an expansion or contraction depending on whether \(B\) is larger or smaller than one. Note that if we have a function \(y=f(x)\), replacing \(y\) by \(y/B\) is equivalent to multiplying the function on the right by \(B\): \(y=Bf(x)\). The effect on the graph is to expand the picture away from the \(x\)-axis by a factor of \(B\) if \(B>1\), to contract it toward the \(x\)-axis by a factor of \(1/B\) if \(0 < B < 1\), and to dilate by \(|B|\) and then flip about the \(x\)-axis if \(B\) is negative.
Finally, if we want to analyze a function that involves both shifts and dilations, it is usually simplest to work with the dilations first, and then the shifts. For instance, if we want to dilate a function by a factor of \(A\) in the \(x\)-direction and then shift \(C\) to the right, we do this by replacing \(x\) first by \(x/A\) and then by \((x-C)\) in the formula. As an example, suppose that, after dilating our unit circle by \(a\) in the \(x\)-direction and by \(b\) in the \(y\)-direction to get the ellipse in the last paragraph, we then wanted to shift it a distance \(h\) to the right and a distance \(k\) upward, so as to be centered at the point \((h,k)\). The new ellipse would have equation \[ \left({x-h\over a}\right)^2+\left({y-k\over b}\right)^2=1. \nonumber \] Note well that this is different than first doing shifts by \(h\) and \(k\) and then dilations by \(a\) and \(b\):
\[ \left({x\over a}-h\right)^2+\left({y\over b}-k\right)^2=1. \nonumber \]
See figure 1.4.1.