2.E: Instantaneous Rate of Change- The Derivative (Exercises)
- Page ID
- 3463
These are homework exercises to accompany David Guichard's "General Calculus" Textmap. Complementary General calculus exercises can be found for other Textmaps and can be accessed here.
2.1: The Slope of a Function
Ex 2.1.1 Draw the graph of the function \( y=f(x)=\sqrt{169-x^2}\) between \(x=0\) and \(x=13\). Find the slope \(\Delta y/\Delta x\) of the chord between the points of the circle lying over (a) \(x=12\) and \(x=13\), (b) \(x=12\) and \(x=12.1\), (c) \(x=12\) and \(x=12.01\), (d) \(x=12\) and \(x=12.001\). Now use the geometry of tangent lines on a circle to find (e) the exact value of the derivative \(f'(12)\). Your answers to (a)--(d) should be getting closer and closer to your answer to (e). (answer)
Ex 2.1.2 Use geometry to find the derivative \(f'(x)\) of the function \( f(x)=\sqrt{625-x^2}\) in the text for each of the following \(x\): (a) 20, (b) 24, (c) \(-7\), (d) \(-15\). Draw a graph of the upper semicircle, and draw the tangent line at each of these four points. (answer)
Ex 2.1.3 Draw the graph of the function \(y=f(x)=1/x\) between \(x=1/2\) and \(x=4\). Find the slope of the chord between (a) \(x=3\) and \(x=3.1\), (b) \(x=3\) and \(x=3.01\), (c) \(x=3\) and \(x=3.001\). Now use algebra to find a simple formula for the slope of the chord between \((3,f(3))\) and \((3+\Delta x,f(3+\Delta x))\). Determine what happens when \(\Delta x\) approaches 0. In your graph of \(y=1/x\), draw the straight line through the point \((3,1/3)\) whose slope is this limiting value of the difference quotient as \(\Delta x\) approaches 0. (answer)
Ex 2.1.4 Find an algebraic expression for the difference quotient \( \bigl(f(1+\Delta x)-f(1)\bigr)/\Delta x\) when \( f(x)=x^2-(1/x)\). Simplify the expression as much as possible. Then determine what happens as \(\Delta x\) approaches 0. That value is \(f'(1)\). (answer)
Ex 2.1.5 Draw the graph of \( y=f(x)=x^3\) between \(x=0\) and \(x=1.5\). Find the slope of the chord between (a) \(x=1\) and \(x=1.1\), (b) \(x=1\) and \(x=1.001\), (c) \(x=1\) and \(x=1.00001\). Then use algebra to find a simple formula for the slope of the chord between \(1\) and \(1+\Delta x\). (Use the expansion \( (A+B)^3=A^3+3A^2B+3AB^2+B^3\).) Determine what happens as \(\Delta x\) approaches 0, and in your graph of \( y=x^3\) draw the straight line through the point \((1,1)\) whose slope is equal to the value you just found. (answer)
Ex 2.1.6 Find an algebraic expression for the difference quotient \((f(x+\Delta x)-f(x))/\Delta x\) when \(f(x)=mx+b\). Simplify the expression as much as possible. Then determine what happens as \(\Delta x\) approaches 0. That value is \(f'(x)\). (answer)
Ex 2.1.7 Sketch the unit circle. Discuss the behavior of the slope of the tangent line at various angles around the circle. Which trigonometric function gives the slope of the tangent line at an angle \(\theta$? Why? Hint: think in terms of ratios of sides of triangles.
Ex 2.1.8 Sketch the parabola \( y=x^2\). For what values of \(x\) on the parabola is the slope of the tangent line positive? Negative? What do you notice about the graph at the point(s) where the sign of the slope changes from positive to negative and vice versa?
2.2: An Example
Ex 2.2.1 An object is traveling in a straight line so that its position (that is, distance from some fixed point) is given by this table:
| time (seconds) | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| distance (meters) | 0 | 10 | 25 | 60 |
Find the average speed of the object during the following time intervals: \([0,1]\), \([0,2]\), \([0,3]\), \([1,2]\), \([1,3]\), \([2,3]\). If you had to guess the speed at \(t=2\) just on the basis of these, what would you guess? (answer)
Ex 2.2.2 Let \( y=f(t)=t^2\), where \(t\) is the time in seconds and \(y\) is the distance in meters that an object falls on a certain airless planet. Draw a graph of this function between \(t=0\) and \(t=3\). Make a table of the average speed of the falling object between (a) 2 sec and 3 sec, (b) 2 sec and 2.1 sec, (c) 2 sec and 2.01 sec, (d) 2 sec and 2.001 sec. Then use algebra to find a simple formula for the average speed between time \(2\) and time \(2+ \Delta t\). (If you substitute \(\Delta t=1,\>0.1,\>0.01,\>0.001\) in this formula you should again get the answers to parts (a)--(d).) Next, in your formula for average speed (which should be in simplified form) determine what happens as \(\Delta t\) approaches zero. This is the instantaneous speed. Finally, in your graph of \( y=t^2\) draw the straight line through the point \((2,4)\) whose slope is the instantaneous velocity you just computed; it should of course be the tangent line. (answer)
Ex 2.2.3If an object is dropped from an 80-meter high window, its height \(y\) above the ground at time \(t\) seconds is given by the formula \( y=f(t)=80-4.9t^2\). (Here we are neglecting air resistance; the graph of this function was shown in figure 1.0.1.) Find the average velocity of the falling object between (a) 1 sec and 1.1 sec, (b) 1 sec and 1.01 sec, (c) 1 sec and 1.001 sec. Now use algebra to find a simple formula for the average velocity of the falling object between 1 sec and \(1+\Delta t\) sec. Determine what happens to this average velocity as \(\Delta t\) approaches 0. That is the instantaneous velocity at time \(t=1\) second (it will be negative, because the object is falling). (answer)
2.3: Limits
Compute the limits. If a limit does not exist, explain why.
Ex 2.3.1 \( \lim_{x\to 3}{x^2+x-12\over x-3}\) (answer)
Ex 2.3.2 \( \lim_{x\to 1}{x^2+x-12\over x-3}\) (answer)
Ex 2.3.3 \( \lim_{x\to -4}{x^2+x-12\over x-3}\) (answer)
Ex 2.3.4 \( \lim_{x\to 2} {x^2+x-12\over x-2}\) (answer)
Ex 2.3.5 \( \lim_{x\to 1} {\sqrt{x+8}-3\over x-1}\) (answer)
Ex 2.3.6 \( \lim_{x\to 0^+} \sqrt{{1\over x}+2} - \sqrt{1\over x}\). (answer)
Ex 2.3.7 \( \lim _{x\to 2} 3\) (answer)
Ex 2.3.8 \( \lim _{x\to 4 } 3x^3 - 5x \) (answer)
Ex 2.3.9 \( \lim _{x\to 0 } {4x - 5x^2\over x-1}\) (answer)
Ex 2.3.10 \( \lim _{x\to 1 } {x^2 -1 \over x-1 }\) (answer)
Ex 2.3.11 \( \lim _{x\to 0^ + } {\sqrt{2-x^2 }\over x}\) (answer)
Ex 2.3.12 \( \lim _{x\to 0^ + } {\sqrt{2-x^2}\over x+1}\) (answer)
Ex 2.3.13 \( \lim _{x\to a } {x^3 -a^3\over x-a}\) (answer)
Ex 2.3.14 \( \lim _{x\to 2 } (x^2 +4)^3\) (answer)
Ex 2.3.15 \( \lim _{x\to 1 } \cases{ x-5 & \(x\neq 1\),\cr 7 & \(x=1\).\cr}\) (answer)
Ex 2.3.16 \( \lim _{x\to 0 } x\sin \left( {1\over x}\right)\) (Hint: Use the fact that \(|\sin a | < 1 \) for any real number \(a\). You should probably use the definition of a limit here.) (answer)
Ex 2.3.17 Give an \(\epsilon$--$\delta\) proof, similar to example 2.3.3, of the fact that \( \lim_{x\to 4} (2x-5) = 3\).
Ex 2.3.18 Evaluate the expressions by reference to this graph:
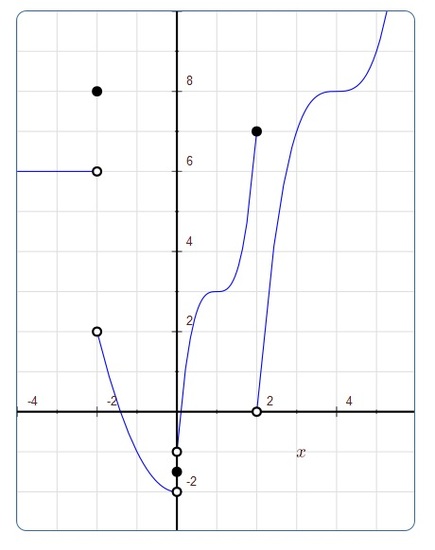
| (a) \( \lim_{x\to 4} f(x)\) | (b) \( \lim_{x\to -3} f(x)\) | (c) \( \lim_{x\to 0} f(x)\) |
| (d) \( \lim_{x\to 0^-} f(x)\) | (e) \( \lim_{x\to 0^+} f(x)\) | (f) \( f(-2)\) |
| (g) \( \lim_{x\to 2^-} f(x)\) | (h) \( \lim_{x\to -2^-} f(x)\) | (i) \( \lim_{x\to 0} f(x+1)\) |
| (j) \( f(0)\) | (k) \( \lim_{x\to 1^-} f(x-4)\) | (l) \( \lim_{x\to 0^+} f(x-2)\) |
(answer)
Ex 2.3.19 Use a calculator to estimate \( \lim_{x\to 0} {\sin x\over x}\).
Ex 2.3.20 Use a calculator to estimate \( \lim_{x\to 0} {\tan(3x)\over\tan(5x)}\).
2.4: The Derivative Function
Ex 2.4.1 Find the derivative of \( y=f(x)=\sqrt{169-x^2}\). (answer)
Ex 2.4.2 Find the derivative of \( y=f(t)=80-4.9t^2\). (answer)
Ex 2.4.3 Find the derivative of \( y=f(x)=x^2-(1/x)\). (answer)
Ex 2.4.4 Find the derivative of \( y=f(x)= ax^2+bx+c\) (where \(a\), \(b\), and \(c\) are constants). (answer)
Ex 2.4.5 Find the derivative of \( y=f(x)=x^3\). (answer)
Ex 2.4.6 Shown is the graph of a function \(f(x)\). Sketch the graph of \(f'(x)\) by estimating the derivative at a number of points in the interval: estimate the derivative at regular intervals from one end of the interval to the other, and also at "special'' points, as when the derivative is zero. Make sure you indicate any places where the derivative does not exist.
Ex 2.4.9 Find the derivative of \(y=g(t)=(2t-1)/(t+2)\) (answer)
Ex 2.4.10 Find an equation for the tangent line to the graph of \( f(x)=5-x-3x^2\) at the point \(x=2\) (answer)
Ex 2.4.11 Find a value for \(a\) so that the graph of \( f(x)=x^2+ax-3\) has a horizontal tangent line at \(x=4\). (answer)
2.5: Adjectives for Functions
Ex 2.5.1 Along the lines of Figure 2.5.1, for each part below sketch the graph of a function that is:
- bounded, but not continuous.
- differentiable and unbounded.
- continuous at \(x=0\), not continuous at \(x=1\), and bounded.
- differentiable everywhere except at \(x=-1\), continuous, and unbounded.
Ex 2.5.2 Is \(f(x)=\sin(x)\) a bounded function? If so, find the smallest \(M\).
Ex 2.5.3 Is \( s(t) = 1/(1+t^2)\) a bounded function? If so, find the smallest \(M\).
Ex 2.5.4 Is \(v(u) = 2\ln|u|\) a bounded function? If so, find the smallest \(M\).
Ex 2.5.5 Consider the function \( h(x) = \cases{ 2x - 3, & if \(x < 1$\cr 0, & if \(x\geq 1\).} \) Show that it is continuous at the point \(x=0\). Is \(h\) a continuous function?
Ex 2.5.6 Approximate a root of \( f=x^3-4x^2+2x+2\) to one decimal place.
Ex 2.5.7 Approximate a root of \( f=x^4+x^3-5x+1\) to one decimal place.


