4.11: Hyperbolic Functions
- Page ID
- 474
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)The hyperbolic functions appear with some frequency in applications, and are quite similar in many respects to the trigonometric functions. This is a bit surprising given our initial definitions.
The hyperbolic cosine is the function
\[\cosh x ={e^x +e^{-x }\over2}, \nonumber \]
and the hyperbolic sine is the function
\[\sinh x ={e^x -e^{-x}\over 2}. \nonumber \]
Notice that \(\cosh\) is even (that is, \(\cosh(-x)=\cosh(x)\)) while \(\sinh\) is odd (\(\sinh(-x)=-\sinh(x)\)), and \( \cosh x + \sinh x = e^x\). Also, for all \(x\), \(\cosh x >0\), while \(\sinh x=0\) if and only if \( e^x -e^{-x }=0\), which is true precisely when \(x=0\).
The range of \(\cosh x\) is \([1,\infty)\).
Let \(y= \cosh x\). We solve for \(x\):
\[\eqalign{y&={e^x +e^{-x }\over 2}\cr 2y &= e^x + e^{-x }\cr 2ye^x &= e^{2x} + 1\cr 0 &= e^{2x}-2ye^x +1\cr e^{x} &= {2y \pm \sqrt{4y^2 -4}\over 2}\cr e^{x} &= y\pm \sqrt{y^2 -1}\cr} \nonumber \]
From the last equation, we see \( y^2 \geq 1\), and since \(y\geq 0\), it follows that \(y\geq 1\).
Now suppose \(y\geq 1\), so \( y\pm \sqrt{y^2 -1}>0\). Then \( x = \ln(y\pm \sqrt{y^2 -1})\) is a real number, and \(y =\cosh x\), so \(y\) is in the range of \(\cosh(x)\).
\(\square\)
The other hyperbolic functions are
\[\eqalign{\tanh x &= {\sinh x\over\cosh x}\cr \coth x &= {\cosh x\over\sinh x}\cr \text{sech} x &= {1\over\cosh x}\cr \text{csch} x &= {1\over\sinh x}\cr} \nonumber \]
The domain of \(\coth\) and \(\text{csch}\) is \(x\neq 0\) while the domain of the other hyperbolic functions is all real numbers. Graphs are shown in Figure \(\PageIndex{1}\)
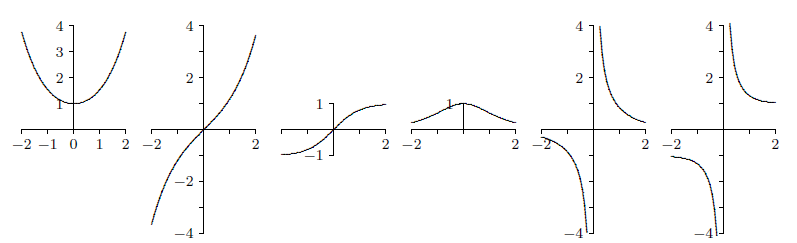
Certainly the hyperbolic functions do not closely resemble the trigonometric functions graphically. But they do have analogous properties, beginning with the following identity.
For all \(x\) in \(\mathbb{R}\), \( \cosh ^2 x -\sinh ^2 x = 1\).
The proof is a straightforward computation:
\[\cosh ^2 x -\sinh ^2 x = {(e^x +e^{-x} )^2\over 4} -{(e^x -e^{-x} )^2\over 4}= {e^{2x} + 2 + e^{-2x } - e^{2x } + 2 - e^{-2x}\over 4}= {4\over 4} = 1. \nonumber \]
\(\square\)
This immediately gives two additional identities:
\[1-\tanh^2 x =\text{sech}^2 x\qquad\hbox{and}\qquad \coth^2 x - 1 =\text{csch}^2 x. \nonumber \]
The identity of the theorem also helps to provide a geometric motivation. Recall that the graph of \( x^2 -y^2 =1\) is a hyperbola with asymptotes \(x=\pm y\) whose \(x\)-intercepts are \(\pm 1\). If \((x,y)\) is a point on the right half of the hyperbola, and if we let \(x=\cosh t\), then \( y=\pm\sqrt{x^2-1}=\pm\sqrt{\cosh^2x-1}=\pm\sinh t\). So for some suitable \(t\), \(\cosh t\) and \(\sinh t\) are the coordinates of a typical point on the hyperbola. In fact, it turns out that \(t\) is twice the area shown in the first graph of Figure \(\PageIndex{2}\). Even this is analogous to trigonometry; \(\cos t\) and \(\sin t\) are the coordinates of a typical point on the unit circle, and \(t\) is twice the area shown in the second graph of Figure \(\PageIndex{2}\).
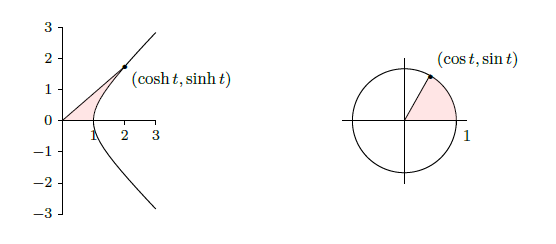
Given the definitions of the hyperbolic functions, finding their derivatives is straightforward. Here again we see similarities to the trigonometric functions.
\( {d\over dx}\cosh x=\sinh x\) and \thmrdef{thm:hyperbolic derivatives} \( {d\over dx}\sinh x = \cosh x\).
\[ {d\over dx}\cosh x= {d\over dx}{e^x +e^{-x}\over 2} = {e^x- e^{-x}\over 2} =\sinh x, \nonumber \]
and
\[ {d\over dx}\sinh x = {d\over dx}{e^x -e^{-x}\over 2} = {e^x +e^{-x }\over 2} =\cosh x. \nonumber \]
Since \(\cosh x > 0\), \(\sinh x\) is increasing and hence injective, so \(\sinh x\) has an inverse, \(\text{arcsinh} x\). Also, \(\sinh x > 0\) when \(x>0\), so \(\cosh x\) is injective on \([0,\infty)\) and has a (partial) inverse, \(\text{arccosh} x\). The other hyperbolic functions have inverses as well, though \(\text{arcsech} x\) is only a partial inverse. We may compute the derivatives of these functions as we have other inverse functions.
\( {d\over dx}\text{arcsinh} x = {1\over\sqrt{1+x^2}}\).
Let \(y=\text{arcsinh} x\), so \(\sinh y=x\). Then
\[ {d\over dx}\sinh y = \cosh(y)\cdot y' = 1, \nonumber \]
and so
\[ y' ={1\over\cosh y} ={1\over\sqrt{1 +\sinh^2 y}} = {1\over\sqrt{1+x^2}}. \nonumber \]
The other derivatives are left to the exercises.
Contributors
Integrated by Justin Marshall.


