15.7: Change of Variables
- Page ID
- 4829
One of the most useful techniques for evaluating integrals is substitution, both "u-substitution'' and trigonometric substitution, in which we change the variable to something more convenient. As we have seen, sometimes changing from rectangular coordinates to another coordinate system is helpful, and this too changes the variables. This is certainly a more complicated change, since instead of changing one variable for another we change an entire suite of variables, but as it turns out it is really very similar to the kinds of change of variables we already know as substitution.
Let's examine the single variable case again, from a slightly different perspective than we have previously used. Suppose we start with the problem
\[\int_0^1 x^2\sqrt{1-x^2}\,dx; \label{eq1}\]
this computes the area in the left graph of figure~\xrefn{fig:one change of variable}. We use the substitution \(x=\sin u\) to transform the function from \(x^2\sqrt{1-x^2}\) to \(\sin^2u\sqrt{1-\sin^2u}\), and we also convert \(dx\) to \(\cos u\,du\). Finally, we convert the limits 0 and 1 to 0 and \(\pi/2\). This transforms the integral in Equation \ref{eq1}:
\[\int_0^1 x^2\sqrt{1-x^2}\,dx = \int_0^{\pi/2}\sin^2u\sqrt{1-\sin^2u} \cos u\,du.\]
We want to notice that there are three different conversions:
- the main function,
- the differential \(dx\), and
- the interval of integration.
The function is converted to \(\sin^2u\sqrt{1-\sin^2u}\), shown in the right-hand graph of Figure \(\PageIndex{1}\). It is evident that the two curves pictured there have the same \(y\)-values in the same order, but the horizontal scale has been changed. Even though the heights are the same, the two integrals
\[\int_0^1 x^2\sqrt{1-x^2}\,dx\qquad\hbox{and}\qquad \int_0^{\pi/2}\sin^2u\sqrt{1-\sin^2u}\,du \]
are not the same; clearly the right hand area is larger. One way to understand the problem is to note that if both areas are approximated using, say, ten subintervals, that the approximating rectangles on the right are wider than their counterparts on the left, as indicated.
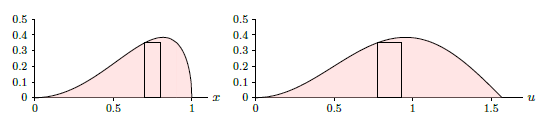
Figure \(\PageIndex{1}\): Single change of variable.
In the picture, the width of the rectangle on the left is \(\Delta x=0.1\), between \(0.7\) and \(0.8\). The rectangle on the right is situated between the corresponding values \(\arcsin(0.7)\) and \(\arcsin(0.8)\) so that \(\Delta u=\arcsin(0.8)-\arcsin(0.7)\). To make the widths match, and the areas therefore the same, we can multiply \(\Delta u\) by a correction factor; in this case the correction factor is approximately \(\cos u=\cos(\arcsin(0.7))\), which we compute when we convert \(dx\) to \(\cos u\,du\). Now let's move to functions of two variables. Suppose we want to convert an integral $$\int_{x_0}^{x_1}\int_{y_0}^{y_1} f(x,y)\,dy\,dx$$ to use new variables \(u\) and \(v\). In the single variable case, there's typically just one reason to want to change the variable: to make the function "nicer'' so that we can find an antiderivative. In the two variable case, there is a second potential reason: the two-dimensional region over which we need to integrate is somehow unpleasant, and we want the region in terms of \(u\) and \(v\) to be nicer---to be a rectangle, for example. Ideally, of course, the new function and the new region will be no worse than the originals, and at least one of them will be better; this doesn't always pan out.
As before, there are three parts to the conversion: the function itself must be rewritten in terms of \(u\) and \(v\), \(dy\,dx\) must be converted to \(du\,dv\), and the old region must be converted to the new region. We will develop the necessary techniques by considering a particular example, and we will use an example we already know how to do by other means.
Consider
\[\int_{-1}^1\int_0^{\sqrt{1-x^2}} \sqrt{x^2+y^2}\,dy\,dx.\]
The limits correspond to integrating over the top half of a circular disk, and we recognize that the function will simplify in polar coordinates, so we would normally convert to polar coordinates:
\[\int_{0}^\pi\int_0^1 \sqrt{r^2}\;r\,dr\,d\theta={\pi\over3}.\]
But let's instead approach this as a substitution problem, starting with \(x=r\cos\theta\), \(y=r\sin\theta\). This pair of equations describes a function from "\(r\)-\(\theta\) space'' to ``\(x\)-\(y\) space'', and because it involves familiar concepts, it is not too hard to understand what it does. In Figure \(\PageIndex{2}\) we have indicated geometrically a bit about how this function behaves. The four dots labeled {\em a}--{\em d} in the \(r\)-\(\theta\) plane correspond to the three dots in the \(x\)-\(y\) plane; dots {\em a} and {\em b} both go to the origin because \(r=0\). The horizontal arrow in the \(r\)-\(\theta\) plane has \(r=1\) everywhere and \(\theta\) ranges from 0 to \(\pi\), so the corresponding points \(x=r\cos\theta\), \(y=r\sin\theta\) start at \((1,0)\) and follow the unit circle counter-clockwise. Finally, the vertical arrow has \(\theta=\pi/4\) and \(r\) ranges from 0 to 1, so it maps to the straight arrow in the \(x\)-\(y\) plane. Extrapolating from these few examples, it's not hard to see that every vertical line in the \(r\)-\(\theta\) plane is transformed to a line through the origin in the \(x\)-\(y\) plane, and every horizontal line in the \(r\)-\(\theta\) plane is transformed to a circle with center at the origin in the \(x\)-\(y\) plane. Since we are interested in integrating over the half-disk in the \(x\)-\(y\) plane, we will integrate over the rectangle \([0,\pi]\times[0,1]\) in the \(r\)-\(\theta\) plane, because we now see that the points in this rectangle are sent precisely to the upper half disk by \(x=r\cos\theta\) and \(y=r\sin\theta\).
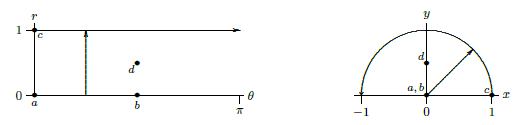
Figure \(\PageIndex{2}\): Double change of variable.
At this point we are two-thirds done with the task: we know the \(r\)-\(\theta\) limits of integration, and we can easily convert the function to the new variables:
\[\eqalignno{\sqrt{x^2+y^2} &= \sqrt{r^2\cos^2\theta+r^2\sin^2\theta}= r\sqrt{\cos^2\theta+\sin^2\theta} = r.&}\]
The final, and most difficult, task is to figure out what replaces \(dx\,dy\). (Of course, we actually know the answer, because we are in effect converting to polar coordinates. What we really want is a series of steps that gets to that right answer but that will also work for other substitutions that are not so familiar.)
Let's take a step back and remember how integration arises from approximation. When we approximate the integral in the \(x\)-\(y\) plane, we are computing the volumes of tall thin boxes, in this case boxes that are \(\Delta x\times \Delta y\times \sqrt{x^2+y^2}\). We are aiming to come up with an integral in the \(r\)- \(\theta\) plane that looks like this:
\[\eqalignno{&\int_0^\pi\int_0^1 r (?) \,dr\,d\theta.&}\]
What we're missing is exactly the right quantity to replace the "?'' so that we get the correct answer. Of course, this integral is also the result of an approximation, in which we add up volumes of boxes that are \(\Delta r\times\Delta \theta\times\hbox{height}\); the problem is that the height that will give us the correct answer is not simply \(r\). Or put another way, we can think of the correct height as \(r\), but the area of the base \(\Delta r\Delta\theta\) as being wrong. The height \(r\) comes from equation~\xrefn{eq:transformed function}, which is to say, it is precisely the same as the corresponding height in the \(x\)-\(y\) version of the integral. The problem is that the area of the base \(\Delta x\times \Delta y\) is not the same as the area of the base \(\Delta r\times\Delta\theta\). We can think of the "?'' in the integral as a correction factor that is needed so that \(?\,dr\,d\theta\) = \(dx\,dy\).
So let's think about what that little base \(\Delta r\times\Delta\theta\) corresponds to. We know that each bit of horizontal line in the \(r\)-\(\theta\) plane corresponds to a bit of circular arc in the \(x\)-\(y\) plane, and each bit of vertical line in the \(r\)-\(\theta\) plane corresponds to a bit of "radial line'' in the \(x\)-\(y\) plane. In Figure \(\PageIndex{3}\) we show a typical rectangle in the \(r\)-\(\theta\) plane and its corresponding area in the \(x\)-\(y\) plane.
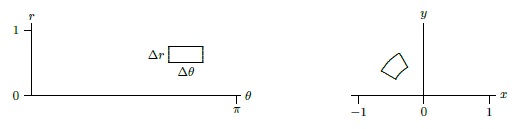
Figure \(\PageIndex{3}\): Corresponding areas.
In this case, the region in the \(x\)-\(y\) plane is approximately a rectangle with dimensions \(\Delta r\times r\Delta\theta\), but in general the corner angles will not be right angles, so the region will typically be (almost) a parallelogram. We need to compute the area of this parallelogram. We know a neat way to do this: compute the length of a certain cross product. If we can determine an appropriate two vectors we'll be nearly done.
Fortunately, we've really done this before. The sides of the region in the \(x\)-\(y\) plane are formed by temporarily fixing either \(r\) or \(\theta\) and letting the other variable range over a small interval. In Figure \(\PageIndex{3}\), for example, the upper right edge of the region is formed by fixing \(\theta=2\pi/3\) and letting \(r\) run from \(0.5\) to \(0.75\). In other words, we have a vector function \({\bf v}(r)=\langle r\cos\theta_0, r\sin\theta_0, 0\rangle\), and we are interested in a restricted set of values for \(r\). A vector tangent to this path is given by the derivative \({\bf v}'(r)=\langle \cos\theta_0, \sin\theta_0, 0\rangle\), and a small tangent vector, with length approximately equal to the side of the region, is \(\langle \cos\theta_0, \sin\theta_0, 0\rangle\,dr\). Likewise, if we fix \(r=r_0=0.5\), we get the vector function \({\bf w}(\theta)=\langle r_0\cos\theta, r_0\sin\theta, 0\rangle\) with derivative \({\bf w}'(\theta)=\langle -r_0\sin\theta, r_0\cos\theta, 0\rangle\) and a small tangent vector \(\langle -r_0\sin\theta_0, r_0\cos\theta_0, 0\rangle\,d\theta\) when \(\theta=\theta_0\) (at the corner we're focusing on). These vectors are shown in Figure \(\PageIndex{4}\), with the actual region outlined by a dotted boundary. Of course, since both \(\Delta r\) and \(\Delta\theta\) are quite large, the parallelogram is not a particularly good approximation to the true area.
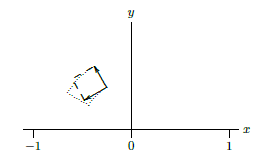
Figure \(\PageIndex{4}\): The approximating parallelogram.
The area of this parallelogram is the length of the cross product:
\[\eqalign{
\langle -r_0\sin\theta_0, r_0\cos\theta_0,
0\rangle\,d\theta\times\langle
\cos\theta_0, \sin\theta_0, 0\rangle\,dr &=
\left|\matrix{{\bf i}&{\bf j}&{\bf k}\cr
-r_0\sin\theta_0&r_0\cos\theta_0&0\cr
\cos\theta_0&\sin\theta_0&0\cr}\right|\,d\theta\,dr\cr
&=\langle 0,0,-r_0\sin^2\theta_0-r_0\cos^2\theta_0\rangle\,d\theta\,dr\cr
&=\langle 0,0,-r_0\rangle\,d\theta\,dr.\cr
}\]
The length of this vector is \(r_0\,dr\,d\theta\). So in general, for any values of \(r\) and \(\theta\), the area in the \(x\)-\(y\) plane corresponding to a small rectangle anchored at \((\theta,r)\) in the \(r\)-\(\theta\) plane is approximately \(r\,dr\,d\theta\). In other words, "\(r\)'' replaces the "?'' in our integral.
In general, a substitution will start with equations \(x=f(u,v)\) and \(y=g(u,v)\). Again, it will be straightforward to convert the function being integrated. Converting the limits will require, as above, an understanding of just how the functions \(f\) and \(g\) transform the \(u\)-\(v\) plane into the \(x\)-\(y\) plane. Finally, the small vectors we need to approximate an area will be \(\langle f_u,g_u,0\rangle\,du\) and \(\langle f_v,g_v,0\rangle\,dv\). The cross product of these is
\[\langle 0,0,f_ug_v-g_uf_v\rangle\,du\,dv\]
with length
\[|f_ug_v-g_uf_v|\,du\,dv.\]
The quantity
\[|f_ug_v-g_uf_v|\]
is usually denoted
\[\left|{\partial(x,y)\over\partial(u,v)}\right|=|f_ug_v-g_uf_v|\]
and called the Jacobian. Note that this is the absolute value of the two-by-two determinant
\[\left|\matrix{f_u&g_u\cr f_v&g_v\cr}\right|,\]
which may be easier to remember.
Confusingly, the matrix, the determinant of the matrix, and the absolute value of the determinant are all called the Jacobian by various authors.
Because there are two things to worry about, namely, the form of the function and the region of integration, transformations in two (or more) variables are quite tricky to discover.
Example \(\PageIndex{1}\):
Integrate \(x^2-xy+y^2\) over the region \(x^2-xy+y^2\le 2\).
Solution
The equation \(x^2-xy+y^2= 2\) describes an ellipse as in Figure \(\PageIndex{5}\); the region of integration is the interior of the ellipse. We will use the transformation \(x=\sqrt2 u-\sqrt{2/3}v\), \(y=\sqrt2 u+\sqrt{2/3}v\). Substituting into the function itself we get
\[x^2-xy+y^2=2u^2+2v^2. \]
The boundary of the ellipse is \(x^2-xy+y^2=2\), so the boundary of the corresponding region in the \(u\)-\(v\) plane is \(2u^2+2v^2=2\) or \(u^2+v^2=1\), the unit circle, so this substitution makes the region of integration simpler.
Next, we compute the Jacobian, using \(f=\sqrt2 u-\sqrt{2/3}v\) and \(g=\sqrt2 u+\sqrt{2/3}v\):
\[f_ug_v-g_uf_v=\sqrt2\sqrt{2/3}+\sqrt2\sqrt{2/3}={4\over\sqrt3}.\]
Hence the new integral is
\[\iint\limits_{R} (2u^2+2v^2){4\over\sqrt3}\,du\,dv,\]
where \(R\) is the interior of the unit circle. This is still not an easy integral, but it is easily transformed to polar coordinates, and then easily integrated.
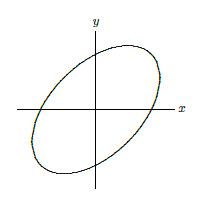
Figure \(\PageIndex{5}\): \( x^2-xy+y^2=2 \)
There is a similar change of variables formula for triple integrals, though it is a bit more difficult to derive. Suppose we use three substitution functions, \(x=f(u,v,w)\), \(y=g(u,v,w)\), and \(z=h(u,v,w)\). The Jacobian determinant is now
\[ {\partial(x,y,z)\over\partial(u,v,w)} =\left|\matrix{f_u&g_u&h_u\cr f_v&g_v&h_v\cr f_w&g_w&h_w\cr}\right|. \]
Then the integral is transformed in a similar fashion:
\[ \iiint\limits_{R} F(x,y,z) \, dV = \iiint \limits_{S} F(f(u,v,w),g(u,v,w),h(u,v,w)) \left|{\partial(x,y,z) \over\partial(u,v,w)}\right| \,du\,dv\,dw, \]
where of course the region \(S\) in \(uvw\) space corresponds to the region \(R\) in \(xyz\) space.
Contributors
Integrated by Justin Marshall.


