1.1E: Exercises for Section 1.1
( \newcommand{\kernel}{\mathrm{null}\,}\)
For exercises 1 - 6, (a) determine the domain and the range of each relation, and (b) state whether the relation is a function.
1)
| x | y | x | y |
|---|---|---|---|
| -3 | 9 | 1 | 1 |
| -2 | 4 | 2 | 4 |
| -1 | 1 | 3 | 9 |
| 0 | 0 |
- Answer
-
a. Domain = {−3,−2,−1,0,1,2,3}, Range = {0,1,4,9}
b. Yes, a function
2)
| x | y | x | y |
|---|---|---|---|
| -3 | -2 | 1 | 1 |
| -2 | -8 | 2 | 8 |
| -1 | -1 | 3 | -2 |
| 0 | 0 |
3)
| x | y | x | y |
|---|---|---|---|
| 1 | -3 | 1 | 1 |
| 2 | -2 | 2 | 2 |
| 3 | -1 | 3 | 3 |
| 0 | 0 |
- Answer
-
a. Domain = {0,1,2,3}, Range = {−3,−2,−1,0,1,2,3}
b. No, not a function
4)
| x | y | x | y |
|---|---|---|---|
| 1 | 1 | 5 | 1 |
| 2 | 1 | 6 | 1 |
| 3 | 1 | 7 | 1 |
| 4 | 1 |
5)
| x | y | x | y |
|---|---|---|---|
| 3 | 3 | 15 | 1 |
| 5 | 2 | 21 | 2 |
| 8 | 1 | 33 | 3 |
| 10 | 0 |
- Answer
-
a. Domain = {3,5,8,10,15,21,33}, Range = {0,1,2,3}
b. Yes, a function
6)
| x | y | x | y |
|---|---|---|---|
| -7 | 11 | 1 | -2 |
| -2 | 5 | 3 | 4 |
| -2 | 1 | 6 | 11 |
| 0 | -1 |
For exercises 7 - 13, find the values for each function, if they exist, then simplify.
a. f(0) b. f(1) c. f(3) d. f(−x) e. f(a) f. f(a+h)
7) f(x)=5x−2
- Answer
- a. −2 b. 3 c. 13 d. −5x−2 e. 5a−2 f. 5a+5h−2
8) f(x)=4x2−3x+1
9) f(x)=2x
- Answer
- a. Undefined b. 2 c. 23 d. −2x e. 2a f. 2a+h
10) f(x)=|x−7|+8
11) f(x)=√6x+5
- Answer
- a. √5 b. √11 c. √23 d. √−6x+5 e. √6a+5 f. √6a+6h+5
12) f(x)=x−23x+7
13) f(x)=9
- Answer
- a. 9 b. 9 c. 9 d. 9 e. 9 f. 9
For exercises 14 - 21, find the domain, range, and all zeros/intercepts, if any, of the functions.
14) f(x)=xx2−16
15) g(x)=√8x−1
- Answer
- x≥18;y≥0;x=18; no y-intercept
16) h(x)=3x2+4
17) f(x)=−1+√x+2
- Answer
- x≥−2;y≥−1;x=−1;y=−1+√2
18) f(x)=1x−√9
19) g(x)=3x−4
- Answer
- x≠4;y≠0; no x-intercept; y=−34
20) f(x)=4|x+5|
21) g(x)=√7x−5
- Answer
- x>5;y>0; no intercepts
For exercises 22 - 27, set up a table to sketch the graph of each function using the following values: x=−3,−2,−1,0,1,2,3.
22) f(x)=x2+1
| x | y | x | y |
|---|---|---|---|
| -3 | 10 | 1 | 2 |
| -2 | 5 | 2 | 5 |
| -1 | 2 | 3 | 10 |
| 0 | 1 |
23) f(x)=3x−6
| x | y | x | y |
|---|---|---|---|
| -3 | -15 | 1 | -3 |
| -2 | -12 | 2 | 0 |
| -1 | -9 | 3 | 3 |
| 0 | -6 |
- Answer
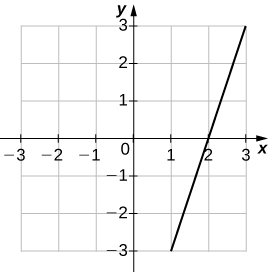
24) f(x)=12x+1
| x | y | x | y |
|---|---|---|---|
| -3 | −12 | 1 | 32 |
| -2 | 0 | 2 | 2 |
| -1 | 12 | 3 | 52 |
| 0 | 1 |
25) f(x)=2|x|
| x | y | x | y |
|---|---|---|---|
| -3 | 6 | 1 | 2 |
| -2 | 4 | 2 | 4 |
| -1 | 2 | 3 | 6 |
| 0 | 0 |
- Answer
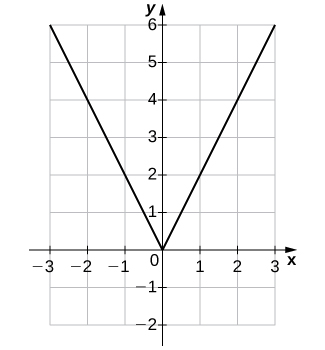
26) f(x)=−x2
| x | y | x | y |
|---|---|---|---|
| -3 | -9 | 1 | -1 |
| -2 | -4 | 2 | -4 |
| -1 | -1 | 3 | -9 |
| 0 | 0 |
27) f(x)=x3
| x | y | x | y |
|---|---|---|---|
| -3 | -27 | 1 | 1 |
| -2 | -8 | 2 | 8 |
| -1 | -1 | 3 | 27 |
| 0 | 0 |
- Answer
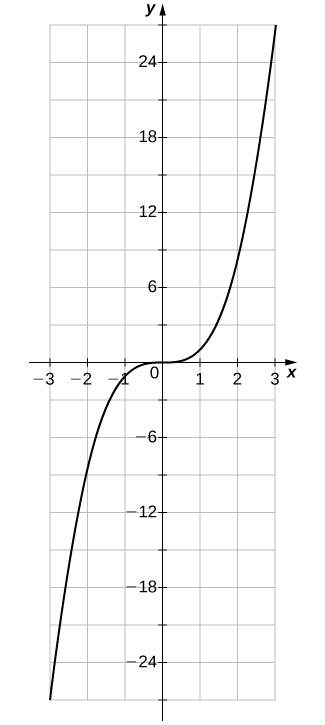
For exercises 28 - 35, use the vertical line test to determine whether each of the given graphs represents a function. Assume that a graph continues at both ends if it extends beyond the given grid. If the graph represents a function, then determine the following for each graph:
a. Domain and range
b. x -intercept, if any (estimate where necessary)
c. y-Intercept, if any (estimate where necessary)
d. The intervals for which the function is increasing
e. The intervals for which the function is decreasing
f. The intervals for which the function is constant
g. Symmetry about any axis and/or the origin
h. Whether the function is even, odd, or neither
28)
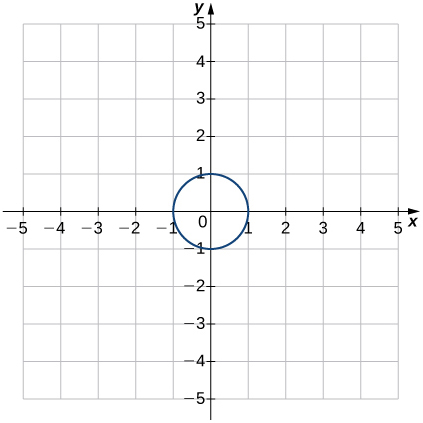
29)
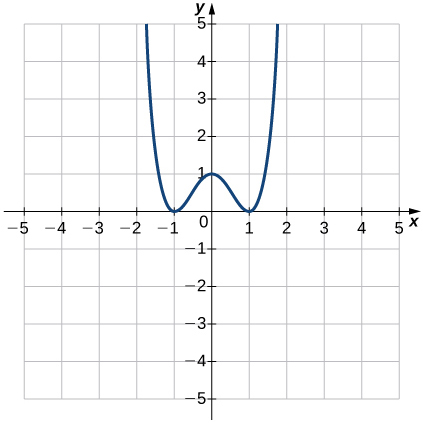
- Answer
- Function;
a. Domain: all real numbers, range: y≥0
b. x=±1
c. y=1
d. −1<x<0 and 1<x<∞
e. −∞<x<−1 and 0<x<1
f. Not constant
g. y-axis
h. Even
30)
31)
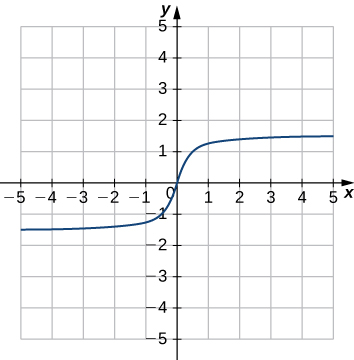
- Answer
- Function;
a. Domain: all real numbers, range: −1.5≤y≤1.5
b. x=0
c. y=0
d. all real numbers
e. None
f. Not constant
g. Origin
h. Odd
32)
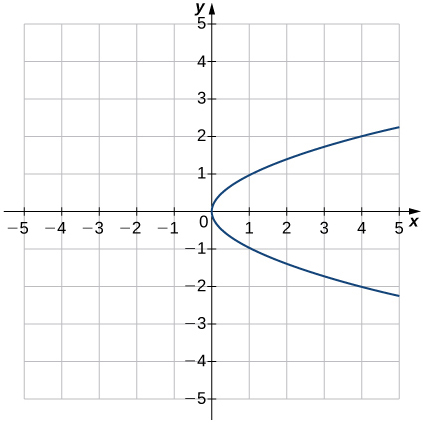
33)
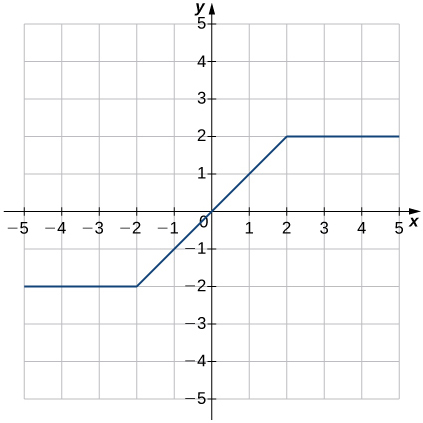
- Answer
- Function;
a. Domain: −∞<x<∞, range: −2≤y≤2
b. x=0
c. y=0
d. −2<x<2
e. Not decreasing
f. −∞<x<−2 and 2<x<∞
g. Origin
h. Odd
34)
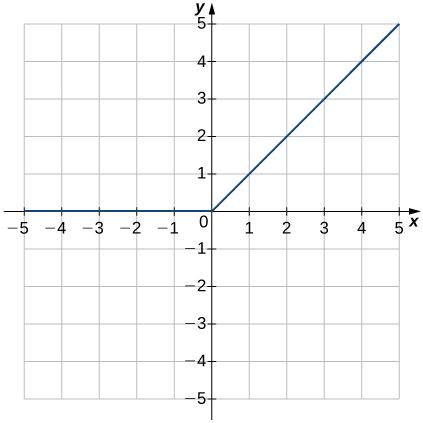
35)
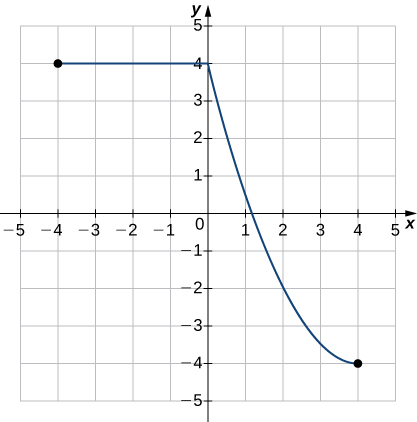
- Answer
- Function;
a. Domain: −4≤x≤4, range: −4≤y≤4
b. x=1.2
c. y=4
d. Not increasing
e. 0<x<4
f. −4<x<0
g. No Symmetry
h. Neither
For exercises 36 - 41, for each pair of functions, find a. f+g b. f−g c. f⋅g d. f/g. Determine the domain of each of these new functions.
36) f(x)=3x+4,g(x)=x−2
37) f(x)=x−8,g(x)=5x2
- Answer
- a. 5x2+x−8; all real numbers
b. −5x2+x−8; all real numbers
c. 5x3−40x2; all real numbers
d. x−85x2;x≠0
38) f(x)=3x2+4x+1,g(x)=x+1
39) f(x)=9−x2,g(x)=x2−2x−3
- Answer
- a. −2x+6; all real numbers
b. −2x2+2x+12; all real numbers
c. −x4+2x3+12x2−18x−27; all real numbers
d. −x+3x+1;x≠−1,3
40) f(x)=√x,g(x)=x−2
41) f(x)=6+1x,g(x)=1x
- Answer
-
a. 6+2x;x≠0
b. 6;x≠0
c. 6x+1x2;x≠0
d. 6x+1;x≠0
For exercises 42 - 48, for each pair of functions, find a. (f∘g)(x) and b. (g∘f)(x) Simplify the results. Find the domain of each of the results.
42) f(x)=3x,g(x)=x+5
43) f(x)=x+4,g(x)=4x−1
- Answer
- a. 4x+3; all real numbers
b. 4x+15; all real numbers
44) f(x)=2x+4,g(x)=x2−2
45) f(x)=x2+7,g(x)=x2−3
- Answer
- a. x4−6x2+16; all real numbers
b. x4+14x2+46; all real numbers
46) f(x)=√x,g(x)=x+9
47) f(x)=32x+1,g(x)=2x
- Answer
-
a. 3x4+x;x≠0,−4
b. 4x+23;x≠−12
48) f(x)=|x+1|,g(x)=x2+x−4
49) The table below lists the NBA championship winners for the years 2001 to 2012.
| Year | Winner |
|---|---|
| 2001 | LA Lakers |
| 2002 | LA Lakers |
| 2003 | Sam Antonio Spurs |
| 2004 | Detroit Pistons |
| 2005 | Sam Antonio Spurs |
| 2006 | Miami Heat |
| 2007 | Sam Antonio Spurs |
| 2008 | Boston Celtics |
| 2009 | LA Lakers |
| 2010 | LA Lakers |
| 2011 | Dallas Mavericks |
| 2012 | Miami Heat |
a. Consider the relation in which the domain values are the years 2001 to 2012 and the range is the corresponding winner. Is this relation a function? Explain why or why not.
b. Consider the relation where the domain values are the winners and the range is the corresponding years. Is this relation a function? Explain why or why not.
- Answer
- a. Yes, because there is only one winner for each year.
b. No, because there are three teams that won more than once during the years 2001 to 2012.
50) [T] The area A of a square depends on the length of the side s.
a. Write a function A(s) for the area of a square.
b. Find and interpret A(6.5).
c. Find the exact and the two-significant-digit approximation to the length of the sides of a square with area 56 square units.
51) [T] The volume of a cube depends on the length of the sides s.
a. Write a function V(s) for the area of a square.
b. Find and interpret V(11.8).
- Answer
- a. V(s)=s3
b. V(11.8)≈1643; a cube of side length 11.8 each has a volume of approximately 1643 cubic units.
52) [T] A rental car company rents cars for a flat fee of $20 and an hourly charge of $10.25. Therefore, the total cost C to rent a car is a function of the hours t the car is rented plus the flat fee.
a. Write the formula for the function that models this situation.
b. Find the total cost to rent a car for 2 days and 7 hours.
c. Determine how long the car was rented if the bill is $432.73.
53) [T] A vehicle has a 20-gal tank and gets 15 mpg. The number of miles N that can be driven depends on the amount of gas x in the tank.
a. Write a formula that models this situation.
b. Determine the number of miles the vehicle can travel on (i) a full tank of gas and (ii) 3/4 of a tank of gas.
c. Determine the domain and range of the function.
d. Determine how many times the driver had to stop for gas if she has driven a total of 578 mi.
- Answer
- a. N(x)=15x
b. i. N(20)=15(20)=300; therefore, the vehicle can travel 300 mi on a full tank of gas.
ii. N(15)=225; therefore, the vehicle can travel 225 mi on 3/4 of a tank of gas.
c. Domain: 0≤x≤20; range: [0,300]
d. The driver had to stop at least once, given that it takes approximately 39 gal of gas to drive a total of 578 mi.
54) [T] The volume V of a sphere depends on the length of its radius as V=(4/3)πr3. Because Earth is not a perfect sphere, we can use the mean radius when measuring from the center to its surface. The mean radius is the average distance from the physical center to the surface, based on a large number of samples. Find the volume of Earth with mean radius 6.371×106 m.
55) [T] A certain bacterium grows in culture in a circular region. The radius of the circle, measured in centimeters, is given by r(t)=6−5t2+1, where t is time measured in hours since a circle of a 1-cm radius of the bacterium was put into the culture.
a. Express the area of the bacteria as a function of time.
b. Find the exact and approximate area of the bacterial culture in 3 hours.
c. Express the circumference of the bacteria as a function of time.
d. Find the exact and approximate circumference of the bacteria in 3 hours.
- Answer
- a. A(t)=A(r(t))=π⋅(6−5t2+1)2
b. Exact: 121π4; approximately 95 cm2
c. C(t)=C(r(t))=2π(6−5t2+1)
d. Exact: 11π; approximately 35 cm
56) [T] An American tourist visits Paris and must convert U.S. dollars to Euros, which can be done using the function E(x)=0.79x, where x is the number of U.S. dollars and E(x) is the equivalent number of Euros. Since conversion rates fluctuate, when the tourist returns to the United States 2 weeks later, the conversion from Euros to U.S. dollars is D(x)=1.245x, where x is the number of Euros and D(x) is the equivalent number of U.S. dollars.
a. Find the composite function that converts directly from U.S. dollars to U.S. dollars via Euros. Did this tourist lose value in the conversion process?
b. Use (a) to determine how many U.S. dollars the tourist would get back at the end of her trip if she converted an extra $200 when she arrived in Paris.
57) [T] The manager at a skateboard shop pays his workers a monthly salary S of $750 plus a commission of $8.50 for each skateboard they sell.
a. Write a function y=S(x) that models a worker’s monthly salary based on the number of skateboards x he or she sells.
b. Find the approximate monthly salary when a worker sells 25, 40, or 55 skateboards.
c. Use the INTERSECT feature on a graphing calculator to determine the number of skateboards that must be sold for a worker to earn a monthly income of $1400. (Hint: Find the intersection of the function and the line y=1400.)
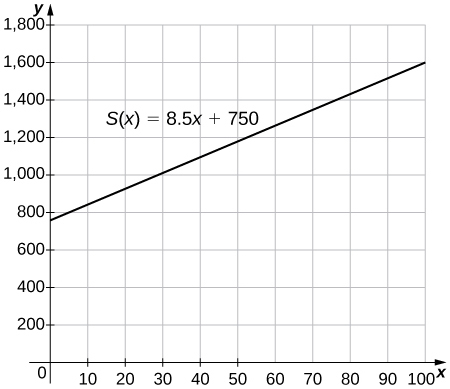
- Answer
- a. S(x)=8.5x+750 b. $962.50, $1090, $1217.50 c. 77 skateboards
58) [T] Use a graphing calculator to graph the half-circle y=√25−(x−4)2. Then, use the INTERCEPT feature to find the value of both the x- and y-intercepts.
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


