1.3: Trigonometric Functions
( \newcommand{\kernel}{\mathrm{null}\,}\)
- Convert angle measures between degrees and radians.
- Recognize the triangular and circular definitions of the basic trigonometric functions.
- Write the basic trigonometric identities.
- Identify the graphs and periods of the trigonometric functions.
- Describe the shift of a sine or cosine graph from the equation of the function.
Trigonometric functions are used to model many phenomena, including sound waves, vibrations of strings, alternating electrical current, and the motion of pendulums. In fact, almost any repetitive, or cyclical, motion can be modeled by some combination of trigonometric functions. In this section, we define the six basic trigonometric functions and look at some of the main identities involving these functions.
Radian Measure
To use trigonometric functions, we first must understand how to measure the angles. Although we can use both radians and degrees, radians are a more natural measurement because they are related directly to the unit circle, a circle with radius 1. The radian measure of an angle is defined as follows. Given an angle θ, let s be the length of the corresponding arc on the unit circle (Figure 1.3.1). We say the angle corresponding to the arc of length 1 has radian measure 1.
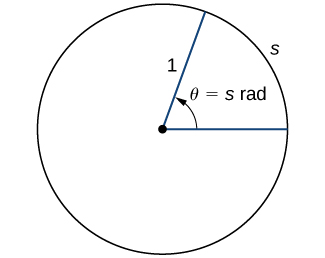
Since an angle of 360° corresponds to the circumference of a circle, or an arc of length 2π, we conclude that an angle with a degree measure of 360° has a radian measure of 2π. Similarly, we see that 180° is equivalent to \pi radians. Table \PageIndex{1} shows the relationship between common degree and radian values.
| Degrees | Radians | Degrees | Radians |
|---|---|---|---|
| 0 | 0 | 120 | 2π/3 |
| 30 | π/6 | 135 | 3π/4 |
| 45 | π/4 | 150 | 5π/6 |
| 60 | π/3 | 180 | π |
| 90 | π/2 |
- Express 225° using radians.
- Express 5π/3 rad using degrees.
Solution
Use the fact that 180° is equivalent to \pi radians as a conversion factor (Table \PageIndex{1}):
1=\dfrac{π \,\mathrm{rad}}{180°}=\dfrac{180°}{π \,\mathrm{rad}}. \nonumber
- 225°=225°⋅\left(\dfrac{π}{180°}\right)=\left(\dfrac{5π}{4}\right) rad
- \dfrac{5π}{3} rad = \dfrac{5π}{3}⋅\dfrac{180°}{π}=300°
- Express 210° using radians.
- Express 11π/6 rad using degrees.
- Hint
-
π radians is equal to 180°
- Answer
-
- 7π/6
- 330°
The Six Basic Trigonometric Functions
Trigonometric functions allow us to use angle measures, in radians or degrees, to find the coordinates of a point on any circle—not only on a unit circle—or to find an angle given a point on a circle. They also define the relationship between the sides and angles of a triangle.
To define the trigonometric functions, first consider the unit circle centered at the origin and a point P=(x,y) on the unit circle. Let θ be an angle with an initial side that lies along the positive x-axis and with a terminal side that is the line segment OP. An angle in this position is said to be in standard position (Figure \PageIndex{2}). We can then define the values of the six trigonometric functions for θ in terms of the coordinates x and y.
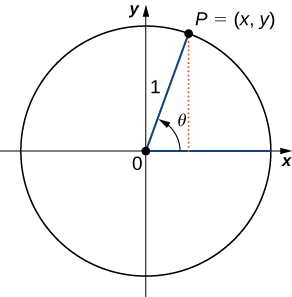
Let P=(x,y) be a point on the unit circle centered at the origin O. Let θ be an angle with an initial side along the positive x-axis and a terminal side given by the line segment OP. The trigonometric functions are then defined as
| \sin θ=y | \csc θ=\dfrac{1}{y} |
| \cos θ=x | \sec θ=\dfrac{1}{x} |
| \tan θ=\dfrac{y}{x} | \cot θ=\dfrac{x}{y} |
If x=0, \sec θ and \tan θ are undefined. If y=0, then \cot θ and \csc θ are undefined.
We can see that for a point P=(x,y) on a circle of radius r with a corresponding angle θ, the coordinates x and y satisfy
\begin{align} \cos θ &=\dfrac{x}{r} \\ x &=r\cos θ \end{align} \nonumber
and
\begin{align} \sin θ &=\dfrac{y}{r} \\ y &=r\sin θ. \end{align} \nonumber
The values of the other trigonometric functions can be expressed in terms of x,y, and r (Figure \PageIndex{3}).
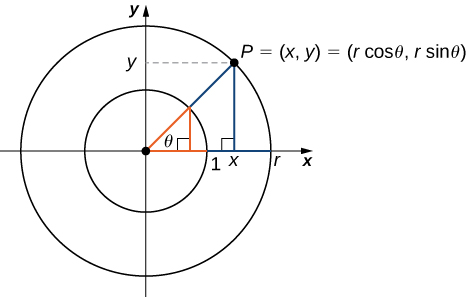
Table \PageIndex{2} shows the values of sine and cosine at the major angles in the first quadrant. From this table, we can determine the values of sine and cosine at the corresponding angles in the other quadrants. The values of the other trigonometric functions are calculated easily from the values of \sin θ and \cos θ.
| θθ | \sin θ | \cos θ |
|---|---|---|
| 0 | 0 | 1 |
| \dfrac{π}{6} | \dfrac{1}{2} | \dfrac{\sqrt{3}}{2} |
| \dfrac{π}{4} | \dfrac{\sqrt{2}}{2} | \dfrac{\sqrt{2}}{2} |
| \dfrac{π}{3} | \dfrac{\sqrt{3}}{2} | \dfrac{1}{2} |
| \dfrac{π}{2} | 1 | 0 |
Evaluate each of the following expressions.
- \sin \left(\dfrac{2π}{3} \right)
- \cos \left(−\dfrac{5π}{6} \right)
- \tan \left(\dfrac{15π}{4}\right)
Solution:
a) On the unit circle, the angle θ=\dfrac{2π}{3} corresponds to the point \left(−\dfrac{1}{2},\dfrac{\sqrt{3}}{2}\right). Therefore,
\sin \left(\dfrac{2π}{3}\right)=y=\left(\dfrac{\sqrt{3}}{2}\right). \nonumber
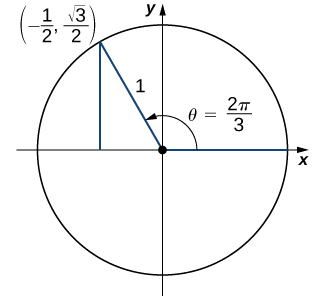
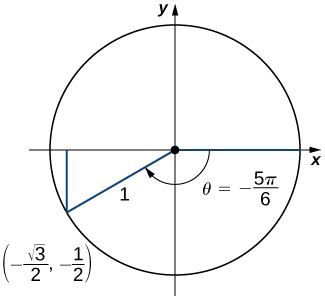
b) An angle θ=−\dfrac{5π}{6} corresponds to a revolution in the negative direction, as shown. Therefore,
\cos \left(−\dfrac{5π}{6}\right)=x=−\dfrac{\sqrt{3}}{2}. \nonumber
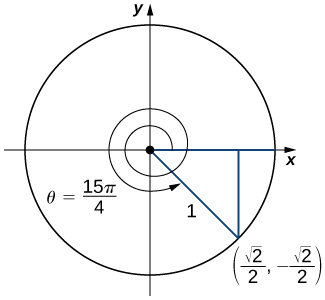
c) An angle θ=\dfrac{15π}{4}=2π+\dfrac{7π}{4}. Therefore, this angle corresponds to more than one revolution, as shown. Knowing the fact that an angle of \dfrac{7π}{4} corresponds to the point (\dfrac{\sqrt{2}}{2},-\dfrac{\sqrt{2}}{2}), we can conclude that
\tan \left(\dfrac{15π}{4}\right)=\dfrac{y}{x}=−1. \nonumber
Evaluate \cos(3π/4) and \sin(−π/6).
- Hint
-
Look at angles on the unit circle.
- Answer
-
\cos(3π/4) = −\sqrt{2}/2\nonumber
\sin(−π/6) =−1/2 \nonumber
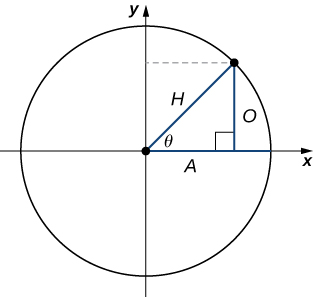
As mentioned earlier, the ratios of the side lengths of a right triangle can be expressed in terms of the trigonometric functions evaluated at either of the acute angles of the triangle. Let θ be one of the acute angles. Let A be the length of the adjacent leg, O be the length of the opposite leg, and H be the length of the hypotenuse. By inscribing the triangle into a circle of radius H, as shown in Figure \PageIndex{4}, we see that A,H, and O satisfy the following relationships with θ:
| \sin θ=\dfrac{O}{H} | \csc θ=\dfrac{H}{O} |
| \cos θ=\dfrac{A}{H} | \sec θ=\dfrac{H}{A} |
| \tan θ=\dfrac{O}{A} | \cot θ=\dfrac{A}{O} |
A wooden ramp is to be built with one end on the ground and the other end at the top of a short staircase. If the top of the staircase is 4 ft from the ground and the angle between the ground and the ramp is to be 10°, how long does the ramp need to be?
Solution
Let x denote the length of the ramp. In the following image, we see that x needs to satisfy the equation \sin(10°)=4/x. Solving this equation for x, we see that x=4/\sin(10°)≈23.035 ft.

A house painter wants to lean a 20-ft ladder against a house. If the angle between the base of the ladder and the ground is to be 60°, how far from the house should she place the base of the ladder?
- Hint
-
Draw a right triangle with hypotenuse 20.
- Answer
-
10 ft
Trigonometric Identities
A trigonometric identity is an equation involving trigonometric functions that is true for all angles θ for which the functions are defined. We can use the identities to help us solve or simplify equations. The main trigonometric identities are listed next.
Reciprocal identities
\tan θ=\dfrac{\sin θ}{\cos θ} \nonumber
\cot θ=\dfrac{\cos θ}{\sin θ} \nonumber
\csc θ=\dfrac{1}{\sin θ} \nonumber
\sec θ=\dfrac{1}{\cos θ} \nonumber
Pythagorean identities
\begin{align} \sin^2θ+\cos^2θ &=1 \label{py1} \\[4pt] 1+\tan^2θ &=\sec^2θ \\[4pt] 1+\cot^2θ &=\csc^2θ \end{align}
Addition and subtraction formulas
\sin(α±β)=\sin α\cos β±\cos α \sin β \nonumber
\cos(α±β)=\cos α\cos β∓\sin α \sin β \nonumber
Double-angle formulas
\sin(2θ)=2\sin θ\cos θ \label{double1}
\begin{align} \cos(2θ) &=2\cos^2θ−1 \\[4pt] &=1−2\sin^2θ \\[4pt] &=\cos^2θ−\sin^2θ \end{align} \nonumber
For each of the following equations, use a trigonometric identity to find all solutions.
- 1+\cos(2θ)=\cos θ
- \sin(2θ)=\tan θ
Solution
a) Using the double-angle formula for \cos(2θ), we see that θ is a solution of
1+\cos(2θ)=\cos θ \nonumber
if and only if
1+2\cos^2θ−1=\cos θ, \nonumber
which is true if and only if
2\cos^2θ−\cos θ=0. \nonumber
To solve this equation, it is important to note that we need to factor the left-hand side and not divide both sides of the equation by \cos θ. The problem with dividing by \cos θ is that it is possible that \cos θ is zero. In fact, if we did divide both sides of the equation by \cos θ, we would miss some of the solutions of the original equation. Factoring the left-hand side of the equation, we see that θ is a solution of this equation if and only if
\cos θ(2\cos θ−1)=0. \nonumber
Since \cos θ=0 when
θ=\dfrac{π}{2},\dfrac{π}{2}±π,\dfrac{π}{2}±2π,…, \nonumber
and \cos θ=1/2 when
θ=\dfrac{π}{3},\dfrac{π}{3}±2π,…\mathrm{or}\ θ=−\dfrac{π}{3},−\dfrac{π}{3}±2π,…, \nonumber
we conclude that the set of solutions to this equation is
θ=\dfrac{π}{2}+nπ,\;θ=\dfrac{π}{3}+2nπ \nonumber
and
θ=−\dfrac{π}{3}+2nπ,\;n=0,±1,±2,….\nonumber
b) Using the double-angle formula for \sin(2θ) and the reciprocal identity for \tan(θ), the equation can be written as
2\sin θ\cos θ=\dfrac{\sin θ}{\cos θ}.\nonumber
To solve this equation, we multiply both sides by \cos θ to eliminate the denominator, and say that if θ satisfies this equation, then θ satisfies the equation
2\sin θ \cos^2θ−\sin θ=0. \nonumber
However, we need to be a little careful here. Even if θ satisfies this new equation, it may not satisfy the original equation because, to satisfy the original equation, we would need to be able to divide both sides of the equation by \cos θ. However, if \cos θ=0, we cannot divide both sides of the equation by \cos θ. Therefore, it is possible that we may arrive at extraneous solutions. So, at the end, it is important to check for extraneous solutions. Returning to the equation, it is important that we factor \sin θ out of both terms on the left-hand side instead of dividing both sides of the equation by \sin θ. Factoring the left-hand side of the equation, we can rewrite this equation as
\sin θ(2\cos^2θ−1)=0. \nonumber
Therefore, the solutions are given by the angles θ such that \sin θ=0 or \cos^2θ=1/2. The solutions of the first equation are θ=0,±π,±2π,…. The solutions of the second equation are θ=π/4,(π/4)±(π/2),(π/4)±π,…. After checking for extraneous solutions, the set of solutions to the equation is
θ=nπ \nonumber
and
θ=\dfrac{π}{4}+\dfrac{nπ}{2} \nonumber
with n=0,±1,±2,….
Find all solutions to the equation \cos(2θ)=\sin θ.
- Hint
-
Use the double-angle formula for cosine (Equation \ref{double1}).
- Answer
-
θ=\dfrac{3π}{2}+2nπ,\dfrac{π}{6}+2nπ,\dfrac{5π}{6}+2nπ
for n=0,±1,±2,….
Prove the trigonometric identity 1+\tan^2θ=\sec^2θ.
Solution:
We start with the Pythagorean identity (Equation \ref{py1})
\sin^2θ+\cos^2θ=1. \nonumber
Dividing both sides of this equation by \cos^2θ, we obtain
\dfrac{\sin^2θ}{\cos^2θ}+1=\dfrac{1}{\cos^2θ}. \nonumber
Since \sin θ/\cos θ=\tan θ and 1/\cos θ=\sec θ, we conclude that
\tan^2θ+1=\sec^2θ. \nonumber
Prove the trigonometric identity 1+\cot^2θ=\csc^2θ.
- Answer
-
Divide both sides of the identity \sin^2θ+\cos^2θ=1 by \sin^2θ.
Graphs and Periods of the Trigonometric Functions
We have seen that as we travel around the unit circle, the values of the trigonometric functions repeat. We can see this pattern in the graphs of the functions. Let P=(x,y) be a point on the unit circle and let θ be the corresponding angle . Since the angle θ and θ+2π correspond to the same point P, the values of the trigonometric functions at θ and at θ+2π are the same. Consequently, the trigonometric functions are periodic functions. The period of a function f is defined to be the smallest positive value p such that f(x+p)=f(x) for all values x in the domain of f. The sine, cosine, secant, and cosecant functions have a period of 2π. Since the tangent and cotangent functions repeat on an interval of length π, their period is π (Figure \PageIndex{5}).
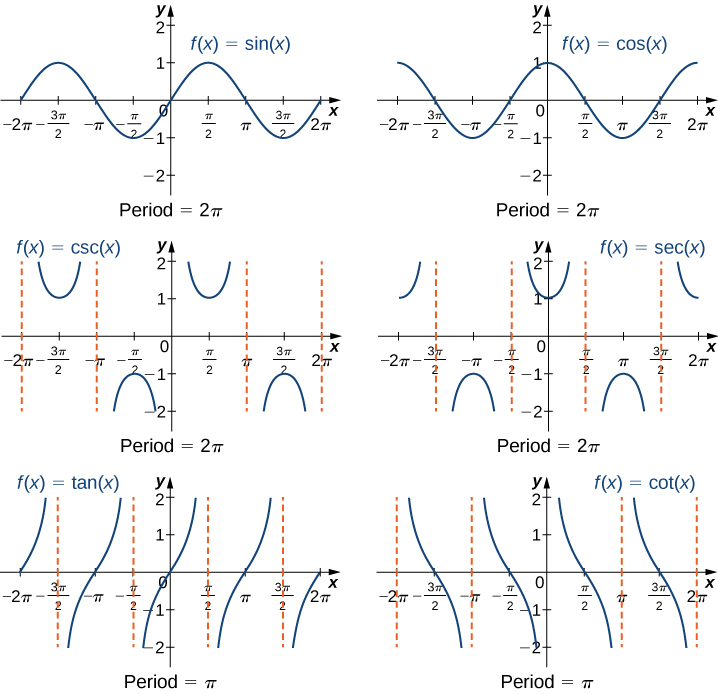
Just as with algebraic functions, we can apply transformations to trigonometric functions. In particular, consider the following function:
f(x)=A\sin(B(x−α))+C. \nonumber
In Figure \PageIndex{6}, the constant α causes a horizontal or phase shift. The factor B changes the period. This transformed sine function will have a period 2π/|B|. The factor A results in a vertical stretch by a factor of |A|. We say |A| is the “amplitude of f.” The constant C causes a vertical shift.
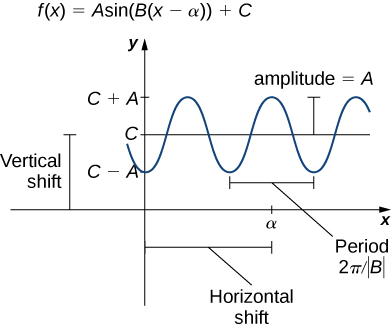
Notice in Figure \PageIndex{6} that the graph of y=\cos x is the graph of y=\sin x shifted to the left π/2 units. Therefore, we can write
\cos x=\sin(x+π/2). \nonumber
Similarly, we can view the graph of y=\sin x as the graph of y=\cos x shifted right π/2 units, and state that \sin x=\cos(x−π/2).
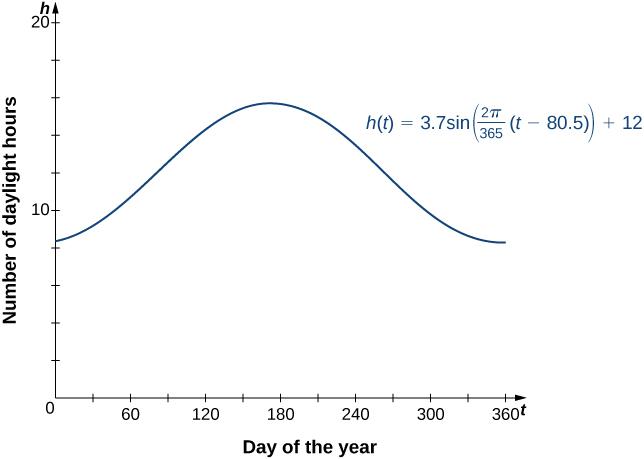
A shifted sine curve arises naturally when graphing the number of hours of daylight in a given location as a function of the day of the year. For example, suppose a city reports that June 21 is the longest day of the year with 15.7 hours and December 21 is the shortest day of the year with 8.3 hours. It can be shown that the function
h(t)=3.7\sin \left(\dfrac{2π}{365}(x−80.5)\right)+12 \nonumber
is a model for the number of hours of daylight h as a function of day of the year t (Figure \PageIndex{7}).
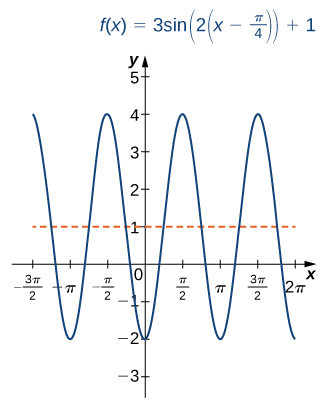
Sketch a graph of f(x)=3\sin(2(x−\frac{π}{4}))+1.
Solution
This graph is a phase shift of y=\sin (x) to the right by π/4 units, followed by a horizontal compression by a factor of 2, a vertical stretch by a factor of 3, and then a vertical shift by 1 unit. The period of f is π.
Describe the relationship between the graph of f(x)=3\sin(4x)−5 and the graph of y=\sin(x).
- Hint
-
The graph of f can be sketched using the graph of y=\sin(x) and a sequence of three transformations.
- Answer
-
To graph f(x)=3\sin(4x)−5, the graph of y=\sin(x) needs to be compressed horizontally by a factor of 4, then stretched vertically by a factor of 3, then shifted down 5 units. The function f will have a period of π/2 and an amplitude of 3.
Key Concepts
- Radian measure is defined such that the angle associated with the arc of length 1 on the unit circle has radian measure 1. An angle with a degree measure of 180° has a radian measure of \pi rad.
- For acute angles θ,the values of the trigonometric functions are defined as ratios of two sides of a right triangle in which one of the acute angles is θ.
- For a general angle θ, let (x,y) be a point on a circle of radius r corresponding to this angle θ. The trigonometric functions can be written as ratios involving x, y, and r.
- The trigonometric functions are periodic. The sine, cosine, secant, and cosecant functions have period 2π. The tangent and cotangent functions have period π.
Key Equations
- Generalized sine function
f(x)=A \sin(B(x−α))+C
Glossary
- periodic function
- a function is periodic if it has a repeating pattern as the values of x move from left to right
- radians
- for a circular arc of length s on a circle of radius 1, the radian measure of the associated angle θ is s
- trigonometric functions
- functions of an angle defined as ratios of the lengths of the sides of a right triangle
- trigonometric identity
- an equation involving trigonometric functions that is true for all angles θ for which the functions in the equation are defined


