1.4E: Exercises for Section 1.4
- Page ID
- 69788
In exercises 1 - 6, use the horizontal line test to determine whether each of the given graphs is one-to-one.
1)
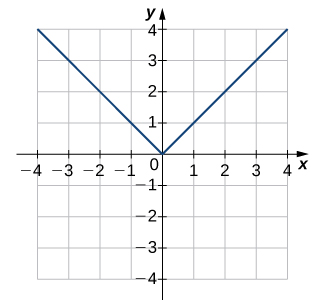
- Answer
- Not one-to-one
2)
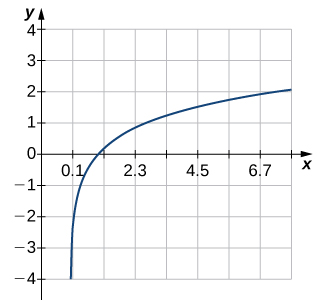
3)
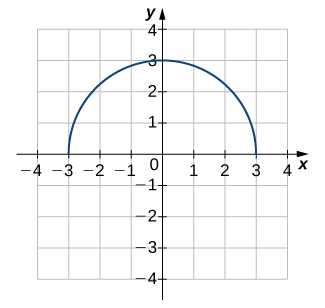
- Answer
- Not one-to-one
4)
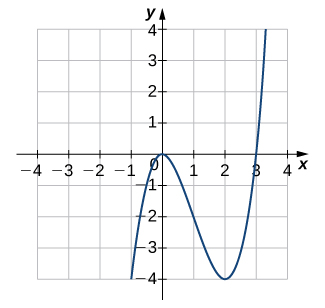
5)
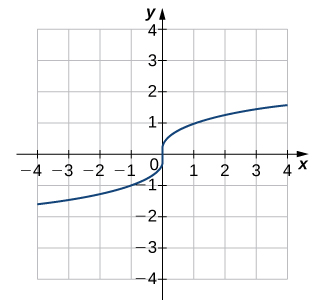
- Answer
- One-to-one
6)
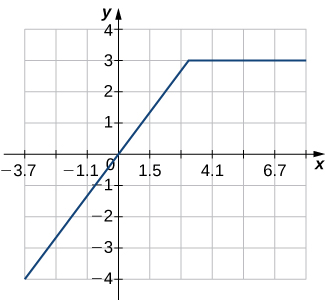
In exercises 7 - 12,
a. find the inverse function, and
b. find the domain and range of the inverse function.
7) \(f(x)=x^2−4, \quad x≥0\)
- Answer
- a. \(f^{−1}(x)=\sqrt{x+4}\)
b. Domain: \(x≥−4,\) Range: \(y≥0\)
8) \(f(x)=\sqrt[3]{x−4}\)
9) \(f(x)=x^3+1\)
- Answer
- a. \(f^{−1}(x)=\sqrt[3]{x−1}\)
b. Domain: all real numbers, Range: all real numbers
10) \(f(x)=(x−1)^2, \quad x≤1\)
11) \(f(x)=\sqrt{x−1}\)
- Answer
- a. \(f^{−1}(x)=x^2+1\),
b. Domain: \(x≥0,\) Range: \(y≥1\)
12) \(f(x)=\dfrac{1}{x+2}\)
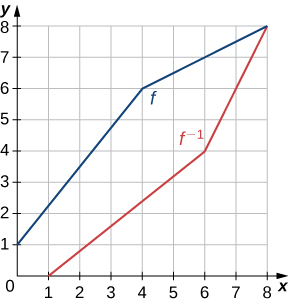
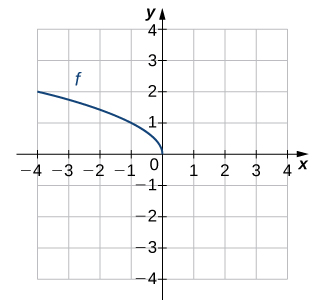
In exercises 13 - 16, use the graph of \(f\) to sketch the graph of its inverse function.
13)
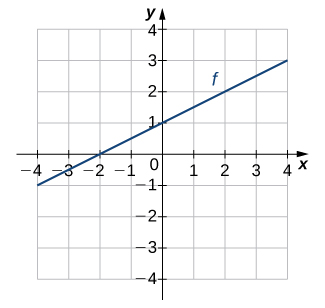
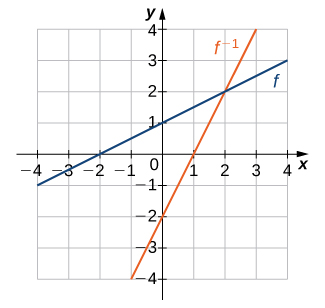
- Answer
14)
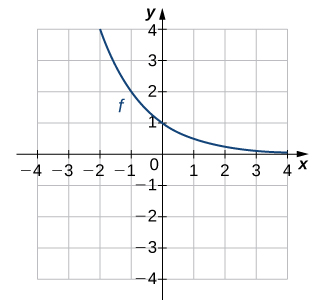
15)
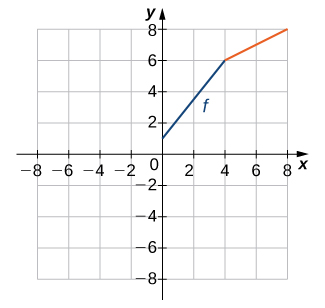
- Answer
16)
In exercises 17 - 24, use composition to determine which pairs of functions are inverses.
17) \(f(x)=8x, \quad g(x)=\dfrac{x}{8}\)
- Answer
- These are inverses.
18) \(f(x)=8x+3, \quad g(x)=\dfrac{x-3}{8}\)
19) \(f(x)=5x−7, \quad g(x)=\dfrac{x+5}{7}\)
- Answer
- These are not inverses.
20) \(f(x)=\frac{2}{3}x+2, \quad g(x)=\frac{3}{2}x+3\)
21) \(f(x)=\dfrac{1}{x−1}, \;x≠1, \quad g(x)=\dfrac{1}{x}+1,\; x≠0\)
- Answer
- These are inverses.
22) \(f(x)=x^3+1,\quad g(x)=(x−1)^{1/3}\)
23) \(f(x)=x^2+2x+1,\; x≥−1, \quad g(x)=−1+\sqrt{x},\; x≥0\)
- Answer
- These are inverses.
24) \(f(x)=\sqrt{4−x^2},\; 0≤x≤2, \quad g(x)=\sqrt{4−x^2},\; 0≤x≤2\)
In exercises 25 - 33, evaluate the functions. Give the exact value.
25) \(\tan^{−1}\left(\frac{\sqrt{3}}{3}\right)\)
- Answer
- \(\frac{π}{6}\)
26) \(\cos^{−1}\left(−\frac{\sqrt{2}}{2}\right)\)
27) \(\cot^{−1}(1)\)
- Answer
- \(\frac{π}{4}\)
28) \(\sin^{−1}(−1)\)
29) \(\cos^{−1}\left(\frac{\sqrt{3}}{2}\right)\)
- Answer
- \(\frac{π}{6}\)
30) \(\cos\big(\tan^{−1}(\sqrt{3})\big)\)
31) \(\sin\left(\cos^{−1}\left(\frac{\sqrt{2}}{2}\right)\right)\)
- Answer
- \(\frac{\sqrt{2}}{2}\)
32) \(\sin^{−1}\left(\sin\left(\frac{π}{3}\right)\right)\)
33) \(\tan^{−1}\left(\tan\left(−\frac{π}{6}\right)\right)\)
- Answer
- \(-\frac{π}{6}\)
34) The function \(C=T(F)=(5/9)(F−32)\) converts degrees Fahrenheit to degrees Celsius.
a) Find the inverse function \(F=T^{−1}(C)\)
b) What is the inverse function used for?
35) [T] The velocity \(V\) (in centimeters per second) of blood in an artery at a distance \(x\) cm from the center of the artery can be modeled by the function \(V=f(x)=500(0.04−x^2)\) for \(0≤x≤0.2.\)
a) Find \(x=f^{−1}(V).\)
b) Interpret what the inverse function is used for.
c) Find the distance from the center of an artery with a velocity of 15 cm/sec, 10 cm/sec, and 5 cm/sec.
- Answer
- a. \(x=f^{−1}(V)=\sqrt{0.04−\dfrac{V}{500}}\)
b. The inverse function determines the distance from the center of the artery at which blood is flowing with velocity \(V.\)
c. 0.1 cm; 0.14 cm; 0.17 cm
36) A function that converts dress sizes in the United States to those in Europe is given by \(D(x)=2x+24.\)
a) Find the European dress sizes that correspond to sizes 6, 8, 10, and 12 in the United States.
b) Find the function that converts European dress sizes to U.S. dress sizes.
c) Use part b. to find the dress sizes in the United States that correspond to 46, 52, 62, and 70.
37) [T] The cost to remove a toxin from a lake is modeled by the function \(C(p)=\dfrac{75p}{85−p},\) where \(C\) is the cost (in thousands of dollars) and \(p\) is the amount of toxin in a small lake (measured in parts per billion [ppb]). This model is valid only when the amount of toxin is less than 85 ppb.
a) Find the cost to remove 25 ppb, 40 ppb, and 50 ppb of the toxin from the lake.
b) Find the inverse function.
c) Use part b. to determine how much of the toxin is removed for $50,000.
- Answer
- a. $31,250, $66,667, $107,143
b. \(p=\dfrac{85C}{C+75}\)
c. 34 ppb
38) [T] A race car is accelerating at a velocity given by \(v(t)=\frac{25}{4}t+54,\)
where \(v\) is the velocity (in feet per second) at time \(t.\)
a) Find the velocity of the car at 10 sec.
b) Find the inverse function.
c) Use part b. to determine how long it takes for the car to reach a speed of 150 ft/sec.
39) [T] An airplane’s Mach number \(M\) is the ratio of its speed to the speed of sound. When a plane is flying at a constant altitude, then its Mach angle is given by \(μ=2\sin^{−1}\left(\frac{1}{M}\right).\)
Find the Mach angle (to the nearest degree) for the following Mach numbers.
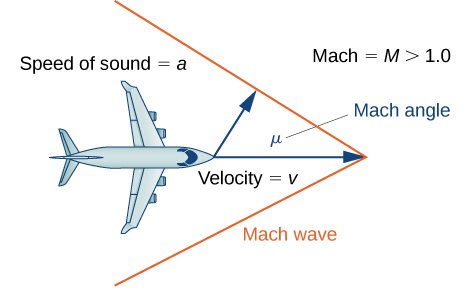
a. \(μ=1.4\)
b. \(μ=2.8\)
c. \(μ=4.3\)
- Answer
- a. \(\sim 92°\) b. \(\sim 42°\) c. \(\sim 27°\)
40) [T] Using \(μ=2\sin^{−1}\left(\frac{1}{M}\right)\), find the Mach number M for the following angles.
a. \(μ=\frac{π}{6}\)
b. \(μ=\frac{2π}{7}\)
c. \(μ=\frac{3π}{8}\)
41) [T] The temperature (in degrees Celsius) of a city in the northern United States can be modeled by the function
\(T(x)=5+18\sin\left[\frac{π}{6}(x−4.6)\right],\)
where \(x\) is time in months and \(x=1.00\) corresponds to January 1. Determine the month and day when the temperature is \(21°C.\)
- Answer
- \(x≈6.69,\, 8.51\); so, the temperature occurs on June 21 and August 15
42) [T] The depth (in feet) of water at a dock changes with the rise and fall of tides. It is modeled by the function \(D(t)=5\sin\left(\frac{π}{6}t−\frac{7π}{6}\right)+8,\) where \(t\) is the number of hours after midnight. Determine the first time after midnight when the depth is \(11.75\) ft.
43) [T] An object moving in simple harmonic motion is modeled by the function \(s(t)=−6\cos\left(\dfrac{πt}{2}\right),\) where \(s\) is measured in inches and \(t\) is measured in seconds. Determine the first time when the distance moved is \(4.5\) in.
- Answer
- \(\sim 1.5\) sec
44) [T] A local art gallery has a portrait 3 ft in height that is hung 2.5 ft above the eye level of an average person. The viewing angle \(θ\) can be modeled by the function \(θ=\tan^{−1}\frac{5.5}{x}−\tan^{−1}\frac{2.5}{x}\), where \(x\) is the distance (in feet) from the portrait. Find the viewing angle when a person is 4 ft from the portrait.
45) [T] Use a calculator to evaluate \(\tan^{−1}(\tan(2.1))\) and \(\cos^{−1}(\cos(2.1))\). Explain the results of each.
- Answer
- \(\tan^{−1}(\tan(2.1))≈−1.0416\); the expression does not equal \(2.1\) since \(2.1>1.57=\frac{π}{2}\)—in other words, it is not in the restricted domain of \(\tan x\). \(\cos^{−1}(\cos(2.1))=2.1\), since \(2.1\) is in the restricted domain of \(\cos x\).
46) [T] Use a calculator to evaluate \(\sin(\sin^{−1}(−2))\) and \(\tan(\tan^{−1}(−2))\). Explain the results of each.
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


