3.9: Derivatives of Exponential and Logarithmic Functions
- Page ID
- 2498
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Find the derivative of exponential functions.
- Find the derivative of logarithmic functions.
- Use logarithmic differentiation to determine the derivative of a function.
So far, we have learned how to differentiate a variety of functions, including trigonometric, inverse, and implicit functions. In this section, we explore derivatives of exponential and logarithmic functions. As we discussed in Introduction to Functions and Graphs, exponential functions play an important role in modeling population growth and the decay of radioactive materials. Logarithmic functions can help rescale large quantities and are particularly helpful for rewriting complicated expressions.
Derivative of the Exponential Function
Just as when we found the derivatives of other functions, we can find the derivatives of exponential and logarithmic functions using formulas. As we develop these formulas, we need to make certain basic assumptions. The proofs that these assumptions hold are beyond the scope of this course.
First of all, we begin with the assumption that the function \(B(x)=b^x,\, b>0,\) is defined for every real number and is continuous. In previous courses, the values of exponential functions for all rational numbers were defined—beginning with the definition of \(b^n\), where \(n\) is a positive integer—as the product of \(b\) multiplied by itself \(n\) times. Later, we defined \(b^0=1,b^{−n}=\dfrac{1}{b^n}\), for a positive integer \(n\), and \(b^{s/t}=(\sqrt[t]{b})^s\) for positive integers \(s\) and \(t\). These definitions leave open the question of the value of \(b^r\) where \(r\) is an arbitrary real number. By assuming the continuity of \(B(x)=b^x,b>0\), we may interpret \(b^r\) as \(\displaystyle \lim_{x→r}b^x\) where the values of \(x\) as we take the limit are rational. For example, we may view \(4^π\) as the number satisfying
\[4^3<4^π<4^4,\quad 4^{3.1}<4^π<4^{3.2},\quad 4^{3.14}<4^π<4^{3.15}, \nonumber \]
\[4^{3.141}<4^{π}<4^{3.142},\quad 4^{3.1415}<4^{π}<4^{3.1416},\quad …. \nonumber \]
As we see in the following table, \(4^π≈77.88.\)
| \(x\) | \(4^x\) | \(x\) | \(4^x\) |
|---|---|---|---|
| \(4^3\) | 64 | \(4^{3.141593}\) | 77.8802710486 |
| \(4^{3.1}\) | 73.5166947198 | \(4^{3.1416}\) | 77.8810268071 |
| \(4^{3.14}\) | 77.7084726013 | \(4^{3.142}\) | 77.9242251944 |
| \(4^{3.141}\) | 77.8162741237 | \(4^{3.15}\) | 78.7932424541 |
| \(4^{3.1415}\) | 77.8702309526 | \(4^{3.2}\) | 84.4485062895 |
| \(4^{3.14159}\) | 77.8799471543 | \(4^{4}\) | 256 |
Approximating a Value of \(4^π\)
We also assume that for \(B(x)=b^x,\, b>0\), the value \(B′(0)\) of the derivative exists. In this section, we show that by making this one additional assumption, it is possible to prove that the function \(B(x)\) is differentiable everywhere.
We make one final assumption: that there is a unique value of \(b>0\) for which \(B′(0)=1\). We define e to be this unique value, as we did in Introduction to Functions and Graphs. Figure \(\PageIndex{1}\) provides graphs of the functions \(y=2^x, \,y=3^x, \,y=2.7^x,\) and \(y=2.8^x\). A visual estimate of the slopes of the tangent lines to these functions at 0 provides evidence that the value of e lies somewhere between 2.7 and 2.8. The function \(E(x)=e^x\) is called the natural exponential function. Its inverse, \(L(x)=\log_e x=\ln x\) is called the natural logarithmic function.
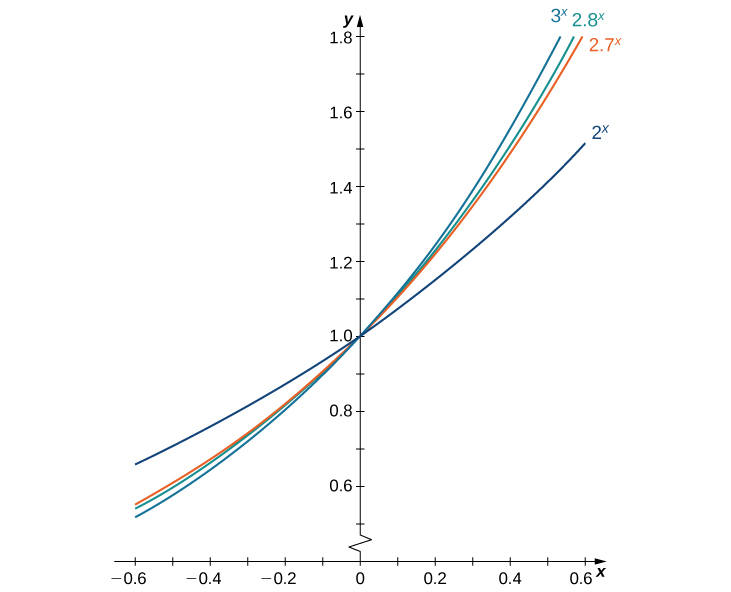
For a better estimate of \(e\), we may construct a table of estimates of \(B′(0)\) for functions of the form \(B(x)=b^x\). Before doing this, recall that
\[B′(0)=\lim_{x→0}\frac{b^x−b^0}{x−0}=\lim_{x→0}\frac{b^x−1}{x}≈\frac{b^x−1}{x} \nonumber \]
for values of \(x\) very close to zero. For our estimates, we choose \(x=0.00001\) and \(x=−0.00001\)
to obtain the estimate
\[\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}. \nonumber \]
See the following table.
| \(b\) | \(\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}.\) | \(b\) | \(\frac{b^{−0.00001}−1}{−0.00001}<B′(0)<\frac{b^{0.00001}−1}{0.00001}.\) |
|---|---|---|---|
| 2 | \(0.693145<B′(0)<0.69315\) | 2.7183 | \(1.000002<B′(0)<1.000012\) |
| 2.7 | \(0.993247<B′(0)<0.993257\) | 2.719 | \(1.000259<B′(0)<1.000269\) |
| 2.71 | \(0.996944<B′(0)<0.996954\) | 2.72 | \(1.000627<B′(0)<1.000637\) |
| 2.718 | \(0.999891<B′(0)<0.999901\) | 2.8 | \(1.029614<B′(0)<1.029625\) |
| 2.7182 | \(0.999965<B′(0)<0.999975\) | 3 | \(1.098606<B′(0)<1.098618\) |
The evidence from the table suggests that \(2.7182<e<2.7183.\)
The graph of \(E(x)=e^x\) together with the line \(y=x+1\) are shown in Figure \(\PageIndex{2}\). This line is tangent to the graph of \(E(x)=e^x\) at \(x=0\).
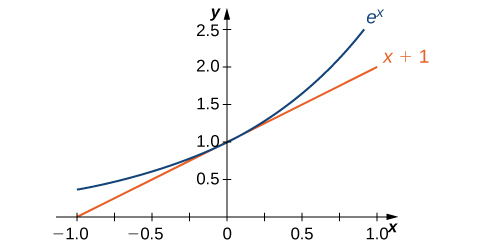
Now that we have laid out our basic assumptions, we begin our investigation by exploring the derivative of \(B(x)=b^x, \,b>0\). Recall that we have assumed that \(B′(0)\) exists. By applying the limit definition to the derivative we conclude that
\[B′(0)=\lim_{h→0}\frac{b^{0+h}−b^0}{h}=\lim_{h→0}\frac{b^h−1}{h} \nonumber \]
Turning to \(B′(x)\), we obtain the following.
\(\begin{aligned} \displaystyle B′(x)&=\lim_{h→0}\frac{b^{x+h}−b^x}{h} & & \text{Apply the limit definition of the derivative.}\\[4pt]
&=\lim_{h→0}\frac{b^xb^h−b^x}{h} & & \text{Note that }b^{x+h}=b^xb^h.\\[4pt]
&=\lim_{h→0}\frac{b^x(b^h−1)}{h} & & \text{Factor out }b^x.\\[4pt]
&=b^x\lim_{h→0}\frac{b^h−1}{h} & & \text{Apply a property of limits.}\\[4pt]
&=b^xB′(0) & & \text{Use } B′(0)=\lim_{h→0}\frac{b^{0+h}−b^0}{h}=\lim_{h→0}\frac{b^h−1}{h}.\end{aligned}\)
We see that on the basis of the assumption that \(B(x)=b^x\) is differentiable at \(0,B(x)\) is not only differentiable everywhere, but its derivative is
\[B′(x)=b^xB′(0).\nonumber \]
For \(E(x)=e^x, \,E′(0)=1.\) Thus, we have \(E′(x)=e^x\). (The value of \(B′(0)\) for an arbitrary function of the form \(B(x)=b^x, \,b>0,\) will be derived later.)
Let \(E(x)=e^x\) be the natural exponential function. Then
\[E′(x)=e^x. \nonumber \]
In general,
\[\frac{d}{dx}\Big(e^{g(x)}\Big)=e^{g(x)}g′(x) \nonumber \]
Find the derivative of \(f(x)=e^{\tan(2x)}\).
Solution:
Using the derivative formula and the chain rule,
\[f′(x)=e^{\tan(2x)}\frac{d}{dx}\Big(\tan(2x)\Big)=e^{\tan(2x)}\sec^2(2x)⋅2 \nonumber \]
Find the derivative of \(y=\dfrac{e^{x^2}}{x}\).
Solution
Use the derivative of the natural exponential function, the quotient rule, and the chain rule.
\(\begin{align*} y′&=\dfrac{(e^{x^2}⋅2)x⋅x−1⋅e^{x^2}}{x^2} & & \text{Apply the quotient rule.}\\[4pt]
&=\dfrac{e^{x^2}(2x^2−1)}{x^2} & & \text{Simplify.} \end{align*}\)
Find the derivative of \(h(x)=xe^{2x}\).
- Hint
-
Don’t forget to use the product rule.
- Answer
-
\(h′(x)=e^{2x}+2xe^{2x}\)
A colony of mosquitoes has an initial population of 1000. After \(t\) days, the population is given by \(A(t)=1000e^{0.3t}\). Show that the ratio of the rate of change of the population, \(A′(t)\), to the population, \(A(t)\) is constant.
Solution
First find \(A′(t)\). By using the chain rule, we have \(A′(t)=300e^{0.3t}.\) Thus, the ratio of the rate of change of the population to the population is given by
\[\frac{A′(t)}{A(t)}=\frac{300e^{0.3t}}{1000e^{0.3t}}=0.3. \nonumber \]
The ratio of the rate of change of the population to the population is the constant 0.3.
If \(A(t)=1000e^{0.3t}\) describes the mosquito population after \(t\) days, as in the preceding example, what is the rate of change of \(A(t)\) after 4 days?
- Hint
-
Find \(A′(4)\).
- Answer
-
\(996\)
Derivative of the Logarithmic Function
Now that we have the derivative of the natural exponential function, we can use implicit differentiation to find the derivative of its inverse, the natural logarithmic function.
If \(x>0\) and \(y=\ln x\), then
\[\frac{dy}{dx}=\frac{1}{x}. \nonumber \]
More generally, let \(g(x)\) be a differentiable function. For all values of \(x\) for which \(g′(x)>0\), the derivative of \(h(x)=\ln(g(x))\) is given by
\[h′(x)=\frac{1}{g(x)}g′(x). \nonumber \]
If \(x>0\) and \(y=\ln x\), then \(e^y=x.\) Differentiating both sides of this equation results in the equation
\[e^y\frac{dy}{dx}=1. \nonumber \]
Solving for \(\dfrac{dy}{dx}\) yields
\[\frac{dy}{dx}=\frac{1}{e^y}. \nonumber \]
Finally, we substitute \(x=e^y\) to obtain
\[\frac{dy}{dx}=\frac{1}{x}. \nonumber \]
We may also derive this result by applying the inverse function theorem, as follows. Since \(y=g(x)=\ln x\)
is the inverse of \(f(x)=e^x\), by applying the inverse function theorem we have
\[\frac{dy}{dx}=\frac{1}{f′(g(x))}=\frac{1}{e^{\ln x}}=\frac{1}{x}. \nonumber \]
Using this result and applying the chain rule to \(h(x)=\ln(g(x))\) yields
\[h′(x)=\frac{1}{g(x)}g′(x). \label{lnder} \]
□
The graph of \(y=\ln x\) and its derivative \(\dfrac{dy}{dx}=\dfrac{1}{x}\) are shown in Figure \(\PageIndex{3}\).
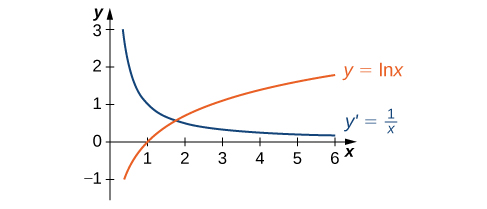
Find the derivative of \(f(x)=\ln(x^3+3x−4)\).
Solution
Use Equation \ref{lnder} directly.
\(\begin{align*} f′(x)&=\dfrac{1}{x^3+3x−4}⋅(3x^2+3) & & \text{Use }g(x)=x^3+3x−4\text{ in }h′(x)=\dfrac{1}{g(x)}g′(x).\\[4pt]
&=\dfrac{3x^2+3}{x^3+3x−4} & & \text{Rewrite.} \end{align*} \)
Find the derivative of \(f(x)=\ln\left(\dfrac{x^2\sin x}{2x+1}\right)\).
Solution
At first glance, taking this derivative appears rather complicated. However, by using the properties of logarithms prior to finding the derivative, we can make the problem much simpler.
\(\begin{align*} f(x)&=\ln\left(\frac{x^2\sin x}{2x+1}\right)=2\ln x+\ln(\sin x)−\ln(2x+1) & & \text{Apply properties of logarithms.}\\[4pt]
f′(x)&=\dfrac{2}{x}+\cot x−\dfrac{2}{2x+1} & & \text{Apply sum rule and }h′(x)=\dfrac{1}{g(x)}g′(x). \end{align*}\)
Differentiate: \(f(x)=\ln(3x+2)^5\).
- Hint
-
Use a property of logarithms to simplify before taking the derivative.
- Answer
-
\(f′(x)=\dfrac{15}{3x+2}\)
Now that we can differentiate the natural logarithmic function, we can use this result to find the derivatives of \(y=\log_b x\) and \(y=b^x\) for \(b>0, \,b≠1\).
Let \(b>0,b≠1,\) and let \(g(x)\) be a differentiable function.
i. If \(y=\log_b x\), then
\[\frac{dy}{dx}=\frac{1}{x\ln b}. \nonumber \]
More generally, if \(h(x)=\log_b(g(x))\), then for all values of \(x\) for which \(g(x)>0\),
\[h′(x)=\frac{g′(x)}{g(x)\ln b}. \label{genlogder} \]
ii. If \(y=b^x,\) then
\[\frac{dy}{dx}=b^x\ln b. \nonumber \]
More generally, if \(h(x)=b^{g(x)},\) then
\[h′(x)=b^{g(x)}g'(x)\ln b \label{genexpder} \]
If \(y=\log_b x,\) then \(b^y=x.\) It follows that \(\ln(b^y)=\ln x\). Thus \(y\ln b=\ln x\). Solving for \(y\), we have \(y=\dfrac{\ln x}{\ln b}\). Differentiating and keeping in mind that \(\ln b\) is a constant, we see that
\[\frac{dy}{dx}=\frac{1}{x\ln b}. \nonumber \]
The derivative in Equation \ref{genlogder} now follows from the chain rule.
If \(y=b^x\). then \(\ln y=x\ln b.\) Using implicit differentiation, again keeping in mind that \(\ln b\) is constant, it follows that \(\dfrac{1}{y}\dfrac{dy}{dx}=\ln b\). Solving for \(\dfrac{dy}{dx}\) and substituting \(y=b^x\), we see that
\[\frac{dy}{dx}=y\ln b=b^x\ln b. \nonumber \]
The more general derivative (Equation \ref{genexpder}) follows from the chain rule.
□
Find the derivative of \(h(x)=\dfrac{3^x}{3^x+2}\).
Solution
Use the quotient rule and Note.
\(\begin{align*} h′(x)&=\dfrac{3^x\ln 3(3^x+2)−3^x\ln 3(3^x)}{(3^x+2)^2} & & \text{Apply the quotient rule.}\\[4pt]
&=\dfrac{2⋅3^x\ln 3}{(3x+2)^2} & & \text{Simplify.} \end{align*}\)
Find the slope of the line tangent to the graph of \(y=\log_2 (3x+1)\) at \(x=1\).
Solution
To find the slope, we must evaluate \(\dfrac{dy}{dx}\) at \(x=1\). Using Equation \ref{genlogder}, we see that
\[\frac{dy}{dx}=\frac{3}{(3x+1)\ln 2}. \nonumber \]
By evaluating the derivative at \(x=1\), we see that the tangent line has slope
\[\frac{dy}{dx}\bigg{|}_{x=1}=\frac{3}{4\ln 2}=\frac{3}{\ln 16}. \nonumber \]
Find the slope for the line tangent to \(y=3^x\) at \(x=2.\)
- Hint
-
Evaluate the derivative at \(x=2.\)
- Answer
-
\(9\ln(3)\)
Logarithmic Differentiation
At this point, we can take derivatives of functions of the form \(y=(g(x))^n\) for certain values of \(n\), as well as functions of the form \(y=b^{g(x)}\), where \(b>0\) and \(b≠1\). Unfortunately, we still do not know the derivatives of functions such as \(y=x^x\) or \(y=x^π\). These functions require a technique called logarithmic differentiation, which allows us to differentiate any function of the form \(h(x)=g(x)^{f(x)}\). It can also be used to convert a very complex differentiation problem into a simpler one, such as finding the derivative of \(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\). We outline this technique in the following problem-solving strategy.
- To differentiate \(y=h(x)\) using logarithmic differentiation, take the natural logarithm of both sides of the equation to obtain \(\ln y=\ln(h(x)).\)
- Use properties of logarithms to expand \(\ln(h(x))\) as much as possible.
- Differentiate both sides of the equation. On the left we will have \(\dfrac{1}{y}\dfrac{dy}{dx}\).
- Multiply both sides of the equation by \(y\) to solve for \(\dfrac{dy}{dx}\).
- Replace \(y\) by \(h(x)\).
Find the derivative of \(y=(2x^4+1)^{\tan x}\).
Solution
Use logarithmic differentiation to find this derivative.
\(\begin{align*} \ln y&=\ln(2x^4+1)^{\tan x} & & \text{Step 1. Take the natural logarithm of both sides.}\\[4pt]
\ln y&=\tan x\ln(2x^4+1) & & \text{Step 2. Expand using properties of logarithms.}\\[4pt]
\dfrac{1}{y}\dfrac{dy}{dx}&=\sec^2 x\ln(2x^4+1)+\dfrac{8x^3}{2x^4+1}⋅\tan x & & \text{Step 3. Differentiate both sides. Use the product rule on the right.}\\[4pt]
\dfrac{dy}{dx}&=y⋅(\sec^2 x\ln(2x^4+1)+\dfrac{8x^3}{2x^4+1}⋅\tan x) & & \text{Step 4. Multiply by }y\text{ on both sides.}\\[4pt]
\dfrac{dy}{dx}&=(2x^4+1)^{\tan x}(\sec^2 x\ln(2x^4+1)+\dfrac{8x^3}{2x^4+1}⋅\tan x) & & \text{Step 5. Substitute }y=(2x^4+1)^{\tan x}. \end{align*}\)
Find the derivative of \(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\).
Solution
This problem really makes use of the properties of logarithms and the differentiation rules given in this chapter.
| \(\ln y=\ln\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\) | Step 1. Take the natural logarithm of both sides. |
| \(\ln y=\ln x+\frac{1}{2}\ln(2x+1)−x\ln e−3\ln \sin x\) | Step 2. Expand using properties of logarithms. |
| \(\dfrac{1}{y}\dfrac{dy}{dx}=\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\dfrac{\cos x}{\sin x}\) | Step 3. Differentiate both sides. |
| \(\dfrac{dy}{dx}=y\left(\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\cot x\right)\) | Step 4. Multiply by \(y\) on both sides. |
| \(\dfrac{dy}{dx}=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}\left(\dfrac{1}{x}+\dfrac{1}{2x+1}−1−3\cot x\right)\) | Step 5. Substitute \(y=\dfrac{x\sqrt{2x+1}}{e^x\sin^3 x}.\) |
Use logarithmic differentiation to find the derivative of \(y=x^x\).
- Hint
-
Follow the problem solving strategy.
- Answer
-
Solution: \(\dfrac{dy}{dx}=x^x(1+\ln x)\)
Find the derivative of \(y=(\tan x)^π\).
- Hint
-
Use the power rule (since the exponent \(\pi\) is a constant) and the chain rule.
- Answer
-
\(y′=π(\tan x)^{π−1}\sec^2 x\)
Key Concepts
- On the basis of the assumption that the exponential function \(y=b^x, \,b>0\) is continuous everywhere and differentiable at \(0\), this function is differentiable everywhere and there is a formula for its derivative.
- We can use a formula to find the derivative of \(y=\ln x\), and the relationship \(\log_b x=\dfrac{\ln x}{\ln b}\) allows us to extend our differentiation formulas to include logarithms with arbitrary bases.
- Logarithmic differentiation allows us to differentiate functions of the form \(y=g(x)^{f(x)}\) or very complex functions by taking the natural logarithm of both sides and exploiting the properties of logarithms before differentiating.
Key Equations
- Derivative of the natural exponential function
\(\dfrac{d}{dx}\Big(e^{g(x)}\Big)=e^{g(x)}g′(x)\)
- Derivative of the natural logarithmic function
\(\dfrac{d}{dx}\Big(\ln g(x)\Big)=\dfrac{1}{g(x)}g′(x)\)
- Derivative of the general exponential function
\(\dfrac{d}{dx}\Big(b^{g(x)}\Big)=b^{g(x)}g′(x)\ln b\)
- Derivative of the general logarithmic function
\(\dfrac{d}{dx}\Big(\log_b g(x)\Big)=\dfrac{g′(x)}{g(x)\ln b}\)
Glossary
- logarithmic differentiation
- is a technique that allows us to differentiate a function by first taking the natural logarithm of both sides of an equation, applying properties of logarithms to simplify the equation, and differentiating implicitly


