6.2E: Exercises for Section 6.2
- Page ID
- 69809
1) Derive the formula for the volume of a sphere using the slicing method.
2) Use the slicing method to derive the formula for the volume of a cone.
3) Use the slicing method to derive the formula for the volume of a tetrahedron with side length \(a.\)
4) Use the disk method to derive the formula for the volume of a trapezoidal cylinder.
5) Explain when you would use the disk method versus the washer method. When are they interchangeable?
Volumes by Slicing
For exercises 6 - 10, draw a typical slice and find the volume using the slicing method for the given volume.
6) A pyramid with height 6 units and square base of side 2 units, as pictured here.
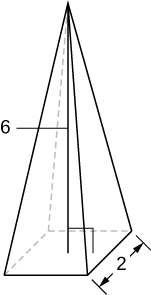
- Solution:
- Here the cross-sections are squares taken perpendicular to the \(y\)-axis.
We use the vertical cross-section of the pyramid through its center to obtain an equation relating \(x\) and \(y\).
Here this would be the equation, \( y = 6 - 6x \). Since we need the dimensions of the square at each \(y\)-level, we solve this equation for \(x\) to get, \(x = 1 - \tfrac{y}{6}\).
This is half the distance across the square cross-section at the \(y\)-level, so the side length of the square cross-section is, \(s = 2\left(1 - \tfrac{y}{6}\right).\)
Thus, we have the area of a cross-section is,
\(A(y) = \left[2\left(1 - \tfrac{y}{6}\right)\right]^2 = 4\left(1 - \tfrac{y}{6}\right)^2.\)
\(\begin{align*} \text{Then},\quad V &= \int_0^6 4\left(1 - \tfrac{y}{6}\right)^2 \, dy \\[5pt]
&= -24 \int_1^0 u^2 \, du, \quad \text{where} \, u = 1 - \tfrac{y}{6}, \, \text{so} \, du = -\tfrac{1}{6}\,dy, \quad \implies \quad -6\,du = dy \\[5pt]
&= 24 \int_0^1 u^2 \, du = 24\dfrac{u^3}{3}\bigg|_0^1 \\[5pt]
&= 8u^3\bigg|_0^1 \\[5pt]
&= 8\left( 1^3 - 0^3 \right) \quad= \quad 8\, \text{units}^3 \end{align*}\)
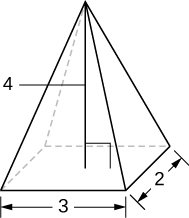
7) A pyramid with height 4 units and a rectangular base with length 2 units and width 3 units, as pictured here.
8) A tetrahedron with a base side of 4 units,as seen here.
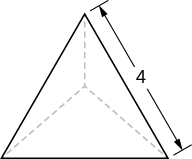
- Answer
- \(V = \frac{32}{3\sqrt{2}} = \frac{16\sqrt{2}}{3}\) units3
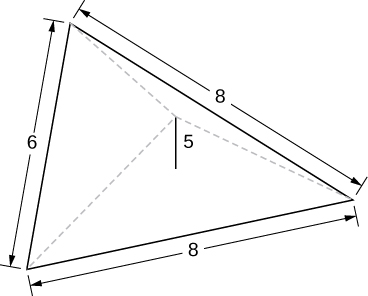
9) A pyramid with height 5 units, and an isosceles triangular base with lengths of 6 units and 8 units, as seen here.
10) A cone of radius \( r\) and height \( h\) has a smaller cone of radius \( r/2\) and height \( h/2\) removed from the top, as seen here. The resulting solid is called a frustum.
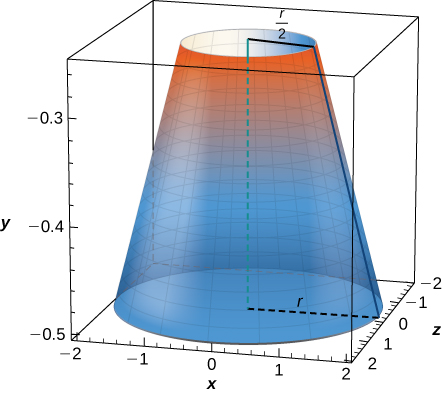
- Answer
- \(V = \frac{7\pi}{12} hr^2\) units3
For exercises 11 - 16, draw an outline of the solid and find the volume using the slicing method.
11) The base is a circle of radius \( a\). The slices perpendicular to the base are squares.
12) The base is a triangle with vertices \( (0,0),(1,0),\) and \( (0,1)\). Slices perpendicular to the \(xy\)-plane are semicircles.
- Answer
-
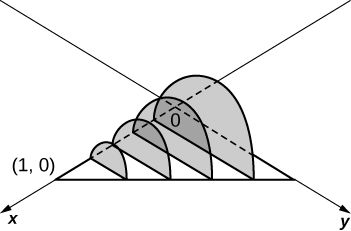
\(\displaystyle V = \int_0^1 \frac{\pi(1-x)^2}{8}\, dx \quad = \quad \frac{π}{24}\) units3
13) The base is the region under the parabola \( y=1−x^2\) in the first quadrant. Slices perpendicular to the \(xy\)-plane are squares.
14) The base is the region under the parabola \( y=1−x^2\) and above the \(x\)-axis. Slices perpendicular to the \(y\)-axis are squares.
- Answer
-
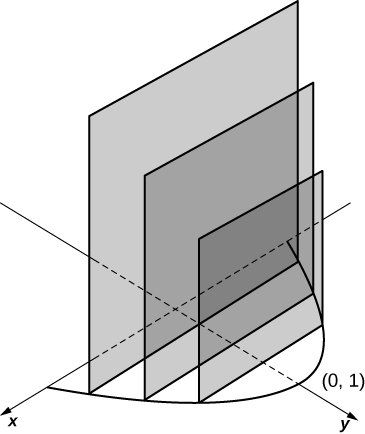
\(\displaystyle V = \int_0^1 4(1 - y)\,dy \quad = \quad 2\) units3
15) The base is the region enclosed by \( y=x^2)\) and \( y=9.\) Slices perpendicular to the \(x\)-axis are right isosceles triangles.
16) The base is the area between \( y=x\) and \( y=x^2\). Slices perpendicular to the \(x\)-axis are semicircles.
- Answer
-
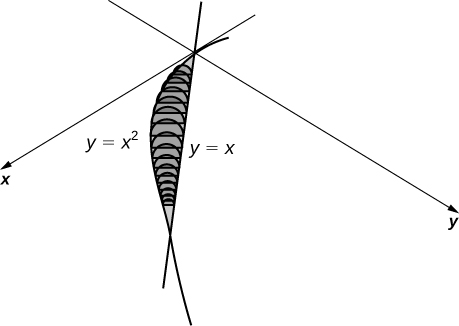
\(\displaystyle V = \int_0^1 \frac{\pi}{8}\left( x - x^2 \right)^2 \, dx \quad=\quad \frac{π}{240}\) units3
Disk and Washer Method
For exercises 17 - 24, draw the region bounded by the curves. Then, use the disk or washer method to find the volume when the region is rotated around the \(x\)-axis.
17) \( x+y=8,\quad x=0\), and \( y=0\)
18) \( y=2x^2,\quad x=0,\quad x=4,\) and \( y=0\)
- Answer
-
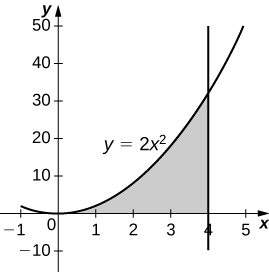
\(\displaystyle V = \int_0^4 4\pi x^4\, dx \quad=\quad \frac{4096π}{5}\) units3
19) \( y=e^x+1,\quad x=0,\quad x=1,\) and \( y=0\)
20) \( y=x^4,\quad x=0\), and \( y=1\)
- Answer
-
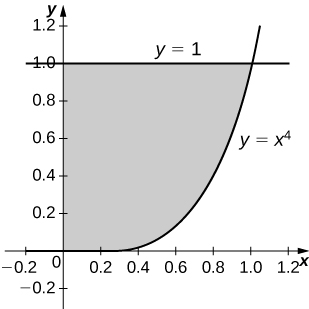
\(\displaystyle V = \int_0^1 \pi\left( 1^2 - \left( x^4\right)^2\right)\, dx = \int_0^1 \pi\left( 1 - x^8\right)\, dx \quad = \quad \frac{8π}{9}\) units3
21) \( y=\sqrt{x},\quad x=0,\quad x=4,\) and \( y=0\)
22) \( y=\sin x,\quad y=\cos x,\) and \( x=0\)
- Answer
-
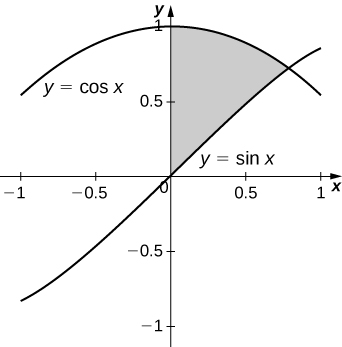
\(\displaystyle V = \int_0^{\pi/4} \pi \left( \cos^2 x - \sin^2 x\right) \, dx = \int_0^{\pi/4} \pi \cos 2x \, dx \quad=\quad \frac{π}{2}\) units3
23) \( y=\dfrac{1}{x},\quad x=2\), and \( y=3\)
24) \( x^2−y^2=9\) and \( x+y=9,\quad y=0\) and \( x=0\)
- Answer
-
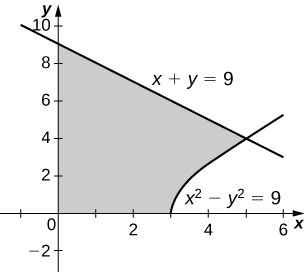
\(V = 207π\) units3
For exercises 25 - 32, draw the region bounded by the curves. Then, find the volume when the region is rotated around the \(y\)-axis.
25) \( y=4−\dfrac{1}{2}x,\quad x=0,\) and \( y=0\)
26) \( y=2x^3,\quad x=0,\quad x=1,\) and \( y=0\)
- Answer
-
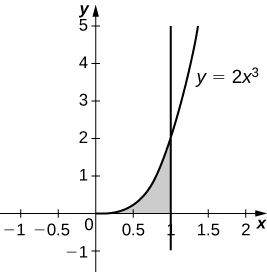
\(V = \frac{4π}{5}\) units3
27) \( y=3x^2,\quad x=0,\) and \( y=3\)
28) \( y=\sqrt{4−x^2},\quad y=0,\) and \( x=0\)
- Answer
-
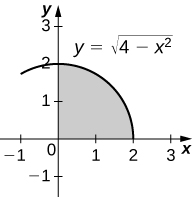
\(V = \frac{16π}{3}\) units3
29) \( y=\dfrac{1}{\sqrt{x+1}},\quad x=0\), and \( x=3\)
30) \( x=\sec(y)\) and \( y=\dfrac{π}{4},\quad y=0\) and \( x=0\)
- Answer
-
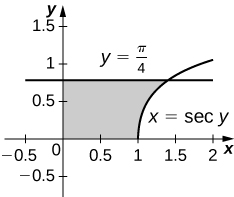
\(V = π\) units3
31) \( y=\dfrac{1}{x+1},\quad x=0\), and \( x=2\)
32) \( y=4−x,\quad y=x,\) and \( x=0\)
- Answer
-
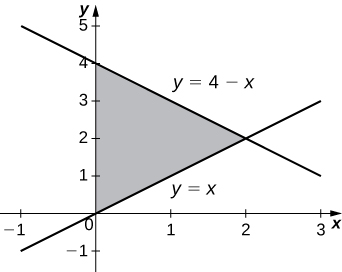
\(V = \frac{16π}{3}\) units3
For exercises 33 - 40, draw the region bounded by the curves. Then, find the volume when the region is rotated around the \(x\)-axis.
33) \( y=x+2,\quad y=x+6,\quad x=0\), and \( x=5\)
34) \( y=x^2\) and \( y=x+2\)
- Answer
-
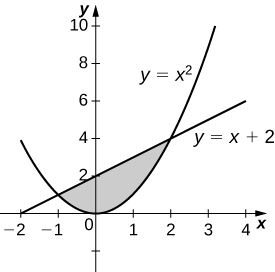
\(V = \frac{72π}{5}\) units3
35) \( x^2=y^3\) and \( x^3=y^2\)
36) \( y=4−x^2\) and \( y=2−x\)
- Answer
-
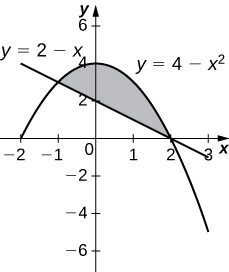
\(V = \frac{108π}{5}\) units3
37) [T] \( y=\cos x,\quad y=e^{−x},\quad x=0\), and \( x=1.2927\)
38) \( y=\sqrt{x}\) and \( y=x^2\)
- Answer
-
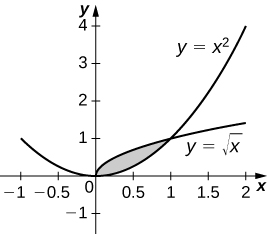
\(V = \frac{3π}{10}\) units3
39) \( y=\sin x,\quad y=5\sin x,\quad x=0\) and \( x=π\)
40) \( y=\sqrt{1+x^2}\) and \( y=\sqrt{4−x^2}\)
- Answer
-
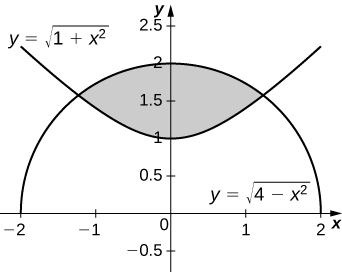
\(V = 2\sqrt{6}π\) units3
For exercises 41 - 45, draw the region bounded by the curves. Then, use the washer method to find the volume when the region is revolved around the \(y\)-axis.
41) \( y=\sqrt{x},\quad x=4\), and \( y=0\)
42) \( y=x+2,\quad y=2x−1\), and \( x=0\)
- Answer
-
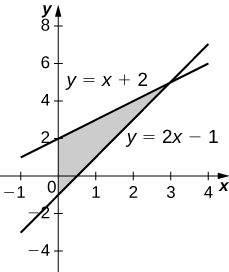
\(V = 9π\) units3
43) \( y=\dfrac{3}{x}\) and \( y=x^3\)
44) \( x=e^{2y},\quad x=y^2,\quad y=0\), and \( y=\ln(2)\)
- Answer
-
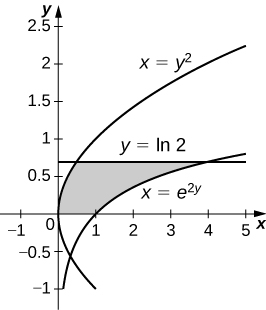
\(V = \dfrac{π}{20}(75−4\ln^5(2))\) units3
45) \( x=\sqrt{9−y^2},\quad x=e^{−y},\quad y=0\), and \( y=3\)
46) Yogurt containers can be shaped like frustums. Rotate the line \( y=\left(\frac{1}{m}\right)x\) around the \(y\)-axis to find the volume between \( y=a\) and \( y=b\).
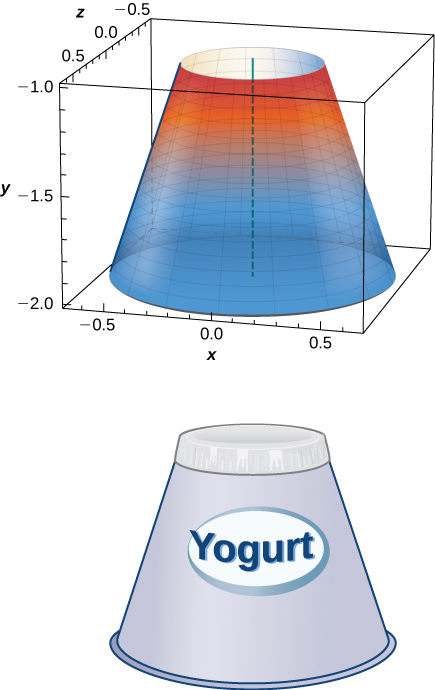
- Answer
- \(V = \dfrac{m^2π}{3}(b^3−a^3)\) units3
47) Rotate the ellipse \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) around the \(x\)-axis to approximate the volume of a football, as seen here.
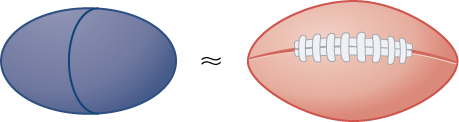
48) Rotate the ellipse \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1\) around the \(y\)-axis to approximate the volume of a football.
- Answer
- \(V = \frac{4a^2bπ}{3}\) units3
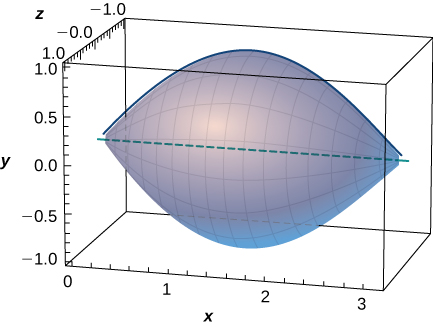
49) A better approximation of the volume of a football is given by the solid that comes from rotating \( y=\sin x) around the \(x\)-axis from \( x=0\) to \( x=π\). What is the volume of this football approximation, as seen here?
For exercises 51 - 56, find the volume of the solid described.
51) The base is the region between \( y=x\) and \( y=x^2\). Slices perpendicular to the \(x\)-axis are semicircles.
52) The base is the region enclosed by the generic ellipse \( \dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1.\) Slices perpendicular to the \(x\)-axis are semicircles.
- Answer
- \(V = \frac{2ab^2π}{3}\) units3
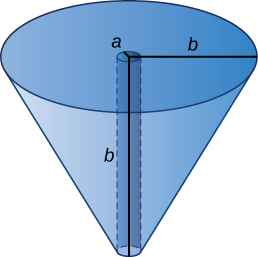
53) Bore a hole of radius a down the axis of \(a\) right cone and through the base of radius \(b\), as seen here.
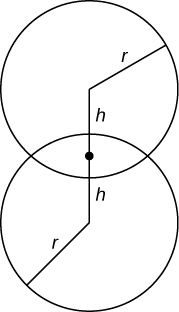
54) Find the volume common to two spheres of radius \(r\) with centers that are \(2h\) apart, as shown here.
- Answer
- \(V = \frac{π}{12}(r+h)^2(6r−h)\) units3
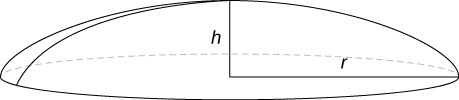
55) Find the volume of a spherical cap of height \(h\) and radius \(r\) where \(h<r\), as seen here.
56) Find the volume of a sphere of radius \(R\) with a cap of height \(h\) removed from the top, as seen here.
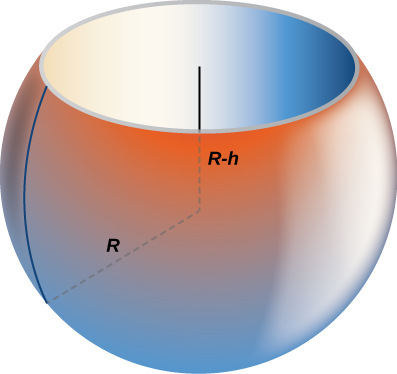
- Answer
- \(V = \dfrac{π}{3}(h+R)(h−2R)^2\) units3
Contributors
Gilbert Strang (MIT) and Edwin “Jed” Herman (Harvey Mudd) with many contributing authors. This content by OpenStax is licensed with a CC-BY-SA-NC 4.0 license. Download for free at http://cnx.org.


