8.3: Separable Equations
- Page ID
- 2558
- Use separation of variables to solve a differential equation.
- Solve applications using separation of variables.
We now examine a solution technique for finding exact solutions to a class of differential equations known as separable differential equations. These equations are common in a wide variety of disciplines, including physics, chemistry, and engineering. We illustrate a few applications at the end of the section.
Separation of Variables
We start with a definition and some examples.
A separable differential equation is any equation that can be written in the form
\[y'=f(x)g(y). \label{sep} \]
The term ‘separable’ refers to the fact that the right-hand side of Equation \ref{sep} can be separated into a function of \(x\) times a function of \(y\). Examples of separable differential equations include
\[ \begin{align} y' &=(x^2−4)(3y+2) \label{eq1} \\[4pt] y' &=6x^2+4x \label{eq2}\\[4pt] y' &=\sec y+\tan y \label{eq3} \\[4pt] y' &=xy+3x−2y−6. \label{eq4} \end{align} \]
Equation \ref{eq2} is separable with \(f(x)=6x^2+4x\) and \(g(y)=1\), Equation \ref{eq3} is separable with \(f(x)=1\) and \(g(y)=\sec y+\tan y,\) and the right-hand side of Equation \ref{eq4} can be factored as \((x+3)(y−2)\), so it is separable as well. Equation \ref{eq3} is also called an autonomous differential equation because the right-hand side of the equation is a function of \(y\) alone. If a differential equation is separable, then it is possible to solve the equation using the method of separation of variables.
- Check for any values of \(y\) that make \(g(y)=0.\) These correspond to constant solutions.
- Rewrite the differential equation in the form \[ \dfrac{dy}{g(y)}=f(x)dx. \nonumber \]
- Integrate both sides of the equation.
- Solve the resulting equation for \(y\) if possible.
- If an initial condition exists, substitute the appropriate values for \(x\) and \(y\) into the equation and solve for the constant.
Note that Step 4 states “Solve the resulting equation for \(y\) if possible.” It is not always possible to obtain \(y\) as an explicit function of \(x\). Quite often we have to be satisfied with finding y as an implicit function of \(x\).
Find a general solution to the differential equation \(y'=(x^2−4)(3y+2)\) using the method of separation of variables.
Solution
Follow the five-step method of separation of variables.
1. In this example, \(f(x)=x^2−4\) and \(g(y)=3y+2\). Setting \(g(y)=0\) gives \(y=−\dfrac{2}{3}\) as a constant solution.
2. Rewrite the differential equation in the form
\[ \dfrac{dy}{3y+2}=(x^2−4)\,dx.\nonumber \]
3. Integrate both sides of the equation:
\[ ∫\dfrac{dy}{3y+2}=∫(x^2−4)\,dx.\nonumber \]
Let \(u=3y+2\). Then \(du=3\dfrac{dy}{dx}\,dx\), so the equation becomes
\[ \dfrac{1}{3}∫\dfrac{1}{u}\,du=\dfrac{1}{3}x^3−4x+C\nonumber \]
\[ \dfrac{1}{3}\ln|u|=\dfrac{1}{3}x^3−4x+C\nonumber \]
\[ \dfrac{1}{3}\ln|3y+2|=\dfrac{1}{3}x^3−4x+C.\nonumber \]
4. To solve this equation for \(y\), first multiply both sides of the equation by \(3\).
\[ \ln|3y+2|=x^3−12x+3C\nonumber \]
Now we use some logic in dealing with the constant \(C\). Since \(C\) represents an arbitrary constant, \(3C\) also represents an arbitrary constant. If we call the second arbitrary constant \(C_1,\) where \(C_1 = 3C,\) the equation becomes
\[ \ln|3y+2|=x^3−12x+C_1.\nonumber \]
Now exponentiate both sides of the equation (i.e., make each side of the equation the exponent for the base \(e\)).
\[ \begin{align*} e^{\ln|3y+2|} &=e^{x^3−12x+C_1} \\ |3y+2| &=e^{C_1}e^{x^3−12x} \end{align*}\]
Again define a new constant \(C_2= e^{C_1}\) (note that \(C_2 > 0\)):
\[ |3y+2|=C_2e^{x^3−12x}.\nonumber \]
Because of the absolute value on the left side of the equation, this corresponds to two separate equations:
\[3y+2=C_2e^{x^3−12x}\nonumber \]
and
\[3y+2=−C_2e^{x^3−12x}.\nonumber \]
The solution to either equation can be written in the form
\[y=\dfrac{−2±C_2e^{x^3−12x}}{3}.\nonumber \]
Since \(C_2>0\), it does not matter whether we use plus or minus, so the constant can actually have either sign. Furthermore, the subscript on the constant \(C\) is entirely arbitrary, and can be dropped. Therefore the solution can be written as
\[ y=\dfrac{−2+Ce^{x^3−12x}}{3}, \text{ where }C = \pm C_2\text{ or } C = 0.\nonumber \]
Note that in writing a single general solution in this way, we are also allowing \(C\) to equal \(0\). This gives us the singular solution, \(y = -\dfrac{2}{3}\), for the given differential equation. Check that this is indeed a solution of this differential equation!
5. No initial condition is imposed, so we are finished.
Use the method of separation of variables to find a general solution to the differential equation
\[ y'=2xy+3y−4x−6. \nonumber \]
- Hint
-
First factor the right-hand side of the equation by grouping, then use the five-step strategy of separation of variables.
- Answer
-
\[ y=2+Ce^{x^2+3x} \nonumber \]
Using the method of separation of variables, solve the initial-value problem
\[ y'=(2x+3)(y^2−4),\quad y(0)=−1.\nonumber \]
Solution
Follow the five-step method of separation of variables.
1. In this example, \(f(x)=2x+3\) and \(g(y)=y^2−4\). Setting \(g(y)=0\) gives \(y=±2\) as constant solutions.
2. Divide both sides of the equation by \(y^2−4\) and multiply by \(dx\). This gives the equation
\[\dfrac{dy}{y^2−4}=(2x+3)\,dx.\nonumber \]
3. Next integrate both sides:
\[∫\dfrac{1}{y^2−4}dy=∫(2x+3)\,dx. \label{Ex2.2} \]
To evaluate the left-hand side, use the method of partial fraction decomposition. This leads to the identity
\[\dfrac{1}{y^2−4}=\dfrac{1}{4}\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right).\nonumber \]
Then Equation \ref{Ex2.2} becomes
\[\dfrac{1}{4}∫\left(\dfrac{1}{y−2}−\dfrac{1}{y+2}\right)dy=∫(2x+3)\,dx\nonumber \]
\[\dfrac{1}{4}\left (\ln|y−2|−\ln|y+2| \right)=x^2+3x+C.\nonumber \]
Multiplying both sides of this equation by \(4\) and replacing \(4C\) with \(C_1\) gives
\[\ln|y−2|−\ln|y+2|=4x^2+12x+C_1\nonumber \]
\[\ln \left|\dfrac{y−2}{y+2}\right|=4x^2+12x+C_1.\nonumber \]
4. It is possible to solve this equation for \(y.\) First exponentiate both sides of the equation and define \(C_2=e^{C_1}\):
\[\left|\dfrac{y−2}{y+2}\right|=C_2e^{4x^2+12x}.\nonumber \]
Next we can remove the absolute value and let a new constant \(C_3\) be positive, negative, or zero, i.e., \(C_3 =\pm C_2\) or \(C_3 = 0.\)
Then multiply both sides by \(y+2\).
\[y−2=C_3(y+2)e^{4x^2+12x}\nonumber \]
\[y−2=C_3ye^{4x^2+12x}+2C_3e^{4x^2+12x}.\nonumber \]
Now collect all terms involving \(y\) on one side of the equation, and solve for \(y\):
\[y−C_3ye^{4x^2+12x}=2+2C_3e^{4x^2+12x}\nonumber \]
\[y\big(1−C_3e^{4x^2+12x}\big)=2+2C_3e^{4x^2+12x}\nonumber \]
\[y=\dfrac{2+2C_3e^{4x^2+12x}}{1−C_3e^{4x^2+12x}}.\nonumber \]
5. To determine the value of \(C_3\), substitute \(x=0\) and \(y=−1\) into the general solution. Alternatively, we can put the same values into an earlier equation, namely the equation \(\dfrac{y−2}{y+2}=C_3e^{4x^2+12}\). This is much easier to solve for \(C_3\):
\[\dfrac{y−2}{y+2}=C_3e^{4x^2+12x}\nonumber \]
\[\dfrac{−1−2}{−1+2}=C_3e^{4(0)^2+12(0)}\nonumber \]
\[C_3=−3.\nonumber \]
Therefore the solution to the initial-value problem is
\[y=\dfrac{2−6e^{4x^2+12x}}{1+3e^{4x^2+12x}}.\nonumber \]
A graph of this solution appears in Figure \(\PageIndex{1}\).
![A graph of the solution over [-5, 3] for x and [-3, 2] for y. It begins as a horizontal line at y = -2 from x = -5 to just before -3, almost immediately steps up to y = 2 from just after x = -3 to just before x = 0, and almost immediately steps back down to y = -2 just after x = 0 to x = 3.](https://math.libretexts.org/@api/deki/files/7854/imageedit_2_3087334010.png?revision=1)
Find the solution to the initial-value problem
\[ 6y'=(2x+1)(y^2−2y−8) \nonumber \]
with \(y(0)=−3\) using the method of separation of variables.
- Hint
-
Follow the steps for separation of variables to solve the initial-value problem.
- Answer
-
\[ y=\dfrac{4+14e^{x^2+x}}{1−7e^{x^2+x}} \nonumber \]
Applications of Separation of Variables
Many interesting problems can be described by separable equations. We illustrate two types of problems: solution concentrations and Newton’s law of cooling.
Solution concentrations
Consider a tank being filled with a salt solution. We would like to determine the amount of salt present in the tank as a function of time. We can apply the process of separation of variables to solve this problem and similar problems involving solution concentrations.
A tank containing \(100\) L of a brine solution initially has \(4\) kg of salt dissolved in the solution. At time \(t=0\), another brine solution flows into the tank at a rate of \(2\) L/min. This brine solution contains a concentration of \(0.5\) kg/L of salt. At the same time, a stopcock is opened at the bottom of the tank, allowing the combined solution to flow out at a rate of \(2\) L/min, so that the level of liquid in the tank remains constant (Figure \(\PageIndex{2}\)). Find the amount of salt in the tank as a function of time (measured in minutes), and find the limiting amount of salt in the tank, assuming that the solution in the tank is well mixed at all times.
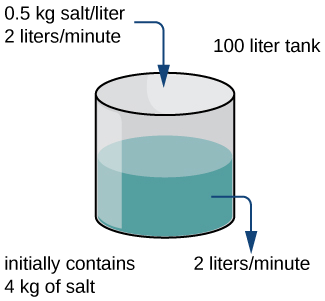
Solution
First we define a function \(u(t)\) that represents the amount of salt in kilograms in the tank as a function of time. Then \(\dfrac{du}{dt}\) represents the rate at which the amount of salt in the tank changes as a function of time. Also, \(u(0)\) represents the amount of salt in the tank at time \(t=0\), which is \(4\) kilograms.
The general setup for the differential equation we will solve is of the form
\[\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE.} \nonumber \]
INFLOW RATE represents the rate at which salt enters the tank, and OUTFLOW RATE represents the rate at which salt leaves the tank. Because solution enters the tank at a rate of \(2\) L/min, and each liter of solution contains \(0.5\) kilogram of salt, every minute \(2(0.5)=1\) kilogram of salt enters the tank. Therefore INFLOW RATE = \(1\).
To calculate the rate at which salt leaves the tank, we need the concentration of salt in the tank at any point in time. Since the actual amount of salt varies over time, so does the concentration of salt. However, the volume of the solution remains fixed at 100 liters. The number of kilograms of salt in the tank at time \(t\) is equal to \(u(t)\). Thus, the concentration of salt is \(\dfrac{u(t)}{100}\) kg/L, and the solution leaves the tank at a rate of \(2\) L/min. Therefore salt leaves the tank at a rate of \(\dfrac{u(t)}{100}⋅2=\dfrac{u(t)}{50}\) kg/min, and OUTFLOW RATE is equal to \(\dfrac{u(t)}{50}\). Therefore the differential equation becomes \(\dfrac{du}{dt}=1−\dfrac{u}{50}\), and the initial condition is \(u(0)=4.\) The initial-value problem to be solved is
\[\dfrac{du}{dt}=1−\dfrac{u}{50},u(0)=4.\nonumber \]
The differential equation is a separable equation, so we can apply the five-step strategy for solution.
Step 1. Setting \(1−\dfrac{u}{50}=0\) gives \(u=50\) as a constant solution. Since the initial amount of salt in the tank is \(4\) kilograms, this solution does not apply.
Step 2. Rewrite the equation as
\[\dfrac{du}{dt}=\dfrac{50−u}{50}.\nonumber \]
Then multiply both sides by \(dt\) and divide both sides by \(50−u:\)
\[\dfrac{du}{50−u}=\dfrac{dt}{50}.\nonumber \]
Step 3. Integrate both sides:
\[\begin{align*} ∫\dfrac{du}{50−u} &=∫\dfrac{dt}{50} \\ −\ln|50−u| &=\dfrac{t}{50}+C. \end{align*}\]
Step 4. Solve for \(u(t)\):
\[\ln|50−u|=−\dfrac{t}{50}−C\nonumber \]
\[e^{\ln|50−u|}=e^{−(t/50)−C}\nonumber \]
\[|50−u|=C_1e^{−t/50}, \text{ where } C_1 = e^{-C}.\nonumber \]
Eliminate the absolute value by allowing the constant to be positive, negative, or zero, i.e., \(C_1 = \pm e^{-C}\) or \(C_1 = 0\):
\[50−u=C_1e^{−t/50}.\nonumber \]
Finally, solve for \(u(t)\):
\[u(t)=50−C_1e^{−t/50}.\nonumber \]
Step 5. Solve for \(C_1\):
\[\begin{align*} u(0) &=50−C_1e^{−0/50} \\ 4 &=50−C_1 \\ C_1 &=46. \end{align*}\]
The solution to the initial value problem is \(u(t)=50−46e^{−t/50}.\) To find the limiting amount of salt in the tank, take the limit as \(t\) approaches infinity:
\[\begin{align*} \lim_{t→∞}u(t) &=50−46e^{−t/50} \\ &=50−46(0)=50. \end{align*}\]
Note that this was the constant solution to the differential equation. If the initial amount of salt in the tank is \(50\) kilograms, then it remains constant. If it starts at less than \(50\) kilograms, then it approaches \(50\) kilograms over time.
A tank contains \(3\) kilograms of salt dissolved in \(75\) liters of water. A salt solution of \(0.4\) kg salt/L is pumped into the tank at a rate of \(6\) L/min and is drained at the same rate. Solve for the salt concentration at time \(t\). Assume the tank is well mixed at all times.
- Hint
-
Follow the steps in Example \(\PageIndex{3}\) and determine an expression for INFLOW and OUTFLOW. Formulate an initial-value problem, and then solve it.
Initial value problem:
\[ \dfrac{du}{dt}=2.4−\dfrac{2u}{25},\, u(0)=3 \nonumber \]
- Answer
-
\[u(t)=30−27e^{−t/50} \nonumber \]
Newton’s Law of Cooling
Newton’s law of cooling states that the rate of change of an object’s temperature is proportional to the difference between its own temperature and the ambient temperature (i.e., the temperature of its surroundings). If we let \(T(t)\) represent the temperature of an object as a function of time, then \(\dfrac{dT}{dt}\) represents the rate at which that temperature changes. The temperature of the object’s surroundings can be represented by \(T_s\). Then Newton’s law of cooling can be written in the form
\[ \dfrac{dT}{dt}=k(T(t)−T_s) \nonumber \]
or simply
\[ \dfrac{dT}{dt}=k(T−T_s). \nonumber \]
The temperature of the object at the beginning of any experiment is the initial value for the initial-value problem. We call this temperature \(T_0\). Therefore the initial-value problem that needs to be solved takes the form
\[ \dfrac{dT}{dt}=k(T−T_s) \label{newton} \]
with \(T(0)=T_0\), where \(k\) is a constant that needs to be either given or determined in the context of the problem. We use these equations in Example \(\PageIndex{4}\).
A pizza is removed from the oven after baking thoroughly, and the temperature of the oven is \(350°F.\) The temperature of the kitchen is \(75°F\), and after \(5\) minutes the temperature of the pizza is \(340°F\). We would like to wait until the temperature of the pizza reaches \(300°F\) before cutting and serving it (Figure \(\PageIndex{3}\)). How much longer will we have to wait?

Solution
The ambient temperature (surrounding temperature) is \(75°F\), so \(T_s=75\). The temperature of the pizza when it comes out of the oven is \(350°F\), which is the initial temperature (i.e., initial value), so \(T_0=350\). Therefore Equation \ref{newton} becomes
\[\dfrac{dT}{dt}=k(T−75) \nonumber \]
with \(T(0)=350.\)
To solve the differential equation, we use the five-step technique for solving separable equations.
1. Setting the right-hand side equal to zero gives \(T=75\) as a constant solution. Since the pizza starts at \(350°F,\) this is not the solution we are seeking.
2. Rewrite the differential equation by multiplying both sides by \(dt\) and dividing both sides by \(T−75\):
\[\dfrac{dT}{T−75}=k\,dt. \nonumber \]
3. Integrate both sides:
\[\begin{align*} ∫\dfrac{dT}{T−75} &=∫k\,dt \\ \ln|T−75| &=kt+C.\end{align*} \nonumber \]
4. Solve for \(T\) by first exponentiating both sides:
\[\begin{align*}e^{\ln|T−75|} &=e^{kt+C} \\ |T−75| &=C_1e^{kt}, & & \text{where } C_1 = e^C. \\ T−75 &=\pm C_1e^{kt} \\ T−75 &=Ce^{kt}, & & \text{where } C = \pm C_1\text{ or } C = 0.\\ T(t) &=75+Ce^{kt}. \end{align*} \nonumber \]
5. Solve for \(C\) by using the initial condition \(T(0)=350:\)
\[\begin{align*}T(t) &=75+Ce^{kt}\\ T(0) &=75+Ce^{k(0)} \\ 350 &=75+C \\ C &=275.\end{align*} \nonumber \]
Therefore the solution to the initial-value problem is
\[T(t)=75+275e^{kt}.\nonumber \]
To determine the value of \(k\), we need to use the fact that after \(5\) minutes the temperature of the pizza is \(340°F\). Therefore \(T(5)=340.\) Substituting this information into the solution to the initial-value problem, we have
\[T(t)=75+275e^{kt}\nonumber \]
\[T(5)=340=75+275e^{5k}\nonumber \]
\[265=275e^{5k}\nonumber \]
\[e^{5k}=\dfrac{53}{55}\nonumber \]
\[\ln e^{5k}=\ln(\dfrac{53}{55})\nonumber \]
\[5k=\ln(\dfrac{53}{55})\nonumber \]
\[k=\dfrac{1}{5}\ln(\dfrac{53}{55})≈−0.007408.\nonumber \]
So now we have \(T(t)=75+275e^{−0.007048t}.\) When is the temperature \(300°F\)? Solving for \(t,\) we find
\[T(t)=75+275e^{−0.007048t}\nonumber \]
\[300=75+275e^{−0.007048t}\nonumber \]
\[225=275e^{−0.007048t}\nonumber \]
\[e^{−0.007048t}=\dfrac{9}{11}\nonumber \]
\[\ln e^{−0.007048t}=\ln\dfrac{9}{11}\nonumber \]
\[−0.007048t=\ln\dfrac{9}{11}\nonumber \]
\[t=−\dfrac{1}{0.007048}\ln\dfrac{9}{11}≈28.5.\nonumber \]
Therefore we need to wait an additional \(23.5\) minutes (after the temperature of the pizza reached \(340°F\)). That should be just enough time to finish this calculation.
A cake is removed from the oven after baking thoroughly, and the temperature of the oven is \(450°F\). The temperature of the kitchen is \(70°F\), and after \(10\) minutes the temperature of the cake is \(430°F\).
- Write the appropriate initial-value problem to describe this situation.
- Solve the initial-value problem for \(T(t)\).
- How long will it take until the temperature of the cake is within \(5°F\) of room temperature?
- Hint
-
Determine the values of \(T_s\) and \(T_0\) then use Equation \ref{newton}.
- Answer a
-
Initial-value problem \[\dfrac{dT}{dt}=k(T−70),\quad T(0)=450\nonumber \]
- Answer b
-
\[T(t)=70+380e^{kt}\nonumber \]
- Answer c
-
Approximately \(114\) minutes.
Key Concepts
- A separable differential equation is any equation that can be written in the form \(y'=f(x)g(y).\)
- The method of separation of variables is used to find the general solution to a separable differential equation.
Key Equations
- Separable differential equation
\(y′=f(x)g(y)\)
- Solution concentration
\(\dfrac{du}{dt}=\text{INFLOW RATE − OUTFLOW RATE}\)
- Newton’s law of cooling
\(\dfrac{dT}{dt}=k(T−T_s)\)
Glossary
- autonomous differential equation
- an equation in which the right-hand side is a function of \(y\) alone
- separable differential equation
- any equation that can be written in the form \(y'=f(x)g(y)\)
- separation of variables
- a method used to solve a separable differential equation


