3.2: Double Integrals Over a General Region
- Page ID
- 2243
In the previous section we got an idea of what a double integral over a rectangle represents. We can now define the double integral of a real-valued function \(f (x, y)\) over more general regions in \(\mathbb{R}^2\).
Suppose that we have a region \(R\) in the \(x y\)-plane that is bounded on the left by the vertical line \(x = a\), bounded on the right by the vertical line \(x = b\) (where \(a < b\)), bounded below by a curve \(y = g_1(x)\), and bounded above by a curve \(y = g_2(x)\), as in Figure 3.2.1(a). We will assume that \(g_1(x) \text{ and }g_2(x)\) do not intersect on the open interval \((a,b)\) (they could intersect at the endpoints \(x = a \text{ and }x = b\), though).
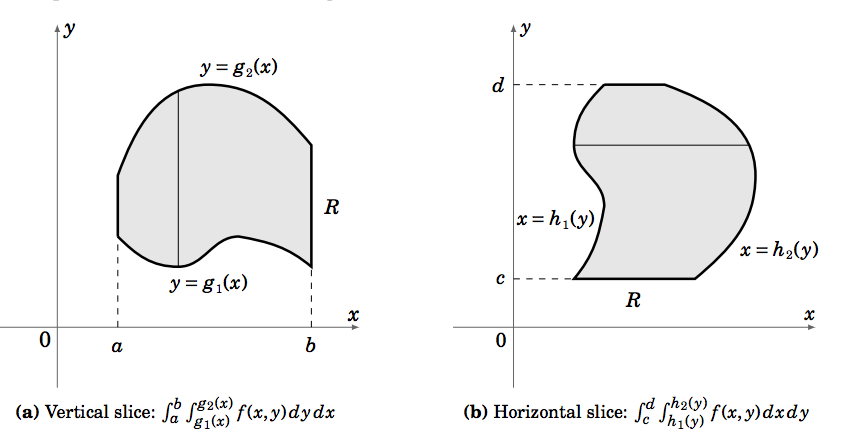
Then using the slice method from the previous section, the double integral of a real-valued function \(f (x, y)\) over the region \(R\), denoted by \(\iint\limits_R f (x, y)d A\), is given by
\[\iint\limits_R f (x, y)d A = \int_a^b \left [ \int_{g_1(x)}^{g_2(x)}f (x, y)d y \right ]dx \label{Eq3.4} \]
This means that we take vertical slices in the region \(R\) between the curves \(y = g_1(x) \text{ and }y = g_2(x)\). The symbol \(d A\) is sometimes called an area element or infinitesimal, with the \(A\) signifying area. Note that \(f (x, y)\) is first integrated with respect to \(y\), with functions of \(x\) as the limits of integration. This makes sense since the result of the first iterated integral will have to be a function of \(x\) alone, which then allows us to take the second iterated integral with respect to \(x\).
Similarly, if we have a region \(R\) in the \(x y\)-plane that is bounded on the left by a curve \(x = h_1(y)\), bounded on the right by a curve \(x = h_2(y)\), bounded below by the horizontal line \(y = c\), and bounded above by the horizontal line \(y = d\) (where \(c < d\)), as in Figure 3.2.1(b) (assuming that \(h_1(y)\text{ and }h_2(y)\) do not intersect on the open interval \((c,d)\)), then taking horizontal slices gives
\[\iint\limits_R f (x, y)d A = \int_c^d \left [ \int_{h_1(y)}^{h_2(y)}f (x, y)dx \right ]dy \label{Eq3.5}\]
Notice that these definitions include the case when the region \(R\) is a rectangle. Also, if \(f (x, y) \ge 0\) for all \((x, y)\) in the region \(R\), then \(\iint\limits_R f (x, y)d A\) is the volume under the surface \(z = f (x, y) \text{ over the region }R\).
Example 3.4
Find the volume \(V\) under the plane \(z = 8x+6y\) over the region \(R = {(x, y) : 0 ≤ x ≤ 1, 0 ≤ y ≤ 2x^2 }\).
The region \(R\) is shown in Figure 3.2.2. Using vertical slices we get:
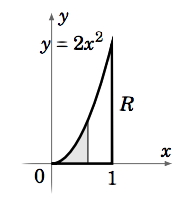
\[\nonumber \begin{align} V &=\iint\limits_R (8x+6y)d A \\[4pt] \nonumber &= \int_0^1 \left [ \int_0^{2x^2} (8x+6y)d y \right ]dx \\[4pt] \nonumber &= \int_0^1 \left (8x y+3y^2 \big |_{y=0}^{y=2x^2} \right )dx \\[4pt] \nonumber &= \int_0^1 (16x^3 +12x^4 )dx \\[4pt] \nonumber &= 4x^4 + \dfrac{12}{5} x^5 \Big |_0^1 = 4 + \dfrac{12}{5} = \dfrac{32}{5} = 6.4 \end{align}\]
We get the same answer using horizontal slices (see Figure 3.2.3):
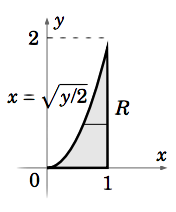
\[\nonumber \begin{align} V &=\iint\limits_R (8x+6y)d A \\[4pt] \nonumber &=\int_0^2 \left [ \int_{\sqrt{y/2}}^{1}(8x+6y)dx \right ] dy \\[4pt] \nonumber &=\int_0^2 \left (4x^2 +6x y \big |_{x=\sqrt{y/2}}^{x=1} \right )dy \\[4pt] \nonumber &= \int_0^2 (4+6y - (2y + \dfrac{6}{\sqrt{2}}y\sqrt{y}))dy = \int_0^2 (4+4y-3\sqrt{2} y^{3/2})dy \\[4pt] \nonumber &= 4y +2y^2 -\dfrac{6\sqrt{2}}{5}y^{5/2} \big |_0^2 = 8+8-\dfrac{6\sqrt{2}\sqrt{32}}{5} = 16-\dfrac{48}{5}=\dfrac{32}{5}=6.4 \end{align}\]
Example 3.5
Find the volume \(V\) of the solid bounded by the three coordinate planes and the plane \(2x+ y+4z = 4\).
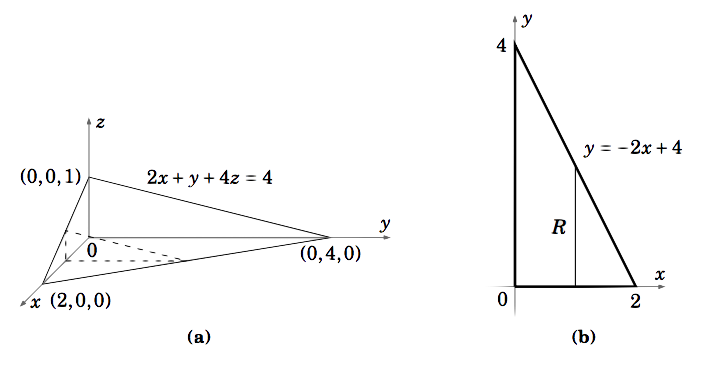
Solution
The solid is shown in Figure 3.2.4(a) with a typical vertical slice. The volume \(V\) is given by \(\iint\limits_R f (x, y)d A\), where \(f (x, y) = z = \dfrac{1}{4} (4−2x − y)\) and the region \(R\), shown in Figure 3.2.4(b), is \(R = {(x, y) : 0 ≤ x ≤ 2, 0 ≤ y ≤ −2x+4}\). Using vertical slices in \(R\) gives
\[\nonumber \begin{align} V &= \iint\limits_R \dfrac{1}{4} (4−2x− y)d A \\[4pt] \nonumber &= \int_0^2 \left [ \int_0^{-2x+4}\dfrac{1}{4} (4−2x− y)d y \right ]dx \\[4pt] \nonumber &= \int_0^2 \left ( − \dfrac{1}{8} (4−2x− y)^2 \big |_{y=0}^{y=-2x+4} \right )dx \\[4pt] \nonumber &= \int_0^2 \dfrac{1}{8}(4-2x)^2 dx \\[4pt] \nonumber &= -\dfrac{1}{48}(4-2x)^3 \big |_0^2 = \dfrac{64}{48} =\dfrac{4}{3} \end{align} \]
For a general region \(R\), which may not be one of the types of regions we have considered so far, the double integral \(\iint\limits_R f (x, y)d A\) is defined as follows. Assume that \(f (x, y)\) is a nonnegative real-valued function and that \(R\) is a bounded region in \(\mathbb{R}^2\), so it can be enclosed in some rectangle \([a,b]\times [c,d]\). Then divide that rectangle into a grid of subrectangles. Only consider the subrectangles that are enclosed completely within the region \(R\), as shown by the shaded subrectangles in Figure 3.2.5(a). In any such subrectangle \([x_i , x_{i+1}] \times [y_j , y_{j+1}]\), pick a point \((x_{i∗}, y_{j∗})\). Then the volume under the surface \(z = f (x, y)\) over that subrectangle is approximately \(f (x_{i∗}, y_{j∗})\Delta x_i \Delta y_j\), where \(\Delta x_i = x_{i+1} − x_i , \Delta y_j = y_{j+1} − y_j ,\text{ and }f (x_{i∗}, y_{j∗})\) is the height and \(\Delta x_i \Delta y_j\) is the base area of a parallelepiped, as shown in Figure 3.2.5(b). Then the total volume under the surface is approximately the sum of the volumes of all such parallelepipeds, namely
\[\sum\limits_j \sum\limits_i f (x_{i∗}, y_{j∗})\Delta x_i \Delta y_j \label{Eq3.6}\]
where the summation occurs over the indices of the subrectangles inside \(R\). If we take smaller and smaller subrectangles, so that the length of the largest diagonal of the subrectangles goes to 0, then the subrectangles begin to fill more and more of the region \(R\), and so the above sum approaches the actual volume under the surface \(z = f (x, y)\) over the region \(R\). We then define \(\iint\limits_R f (x, y)d A\) as the limit of that double summation (the limit is taken over all subdivisions of the rectangle \([a,b] \times [c,d]\) as the largest diagonal of the subrectangles goes to 0).
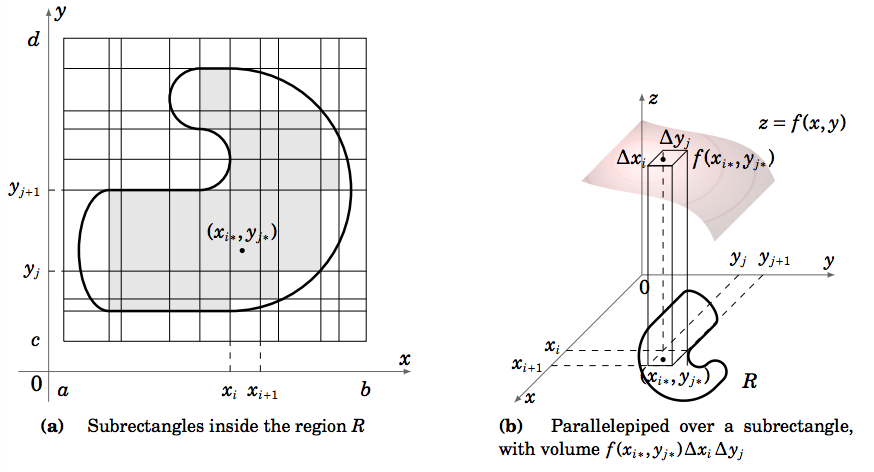
A similar definition can be made for a function \(f (x, y)\) that is not necessarily always nonnegative: just replace each mention of volume by the negative volume in the description above when \(f (x, y) < 0\). In the case of a region of the type shown in Figure 3.2.1, using the definition of the Riemann integral from single-variable calculus, our definition of \(\iint\limits_R f (x, y)d A\) reduces to a sequence of two iterated integrals.
Finally, the region \(R\) does not have to be bounded. We can evaluate improper double integrals (i.e. over an unbounded region, or over a region which contains points where the function \(f (x, y)\) is not defined) as a sequence of iterated improper single-variable integrals.
Example 3.6
Evaluate \(\int_1^{\infty}\int_0^{1/x^2} 2y d y\, dx\)
Solution
\[\nonumber \begin{align} \int_1^{\infty}\int_0^{1/x^2} 2ydy\,dx &= \int_1^{\infty} \left ( y^2 \Big |_{y=0}^{y=1/x^2} \right )dx \\[4pt] \nonumber &= \int_1^{\infty}x^{-4}dx= -\dfrac{1}{3}x^{-3} \Big |_1^{\infty} = 0-(-\dfrac{1}{3}) = \dfrac{1}{3} \end{align} \]


