11.12: Taylor's Theorem

One of the most important uses of infinite series is the potential for using an initial portion of the series for $f$ to approximate $f$. We have seen, for example, that when we add up the first $n$ terms of an alternating series with decreasing terms that the difference between this and the true value is at most the size of the next term. A similar result is true of many Taylor series.

Theorem 11.11.1: Taylor's Theorem

Suppose that $f$ is defined on some open interval $I$ around $a$ and suppose $$f^{(N+1)}(x)$$ exists on this interval. Then for each $x\not=a$ in $I$ there is a value $z$ between $x$ and $a$ so that $$f(x) = \sum_{n=0}^N {f^{(n)}(a)\over n!}\,(x-a)^n + {f^{(N+1)}(z)\over (N+1)!}(x-a)^{N+1}.$$

Proof

The proof requires some cleverness to set up, but then the details are quite elementary. We want to define a function $F(t)$. Start with the equation $$F(t)=\sum_{n=0}^N{f^{(n)}(t)\over n!}\,(x-t)^n + B(x-t)^{N+1}.$$ Here we have replaced $a$ by $t$ in the first $N+1$ terms of the Taylor series, and added a carefully chosen term on the end, with $B$ to be determined. Note that we are temporarily keeping $x$ fixed, so the only variable in this equation is $t$, and we will be interested only in $t$ between $a$ and $x$. Now substitute $t=a$: $$F(a)=\sum_{n=0}^N{f^{(n)}(a)\over n!}\,(x-a)^n + B(x-a)^{N+1}.$$ Set this equal to $f(x)$: $$f(x)=\sum_{n=0}^N{f^{(n)}(a)\over n!}\,(x-a)^n + B(x-a)^{N+1}.$$ Since $x\not=a$, we can solve this for $B$, which is a "constant''---it depends on $x$ and $a$ but those are temporarily fixed.

Now we have defined a function $F(t)$ with the property that $F(a)=f(x)$. Consider also $F(x)$: all terms with a positive power of $(x-t)$ become zero when we substitute $x$ for $t$, so we are left with $$F(x)=f^{(0)}(x)/0!=f(x).$$ So $F(t)$ is a function with the same value on the endpoints of the interval $[a,x]$. By Rolle's theorem (6.5.1), we know that there is a value $z\in(a,x)$ such that $F'(z)=0$. Let's look at $F'(t)$. Each term in $F(t)$, except the first term and the extra term involving $B$, is a product, so to take the derivative we use the product rule on each of these terms.

It will help to write out the first few terms of the definition: $$\eqalign{ F(t)=f(t)&+{f^{(1)}(t)\over 1!}(x-t)^1+{f^{(2)}(t)\over 2!}(x-t)^2+ {f^{(3)}(t)\over 3!}(x-t)^3+\cdots\cr &+{f^{(N)}(t)\over N!}(x-t)^N+ B(x-t)^{N+1}.\cr}$$ Now take the derivative: $$\eqalign{ F'(t) = f'(t) &+ \left({f^{(1)}(t)\over 1!}(x-t)^0(-1)+{f^{(2)}(t)\over 1!}(x-t)^1\right)\cr &+\left({f^{(2)}(t)\over 1!}(x-t)^1(-1)+{f^{(3)}(t)\over 2!}(x-t)^2\right)\cr &+\left({f^{(3)}(t)\over 2!}(x-t)^2(-1)+{f^{(4)}(t)\over 3!}(x-t)^3\right)+…+\cr &+\left({f^{(N)}(t)\over (N-1)!}(x-t)^{N-1}(-1)+{f^{(N+1)}(t)\over N!}(x-t)^N\right)\cr &+B(N+1)(x-t)^N(-1).\cr}$$ Now most of the terms in this expression cancel out, leaving just $$F'(t) = {f^{(N+1)}(t)\over N!}(x-t)^N+B(N+1)(x-t)^N(-1).$$ At some $z$, $F'(z)=0$ so $$\eqalign{ 0&={f^{(N+1)}(z)\over N!}(x-z)^N+B(N+1)(x-z)^N(-1)\cr B(N+1)(x-z)^N&={f^{(N+1)}(z)\over N!}(x-z)^N\cr B&={f^{(N+1)}(z)\over (N+1)!}.\cr }$$ Now we can write $$F(t)=\sum_{n=0}^N{f^{(n)}(t)\over n!}\,(x-t)^n + {f^{(N+1)}(z)\over (N+1)!}(x-t)^{N+1}.$$ Recalling that $F(a)=f(x)$ we get $$f(x)=\sum_{n=0}^N{f^{(n)}(a)\over n!}\,(x-a)^n + {f^{(N+1)}(z)\over (N+1)!}(x-a)^{N+1},$$ which is what we wanted to show.

$\square$

It may not be immediately obvious that this is particularly useful; let's look at some examples.

Example 11.11.1

Find a polynomial approximation for $\sin x$ accurate to $\pm 0.005$.

Solution

From Taylor's theorem: $$\sin x= \sum_{n=0}^N{f^{(n)}(a)\over n!}\,(x-a)^n + {f^{(N+1)}(z)\over (N+1)!}(x-a)^{N+1}.$$ What can we say about the size of the term $${f^{(N+1)}(z)\over (N+1)!}(x-a)^{N+1}?$$ Every derivative of $\sin x$ is $\pm\sin x$ or $\pm\cos x$, so $|f^{(N+1)}(z)|\le 1$. The factor $(x-a)^{N+1}$ is a bit more difficult, since $x-a$ could be quite large. Let's pick $a=0$ and $|x|\le\pi/2$; if we can compute $\sin x$ for $x\in[-\pi/2,\pi/2]$, we can of course compute $\sin x$ for all $x$.

We need to pick $N$ so that $$\left|{x^{N+1}\over (N+1)!}\right| < 0.005.$$ Since we have limited $x$ to $[-\pi/2,\pi/2]$, $$\left|{x^{N+1}\over (N+1)!}\right| < {2^{N+1}\over (N+1)!}.$$ The quantity on the right decreases with increasing $N$, so all we need to do is find an $N$ so that $${2^{N+1}\over (N+1)!} < 0.005.$$ A little trial and error shows that $N=8$ works, and in fact $2^{9}/9! < 0.0015$, so

$$\eqalign{ \sin x &=\sum_{n=0}^8{f^{(n)}(0)\over n!}\,x^n \pm 0.0015\cr &=x-{x^3\over 6}+{x^5\over 120}-{x^7\over 5040}\pm 0.0015.\cr }$$

Figure 11.11.1 shows the graphs of $\sin x$ and and the approximation on $[0,3\pi/2]$. As $x$ gets larger, the approximation heads to negative infinity very quickly, since it is essentially acting like $-x^7$.

Example 11.11.2

Figure 11.11.1. $\sin x$ and a polynomial approximation.

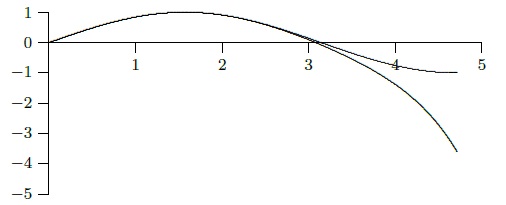
Solution

We can extract a bit more information from this example. If we do not limit the value of $x$, we still have $$\left|{f^{(N+1)}(z)\over (N+1)!}x^{N+1}\right|\le \left|{x^{N+1}\over (N+1)!}\right|$$ so that $\sin x$ is represented by

$$\sum_{n=0}^N{f^{(n)}(0)\over n!}\,x^n \pm \left|{x^{N+1}\over (N+1)!}\right|.$$

If we can show that $$\lim_{N\to\infty} \left|{x^{N+1}\over (N+1)!}\right|=0$$ for each x then

$$\sin x=\sum_{n=0}^\infty{f^{(n)}(0)\over n!}\,x^n = \sum_{n=0}^\infty (-1)^n{x^{2n+1}\over (2n+1)!},$$

that is, the sine function is actually equal to its Maclaurin series for all x. How can we prove that the limit is zero? Suppose that N is larger than $|x|$, and let M be the largest integer less than $|x|$ (if $M=0$ the following is even easier). Then

$$\eqalign{ {|x^{N+1}|\over (N+1)!} &= {|x|\over N+1}{|x|\over N}{|x|\over N-1}\cdots {|x|\over M+1}{|x|\over M}{|x|\over M-1}\cdots {|x|\over 2}{|x|\over 1}\cr &\le {|x|\over N+1}\cdot 1\cdot 1\cdots 1\cdot {|x|\over M}{|x|\over M-1}\cdots {|x|\over 2}{|x|\over 1}\cr &={|x|\over N+1}{|x|^M\over M!}. }$$

The quantity $|x|^M/ M!$ is a constant, so $$\lim_{N\to\infty} {|x|\over N+1}{|x|^M\over M!} = 0$$ and by the Squeeze Theorem (11.1.3)

$$\lim_{N\to\infty} \left|{x^{N+1}\over (N+1)!}\right|=0$$ as desired. Essentially the same argument works for $\cos x$ and $e^x$; unfortunately, it is more difficult to show that most functions are equal to their Maclaurin series.

Example 11.11.3

Find a polynomial approximation for $e^x$ near $x=2$ accurate to $\pm 0.005$.

Solution

From Taylor's theorem: $$e^x= \sum_{n=0}^N{e^2\over n!}\,(x-2)^n + {e^z\over (N+1)!}(x-2)^{N+1},$$ since $f^{(n)}(x)=e^x$ for all n. We are interested in x near 2, and we need to keep $|(x-2)^{N+1}|$ in check, so we may as well specify that $|x-2|\le 1$, so $x\in[1,3]$. Also $$\left|{e^z\over (N+1)!}\right|\le {e^3\over (N+1)!},$$ so we need to find an N that makes $e^3/(N+1)!\le 0.005$. This time $N=5$ makes $e^3/(N+1)! < 0.0015$, so the approximating polynomial is $$e^x=e^2+e^2(x-2)+{e^2\over2}(x-2)^2+{e^2\over6}(x-2)^3+ {e^2\over24}(x-2)^4+{e^2\over120}(x-2)^5 \pm 0.0015.$$ This presents an additional problem for approximation, since we also need to approximate $e^2$, and any approximation we use will increase the error, but we will not pursue this complication.

Note well that in these examples we found polynomials of a certain accuracy only on a small interval, even though the series for $\sin x$ and $e^x$ converge for all $x$; this is typical. To get the same accuracy on a larger interval would require more terms.

Contributors

• David Guichard (Whitman College)

• Integrated by Justin Marshall.