Skip to main content
Library homepage
 

Text Color

Text Size

 

Margin Size

 

Font Type

Enable Dyslexic Font
Mathematics LibreTexts

7.7: Improper Integrals

  1. CCBYNCSA
  2. Last updated
    Mar 22, 2025
  3. Save as PDF
  • Gilbert Strang & Edwin “Jed” Herman
  • OpenStax

( \newcommand{\kernel}{\mathrm{null}\,}\)

Learning Objectives
  • Evaluate an integral over an infinite interval.
  • Evaluate an integral over a closed interval with an infinite discontinuity within the interval.
  • Use the comparison theorem to determine whether a definite integral is convergent.

Is the area between the graph of and the -axis over the interval finite or infinite? If this same region is revolved about the -axis, is the volume finite or infinite? Surprisingly, the area of the region described is infinite, but the volume of the solid obtained by revolving this region about the -axis is finite.

In this section, we define integrals over an infinite interval as well as integrals of functions containing a discontinuity on the interval. Integrals of these types are called improper integrals. We examine several techniques for evaluating improper integrals, all of which involve taking limits.

Integrating over an Infinite Interval

How should we go about defining an integral of the type We can integrate for any value of , so it is reasonable to look at the behavior of this integral as we substitute larger values of . Figure shows that may be interpreted as area for various values of . In other words, we may define an improper integral as a limit, taken as one of the limits of integration increases or decreases without bound.

This figure has three graphs. All the graphs have the same curve, which is f(x). The curve is non-negative, only in the first quadrant, and decreasing. Under all three curves is a shaded region bounded by a on the x-axis an t on the x-axis. The region in the first curve is small, and progressively gets wider under the second and third graph as t moves further to the right away from a on the x-axis.
Figure : To integrate a function over an infinite interval, we consider the limit of the integral as the upper limit increases without bound.
Definition: Improper Integral
  1. Let be continuous over an interval of the form . Then provided this limit exists.
  2. Let be continuous over an interval of the form . Then provided this limit exists.

In each case, if the limit exists, then the improper integral is said to converge. If the limit does not exist, then the improper integral is said to diverge.

  1. Let be continuous over . Then provided that and both converge.
    If either of these two integrals diverge, then diverges.

(It can be shown that, in fact, for any value of a.).

In our first example, we return to the question we posed at the start of this section: Is the area between the graph of and the -axis over the interval finite or infinite?

Example : Finding an Area

Determine whether the area between the graph of and the -axis over the interval is finite or infinite.

Solution

We first do a quick sketch of the region in question, as shown in Figure .

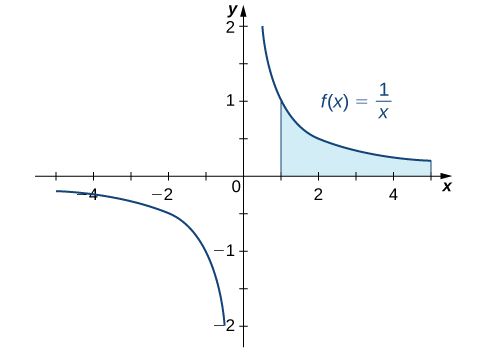
This figure is the graph of the function y = 1/x. It is a decreasing function with a vertical asymptote at the y-axis. In the first quadrant there is a shaded region under the curve bounded by x = 1 and x = 4.
Figure : We can find the area between the curve and the -axis on an infinite interval.

We can see that the area of this region is given by

which can be evaluated using Equation :

Since the improper integral diverges to the area of the region is infinite.

Example : Finding a Volume

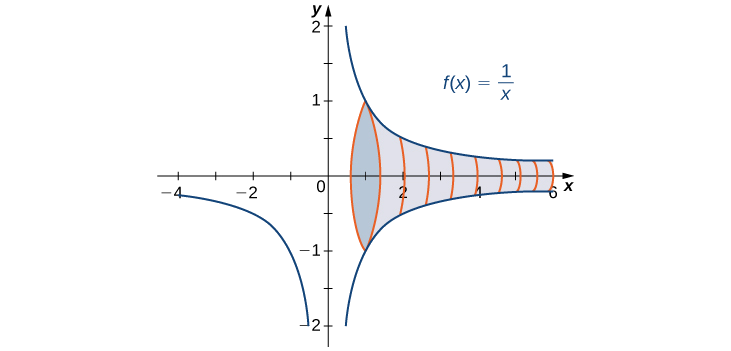
Find the volume of the solid obtained by revolving the region bounded by the graph of and the -axis over the interval about the -axis.

Solution

The solid is shown in Figure . Using the disk method, we see that the volume is

This figure is the graph of the function y = 1/x. It is a decreasing function with a vertical asymptote at the y-axis. The graph shows a solid that has been generated by rotating the curve in the first quadrant around the x-axis.
Figure : The solid of revolution can be generated by rotating an infinite area about the -axis.

Then we have

Erroneous nesting of equation structures\displaystyle \begin{align*} V &=π\int ^{+∞}_1\frac{1}{x^2}\,dx \\[4pt] &=π\lim_{t→+∞}\int ^t_1\frac{1}{x^2}\,dx & & \text{Rewrite as a limit.} \\[4pt] &=π\lim_{t→+∞}−\frac{1}{x}∣^t_1 & & \text{Find the antiderivative.} \\[4pt] &=π\lim_{t→+∞}\left(−\frac{1}{t}+1\right) & & \text{Evaluate the antiderivative.} \\[4pt] &=π\lim_{t→+∞}\left(-\cancelto{0}{\frac{1}{t}}+1\right) & & \text{Evaluate the antiderivative.} \\[4pt] &=π \end{align*}

The improper integral converges to . Therefore, the volume of the solid of revolution is .

In conclusion, although the area of the region between the -axis and the graph of over the interval is infinite, the volume of the solid generated by revolving this region about the -axis is finite. The solid generated is known as Gabriel’s Horn.

Note: Gabriel's horn (also called Torricelli's trumpet) is a geometric figure which has infinite surface area, but finite volume. The name refers to the tradition identifying the Archangel Gabriel as the angel who blows the horn to announce Judgment Day, associating the divine, or infinite, with the finite. The properties of this figure were first studied by Italian physicist and mathematician Evangelista Torricelli in the 17th century.

Example : Traffic Accidents in a City

Suppose that at a busy intersection, traffic accidents occur at an average rate of one every three months. After residents complained, changes were made to the traffic lights at the intersection. It has now been eight months since the changes were made and there have been no accidents. Were the changes effective or is the 8-month interval without an accident a result of chance?

This is a picture of a city street with a traffic signal. The picture has very busy lanes of traffic in both directions.
Figure : Modification of work by David McKelvey, Flickr.

Probability theory tells us that if the average time between events is , the probability that , the time between events, is between and is given by

where

Thus, if accidents are occurring at a rate of one every 3 months, then the probability that , the time between accidents, is between and is given by

where

To answer the question, we must compute and decide whether it is likely that 8 months could have passed without an accident if there had been no improvement in the traffic situation.

Solution

We need to calculate the probability as an improper integral:

Erroneous nesting of equation structures\displaystyle \begin{align*} P(X≥8) &=\int ^{+∞}_83e^{−3x}\,dx \\[4pt] &=\lim_{t→+∞}\int ^t_83e^{−3x}\,dx \\[4pt] &=\lim_{t→+∞}−e^{−3x}∣^t_8 \\[4pt] &=\lim_{t→+∞}(−e^{−3t}+e^{−24}) \\[4pt] &≈3.8×10^{−11}. \end{align*}

The value represents the probability of no accidents in 8 months under the initial conditions. Since this value is very, very small, it is reasonable to conclude the changes were effective.

Example : Evaluating an Improper Integral over an Infinite Interval

Evaluate State whether the improper integral converges or diverges.

Solution

Begin by rewriting as a limit using Equation from the definition. Thus,

The improper integral converges to

Example : Evaluating an Improper Integral on

Evaluate State whether the improper integral converges or diverges.

Solution

Start by splitting up the integral:

If either or diverges, then diverges.

Compute each integral separately.

For the first integral,

Erroneous nesting of equation structures\displaystyle \begin{align*} \int ^0_{−∞}xe^x\,dx &=\lim_{t→−∞}\int ^0_txe^x\,dx & & \text{Rewrite as a limit.}\\[4pt] &=\lim_{t→−∞}(xe^x−e^x)∣^0_t & & \text{Use integration by parts to find the antiderivative. (Here }u=x\text{ and }dv=e^x\,dx.\text{)} \\[4pt] &=\lim_{t→−∞}(−1−te^t+e^t) & & \text{Evaluate the antiderivative.} \\[4pt] &=−1. \end{align*}

Evaluate the limit. Note: is indeterminate of the form .Thus, by L’Hôpital’s Rule.

The first improper integral converges. For the second integral,

Erroneous nesting of equation structures\displaystyle \begin{align*} \int ^{+∞}_0xe^x\,dx &=\lim_{t→+∞}\int ^t_0xe^x\,dx & & \text{Rewrite as a limit.} \\[4pt] &=\lim_{t→+∞}(xe^x−e^x)∣^t_0 & & \text{Find the antiderivative.} \\[4pt] &=\lim_{t→+∞}(te^t−e^t+1) & & \text{Evaluate the antiderivative.} \\[4pt] &=\lim_{t→+∞}((t−1)e^t+1) & & \text{Rewrite. (}te^t−e^t\text{ is indeterminate.)} \\[4pt] &=+∞. & & \text{Evaluate the limit.} \end{align*}

Thus, diverges. Since this integral diverges, diverges as well.

Exercise

Evaluate State whether the improper integral converges or diverges.

Hint

Answer

It converges to

Integrating a Discontinuous Integrand

Now let’s examine integrals of functions containing an infinite discontinuity in the interval over which the integration occurs. Consider an integral of the form where is continuous over and discontinuous at . Since the function is continuous over for all values of satisfying , the integral is defined for all such values of . Thus, it makes sense to consider the values of as approaches for . That is, we define , provided this limit exists. Figure illustrates as areas of regions for values of approaching .

This figure has three graphs. All the graphs have the same curve, which is f(x). The curve is non-negative, only in the first quadrant, and increasing. Under all three curves is a shaded region bounded by a on the x-axis an t on the x-axis. There is also a vertical asymptote at x = b. The region in the first curve is small, and progressively gets wider under the second and third graph as t gets further from a, and closer to b on the x-axis.
Figure : As t approaches b from the left, the value of the area from a to t approaches the area from a to b.

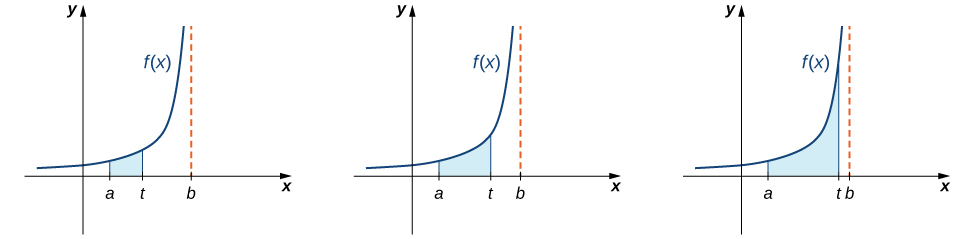
We use a similar approach to define , where is continuous over and discontinuous at . We now proceed with a formal definition.

Definition: Converging and Diverging Improper Integral
  1. Let be continuous over . Then,
  2. Let be continuous over . Then, In each case, if the limit exists, then the improper integral is said to converge. If the limit does not exist, then the improper integral is said to diverge.
  3. If is continuous over except at a point in , then provided both and converge. If either of these integrals diverges, then diverges.

The following examples demonstrate the application of this definition.

Example : Integrating a Discontinuous Integrand

Evaluate if possible. State whether the integral converges or diverges.

Solution

The function is continuous over and discontinuous at 4. Using Equation from the definition, rewrite as a limit:

Erroneous nesting of equation structures\displaystyle \begin{align*} \int ^4_0\frac{1}{\sqrt{4−x}}\,dx &=\lim_{t→4^−}\int ^t_0\frac{1}{\sqrt{4−x}}\,dx & & \text{Rewrite as a limit.} \\[4pt] &=\lim_{t→4^−}(−2\sqrt{4−x})∣^t_0 & & \text{Find the antiderivative.} \\[4pt] &=\lim_{t→4^−}(−2\sqrt{4−t}+4) & & \text{Evaluate the antiderivative.} \\[4pt] &=4. & & \text{Evaluate the limit.} \end{align*}

The improper integral converges.

Example : Integrating a Discontinuous Integrand

Evaluate State whether the integral converges or diverges.

Solution

Since is continuous over and is discontinuous at zero, we can rewrite the integral in limit form using Equation :

Erroneous nesting of equation structures\displaystyle \begin{align*} \int ^2_0x\ln x\,dx &=\lim_{t→0^+}\int ^2_tx\ln x\,dx & & \text{Rewrite as a limit.} \\[4pt] &=\lim_{t→0^+}\left(\frac{1}{2}x^2\ln x−\frac{1}{4}x^2\right)\bigg|^2_t & & \text{Evaluate}\; \int x\ln x\,dx \quad \text{using integration by parts with}\; u=\ln x\; \text{and}\; dv=x.\\[4pt] &=\lim_{t→0^+}\left(2\ln 2−1−\frac{1}{2}t^2\ln t+\frac{1}{4}t^2\right). & &\text{Evaluate the antiderivative.} \\[4pt] &=2\ln 2−1. & & \text{Evaluate the limit. Note that } \displaystyle \lim_{t→0^+}t^2\ln t\ \text{ is indeterminate.} \\[4pt] & & & \text{To evaluate it, rewrite it as a quotient and apply L’Hôpital’s rule.}\end{align*}

The improper integral converges.

Example : Integrating a Discontinuous Integrand

Evaluate State whether the improper integral converges or diverges.

Solution

Since is discontinuous at zero, using Equation , we can write

If either of the two integrals diverges, then the original integral diverges. Begin with :

Erroneous nesting of equation structures\displaystyle \begin{align*} \int ^0_{−1}\frac{1}{x^3}\,dx &=\lim_{t→0^−}\int ^t_{−1}\frac{1}{x^3}\,dx & & \text{Rewrite as a limit.} \\[4pt] &=\lim_{t→0^−}\left(−\frac{1}{2x^2}\right)\bigg|^t_{−1} & & \text{Find the antiderivative.} \\[4pt] &=\lim_{t→0^−}\left(−\frac{1}{2t^2}+\frac{1}{2}\right) & & \text{Evaluate the antiderivative.} \\[4pt] &=+∞. & & \text{Evaluate the limit.} \end{align*}

Therefore, diverges.

Since diverges, also diverges.

Exercise

Evaluate State whether the integral converges or diverges.

Hint

Write in limit form using Equation .

Answer

, It diverges.

A Comparison Theorem

It is not always easy or even possible to evaluate an improper integral directly; however, by comparing it with another carefully chosen integral, it may be possible to determine its convergence or divergence. To see this, consider two continuous functions and satisfying for (Figure ). In this case, we may view integrals of these functions over intervals of the form as areas, so we have the relationship

for .

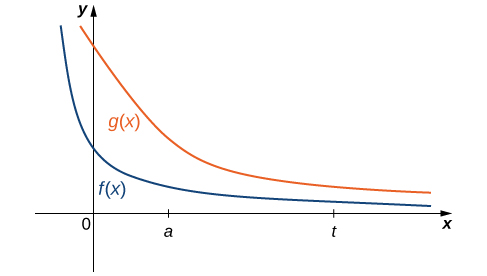
This figure has two graphs. The graphs are f(x) and g(x). The first graph f(x) is a decreasing, non-negative function with a horizontal asymptote at the x-axis. It has a sharper bend in the curve compared to g(x). The graph of g(x) is a decreasing, non-negative function with a horizontal asymptote at the x-axis.
Figure : If for , then for ,

Thus, if

then

as well. That is, if the area of the region between the graph of and the -axis over is infinite, then the area of the region between the graph of and the -axis over is infinite too.

On the other hand, if

for some real number , then

must converge to some value less than or equal to , since increases as increases and for all

If the area of the region between the graph of and the -axis over is finite, then the area of the region between the graph of and the -axis over is also finite.

These conclusions are summarized in the following theorem.

A Comparison Theorem

Let and be continuous over Assume that for

  1. If then
  2. If where is a real number, then for some real number
Example : Applying the Comparison Theorem

Use a comparison to show that

converges.

Solution

We can see that

so if converges, then so does .

To evaluate first rewrite it as a limit:

Erroneous nesting of equation structures\displaystyle \begin{align*} \int ^{+∞}_1e^{−x}\,dx &=\lim_{t→+∞}\int ^t_1e^{−x}\,dx \\[4pt] &=\lim_{t→+∞}(−e^{−x})∣^t_1  \\[4pt] &=\lim_{t→+∞}(−e^{−t}+e^{-1}) \\[4pt] &=e^{-1}. \end{align*}

Since converges, so does

Example : Applying the Comparison Theorem

Use the comparison theorem to show that diverges for all .

Solution

For over

In Example , we showed that

Therefore, diverges for all .

Exercise

Use a comparison to show that diverges.

Hint

on

Answer

Since diverges.

Laplace Transforms 

Laplace Transforms

In the last few chapters, we have looked at several ways to use integration for solving real-world problems. For this next project, we are going to explore a more advanced application of integration: integral transforms. Specifically, we describe the Laplace transform and some of its properties. The Laplace transform is used in engineering and physics to simplify the computations needed to solve some problems. It takes functions expressed in terms of time and transforms them to functions expressed in terms of frequency. It turns out that, in many cases, the computations needed to solve problems in the frequency domain are much simpler than those required in the time domain.

The Laplace transform is defined in terms of an integral as

Note that the input to a Laplace transform is a function of time, and the output is a function of frequency, . Although many real-world examples require the use of complex numbers (involving the imaginary number in this project we limit ourselves to functions of real numbers.

Let’s start with a simple example. Here we calculate the Laplace transform of . We have

This is an improper integral, so we express it in terms of a limit, which gives

Now we use integration by parts to evaluate the integral. Note that we are integrating with respect to so we treat the variable  as a constant. We have

Then we obtain

As noted above, is indeterminate of the form and requires L'Hôpital's rule to evaluate. Using L'Hôpital's rule,

  1. Calculate the Laplace transform of
  2. Calculate the Laplace transform of
  3. Calculate the Laplace transform of . (Note, you will have to integrate by parts twice.)

Laplace transforms are often used to solve differential equations. Differential equations are not covered in detail until later in this book; but, for now, let’s look at the relationship between the Laplace transform of a function and the Laplace transform of its derivative.

Let’s start with the definition of the Laplace transform. We have

Use integration by parts to evaluate . (Let and .)

After integrating by parts and evaluating the limit, you should see that

Then,

Thus, differentiation in the time domain simplifies to multiplication by in the frequency domain.

The final thing we look at in this project is how the Laplace transforms of and its antiderivative are related. Let

Then,

Use integration by parts to evaluate (Let and . Note, by the way that we have defined )

As you might expect, you should see that

Integration in the time domain simplifies to division by in the frequency domain.

Key Concepts

  • Integrals of functions over infinite intervals are defined in terms of limits.
  • Integrals of functions over an interval for which the function has a discontinuity at an endpoint may be defined in terms of limits.
  • The convergence or divergence of an improper integral may be determined by comparing it with the value of an improper integral for which the convergence or divergence is known.

Key Equations

  • Improper integrals

Glossary

improper integral
an integral over an infinite interval or an integral of a function containing an infinite discontinuity on the interval; an improper integral is defined in terms of a limit. The improper integral converges if this limit is a finite real number; otherwise, the improper integral diverges

This page titled 7.7: Improper Integrals is shared under a CC BY-NC-SA 4.0 license and was authored, remixed, and/or curated by Gilbert Strang & Edwin “Jed” Herman (OpenStax) via source content that was edited to the style and standards of the LibreTexts platform.

  1. Back to top
  • Was this article helpful?

Recommended articles

  1. 7.7: Improper IntegralsIn this section, we define integrals over an infinite interval as well as integrals of functions containing a discontinuity on the interval. Integrals...
  2. 3.7: Improper IntegralsIn this section, we define integrals over an infinite interval as well as integrals of functions containing a discontinuity on the interval. Integrals...
  3. 8.7: Improper IntegralsIn this section, we define integrals over an infinite interval as well as integrals of functions containing a discontinuity on the interval. Integrals...
  4. 8.7: Improper IntegralsIn this section, we define integrals over an infinite interval as well as integrals of functions containing a discontinuity on the interval. Integrals...
  5. 7.8: Improper IntegralsIn this section, we define integrals over an infinite interval as well as integrals of functions containing a discontinuity on the interval. Integrals...
  1. Article type
    Section or Page
    Author
    OpenStax
    License
    CC BY-NC-SA
    License Version
    4.0
    OER program or Publisher
    OpenStax
    Show Page TOC
    no
  2. Tags
    1. author@Edwin “Jed” Herman
    2. author@Gilbert Strang
    3. improper integral
    4. source@https://openstax.org/details/books/calculus-volume-1

Support Center

How can we help?