15.4: Triple Integrals
- Page ID
- 2612
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)- Recognize when a function of three variables is integrable over a rectangular box.
- Evaluate a triple integral by expressing it as an iterated integral.
- Recognize when a function of three variables is integrable over a closed and bounded region.
- Simplify a calculation by changing the order of integration of a triple integral.
- Calculate the average value of a function of three variables.
Previously, we discussed the double integral of a function \(f(x,y)\) of two variables over a rectangular region in the plane. In this section we define the triple integral of a function \(f(x,y,z)\) of three variables over a rectangular solid box in space, \(\mathbb{R}^3\). Later in this section we extend the definition to more general regions in \(\mathbb{R}^3\).
Integrable Functions of Three Variables
We can define a rectangular box \(B\) in \(\mathbb{R}^3\) as
\[B = \big\{(x,y,z)\,|\,a \leq x \leq b, \, c \leq y \leq d, \, e \leq z \leq f \big\}. \nonumber \]
We follow a similar procedure to what we did in previously. We divide the interval \([a,b]\) into \(l\) subintervals \([x_{i-1},x_i]\) of equal length \(\Delta x\) with
\[\Delta x = \dfrac{x_i - x_{i-1}}{l}, \nonumber \]
divide the interval \([c,d]\) into \(m\) subintervals \([y_{i-1}, y_i]\) of equal length \(\Delta y\) with
\[\Delta y = \dfrac{y_j - y_{j-1}}{m}, \nonumber \]
and divide the interval \([e,f]\) into \(n\) subintervals \([z_{i-1},z_i]\) of equal length \(\Delta z\) with
\[\Delta z = \dfrac{z_k - z_{k-1}}{n} \nonumber \]
Then the rectangular box \(B\) is subdivided into \(lmn\) subboxes:
\[B_{ijk} = [x_{i-1}, x_i] \times [y_{i-1}, y_i] \times [z_{i-1},z_i], \nonumber \]
as shown in Figure \(\PageIndex{1}\).
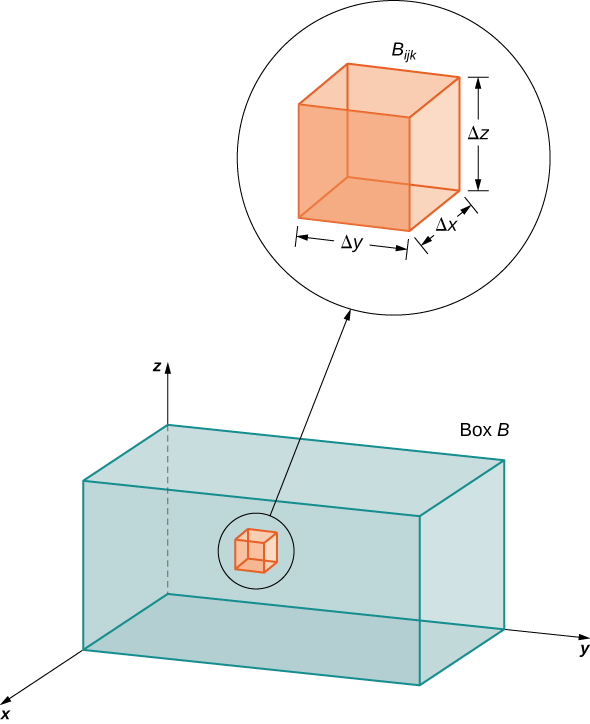
For each \(i, \, j,\) and \(k\), consider a sample point \((x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\) in each sub-box \(B_{ijk}\). We see that its volume is \(\Delta V = \Delta x \Delta y \Delta z\). Form the triple Riemann sum
\[\sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z. \nonumber \]
We define the triple integral in terms of the limit of a triple Riemann sum, as we did for the double integral in terms of a double Riemann sum.
The triple integral of a function \(f(x,y,z)\) over a rectangular box \(B\) is defined as
\[\lim_{l,m,n\rightarrow\infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f ( x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber \] if this limit exists.
When the triple integral exists on \(B\) the function \(f(x,y,z)\) is said to be integrable on \(B\). Also, the triple integral exists if \(f(x,y,z)\) is continuous on \(B\). Therefore, we will use continuous functions for our examples. However, continuity is sufficient but not necessary; in other words, \(f\) is bounded on \(B\) and continuous except possibly on the boundary of \(B\). The sample point \((x_{ijk}^*, y_{ijk}^*, z_{ijk}^*)\) can be any point in the rectangular sub-box \(B_{ijk}\) and all the properties of a double integral apply to a triple integral. Just as the double integral has many practical applications, the triple integral also has many applications, which we discuss in later sections.
Now that we have developed the concept of the triple integral, we need to know how to compute it. Just as in the case of the double integral, we can have an iterated triple integral, and consequently, a version of Fubini’s theorem for triple integrals exists.
If \(f(x,y,z)\) is continuous on a rectangular box \(B = [a,b] \times [c,d] \times [e,f]\), then
\[\iint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \,dx \, dy \, dz. \nonumber \]
This integral is also equal to any of the other five possible orderings for the iterated triple integral.
For \(a, b, c, d, e\) and \(f\) real numbers, the iterated triple integral can be expressed in six different orderings:
\[\begin{align} \int_e^f \int_c^d \int_a^b f(x,y,z)\, dx \, dy \, dz = \int_e^f \left( \int_c^d \left( \int_a^b f(x,y,z) \,dx \right) dy \right) dz \\ = \int_c^d \left( \int_e^f \left( \int_a^b f(x,y,z) \,dx \right)dz \right) dy \\ = \int_a^b \left( \int_e^f \left( \int_c^d f(x,y,z) \,dy \right)dz \right) dx \\ = \int_e^f \left( \int_a^b \left( \int_c^d f(x,y,z) \,dy \right) dx \right) dz \\ = \int_c^d \left( \int_a^b \left( \int_c^d f(x,y,z) \,dz\right)dx \right) dy \\ = \int_a^b \left( \int_c^d \left( \int_e^f f(x,y,z) \,dz \right) dy \right) dx \end{align} \nonumber \]
For a rectangular box, the order of integration does not make any significant difference in the level of difficulty in computation. We compute triple integrals using Fubini’s Theorem rather than using the Riemann sum definition. We follow the order of integration in the same way as we did for double integrals (that is, from inside to outside).
Evaluate the triple integral \[\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2)\, dx \, dy \, dz. \nonumber \]
Solution
The order of integration is specified in the problem, so integrate with respect to \(x\) first, then y, and then \(z\).
\[\begin{align*}&\int_{z=0}^{z=1} \int_{y=2}^{y=4} \int_{x=-1}^{x=5} (x + yz^2) \,dx \,dy \,dz \\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left. \left[ \dfrac{x^2}{2} + xyz^2\right|_{x=-1}^{x=5}\right]\,dy \,dz &&\text{Integrate with respect to $x$.}\\ &= \int_{z=0}^{z=1} \int_{y=2}^{y=4} \left[12+6yz^2\right] \,dy \,dz &&\text{Evaluate.}\\ &= \int_{z=0}^{z=1} \left[ \left.12y+6\dfrac{y^2}{2}z^2 \right|_{y=2}^{y=4} \right] dz &&\text{Integrate with respect to $y$.} \\ &= \int_{z=0}^{z=1} [24+36z^2] \, dz &&\text{Evaluate.} \\ &= \left[ 24z+36\dfrac{z^3}{3} \right]_{z=0}^{z=1} &&\text{Integrate with respect to $z$.}\\ &=36. &&\text{Evaluate.}\end{align*}\]
Evaluate the triple integral
\[\iiint_B x^2 yz \,dV \nonumber \]
where \(B = \big\{(x,y,z)\,|\, - 2 \leq x \leq 1, \, 0 \leq y \leq 3, \, 1 \leq z \leq 5 \big\} \) as shown in Figure \(\PageIndex{2}\).

Solution
The order is not specified, but we can use the iterated integral in any order without changing the level of difficulty. Choose, say, to integrate \(y\) first, then \(x\), and then \(z\).
\[\begin{align*}\iiint\limits_{B} x^2 yz \,dV &= \int_1^5 \int_{-2}^1 \int_0^3 [x^2 yz] \,dy \, dx \, dz \\&= \int_1^5 \int_{-2}^1 \left[ \left. x^2 \dfrac{y^2}{2} z\right|_0^3 \right] dx \, dz \\&= \int_1^5 \int_{-2}^1 \dfrac{9}{2} x^2 z \,dx \, dz \\&= \int_1^5 \left[ \left. \dfrac{9}{2} \dfrac{x^3}{3} z \right|_{-2}^1 \right] dz \\&= \int_1^5 \dfrac{27}{2} z \, dz \\&= \left. \dfrac{27}{2} \dfrac{z^2}{2} \right|_1^5 = \frac{27}{4}(25 - 1) = 162.\end{align*}\]
Now try to integrate in a different order just to see that we get the same answer. Choose to integrate with respect to \(x\) first, then \(z\), then \(y\)
\[\begin{align*}\iiint\limits_{B} x^2yz \,dV &= \int_0^3 \int_1^5 \int_{-2}^1 [x^2yz] \,dx\, dz\, dy \\&= \int_0^3 \int_1^5 \left[ \left. \dfrac{x^3}{3} yz \right|_{-2}^1 \right] dz \,dy \\&= \int_0^3 \int_1^5 3yz \; dz \,dy \\&= \int_0^3 \left.\left[ 3y\dfrac{z^2}{2} \right|_1^5 \right] \,dy \\&= \int_0^3 36y \; dy \\&= \left. 36\dfrac{y^2}{2} \right|_0^3 =18(9-0) =162.\end{align*}\]
Evaluate the triple integral
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV\nonumber \]
where \(B = \big\{(x,y,z)\,|\,0 \leq x \leq \pi, \, \dfrac{3\pi}{2} \leq y \leq 2\pi, \, 1 \leq z \leq 3 \big\}\).
- Hint
-
Follow the steps in the previous example.
- Answer
-
\[\iiint_B z \, \sin \, x \, \cos \, y \, dV = 8 \nonumber \]
The triple integral of a continuous function \(f(x,y,z)\) over a general three-dimensional region
\[E = \big\{(x,y,z)\,|\,(x,y) \in D, \, u_1(x,y) \leq z \leq u_2(x,y) \big\} \nonumber \]
in \(\mathbb{R}^3\), where \(D\) is the projection of \(E\) onto the \(xy\)-plane, is
\[\iiint_E f(x,y,z) \,dV = \iint_D \left[\int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \right] \, dA. \nonumber \]
Similarly, we can consider a general bounded region \(D\) in the \(xy\)-plane and two functions \(y = u_1(x,z)\) and \(y = u_2(x,z)\) such that \(u_1(x,z) \leq u_2(x,z)\) for all \((x,z)\) in \(D\). Then we can describe the solid region \(E\) in \(\mathbb{R}^3\) as
\[E = \big\{(x,y,z)\,|\,(x,z) \in D, \, u_1(x,z) \leq z \leq u_2(x,z) \big\} \nonumber \] where \(D\) is the projection of \(E\) onto the \(xy\)-plane and the triple integral is
\[\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(x,z)}^{u_2(x,z)} f(x,y,z) \,dy \right] \, dA. \nonumber \]
Finally, if \(D\) is a general bounded region in the \(xy\)-plane and we have two functions \(x = u_1(y,z)\) and \(x = u_2(y,z)\) such that \(u_1(y,z) \leq u_2(y,z)\) for all \((y,z)\) in \(D\), then the solid region \(E\) in \(\mathbb{R}^3\) can be described as
\[E = \big\{(x,y,z)\,|\,(y,z) \in D, \, u_1(y,z) \leq z \leq u_2(y,z) \big\} \nonumber \] where \(D\) is the projection of \(E\) onto the \(xy\)-plane and the triple integral is
\[\iiint_E f(x,y,z)\,dV = \iint_D \left[\int_{u_1(y,z)}^{u_2(y,z)} f(x,y,z) \, dx \right] \, dA. \nonumber \]
Note that the region \(D\) in any of the planes may be of Type I or Type II as described in previously. If \(D\) in the \(xy\)-plane is of Type I (Figure \(\PageIndex{4}\)), then
\[E = \big\{(x,y,z)\,|\,a \leq x \leq b, \, g_1(x) \leq y \leq g_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
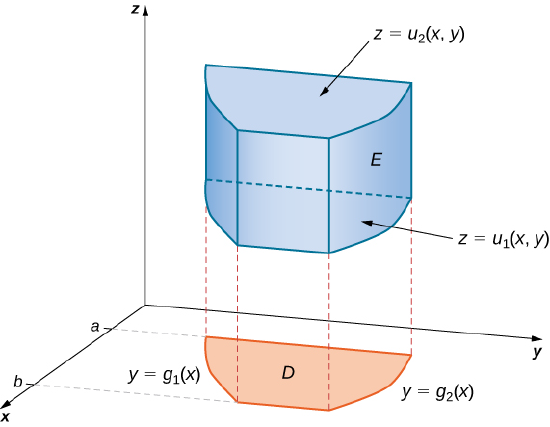
Then the triple integral becomes
\[\iiint_E f(x,y,z) \,dV = \int_a^b \int_{g_1(x)}^{g_2(x)} \int_{u_1(x,y)}^{u_2(x,y)} f(x,y,z) \,dz \, dy \, dx. \nonumber \]
If \(D\) in the \(xy\)-plane is of Type II (Figure \(\PageIndex{5}\)), then
\[E = \big\{(x,y,z)\,|\,c \leq x \leq d, h_1(x) \leq y \leq h_2(x), \, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
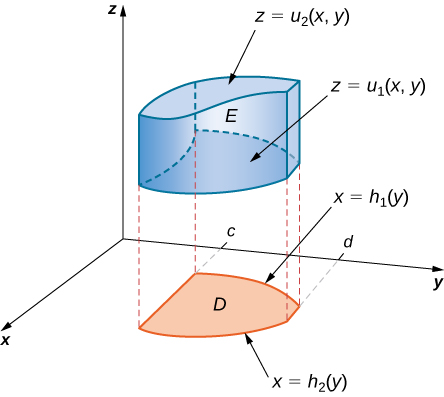
Then the triple integral becomes
\[\iiint_E f(x,y,z) \,dV = \int_{y=c}^{y=d} \int_{x=h_1(y)}^{x=h_2(y)} \int_{z=u_1(x,y)}^{z=u_2(x,y)} f(x,y,z)\,dz \, dx \, dy. \nonumber \]
Evaluate the triple integral of the function \(f(x,y,z) = 5x - 3y\) over the solid tetrahedron bounded by the planes \(x = 0, \, y = 0, \, z = 0\), and \(x + y + z = 1\).
Solution
Figure \(\PageIndex{6}\) shows the solid tetrahedron \(E\) and its projection \(D\) on the \(xy\)-plane.
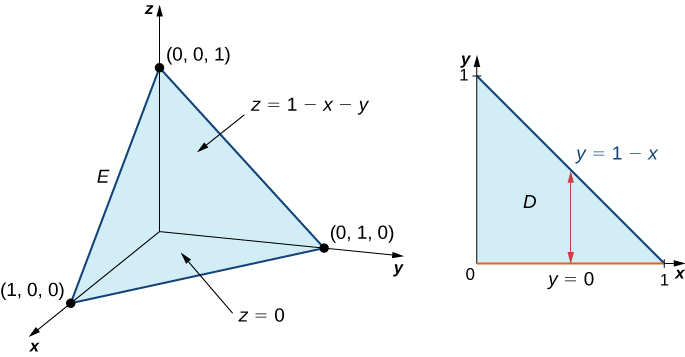
We can describe the solid region tetrahedron as
\[E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}. \nonumber \]
Hence, the triple integral is
\[\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz \, dy \, dx. \nonumber \]
To simplify the calculation, first evaluate the integral \(\displaystyle \int_{z=0}^{z=1-x-y} (5x - 3y) \,dz\). We have
\[\int_{z=0}^{z=1-x-y} (5x - 3y) \,dz = (5x - 3y)z \bigg|_{z=0}^{z=1-x-y} = (5x - 3y)(1 - x - y).\nonumber \]
Now evaluate the integral
\[\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y) \,dy, \nonumber \]
obtaining
\[\int_{y=0}^{y=1-x} (5x - 3y)(1 - x - y)\,dy = \dfrac{1}{2}(x - 1)^2 (6x - 1).\nonumber \]
Finally evaluate
\[\int_{x=0}^{x=1} \dfrac{1}{2}(x - 1)^2 (6x - 1)\,dx = \dfrac{1}{12}.\nonumber \]
Putting it all together, we have
\[\iiint_E f(x,y,z)\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y}(5x - 3y)\,dz \, dy \, dx = \dfrac{1}{12}.\nonumber \]
Just as we used the double integral \[\iint_D 1 \,dA \nonumber \] to find the area of a general bounded region \(D\) we can use \[\iiint_E 1\,dV \nonumber \] to find the volume of a general solid bounded region \(E\). The next example illustrates the method.
Find the volume of a right pyramid that has the square base in the \(xy\)-plane \([-1,1] \times [-1,1]\) and vertex at the point \((0, 0, 1)\) as shown in the following figure.
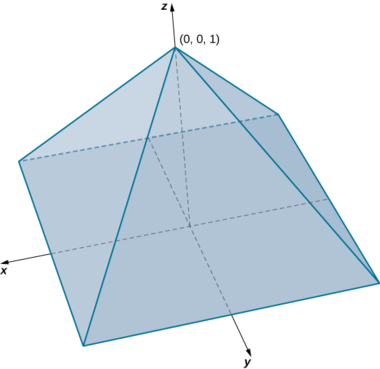
Solution
In this pyramid the value of \(z\) changes from 0 to 1 and at each height \(z\) the cross section of the pyramid for any value of \(z\) is the square
\[[-1 + z, \, 1 - z] \times [-1 + z, \, 1 - z].\nonumber \]
Hence, the volume of the pyramid is \[\iiint_E 1\,dV\nonumber \] where
\[E = \big\{(x,y,z)\,|\,0 \leq z \leq 1, \, -1 + z \leq y \leq 1 - z, \, -1 + z \leq x \leq 1 - z \big\}.\nonumber \]
Thus, we have
\[\begin{align*} \iiint_E 1\,dV &= \int_{z=0}^{z=1} \int_{y=-1+z}^{y=1-z} \int_{x=-1+z}^{x=1-z} 1\,dx \, dy \, dz \\[5pt]
&= \int_{z=0}^{z=1} \int_{y=-1+z}^{y=1-z} (2 - 2z)\, dy \, dz \\[5pt]
&= \int_{z=0}^{z=1}(2 - 2z)^2 \,dz = \dfrac{4}{3}. \end{align*}\]
Hence, the volume of the pyramid is \(\dfrac{4}{3}\) cubic units.
Consider the solid sphere \(E = \big\{(x,y,z)\,|\,x^2 + y^2 + z^2 = 9 \big\}\). Write the triple integral \[\iiint_E f(x,y,z) \,dV\nonumber \] for an arbitrary function \(f\) as an iterated integral. Then evaluate this triple integral with \(f(x,y,z) = 1\). Notice that this gives the volume of a sphere using a triple integral.
- Hint
-
Follow the steps in the previous example. Use symmetry.
- Answer
-
\[\begin{align*} \iiint_E 1\,dV = 8 \int_{x=-3}^{x=3} \int_{y=-\sqrt{9-z^2}}^{y=\sqrt{9-z^2}}\int_{z=-\sqrt{9-x^2-y^2}}^{z=\sqrt{9-x^2-y^2}} 1\,dz \, dy \, dx \\ = 36 \pi \,\text{cubic units}. \end{align*}\]
Changing the Order of Integration
As we have already seen in double integrals over general bounded regions, changing the order of the integration is done quite often to simplify the computation. With a triple integral over a rectangular box, the order of integration does not change the level of difficulty of the calculation. However, with a triple integral over a general bounded region, choosing an appropriate order of integration can simplify the computation quite a bit. Sometimes making the change to polar coordinates can also be very helpful. We demonstrate two examples here.
Consider the iterated integral
\[\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=y} f(x,y,z)\,dz \, dy \, dx. \nonumber \]
The order of integration here is first with respect to z, then y, and then x. Express this integral by changing the order of integration to be first with respect to \(x\), then \(z\), and then \(y\). Verify that the value of the integral is the same if we let \(f (x,y,z) =xyz\).
Solution
The best way to do this is to sketch the region \(E\) and its projections onto each of the three coordinate planes. Thus, let
\[E = \big\{(x,y,z)\,|\,0 \leq x \leq 1, \, 0 \leq y \leq x^2, \, 0 \leq z \leq y \big\}.\nonumber \]
and
\[\int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=x^2} f(x,y,z) \,dz \, dy \, dx = \iiint_E f(x,y,z)\,dV.\nonumber \]
We need to express this triple integral as
\[\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy.\nonumber \]
Knowing the region \(E\) we can draw the following projections (Figure \(\PageIndex{8}\)):
on the \(xy\)-plane is \(D_1 = \big\{(x,y)\,|\, 0 \leq x \leq 1, \, 0 \leq y \leq x^2 \big\} = \{ (x,y) \,|\, 0 \leq y \leq 1, \, \sqrt{y} \leq x \leq 1 \big\},\)
on the \(yz\)-plane is \(D_2 = \big\{(y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2 \big\}\), and
on the \(xz\)-plane is \(D_3 = \big\{(x,z) \,|\, 0 \leq x \leq 1, \, 0 \leq z \leq x^2 \big\}\).
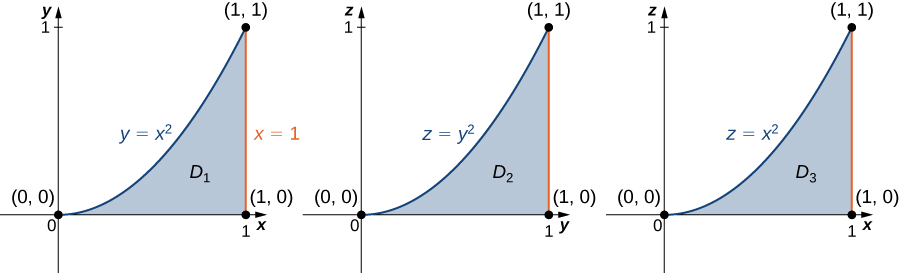
Now we can describe the same region \(E\) as \(\big\{(x,y,z) \,|\, 0 \leq y \leq 1, \, 0 \leq z \leq y^2, \, \sqrt{y} \leq x \leq 1 \big\}\), and consequently, the triple integral becomes
\[\int_{y=c}^{y=d} \int_{z=v_1(y)}^{z=v_2(y)} \int_{x=u_1(y,z)}^{x=u_2(y,z)} f(x,y,z)\,dx \, dz \, dy = \int_{y=0}^{y=1} \int_{z=0}^{z=x^2} \int_{x=\sqrt{y}}^{x=1} f(x,y,z)\,dx \, dz \, dy \nonumber \]
Now assume that \(f (x,y,z) = xyz\) in each of the integrals. Then we have
\[\begin{align*} \int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \int_{z=0}^{z=y^2} xyz \, dz \, dy \, dx &= \int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \left. \left[xy \dfrac{z^2}{2} \right|_{z=0}^{z=y^2} \right] \, dy \, dx \\[5pt]
&= \int_{x=0}^{x=1} \int_{y=0}^{y=x^2} \left( x \dfrac{y^5}{2}\right) dy \, dx \\[5pt]
&= \int_{x=0}^{x=1} \left. \left[ x\dfrac{y^6}{12} \right|_{y=0}^{y=x^2}\right] dx \\[5pt]
&= \int_{x=0}^{x=1} \dfrac{x^{13}}{12} dx = \left. \dfrac{x^{14}}{168}\right|_{x=0}^{x=1} \\[5pt]
&= \dfrac{1}{168}, \end{align*}\]
\[ \begin{align*} \int_{y=0}^{y=1} \int_{z=0}^{z=y^2} \int_{x=\sqrt{y}}^{x=1} xyz \, dx \, dz \, dy &= \int_{y=0}^{y=1} \int_{z=0}^{z=y^2} \left.\left[yz \dfrac{x^2}{2} \right|_{\sqrt{y}}^{1} \right] dz \, dy \\[5pt]
&= \int_{y=0}^{y=1} \int_{z=0}^{z=y^2} \left( \dfrac{yz}{2} - \dfrac{y^2z}{2} \right) dz \, dy \\[5pt]
&= \int_{y=0}^{y=1} \left. \left[ \dfrac{yz^2}{4} - \dfrac{y^2z^2}{4} \right|_{z=0}^{z=y^2} \right] dy \\[5pt]
&= \int_{y=0}^{y=1} \left(\dfrac{y^5}{4} - \dfrac{y^6}{4} \right) dy \\[5pt]
&= \left. \left(\dfrac{y^6}{24} - \dfrac{y^7}{28} \right) \right|_{y=0}^{y=1} \\[5pt]
&= \dfrac{1}{168}. \end{align*} \nonumber \]
The answers match.
Write five different iterated integrals equal to the given integral
\[\int_{z=0}^{z=4} \int_{y=0}^{y=4-z} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \, dx \, dy \, dz.\nonumber \]
- Hint
-
Follow the steps in the previous example, using the region \(E\) as \( \big\{(x,y,z) \,|\, 0 \leq z \leq 4, \, 0 \leq y \leq 4 - z, \, 0 \leq x \leq \sqrt{y} \big\}\), and describe and sketch the projections onto each of the three planes, five different times.
- Answer
-
\[(i) \, \int_{z=0}^{z=4} \int_{x=0}^{x=\sqrt{4-z}} \int_{y=x^2}^{y=4-z} f(x,y,z) \, dy \, dx \, dz, \, (ii) \, \int_{y=0}^{y=4} \int_{z=0}^{z=4-y} \int_{x=0}^{x=\sqrt{y}} f(x,y,z) \,dx \, dz \, dy, \,(iii) \, \int_{y=0}^{y=4} \int_{x=0}^{x=\sqrt{y}} \int_{z=0}^{Z=4-y} f(x,y,z) \,dz \, dx \, dy, \, \nonumber \]
\[ (iv) \, \int_{x=0}^{x=2} \int_{y=x^2}^{y=4} \int_{z=0}^{z=4-y} f(x,y,z) \,dz \, dy \, dx, \, (v) \int_{x=0}^{x=2} \int_{z=0}^{z=4-x^2} \int_{y=x^2}^{y=4-z} f(x,y,z) \,dy \, dz \, dx \nonumber \]
Evaluate the triple integral
\[\iiint_{E} \sqrt{x^2 + z^2} \,dV, \nonumber \]
where \(E\) is the region bounded by the paraboloid \(y = x^2 + z^2\) (Figure \(\PageIndex{9}\)) and the plane \(y = 4\).
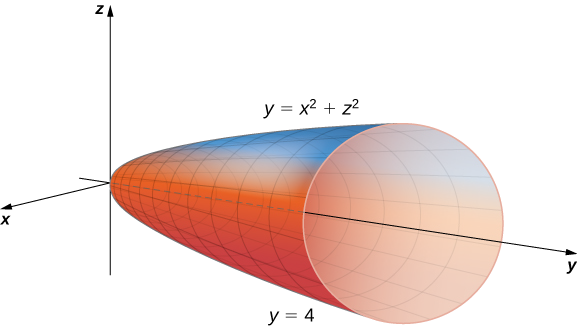
Solution
The projection of the solid region \(E\) onto the \(xy\)-plane is the region bounded above by \(y = 4\) and below by the parabola \(y = x^2\) as shown.
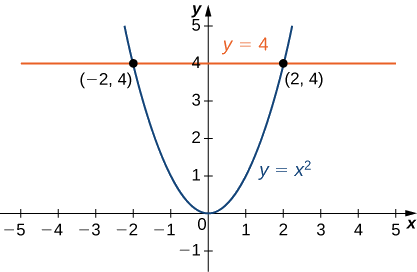
Thus, we have
\[E = \big\{(x,y,z) \,|\, -2 \leq x \leq 2, \, x^2 \leq y \leq 4, \, -\sqrt{y - x^2} \leq z \leq \sqrt{y - x^2} \big\}.\nonumber \]
The triple integral becomes
\[\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx.\nonumber \]
This expression is difficult to compute, so consider the projection of \(E\) onto the \(xz\)-plane. This is a circular disc \(x^2 + z^2 \leq 4\). So we obtain
\[\iiint_E \sqrt{x^2 + z^2} \,dV = \int_{x=-2}^{x=2} \int_{y=x^2}^{y=4} \int_{z=-\sqrt{y-x^2}}^{z=\sqrt{y-x^2}} \sqrt{x^2 + z^2} \,dz \, dy \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx.\nonumber \]
Here the order of integration changes from being first with respect to \(z\) then \(y\) and then \(x\) to being first with respect to \(y\) then to \(z\) and then to \(x\). It will soon be clear how this change can be beneficial for computation. We have
\[\int_{x=-2}^{x=2} \int_{z=\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} \int_{y=x^2+z^2}^{y=4} \sqrt{x^2 + z^2} \,dy \, dz \, dx = \int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2} \,dz \, dx.\nonumber \]
Now use the polar substitution \(x = r \, \cos \, \theta, \, z = r \, \sin \, \theta\), and \(dz \, dx = r \, dr \, d\theta\) in the \(xz\)-plane. This is essentially the same thing as when we used polar coordinates in the \(xy\)-plane, except we are replacing \(y\) by \(z\). Consequently the limits of integration change and we have, by using \(r^2 = x^2 + z^2\),
\[\int_{x=-2}^{x=2} \int_{z=-\sqrt{4-x^2}}^{z=\sqrt{4-x^2}} (4 - x^2 - z^2) \sqrt{x^2 + z^2}\,dz \, dx = \int_{\theta=0}^{\theta=2\pi} \int_{r=0}^{r=2} (4 - r^2) rr \, dr \, d\theta = \int_0^{2\pi} \left. \left[ \dfrac{4r^3}{3} - \dfrac{r^5}{5} \right|_0^2 \right] \, d\theta = \int_0^{2\pi} \dfrac{64}{15} \,d\theta = \dfrac{128\pi}{15}\nonumber \]
Average Value of a Function of Three Variables
Recall that we found the average value of a function of two variables by evaluating the double integral over a region on the plane and then dividing by the area of the region. Similarly, we can find the average value of a function in three variables by evaluating the triple integral over a solid region and then dividing by the volume of the solid.
If \(f(x,y,z)\) is integrable over a solid bounded region \(E\) with positive volume \(V \, (E),\) then the average value of the function is
\[f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \, dV. \nonumber \]
Note that the volume is
\[V \, (E) = \iiint_E 1 \,dV. \nonumber \]
The temperature at a point \((x,y,z)\) of a solid \(E\) bounded by the coordinate planes and the plane \(x + y + z = 1\) is \(T(x,y,z) = (xy + 8z + 20) \, \text{°}\text{C} \). Find the average temperature over the solid.
Solution
Use the theorem given above and the triple integral to find the numerator and the denominator. Then do the division. Notice that the plane \(x + y + z = 1\) has intercepts \((1,0,0), \, (0,1,0),\) and \((0,0,1)\). The region \(E\) looks like
\[E = \big\{(x,y,z) \,|\, 0 \leq x \leq 1, \, 0 \leq y \leq 1 - x, \, 0 \leq z \leq 1 - x - y \big\}.\nonumber \]
Hence the triple integral of the temperature is
\[\iiint_E f(x,y,z) \,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} (xy + 8z + 20) \, dz \, dy \, dx = \dfrac{147}{40}. \nonumber \]
The volume evaluation is
\[V \, (E) = \iiint_E 1\,dV = \int_{x=0}^{x=1} \int_{y=0}^{y=1-x} \int_{z=0}^{z=1-x-y} 1 \,dz \, dy \, dx = \dfrac{1}{6}. \nonumber \]
Hence the average value is
\[ T_{ave} = \dfrac{147/40}{1/6} = \dfrac{6(147)}{40} = \dfrac{441}{20} \, \text{°}\text{C} \nonumber \].
Find the average value of the function \(f(x,y,z) = xyz\) over the cube with sides of length 4 units in the first octant with one vertex at the origin and edges parallel to the coordinate axes.
- Hint
-
Follow the steps in the previous example.
- Answer
-
\(f_{ave} = 8\)
Key Concepts
- To compute a triple integral we use Fubini’s theorem, which states that if \(f(x,y,z)\) is continuous on a rectangular box \(B = [a,b] \times [c,d] \times [e,f]\), then \[\iiint_B f(x,y,z) \,dV = \int_e^f \int_c^d \int_a^b f(x,y,z) \, dx \, dy \, dz \nonumber \] and is also equal to any of the other five possible orderings for the iterated triple integral.
- To compute the volume of a general solid bounded region \(E\) we use the triple integral \[V \, (E) = \iiint_E 1 \,dV. \nonumber \]
- Interchanging the order of the iterated integrals does not change the answer. As a matter of fact, interchanging the order of integration can help simplify the computation.
- To compute the average value of a function over a general three-dimensional region, we use \[f_{ave} = \dfrac{1}{V \, (E)} \iiint_E f(x,y,z) \,dV. \nonumber \]
Key Equations
- Triple integral
\[\lim_{l,m,n \rightarrow \infty} \sum_{i=1}^l \sum_{j=1}^m \sum_{k=1}^n f(x_{ijk}^*, y_{ijk}^*, z_{ijk}^*) \,\Delta x \Delta y \Delta z = \iiint_B f(x,y,z) \,dV \nonumber \]
Glossary
- triple integral
- the triple integral of a continuous function \(f(x,y,z)\) over a rectangular solid box \(B\) is the limit of a Riemann sum for a function of three variables, if this limit exists



Triple Integrals over a General Bounded Region
We now expand the definition of the triple integral to compute a triple integral over a more general bounded region \(E\) in \(\mathbb{R}^3\). The general bounded regions we will consider are of three types. First, let \(D\) be the bounded region that is a projection of \(E\) onto the \(xy\)-plane. Suppose the region \(E\) in \(\mathbb{R}^3\) has the form
\[E = \big\{(x,y,z)\,|\,(x,y) \in D, u_1(x,y) \leq z \leq u_2(x,y) \big\}. \nonumber \]
For two functions \(z = u_1(x,y)\) and \(u_2(x,y)\), such that \(u_1(x,y) \leq u_2(x,y)\) for all \((x,y)\) in \(D\) as shown in the following figure.