17.1: Second-Order Linear Equations

Learning Objectives

• Recognize homogeneous and nonhomogeneous linear differential equations.
• Determine the characteristic equation of a homogeneous linear equation.
• Use the roots of the characteristic equation to find the solution to a homogeneous linear equation.
• Solve initial-value and boundary-value problems involving linear differential equations.

When working with differential equations, usually the goal is to find a solution. In other words, we want to find a function (or functions) that satisfies the differential equation. The technique we use to find these solutions varies, depending on the form of the differential equation with which we are working. Second-order differential equations have several important characteristics that can help us determine which solution method to use. In this section, we examine some of these characteristics and the associated terminology.

Homogeneous Linear Equations

Consider the second-order differential equation

$$xy''+2x^2y'+5x^3y=0.\nonumber$$

Notice that $y$ and its derivatives appear in a relatively simple form. They are multiplied by functions of $x$, but are not raised to any powers themselves, nor are they multiplied together. As discussed in previously, first-order equations with similar characteristics are said to be linear. The same is true of second-order equations. Also note that all the terms in this differential equation involve either $y$ or one of its derivatives. There are no terms involving only functions of $x$. Equations like this, in which every term contains $y$ or one of its derivatives, are called homogeneous.

Not all differential equations are homogeneous. Consider the differential equation

$$xy''+2x^2y'+5x^3y=x^2.\nonumber$$

The $x^2$ term on the right side of the equal sign does not contain $y$ or any of its derivatives. Therefore, this differential equation is nonhomogeneous.

Definition: Homogeneous and Nonhomogeneous Linear Equations

A second-order differential equation is linear if it can be written in the form

$$a_{2}(x)y''+a){1}(x)y'+a_{0}(x)y=r(x), \label{17.1}$$

where $a_{2}(x), a_{1}(x), a_{0}(x),$ and $r(x)$ are real-valued functions and $a_{2}(x)$ is not identically zero. If $r(x) \equiv 0$—in other words, if $r(x)=0$ for every value of $x$—the equation is said to be a homogeneous linear equation. If $r(x) \neq 0$ for some value of $x,$ the equation is said to be a nonhomogeneous linear equation.

In linear differential equations, $y$ and its derivatives can be raised only to the first power and they may not be multiplied by one another. Terms involving $y^2$ or $\sqrt{y'}$ make the equation nonlinear. Functions of $y$ and its derivatives, such as $\sin y$ or $e^{y'}$, are similarly prohibited in linear differential equations.

Note that equations may not always be given in standard form (the form shown in the definition). It can be helpful to rewrite them in that form to decide whether they are linear, or whether a linear equation is homogeneous.

Example $\PageIndex{1}$: Classifying Second-Order Equations

Classify each of the following equations as linear or nonlinear. If the equation is linear, determine further whether it is homogeneous or nonhomogeneous.

1. $y''+3x^4y'+x^2y^2=x^3$
2. $(\sin x)y''+(\cos x)y'+3y=0$
3. $4t^2x''+3txx'+4x=0$
4. $5y''+y=4x^5$
5. $( \cos x)y''- \sin y'+( \sin x)y- \cos x=0$
6. $8ty''-6t^2y'+4ty-3t^2=0$
7. $\sin(x^2)y''-( \cos x)y'+x^2y=y'-3$
8. $y''+5xy'-3y= \cos y$

Solution

1. This equation is nonlinear because of the $y^2$ term.
2. This equation is linear. There is no term involving a power or function of $y,$ and the coefficients are all functions of $x$.The equation is already written in standard form, and $r(x)$ is identically zero, so the equation is homogeneous.
3. This equation is nonlinear. Note that, in this case, $x$ is the dependent variable and $t$is the independent variable. The second term involves the product of $x$ and $x'$, so the equation is nonlinear.
4. This equation is linear. Since $r(x)=4x^5,$ the equation is nonhomogeneous.
5. This equation is nonlinear, because of the $\sin y'$ term.
6. This equation is linear. Rewriting it in standard form gives

   $$8t^2y''-6t^2y'+4ty=3t^2. \nonumber$$

   With the equation in standard form, we can see that $r(t)=3t^2,$so the equation is nonhomogeneous.
7. This equation looks like it’s linear, but we should rewrite it in standard form to be sure. We get

   $$\sin(x^2)y''-(\cos x+1)y'+x^2y=-3. \nonumber$$

   This equation is, indeed, linear. With $r(x)=-3,$ it is nonhomogeneous.
8. This equation is nonlinear because of the $\cos y$ term.

Exercise $\PageIndex{1}$

Classify each of the following equations as linear or nonlinear. If the equation is linear, determine further whether it is homogeneous or nonhomogeneous.

1. $(y'')2-y'+8x^3y=0$
2. $(\sin t)y''+ \cos t-3ty'=0$

Hint

Write the equation in standard form (Equation $\ref{17.1}$) if necessary. Check for powers or functions of $y$ and its derivatives.

Answer a

Nonlinear Linear

Answer b

nonhomogeneous

Later in this section, we will see some techniques for solving specific types of differential equations. Before we get to that, however, let’s get a feel for how solutions to linear differential equations behave. In many cases, solving differential equations depends on making educated guesses about what the solution might look like. Knowing how various types of solutions behave will be helpful.

Example $\PageIndex{2}$: Verifying a Solution

Consider the linear, homogeneous differential equation

$$x^2y''-xy′-3y=0. \nonumber$$

Looking at this equation, notice that the coefficient functions are polynomials, with higher powers of $x$ associated with higher-order derivatives of $y$. Show that $y=x^3$ is a solution to this differential equation.

Solution

Let $y=x^3.$ Then $y'=3x^2$ and $y''=6x.$ Substituting into the differential equation, we see that

$$\begin{align*} x^2y''-xy'-3y &=x^2(6x)-x(3x^2)-3(x^3) \\[4pt] &=6x^3-3x^3-3x^3 \\[4pt] &=0. \end{align*}$$

Exercise $\PageIndex{2}$

Show that $y=2x^2$ is a solution to the differential equation

$$\dfrac{1}{2}x^2y''-xy'+y=0. \label{ex2}$$

Hint

Calculate the derivatives and substitute them into the differential equation.

Answer

This requires calculating $y'$ and $y''$.

$$y' = \dfrac{dy}{dx} = 4x \nonumber$$

and

$$y'' = \dfrac{dy'}{dx} = 4 \nonumber$$

Inserting these derivatives along with $y=2x^2$ into Equation $\ref{ex2}$.

$$\begin{align*} \dfrac{1}{2}x^2y''-xy'+y &\overset{?}{=} 0 \\[4pt] \dfrac{1}{2}x^2(4) - x (4x) + 2x^2 &\overset{?}{=} 0 \\[4pt] 2x^2 - 4x^2 + 2x^2 &\overset{\checkmark}{=} 0 \end{align*} \nonumber$$

Yes, this is a solution to the differential equation in Equation $\ref{ex2}$.

Although simply finding any solution to a differential equation is important, mathematicians and engineers often want to go beyond finding one solution to a differential equation to finding all solutions to a differential equation. In other words, we want to find a general solution. Just as with first-order differential equations, a general solution (or family of solutions) gives the entire set of solutions to a differential equation. An important difference between first-order and second-order equations is that, with second-order equations, we typically need to find two different solutions to the equation to find the general solution. If we find two solutions, then any linear combination of these solutions is also a solution. We state this fact as the following theorem.

Theorem: SUPERPOSITION PRINCIPLE

If $y_1(x)$ and $y_2(x)$ are solutions to a linear homogeneous differential equation, then the function

$$y(x)=c_1y_1(x)+c_2y_2(x), \label{super}$$

where $c_1$ and $c_2$ are constants, is also a solution.

The proof of this superposition principle theorem is left as an exercise.

Example $\PageIndex{3}$: Verifying the Superposition Principle

Consider the differential equation

$$y''-4y'-5y=0.\nonumber$$

Given that $e^{-x}$ and $e^{5x}$ are solutions to this differential equation, show that $4e^{-x}+e^{5x}$ is a solution.

Solution

Although this can be done through a simple application of the Superposition principle (Equation $\ref{super}$), but we can also confirm it is a solution via an approach like in Example $\PageIndex{2}$. We have

$$\begin{align*} y(x) &=4e^{-x}+e^{5x} \\[4pt] y'(x) &= -4e^{-x} + 5e^{5x} \\[4pt] y''(x) &=4e^{-x}+25e^{5x}. \end{align*}$$

Then

$$\begin{align*} y''-4y'-5y &\overset{?}{=} (4e^{-x}+25e^{5x})-4(-4e^{-x}+5e^{5x})-5(4e^{-x}+e^{5x}) \\[4pt] &\overset{?}{=} 4e^{-x}+25e^{5x}+16e^{-x}-20e^{5x}-20e^{-x}-5e^{5x} \\[4pt] &\overset{\checkmark}{=}0. \end{align*} \nonumber$$

Thus, $y(x)=4e^{-x}+e^{5x}$ is a solution.

Exercise $\PageIndex{3}$

Consider the differential equation

$$y''+5y'+6y=0. \nonumber$$

Given that $e^{-2x}$ and $e^{-3x}$ are solutions to this differential equation, show that $3e^{-2x}+6e^{-3x}$ is a solution.

Hint

Differentiate the function and substitute into the differential equation.

Answer

Although this can be a simple application of the Superposition principle (Equation $\ref{super}$), we can also set through it like in Example $\PageIndex{2}$. We have

$$\begin{align*} y(x) &=3e^{-2x}+6e^{-3x} \\[4pt] y'(x) &= -6 e^{-2x} - 18e^{-3x} \\[4pt] y''(x) &= 12e^{-2x} + 54e^{3x}. \end{align*}$$

Then

$$\begin{align*} y''+5y'+6y &= (12e^{-2x} + 54e^{3x}) + 5( -6 e^{-2x} - 18e^{-3x} ) + 6( 3e^{-2x} + 6e^{3x}) \\[4pt] &\overset{?}{=} \cancel{12e^{-2x}} + \bcancel{54e^{3x}} - \cancel{30e^{-2x}} - \bcancel{90e^{3x}} + \cancel{18e^{-2x}} + \bcancel{36e^{3x}} \\[4pt] &\overset{\checkmark}{=}0. \end{align*} \nonumber$$

Thus, $3e^{-2x}+6e^{-3x}$ is a solution to the differential equation

Unfortunately, to find the general solution to a second-order differential equation, it is not enough to find any two solutions and then combine them. Consider the differential equation

$$x''+7x'+12x=0.\nonumber$$

Both $e^{-3t}$ and $2e^{-3t}$ are solutions (you can check this). However,

$$x(t)=c_1e^{-3t}+c_2(2e^{-3t})\nonumber$$

is not the general solution. This expression does not account for all solutions to the differential equation. In particular, it fails to account for the function $e^{-4t},$ which is also a solution to the differential equation. It turns out that to find the general solution to a second-order differential equation, we must find two linearly independent solutions. We define that terminology here.

Definition: Linearly Dependent functions

A set of functions $f_1(x),\, f_2(x), \ldots ,f_n(x)$ is said to be linearly dependent if there are constants $c_1,\, c_2, \ldots c_n,$, not all zero, such that

$$c_1f_1(x)+c_2f_2(x)+ \cdots +c_nf_n(x)=0 \nonumber$$

for all $x$ over the interval of interest. A set of functions that is not linearly dependent is said to be linearly independent.

In this chapter, we usually test sets of only two functions for linear independence, which allows us to simplify this definition. From a practical perspective, we see that two functions are linearly dependent if either one of them is identically zero or if they are constant multiples of each other.

First we show that if the functions meet the conditions given previously, then they are linearly dependent. If one of the functions is identically zero—say, $f_2(x) \equiv 0$—then choose $c_1=0$ and $c_2=1,$ and the condition for linear dependence is satisfied. If, on the other hand, neither $f_1(x)$ nor $f_2(x)$ is identically zero, but $f_1(x)=Cf_2(x)$ for some constant $C,$ then choose $c_1=C$ and $c_2=-1,$ and again, the condition is satisfied.

Next, we show that if two functions are linearly dependent, then either one is identically zero or they are constant multiples of one another. Assume $f_1(x)$ and $f_2(x)$ are linearly independent. Then, there are constants, $c_1$ and $c_2,$ not both zero, such that

$$c_1f_1(x)+c_2f_2(x)=0 \nonumber$$

for all $x$ over the interval of interest. Then,

$$c_1f_1(x)=-c_2f_2(x). \nonumber$$

Now, since we stated that $c_1$ and $c_2$ can’t both be zero, assume $c_2 \neq 0.$ Then, there are two cases: either $c_1=0$ or $c_1\neq 0.$ If $c_1=0,$ then

$$\begin{align*} 0 &=-c_2f_2(x) \\[4pt] 0 &=f_2(x), \end{align*}$$

so one of the functions is identically zero. Now suppose $c_1 \neq 0.$ Then,

$$f_1(x)=\left(- \dfrac{c_2}{c_1}\right)f_2(x) \nonumber$$

and we see that the functions are constant multiples of one another.

Theorem: Linear Dependence of Two Functions

Two functions, $f_1(x)$ and $f_2(x),$ are said to be linearly dependent if either one of them is identically zero or if $f_1(x)=Cf_2(x)$ for some constant $C$ and for all $x$ over the interval of interest. Functions that are not linearly dependent are said to be linearly independent.

Example $\PageIndex{4}$: Testing for Linear Dependence

Determine whether the following pairs of functions are linearly dependent or linearly independent.

1. $f_1(x)=x^2$ and $f_2(x)=5x^2$
2. $f_1(x)= \sin x$ and $f_2(x)= \cos x$
3. $f_1(x)=e^{3x}$ and $f_2(x)=e^{-3x}$
4. $f_1(x)=3x$ and $f_2(x)=3x+1$

Solution

1. $f_2(x)=5f_1(x),$ so the functions are linearly dependent.
2. There is no constant $C$ such that $f_1(x)=Cf_2(x),$ so the functions are linearly independent.
3. There is no constant $C$ such that $f_1(x)=Cf_2(x),$ so the functions are linearly independent. Don’t get confused by the fact that the exponents are constant multiples of each other. With two exponential functions, unless the exponents are equal, the functions are linearly independent.
4. There is no constant $C$ such that $f_1(x)=Cf_2(x),$ so the functions are linearly independent.

Exercise $\PageIndex{4}$

Determine whether the following pairs of functions are linearly dependent or linearly independent: $f_1(x)=e^{x}$ and $f_2(x)=3e^{3x}.$

Hint

Are the functions constant multiples of one another?

Answer

Linearly independent

If we are able to find two linearly independent solutions to a second-order differential equation, then we can combine them to find the general solution. This result is formally stated in the following theorem.

Theorem: General Solution to a Homogeneous Equation

If $y_1(x)$ and $y_2(x)$ are linearly independent solutions to a second-order, linear, homogeneous differential equation, then the general solution is given by

$$y(x)=c_1y_1(x)+c_2y_2(x), \nonumber$$

where $c_1$ and $c_2$ are constants.

When we say a family of functions is the general solution to a differential equation, we mean that

1. every expression of that form is a solution and
2. every solution to the differential equation can be written in that form, which makes this theorem extremely powerful.

If we can find two linearly independent solutions to a second order differential equation, we have, effectively, found all solutions to the second order differential equation—quite a remarkable statement. The proof of this theorem is beyond the scope of this text.

Example $\PageIndex{5}$: Writing the General Solution

If $y_1(t)=e^{3t}$ and $y_2(t)=e^{-3t}$ are solutions to $y''-9y=0,$ what is the general solution?

Solution

Note that $y_1$ and $y_2$ are not constant multiples of one another, so they are linearly independent. Then, the general solution to the differential equation is

$y(t)=c_1e^{3t}+c_2e^{-3t}.$

Exercise $\PageIndex{5}$

If $y_1(x)=e^{3x}$ and $y_2(x)=xe^{3x}$ are solutions to $y''-6y'+9y=0,$ what is the general solution?

Hint

Check for linear independence first.

Answer

$y(x)=c_1e^{3x}+c_2xe^{3x}$

Second-Order Equations with Constant Coefficients

Now that we have a better feel for linear differential equations, we are going to concentrate on solving second-order equations of the form

$$ay''+by'+cy=0, \tag{17.2}$$

where $a, b,$ and $c$ are constants.

Since all the coefficients are constants, the solutions are probably going to be functions with derivatives that are constant multiples of themselves. We need all the terms to cancel out, and if taking a derivative introduces a term that is not a constant multiple of the original function, it is difficult to see how that term cancels out. Exponential functions have derivatives that are constant multiples of the original function, so let’s see what happens when we try a solution of the form $y(x)=e^{ \lambda x}$, where $\lambda$ (the lowercase Greek letter lambda) is some constant.

If $y(x)=e^{ \lambda x}$, then $y'(x)= \lambda e^{ \lambda x}$ and $y''= \lambda^2 e^{ \lambda x}.$ Substituting these expressions into Equation $\ref{17.1}$, we get

$$\begin{align*} ay''+by'+cy &= a(\lambda^2e^{\lambda x})+b(\lambda e^{\lambda x})+ce^{\lambda x} \\[4pt] &=e^{\lambda x}(a \lambda^2+b \lambda +c). \end{align*}$$

Since $e^{\lambda x}$ is never zero, this expression can be equal to zero for all $x$ only if

$$a\lambda^2+b\lambda +c=0. \nonumber$$

We call this the characteristic equation of the differential equation.

Definition: characteristic equation

The characteristic equation of the second order differential equation $ay''+by'+cy=0$ is

$$a\lambda^2+b\lambda +c=0. \nonumber$$

The characteristic equation is very important in finding solutions to differential equations of this form. We can solve the characteristic equation either by factoring or by using the quadratic formula

$$\lambda = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}. \nonumber$$

This gives three cases. The characteristic equation has

1. distinct real roots;
2. a single, repeated real root; or
3. complex conjugate roots.

We consider each of these cases separately.

Case 1: Distinct Real Roots

If the characteristic equation has distinct real roots $\lambda_1$ and $\lambda_2$, then $e^{\lambda_1x}$ and $e^{\lambda_2x}$ are linearly independent solutions to Example $\ref{17.1}$, and the general solution is given by

$$y(x)=c_1e^{\lambda_1x}+c_2e^{\lambda_2x}, \nonumber$$

where $c_1$ and $c_2$ are constants.

For example, the differential equation $y''+9y'+14y=0$ has the associated characteristic equation $\lambda^2+9\lambda+14=0.$ This factors into $(\lambda +2)(\lambda +7)=0,$ which has roots $\lambda_1=-2$ and $\lambda_2=-7.$ Therefore, the general solution to this differential equation is

$$y(x)=c_1e^{-2x}+c_2e^{-7x}. \nonumber$$

Case 2: Single Repeated Real Root

Things are a little more complicated if the characteristic equation has a repeated real root, $\lambda$. In this case, we know $e^{\lambda x}$ is a solution to Equation $\ref{17.1}$, but it is only one solution and we need two linearly independent solutions to determine the general solution. We might be tempted to try a function of the form $ke^{\lambda x},$ where $k$ is some constant, but it would not be linearly independent of $e^{\lambda x}.$ Therefore, let’s try $xe^{\lambda x}$ as the second solution. First, note that by the quadratic formula,

$$\lambda = \frac{-b \pm \sqrt{b^2-4ac}}{2a}. \nonumber$$

But, $\lambda$ is a repeated root, so the discriminate ($b^2-4ac$) is zero and $\lambda = \frac{-b}{2a}$. Thus, if $y=xe^{\lambda x}$, we have

$$\begin{align*} y' =e^{\lambda x}+ \lambda xe^{\lambda x} \\[4pt] y'' =2\lambda e^{\lambda x}+\lambda^2xe^{\lambda x}. \end{align*}$$

Substituting both expressions into Equation $\ref{17.1}$, we see that

$$\begin{align*} ay''+by′+cy &=a(2λe^{λx}+λ^2xe^{λx})+b(e^{λx}+λxe^{λx})+cxe^{λx} \\[4pt] &=xe^{λx}(aλ^2+bλ+c)+e^{λx}(2aλ+b) \\[4pt] &=xe^{λx}(0)+e^{λx}(2a(−b2a)+b)\\[4pt] &=0+e^{λx}(0) \\[4pt] &\overset{\checkmark}{=}0. \end{align*}$$

This shows that $xe^{\lambda x}$ is a solution to Equation $\ref{17.1}$. Since $e^{\lambda x}$ and $xe^{\lambda x}$ are linearly independent, when the characteristic equation has a repeated root $\lambda$, the general solution to Equation $\ref{17.1}$ is given by

$$y(x)=c_1e^{\lambda x}+c_2xe^{\lambda x}, \nonumber$$

where $c_1$ and $c_2$ are constants.

For example, the differential equation $y''+12y'+36y=0$ has the associated characteristic equation

$$\lambda^2+12 \lambda +36=0.\nonumber$$

This factors into $(\lambda +6)^2=0,$ which has a repeated root $\lambda =-6$. Therefore, the general solution to this differential equation is

$$y(x)=c_1e^{-6x}+c_2xe^{-6x}.\nonumber$$

Case 3: Complex Conjugate Roots

The third case we must consider is when $b^2-4ac <0.$ In this case, when we apply the quadratic formula, we are taking the square root of a negative number. We must use the imaginary number $i= \sqrt{-1}$ to find the roots, which take the form $\lambda_1= \alpha + \beta i$ and $\lambda _2=\alpha -\beta i.$ The complex number $\alpha +\beta i$ is called the conjugate of $\alpha -\beta i$. Thus, we see that when the discriminate $b^2-4ac$ is negative, the roots of our characteristic equation are always complex conjugates.

This creates a little bit of a problem for us. If we follow the same process we used for distinct real roots—using the roots of the characteristic equation as the coefficients in the exponents of exponential functions—we get the functions $e^{(\alpha + \beta i)x}$ and $e^{(\alpha - \beta i)x}$ as our solutions. However, there are problems with this approach. First, these functions take on complex (imaginary) values, and a complete discussion of such functions is beyond the scope of this text. Second, even if we were comfortable with complex-value functions, in this course we do not address the idea of a derivative for such functions. So, if possible, we’d like to find two linearly independent real-value solutions to the differential equation. For purposes of this development, we are going to manipulate and differentiate the functions $e^{(\alpha + \beta i)x}$ and $e^{(\alpha - \beta i)x}$ as if they were real-value functions. For these particular functions, this approach is valid mathematically, but be aware that there are other instances when complex-value functions do not follow the same rules as real-value functions. Those of you interested in a more in-depth discussion of complex-value functions should consult a complex analysis text.

Based on the roots $\alpha \pm \beta i$ of the characteristic equation, the functions $e^{(\alpha + \beta i)x}$ and $e^{(\alpha - \beta i)x}$ are linearly independent solutions to the differential equation and the general solution is given by

$$y(x)=c_1e^{(\alpha +\beta i)x}+c_2e^{(\alpha - \beta i)x}. \nonumber$$

Using some smart choices for $c_1$ and $c_2$, and a little bit of algebraic manipulation, we can find two linearly independent, real-value solutions to Equation $\ref{17.1}$ and express our general solution in those terms.

We encountered exponential functions with complex exponents earlier. One of the key tools we used to express these exponential functions in terms of sines and cosines was Euler’s formula, which tells us that

$$\underbrace{e^{i \theta }= \cos \theta+ i \sin \theta}_{\text{Euler’s formula}} \label{Euler}$$

for all real numbers $\theta$.

Going back to the general solution, we have

$$\begin{align*} y(x) &=c_1e^{( \alpha+ \beta i)x}+c_2e^{(\alpha - \beta i)x} \\[4pt] &=c_1e^{\alpha x}e^{\beta ix}+c_2e^{\alpha x}e^{- \beta ix} \\[4pt] &=e^{\alpha x}(c_1e^{\beta ix}+c_2e^{-\beta ix}).\end{align*}$$

Applying Euler’s formula (Equation $\ref{Euler}$) together with the identities $\cos(-x)=\cos x$ and $\sin(-x)=- \sin x,$ we get

$$\begin{align} y(x) &=e^{\alpha x}[c_1(\cos \beta x+i \sin \beta x)+c_2(\cos(- \beta x)+i \sin(- \beta x))] \nonumber \\[4pt] &=e^{\alpha x}[(c_1+c_2)\cos \beta x+(c_1-c_2)i \sin \beta x]. \label{E1}\end{align}$$

Now, if we choose $c_1=c_2= \frac{1}{2},$ the second term is zero and we get

$$y(x)=e^{\alpha x} \cos \beta x \nonumber$$

as a real-value solution to Equation $\ref{17.1}$. Similarly, if we choose $c_1=−\frac{i}{2}$ and $c_2=\frac{i}{2}$, the first term of Equation $\ref{E1}$ is zero and we get

$$y(x)=e^{\alpha x} \sin \beta x \nonumber$$

as a second, linearly independent, real-value solution to Equation $\ref{17.1}$.

Based on this, we see that if the characteristic equation has complex conjugate roots $\alpha \pm \beta i,$ then the general solution to Equation $\ref{17.1}$ is given by

$$\begin{align*} y(x) &=c_1e^{\alpha x} \cos \beta x+c_2e^{\alpha x} \sin \beta x \\[4pt] &=e^{\alpha x}(c_1 \cos \beta x+c_2 \sin \beta x),\end{align*}$$

where $c_1$ and $c_2$ are constants.

For example, the differential equation $y''-2y'+5y=0$ has the associated characteristic equation $\lambda ^2-2 \lambda +5=0.$ By the quadratic formula, the roots of the characteristic equation are $1\pm 2i.$ Therefore, the general solution to this differential equation is

$$y(x)=e^{x}(c_1 \cos 2x+c_2 \sin 2x).\nonumber$$

Summary of Results

We can solve second-order, linear, homogeneous differential equations with constant coefficients by finding the roots of the associated characteristic equation. The form of the general solution varies, depending on whether the characteristic equation has distinct, real roots; a single, repeated real root; or complex conjugate roots. The three cases are summarized in Table $\PageIndex{1}$.

Table $\PageIndex{1}$: Summary of Characteristic Equation Cases

Characteristic Equation Roots	General Solution to the Differential Equation
Distinct real roots, $\lambda_1$ and $\lambda_2$	$y(x)=c_1e^{\lambda_1x}+c_2e^{\lambda_2x}$
A repeated real root, $\lambda$	$y(x)=c_1e^{\lambda x}+c_2xe^{\lambda x}$
Complex conjugate roots $\alpha \pm \beta i$	$y(x)=e^{\alpha x}(c_1 \cos \beta x+c_2 \sin \beta x)$

PROBLEM-SOLVING STRATEGY: USING THE CHARACTERISTIC EQUATION TO SOLVE SECOND-ORDER DIFFERENTIAL EQUATIONS WITH CONSTANT COEFFICIENTS

1. Write the differential equation in the form $a''+by'+cy=0.$
2. Find the corresponding characteristic equation $a\lambda^2+b\lambda +c=0.$
3. Either factor the characteristic equation or use the quadratic formula to find the roots.
4. Determine the form of the general solution based on whether the characteristic equation has distinct, real roots; a single, repeated real root; or complex conjugate roots.

Example $\PageIndex{6}$: Solving Second-Order Equations with Constant Coefficients

Find the general solution to the following differential equations. Give your answers as functions of $x$.

1. $y''+3y'-4y=0$
2. $y''+6y'+13y=0$
3. $y''+2y'+y=0$
4. $y''-5y'=0$
5. $y''-16y=0$
6. $y''+16y=0$

Solution

Note that all these equations are already given in standard form (step 1).

1. The characteristic equation is $\lambda^2+3\lambda -4=0$ (step 2). This factors into $(\lambda +4)(\lambda -1)=0$, so the roots of the characteristic equation are $\lambda_1=-4$ and $\lambda_2=1$ (step 3). Then the general solution to the differential equation is

   $$y(x)=c_1e^{-4x}+c_2e^{x}. \tag{step 1}$$

2. The characteristic equation is $\lambda^2+6\lambda+13=0$ (step 2). Applying the quadratic formula, we see this equation has complex conjugate roots $-3\pm 2i$ (step 3). Then the general solution to the differential equation is

   $$y(t)=e^{-3t}(c_1 \cos 2t+c_2 \sin 2t). \tag{step 2}$$

3. The characteristic equation is $\lambda^2+2\lambda+1=0$ (step 2). This factors into $(\lambda+1)2=0,$ so the characteristic equation has a repeated real root $\lambda =-1$ (step 3). Then the general solution to the differential equation is

   $$y(t)=c_1e^{-t}+c_2te^{-t}. \tag{step 3}$$

4. The characteristic equation is $\lambda^2-5\lambda$ (step 2). This factors into $\lambda(\lambda -5)=0,$ so the roots of the characteristic equation are $\lambda_1=0$ and $\lambda_2=5$ (step 3). Note that $e^{0x}=e^{0}=1$, so our first solution is just a constant. Then the general solution to the differential equation is

   $$y(x)=c_1+c_2e^{5x}. \tag{step 4}$$

5. The characteristic equation is $\lambda^2-16=0$ (step 2). This factors into $(\lambda+4)(\lambda -4)=0,$ so the roots of the characteristic equation are $\lambda_1=4$ and $\lambda_2=-4$ (step 3). Then the general solution to the differential equation is

   $$y(x)=c_1e^{4x}+c_2e^{-4x}. \tag{step 5}$$

6. The characteristic equation is $\lambda^2+16=0$ (step 2). This has complex conjugate roots $\pm 4i$ (step 3). Note that $e^{0x}=e^0=1$, so the exponential term in our solution is just a constant. Then the general solution to the differential equation is

   $$y(t)=c_1 \cos 4t+c_2 \sin 4t. \tag{step 6}$$

Exercise $\PageIndex{6}$

Find the general solution to the following differential equations:

1. $y''-2y'+10y=0$
2. $y''+14y'+49y=0$

Hint

Find the roots of the characteristic equation.

Answer a

$y(x)=e^x(c_1 \cos 3x+c_2 \sin 3x)$

Answer b

$y(x)=c_1e^{-7x}+c_2xe^{-7x}$

Initial-Value Problems and Boundary-Value Problems

So far, we have been finding general solutions to differential equations. However, differential equations are often used to describe physical systems, and the person studying that physical system usually knows something about the state of that system at one or more points in time. For example, if a constant-coefficient differential equation is representing how far a motorcycle shock absorber is compressed, we might know that the rider is sitting still on his motorcycle at the start of a race, time $t=t_0.$ This means the system is at equilibrium, so $y(t_0)=0,$ and the compression of the shock absorber is not changing, so $y'(t_0)=0.$ With these two initial conditions and the general solution to the differential equation, we can find the specific solution to the differential equation that satisfies both initial conditions. This process is known as solving an initial-value problem. (Recall that we discussed initial-value problems in Introduction to Differential Equations.) Note that second-order equations have two arbitrary constants in the general solution, and therefore we require two initial conditions to find the solution to the initial-value problem.

Sometimes we know the condition of the system at two different times. For example, we might know $y(t_0)=y_0$ and $y(t_1)=y_1.$These conditions are called boundary conditions, and finding the solution to the differential equation that satisfies the boundary conditions is called solving a boundary-value problem.

Mathematicians, scientists, and engineers are interested in understanding the conditions under which an initial-value problem or a boundary-value problem has a unique solution. Although a complete treatment of this topic is beyond the scope of this text, it is useful to know that, within the context of constant-coefficient, second-order equations, initial-value problems are guaranteed to have a unique solution as long as two initial conditions are provided. Boundary-value problems, however, are not as well behaved. Even when two boundary conditions are known, we may encounter boundary-value problems with unique solutions, many solutions, or no solution at all.

Example $\PageIndex{7}$: Solving an Initial-Value Problem

Solve the following initial-value problem: $y''+3y'-4y=0, \, y(0)=1,\, y'(0)=-9.$

Solution

We already solved this differential equation in Example 17.6a. and found the general solution to be

$$y(x)=c_1e^{-4x}+c_2e^{x}. \nonumber$$

Then

$$y'(x)=-4c_1e^{-4x}+c_2e^{x}. \nonumber$$

When $x=0,$ we have $y(0)=c_1+c_2$ and $y'(0)=-4c_1+c_2.$ Applying the initial conditions, we have

$$\begin{align*} c_1+c_2 &=1 \\[4pt] -4c_1+c_2 &=-9.\end{align*}$$

Then $c_1=1-c_2.$ Substituting this expression into the second equation, we see that

$$\begin{align*} -4(1-c_2)+c_2 &= -9 \\[4pt] -4+4c_2+c_2 &=-9 \\[4pt] 5c_2 &=-5 \\[4pt] c_2 &=-1. \end{align*}$$

So, $c_1=2$ and the solution to the initial-value problem is

$$y(x)=2e^{-4x}-e^{x}. \nonumber$$

Exercise $\PageIndex{7}$

Solve the initial-value problem $y''-3y'-10y=0, \quad y(0)=0, \; y'(0)=7.$

Hint

Use the initial conditions to determine values for $c_1$ and $c_2$.

Answer

$$y(x)=-e^{-2x}+e^{5x} \nonumber$$

Example $\PageIndex{8}$: Solving an Initial-Value Problem and Graphing the Solution

Solve the following initial-value problem and graph the solution:

$$y''+6y'+13y=0, \quad y(0)=0, \; y'(0)=2\nonumber$$

Solution

We already solved this differential equation in Example $\PageIndex{6b}$. and found the general solution to be

$$y(x)=e^{-3x}(c_1 \cos 2x+c_2 \sin 2x).\nonumber$$

Then

$$y'(x)=e^{-3x}(-2c_1 \sin 2x+2c_2 \cos 2x)-3e^{-3x}(c_1 \cos 2x+c_2 \sin 2x). \nonumber$$

When $x=0,$ we have $y(0)=c_1$ and $y'(0)=2c_2-3c_1$. Applying the initial conditions, we obtain

$$\begin{align*} c_1 &=0 \\[4pt] -3c_1+2c_2 &=2. \end{align*}$$

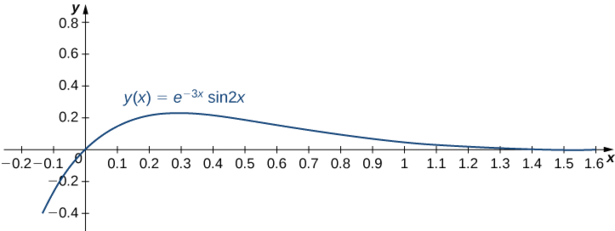
Therefore, $c_1=0, \, c_2=1,$ and the solution to the initial value problem is shown in the following graph.

$$y=e^{-3x} \sin 2x.\nonumber$$

Exercise $\PageIndex{8}$

Solve the following initial-value problem and graph the solution: $y''-2y'+10y=0, \quad y(0)=2, \; y'(0)=-1$

Hint

Use the initial conditions to determine values for $c_1$ and $c_2.$

Answer

$$y(x)=e^{x}(2 \cos 3x - \sin 3x) \nonumber$$

Example $\PageIndex{9}$: Initial-Value Problem Representing a Spring-Mass System

The following initial-value problem models the position of an object with mass attached to a spring. Spring-mass systems are examined in detail in Applications. The solution to the differential equation gives the position of the mass with respect to a neutral (equilibrium) position (in meters) at any given time. (Note that for spring-mass systems of this type, it is customary to define the downward direction as positive.)

$$y''+2y'+y=0, \quad y(0)=1, \; y'(0)=0 \nonumber$$

Solve the initial-value problem and graph the solution. What is the position of the mass at time $t=2$ sec? How fast is the mass moving at time $t=1$ sec? In what direction?

Solution

In Example Example $\PageIndex{6c}$. we found the general solution to this differential equation to be

$$y(t)=c_1e^{-t}+c_2te^{-t}. \nonumber$$

Then

$$y'(t)=-c_1e^{-t}+c_2(-te^{-t}+e^{-t}). \nonumber$$

When $t=0,$ we have $y(0)=c_1$ and $y'(0)=c_1+c_2.$ Applying the initial conditions, we obtain

$$c_1=1 \\ -c_1+c_2=0. \nonumber$$

Thus, $c_1=1, c_2=1,$ and the solution to the initial value problem is

$$y(t)=e^{-t}+te^{-t}. \nonumber$$

This solution is represented in the following graph. At time $t=2,$ the mass is at position $y(2)=e^{-2}+2e^{-2}=3e^{-2} \approx 0.406$ m below equilibrium.

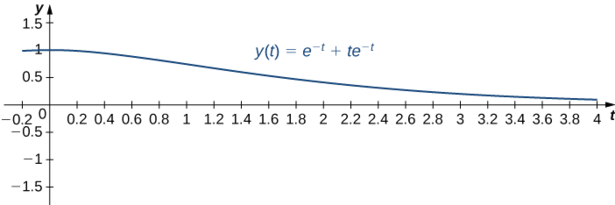
To calculate the velocity at time $t=1,$ we need to find the derivative. We have $y(t)=e^{-t}+te^{-t},$ so

$$y'(t)=-e^{-t}+e^{-t}-te^{-t}= -te^{-t}. \nonumber$$

Then $y'(1)=-e^{-1} \approx -0.3679$. At time $t=1,$ the mass is moving upward at $0.3679$ m/sec.

Exercise $\PageIndex{9}$

Suppose the following initial-value problem models the position (in feet) of a mass in a spring-mass system at any given time. Solve the initial-value problem and graph the solution. What is the position of the mass at time $t=0.3$ sec? How fast is it moving at time $t=0.1$ sec? In what direction?

$$y''+14y'+49y=0, \quad y(0)=0, \; y'(0)=1 \nonumber$$

Hint

Use the initial conditions to determine values for $c_1$ and $c_2$.

Answer

$$y(t)=te^{-7t}\nonumber$$

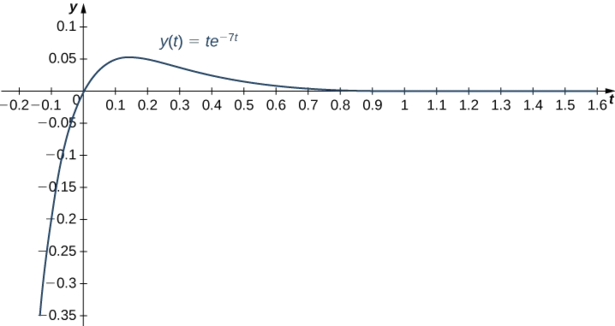
At time $t=0.3, \; y(0.3)=0.3e^{(-7^{\ast} 0.3)}=0.3e^{-2.1} \approx 0.0367.$ The mass is $0.0367$ft below equilibrium. At time $t=0.1, \; y'(0.1)=0.3e^{-0.7} \approx 0.1490.$ The mass is moving downward at a speed of $0.1490$ ft/sec.

Example $\PageIndex{10}$: Solving a Boundary-Value Problem

In Example 17.6f. we solved the differential equation $y''+16y=0$ and found the general solution to be $y(t)=c_1 \cos 4t+c_2 \sin 4t.$ If possible, solve the boundary-value problem if the boundary conditions are the following:

1. $y(0)=0, y( \frac{\pi}{4})=0$
2. $y(0)=1,y(0)=1, y(\frac{\pi}{8})=0$
3. $y(\frac{\pi}{8})=0, y(\frac{3 \pi}{8})=2$

Solution

We have

$$y(x)=c_1 \cos 4t+c_2 \sin 4t. \nonumber$$

1. Applying the first boundary condition given here, we get $y(0)=c_1=0.$ So the solution is of the form $y(t)=c_2 \sin 4t.$ When we apply the second boundary condition, though, we get $y(\frac{\pi}{4})=c_2 \sin(4(\frac{\pi}{4}))=c_2 \sin \pi =0$ for all values of $c_2$. The boundary conditions are not sufficient to determine a value for $c_2,$ so this boundary-value problem has infinitely many solutions. Thus, $y(t)=c_2 \sin 4t$ is a solution for any value of $c_2$.
2. Applying the first boundary condition given here, we get $y(0)=c_1=1.$ Applying the second boundary condition gives $y(\frac{\pi}{8})=c_2=0,$ so $c_2=0.$ In this case, we have a unique solution: $y(t)= \cos 4t$.
3. Applying the first boundary condition given here, we get $y(\frac{\pi}{8})=c_2=0.$ However, applying the second boundary condition gives $y(\frac{3 \pi}{8})=-c_2=2,$ so $c_2=-2.$ We cannot have $c_2=0=-2,$ so this boundary value problem has no solution.

Key Concepts

• Second-order differential equations can be classified as linear or nonlinear, homogeneous or nonhomogeneous.
• To find a general solution for a homogeneous second-order differential equation, we must find two linearly independent solutions. If $y_1(x)$ and $y_2(x)$ are linearly independent solutions to a second-order, linear, homogeneous differential equation, then the general solution is given by

  $$y(x)=c_1y_1(x)+c_2y_2(x).\nonumber$$

• To solve homogeneous second-order differential equations with constant coefficients, find the roots of the characteristic equation. The form of the general solution varies depending on whether the characteristic equation has distinct, real roots; a single, repeated real root; or complex conjugate roots.
• Initial conditions or boundary conditions can then be used to find the specific solution to a differential equation that satisfies those conditions, except when there is no solution or infinitely many solutions.

Key Equations

• Linear second-order differential equation $$a_2(x)y''+a_1(x)y'+a_0(x)y=r(x) \nonumber$$
• Second-order equation with constant coefficients $$ay''+by'+cy=0 \nonumber$$

Glossary

boundary conditions

the conditions that give the state of a system at different times, such as the position of a spring-mass system at two different times

boundary-value problem

a differential equation with associated boundary conditions

characteristic equation

the equation $aλ^2+bλ+c=0$ for the differential equation $ay″+by′+cy=0$

homogeneous linear equation

a second-order differential equation that can be written in the form $a_2(x)y″+a_1(x)y′+a_0(x)y=r(x)$, but $r(x)=0$ for every value of $x$

nonhomogeneous linear equation

a second-order differential equation that can be written in the form $a_2(x)y″+a_1(x)y′+a_0(x)y=r(x)$, but $r(x)≠0$ for some value of $x$

linearly dependent

a set of functions $f_1(x),\,f_2(x),\,…,\,f_n(x)$ for whichthere are constants $c_1,\,c_2,\,…,\,c_n$, not all zero, such that $c_1f_1(x)+c_2f_2(x)+⋯+c_nf_n(x)=0$ for all $x$ in the interval of interest

linearly independent

a set of functions $f_1(x),\,f_2(x),\,…,\,f_n(x)$ for which there are no constants $c_1,\,c_2,\,…,\,c_n$, such that $c_1f_1(x)+c_2f_2(x)+⋯+c_nf_n(x)=0$ for all $x$ in the interval of interest