3.3: Differentiation Rules
- Page ID
- 5465
- State the constant, constant multiple, and power rules.
- Apply the sum and difference rules to combine derivatives.
- Use the product rule for finding the derivative of a product of functions.
- Use the quotient rule for finding the derivative of a quotient of functions.
- Extend the power rule to functions with negative exponents.
- Combine the differentiation rules to find the derivative of a polynomial or rational function.
Finding derivatives of functions by using the definition of the derivative can be a lengthy and, for certain functions, a rather challenging process. For example, previously we found that
\[\dfrac{d}{dx}\left(\sqrt{x}\right)=\dfrac{1}{2\sqrt{x}} \nonumber \]
by using a process that involved multiplying an expression by a conjugate prior to evaluating a limit.
The process that we could use to evaluate \(\dfrac{d}{dx}\left(\sqrt[3]{x}\right)\) using the definition, while similar, is more complicated.
In this section, we develop rules for finding derivatives that allow us to bypass this process. We begin with the basics.
The Basic Rules
The functions \(f(x)=c\) and \(g(x)=x^n\) where \(n\) is a positive integer are the building blocks from which all polynomials and rational functions are constructed. To find derivatives of polynomials and rational functions efficiently without resorting to the limit definition of the derivative, we must first develop formulas for differentiating these basic functions.
The Constant Rule
We first apply the limit definition of the derivative to find the derivative of the constant function, \(f(x)=c\). For this function, both \(f(x)=c\) and \(f(x+h)=c\), so we obtain the following result:
\[\begin{align*} f′(x) &=\lim_{h→0} \dfrac{f(x+h)−f(x)}{h} \\[4pt] &=\lim_{h→0}\dfrac{c−c}{h} \\[4pt] &=\lim_{h→0}\dfrac{0}{h} \\[4pt] &=\lim_{h→0}0=0. \end{align*}\]
The rule for differentiating constant functions is called the constant rule. It states that the derivative of a constant function is zero; that is, since a constant function is a horizontal line, the slope, or the rate of change, of a constant function is \(0\). We restate this rule in the following theorem.
Let \(c\) be a constant. If \(f(x)=c\), then \(f′(x)=0.\)
Alternatively, we may express this rule as
\[\dfrac{d}{dx}(c)=0. \nonumber \]
Find the derivative of \(f(x)=8.\)
Solution
This is just a one-step application of the rule: \(f′(8)=0.\)
Find the derivative of \(g(x)=−3\).
- Hint
-
Use the preceding example as a guide
- Answer
-
0
The Power Rule
We have shown that
\[\dfrac{d}{dx}\left(x^2\right)=2x\quad\text{ and }\quad\dfrac{d}{dx}\left(x^{1/2}\right)=\dfrac{1}{2}x^{−1/2}. \nonumber \]
At this point, you might see a pattern beginning to develop for derivatives of the form \(\dfrac{d}{dx}\left(x^n\right)\). We continue our examination of derivative formulas by differentiating power functions of the form \(f(x)=x^n\) where \(n\) is a positive integer. We develop formulas for derivatives of this type of function in stages, beginning with positive integer powers. Before stating and proving the general rule for derivatives of functions of this form, we take a look at a specific case, \(\dfrac{d}{dx}(x^3)\). As we go through this derivation, pay special attention to the portion of the expression in boldface, as the technique used in this case is essentially the same as the technique used to prove the general case.
Find \(\dfrac{d}{dx}\left(x^3\right)\).
Solution:
| \(\displaystyle \dfrac{d}{dx}\left(x^3\right)=\lim_{h→0}\dfrac{(x+h)^3−x^3}{h}\) | |
| \(\displaystyle =\lim_{h→0}\dfrac{x^3+3x^2h+3xh^2+h^3−x^3}{h}\) | Notice that the first term in the expansion of \((x+h)^3\) is \(x^3\) and the second term is \(3x^2h\). All other terms contain powers of \(h\) that are two or greater |
| \(\displaystyle =\lim_{h→0}\dfrac{3x^2h+3xh^2+h^3}{h}\) | In this step the \(x^3\) terms have been cancelled, leaving only terms containing \(h\). |
| \(\displaystyle =\lim_{h→0}\dfrac{h(3x^2+3xh+h^2)}{h}\) | Factor out the common factor of \(h\). |
| \(\displaystyle =\lim_{h→0}(3x^2+3xh+h^2)\) | After cancelling the common factor of \(h\),the only term not containing \(h\) is \(3x^2\). |
| \(=3x^2\) | Let \(h\) go to \(0\). |
Find \(\dfrac{d}{dx}\left(x^4\right).\)
- Hint
-
Use \((x+h)^4=x^4+4x^3h+6x^2h^2+4xh^3+h^4\) and follow the procedure outlined in the preceding example.
- Answer
-
\(\dfrac{d}{dx}\left(x^4\right) = 4x^3\)
As we shall see, the procedure for finding the derivative of the general form \(f(x)=x^n\) is very similar. Although it is often unwise to draw general conclusions from specific examples, we note that when we differentiate \(f(x)=x^3\), the power on \(x\) becomes the coefficient of \(x^2\) in the derivative and the power on \(x\) in the derivative decreases by 1. The following theorem states that the power rule holds for all positive integer powers of \(x\). We will eventually extend this result to negative integer powers. Later, we will see that this rule may also be extended first to rational powers of \(x\) and then to arbitrary powers of \(x\). Be aware, however, that this rule does not apply to functions in which a constant is raised to a variable power, such as \(f(x)=3^x\).
Let \(n\) be a positive integer. If \(f(x)=x^n\),then
\[f′(x)=nx^{n−1}. \nonumber \]
Alternatively, we may express this rule as
\[\dfrac{d}{dx}\left(x^n\right)=nx^{n−1.} \nonumber \]
For \(f(x)=x^n\) where \(n\) is a positive integer, we have
\[f′(x)=\lim_{h→0}\dfrac{(x+h)^n−x^n}{h}. \nonumber \]
Since
\((x+h)^n=x^n+nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n,\)
we see that
\((x+h)^n−x^n=nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n.\)
Next, divide both sides by h:
\(\dfrac{(x+h)^n−x^n}{h}=\dfrac{nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n}{h}.\)
Thus,
\(\dfrac{(x+h)^n−x^n}{h}=nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n−1}.\)
Finally,
\[f′(x)=\lim_{h→0}(nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n-1}) \nonumber \]
\(=nx^{n−1}.\)
□
Find the derivative of the function \(f(x)=x^{10}\) by applying the power rule.
Solution
Using the power rule with \(n=10\), we obtain
\[f'(x)=10x^{10−1}=10x^9. \nonumber \]
Find the derivative of \(f(x)=x^7\).
- Hint
-
Use the power rule with \(n=7.\)
- Answer
-
\(f′(x)=7x^6\)
The Sum, Difference, and Constant Multiple Rules
We find our next differentiation rules by looking at derivatives of sums, differences, and constant multiples of functions. Just as when we work with functions, there are rules that make it easier to find derivatives of functions that we add, subtract, or multiply by a constant. These rules are summarized in the following theorem.
Let \(f(x)\) and \(g(x)\) be differentiable functions and \(k\) be a constant. Then each of the following equations holds.
Sum Rule. The derivative of the sum of a function \(f\) and a function \(g\) is the same as the sum of the derivative of \(f\) and the derivative of \(g\).
\[\dfrac{d}{dx}\big(f(x)+g(x)\big)=\dfrac{d}{dx}\big(f(x)\big)+\dfrac{d}{dx}\big(g(x)\big); \nonumber \]
that is,
\[\text{for }s(x)=f(x)+g(x),\quad s′(x)=f′(x)+g′(x). \nonumber \]
Difference Rule. The derivative of the difference of a function \(f\) and a function \(g\) is the same as the difference of the derivative of \(f\) and the derivative of \(g\) :
\[\dfrac{d}{dx}(f(x)−g(x))=\dfrac{d}{dx}(f(x))−\dfrac{d}{dx}(g(x)); \nonumber \]
that is,
\[\text{for }d(x)=f(x)−g(x),\quad d′(x)=f′(x)−g′(x). \nonumber \]
Constant Multiple Rule. The derivative of a constant \(k\) multiplied by a function \(f\) is the same as the constant multiplied by the derivative:
\[\dfrac{d}{dx}\big(kf(x)\big)=k\dfrac{d}{dx}\big(f(x)\big); \nonumber \]
that is,
\[\text{for }m(x)=kf(x),\quad m′(x)=kf′(x). \nonumber \]
We provide only the proof of the sum rule here. The rest follow in a similar manner.
For differentiable functions \(f(x)\) and \(g(x)\), we set \(s(x)=f(x)+g(x)\). Using the limit definition of the derivative we have
\[s′(x)=\lim_{h→0}\dfrac{s(x+h)−s(x)}{h}.\nonumber \]
By substituting \(s(x+h)=f(x+h)+g(x+h)\) and \(s(x)=f(x)+g(x),\) we obtain
\[s′(x)=\lim_{h→0}\dfrac{\big(f(x+h)+g(x+h)\big)−\big(f(x)+g(x)\big)}{h}.\nonumber \]
Rearranging and regrouping the terms, we have
\[s′(x)=\lim_{h→0}\left(\dfrac{f(x+h)−f(x)}{h}+\dfrac{g(x+h)−g(x)}{h}\right).\nonumber \]
We now apply the sum law for limits and the definition of the derivative to obtain
\[s′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}+\lim_{h→0}\dfrac{g(x+h)−g(x)}{h}=f′(x)+g′(x).\nonumber \]
□
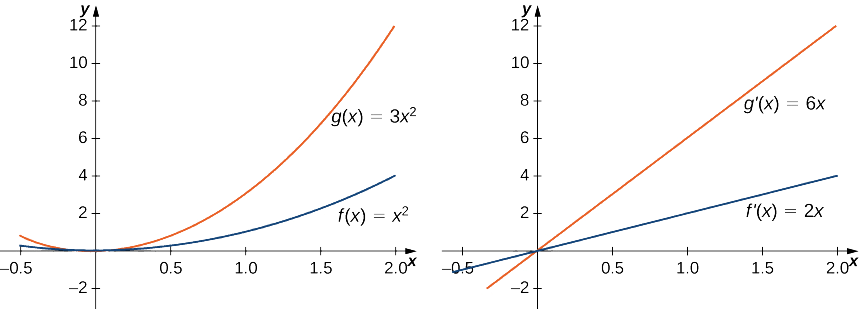
Find the derivative of \(g(x)=3x^2\) and compare it to the derivative of \(f(x)=x^2.\)
Solution
We use the power rule directly:
\[g′(x)=\dfrac{d}{dx}(3x^2)=3\dfrac{d}{dx}(x^2)=3(2x)=6x.\nonumber \]
Since \(f(x)=x^2\) has derivative \(f′(x)=2x\), we see that the derivative of \(g(x)\) is 3 times the derivative of \(f(x)\). This relationship is illustrated in Figure \(\PageIndex{1}\).
Find the derivative of \(f(x)=2x^5+7\).
Solution
We begin by applying the rule for differentiating the sum of two functions, followed by the rules for differentiating constant multiples of functions and the rule for differentiating powers. To better understand the sequence in which the differentiation rules are applied, we use Leibniz notation throughout the solution:
\(\begin{align*} f′(x)&=\dfrac{d}{dx}\left(2x^5+7\right)\\[4pt]
&=\dfrac{d}{dx}(2x^5)+\dfrac{d}{dx}(7) & & \text{Apply the sum rule.}\\[4pt]
&=2\dfrac{d}{dx}(x^5)+\dfrac{d}{dx}(7) & & \text{Apply the constant multiple rule.}\\[4pt]
&=2(5x^4)+0 & & \text{Apply the power rule and the constant rule.}\\[4pt]
&=10x^4 & & \text{Simplify.} \end{align*}\)
Find the derivative of \(f(x)=2x^3−6x^2+3.\)
- Hint
-
Use the preceding example as a guide.
- Answer
-
\(f′(x)=6x^2−12x.\)
Find the equation of the line tangent to the graph of \(f(x)=x^2−4x+6\) at \(x=1\)
Solution
To find the equation of the tangent line, we need a point and a slope. To find the point, compute
\[f(1)=1^2−4(1)+6=3. \nonumber \]
This gives us the point \((1,3)\). Since the slope of the tangent line at 1 is \(f′(1)\), we must first find \(f′(x)\). Using the definition of a derivative, we have
\[f′(x)=2x−4\nonumber \]
so the slope of the tangent line is \(f′(1)=−2\). Using the point-slope formula, we see that the equation of the tangent line is
\[y−3=−2(x−1).\nonumber \]
Putting the equation of the line in slope-intercept form, we obtain
\[y=−2x+5.\nonumber \]
Find the equation of the line tangent to the graph of \(f(x)=3x^2−11\) at \(x=2\). Use the point-slope form.
- Hint
-
Use the preceding example as a guide.
- Answer
-
\(y=12x−23\)
The Product Rule
Now that we have examined the basic rules, we can begin looking at some of the more advanced rules. The first one examines the derivative of the product of two functions. Although it might be tempting to assume that the derivative of the product is the product of the derivatives, similar to the sum and difference rules, the product rule does not follow this pattern. To see why we cannot use this pattern, consider the function \(f(x)=x^2\), whose derivative is \(f′(x)=2x\) and not \(\dfrac{d}{dx}(x)⋅\dfrac{d}{dx}(x)=1⋅1=1.\)
Let \(f(x)\) and \(g(x)\) be differentiable functions. Then
\[\dfrac{d}{dx}(f(x)g(x))=\dfrac{d}{dx}(f(x))⋅g(x)+\dfrac{d}{dx}(g(x))⋅f(x). \nonumber \]
That is,
\[\text{if }p(x)=f(x)g(x),\quad \text{then }p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
This means that the derivative of a product of two functions is the derivative of the first function times the second function plus the derivative of the second function times the first function.
We begin by assuming that \(f(x)\) and \(g(x)\) are differentiable functions. At a key point in this proof we need to use the fact that, since \(g(x)\) is differentiable, it is also continuous. In particular, we use the fact that since \(g(x)\) is continuous, \(\displaystyle \lim_{h→0}g(x+h)=g(x).\)
By applying the limit definition of the derivative to \(p(x)=f(x)g(x),\) we obtain
\[ p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x)}{h}.\nonumber \]
By adding and subtracting \(f(x)g(x+h)\) in the numerator, we have
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)+f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
After breaking apart this quotient and applying the sum law for limits, the derivative becomes
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)}{h}+\lim_{h→0}\dfrac{f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Rearranging, we obtain
\[\begin{align*}p′(x)&=\lim_{h→0}\left(\dfrac{f(x+h)−f(x)}{h}⋅g(x+h)\right)+\lim_{h→0}\left(\dfrac{g(x+h)−g(x)}{h}⋅f(x)\right)\\[4pt]
&= \left(\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}\right)⋅\left(\lim_{h→0}\;g(x+h)\right)+\left(\lim_{h→0}\dfrac{g(x+h)−g(x)}{h}\right)⋅f(x)\end{align*}\]
By using the continuity of \(g(x)\), the definition of the derivatives of \(f(x)\) and \(g(x)\), and applying the limit laws, we arrive at the product rule,
\[p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
□
For \(p(x)=f(x)g(x)\), use the product rule to find \(p′(2)\) if \(f(2)=3,\; f′(2)=−4,\; g(2)=1\), and \(g′(2)=6\).
Solution
Since \(p(x)=f(x)g(x)\), \(p′(x)=f′(x)g(x)+g′(x)f(x),\) and hence
\(p′(2)=f′(2)g(2)+g′(2)f(2)=(−4)(1)+(6)(3)=14.\)
For \(p(x)=(x^2+2)(3x^3−5x),\) find \(p′(x)\) by applying the product rule. Check the result by first finding the product and then differentiating.
Solution
If we set \(f(x)=x^2+2\) and \(g(x)=3x^3−5x\), then \(f′(x)=2x\) and \(g′(x)=9x^2−5\). Thus,
\(p′(x)=f′(x)g(x)+g′(x)f(x)=(2x)(3x^3−5x)+(9x^2−5)(x^2+2).\)
Simplifying, we have
\[p′(x)=15x^4+3x^2−10. \nonumber \]
To check, we see that \(p(x)=3x^5+x^3−10x\) and, consequently, \(p′(x)=15x^4+3x^2−10.\)
Use the product rule to obtain the derivative of \(p(x)=2x^5(4x^2+x).\)
- Hint
-
Set \(f(x)=2x^5\) and \(g(x)=4x^2+x\) and use the preceding example as a guide.
- Answer
-
\(p′(x)=10x^4(4x^2+x)+(8x+1)(2x^5)=56x^6+12x^5.\)
The Quotient Rule
Having developed and practiced the product rule, we now consider differentiating quotients of functions. As we see in the following theorem, the derivative of the quotient is not the quotient of the derivatives; rather, it is the derivative of the function in the numerator times the function in the denominator minus the derivative of the function in the denominator times the function in the numerator, all divided by the square of the function in the denominator. In order to better grasp why we cannot simply take the quotient of the derivatives, keep in mind that
\[\dfrac{d}{dx}(x^2)=2x,\text{ not }\dfrac{\dfrac{d}{dx}(x^3)}{\dfrac{d}{dx}(x)}=\dfrac{3x^2}{1}=3x^2.\nonumber \]
Let \(f(x)\) and \(g(x)\) be differentiable functions. Then
\[\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{\dfrac{d}{dx}(f(x))⋅g(x)−\dfrac{d}{dx}(g(x))⋅f(x)}{\big(g(x)\big)^2}. \nonumber \]
That is, if
\[q(x)=\dfrac{f(x)}{g(x)}\nonumber \]
then
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}.\nonumber \]
The proof of the quotient rule is very similar to the proof of the product rule, so it is omitted here. Instead, we apply this new rule for finding derivatives in the next example.
Use the quotient rule to find the derivative of \(q(x)=\dfrac{5x^2}{4x+3}.\)
Solution
Let \(f(x)=5x^2\) and \(g(x)=4x+3\). Thus, \(f′(x)=10x\) and \(g′(x)=4\).
Substituting into the quotient rule, we have
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{(g(x))^2}=\dfrac{10x(4x+3)−4(5x^2)}{(4x+3)^2}.\nonumber \]
Simplifying, we obtain
\[q′(x)=\dfrac{20x^2+30x}{(4x+3)^2}\nonumber \]
Find the derivative of \(h(x)=\dfrac{3x+1}{4x−3}\).
- Hint
-
Apply the quotient rule with \(f(x)=3x+1\) and \(g(x)=4x−3\).
- Answer
-
\(h′(x)=−\dfrac{13}{(4x−3)^2}.\)
It is now possible to use the quotient rule to extend the power rule to find derivatives of functions of the form \(x^k\) where \(k\) is a negative integer.
If \(k\) is a negative integer, then
\[\dfrac{d}{dx}(x^k)=kx^{k−1}. \nonumber \]
If \(k\) is a negative integer, we may set \(n=−k\), so that n is a positive integer with \(k=−n\). Since for each positive integer \(n\),\(x^{−n}=\dfrac{1}{x^n}\), we may now apply the quotient rule by setting \(f(x)=1\) and \(g(x)=x^n\). In this case, \(f′(x)=0\) and \(g′(x)=nx^{n−1}\). Thus,
\[\dfrac{d}{dx}(x^{−n})=\dfrac{0(x^n)−1(nx^{n−1})}{(x^n)^2}.\nonumber \]
Simplifying, we see that
\[\begin{align*} \dfrac{d}{dx}(x^{−n}) &=\dfrac{−nx^{n−1}}{x^{2n}}\\[4pt]&=−nx^{(n−1)−2n}\\[4pt]&=−nx^{−n−1}.\end{align*}\]
Finally, observe that since \(k=−n\), by substituting we have
\[\dfrac{d}{dx}(x^k)=kx^{k−1}.\nonumber \]
□
Find \(\dfrac{d}{dx}(x^{−4})\).
Solution
By applying the extended power rule with \(k=−4\), we obtain
\[\dfrac{d}{dx}(x^{−4})=−4x^{−4−1}=−4x^{−5}.\nonumber \]
Use the extended power rule and the constant multiple rule to find \(f(x)=\dfrac{6}{x^2}\).
Solution
It may seem tempting to use the quotient rule to find this derivative, and it would certainly not be incorrect to do so. However, it is far easier to differentiate this function by first rewriting it as \(f(x)=6x^{−2}\).
\(\begin{align*} f′(x)&=\dfrac{d}{dx}\left(\dfrac{6}{x^2}\right)=\dfrac{d}{dx}\left(6x^{−2}\right) & & \text{Rewrite }\dfrac{6}{x^2}\text{ as }6x^{−2}.\\[4pt]
&=6\dfrac{d}{dx}\left(x^{−2}\right) & & \text{Apply the constant multiple rule.}\\[4pt]
&=6(−2x^{−3}) & & \text{Use the extended power rule to differentiate }x^{−2}.\\[4pt]
&=−12x^{−3} & & \text{Simplify.} \end{align*} \)
Find the derivative of \(g(x)=\dfrac{1}{x^7}\) using the extended power rule.
- Hint
-
Rewrite \(g(x)=\dfrac{1}{x^7}=x^{−7}\). Use the extended power rule with \(k=−7\).
- Answer
-
\(g′(x)=−7x^{−8}\).
Combining Differentiation Rules
As we have seen throughout the examples in this section, it seldom happens that we are called on to apply just one differentiation rule to find the derivative of a given function. At this point, by combining the differentiation rules, we may find the derivatives of any polynomial or rational function. Later on we will encounter more complex combinations of differentiation rules. A good rule of thumb to use when applying several rules is to apply the rules in reverse of the order in which we would evaluate the function.
For \(k(x)=3h(x)+x^2g(x)\), find \(k′(x)\).
Solution: Finding this derivative requires the sum rule, the constant multiple rule, and the product rule.
| \(k′(x)=\dfrac{d}{dx}\big(3h(x)+x^2g(x)\big)=\dfrac{d}{dx}\big(3h(x)\big)+\dfrac{d}{dx}\big(x^2g(x)\big)\) | Apply the sum rule. |
| \(=3\dfrac{d}{dx}\big(h(x)\big)+\left(\dfrac{d}{dx}(x^2)g(x)+\dfrac{d}{dx}(g(x))x^2\right)\) | Apply the constant multiple rule to differentiate \(3h(x)\) and the product rule to differentiate \(x^2g(x)\). |
| \(=3h′(x)+2xg(x)+g′(x)x^2\) |
For \(k(x)=f(x)g(x)h(x)\), express \(k′(x)\) in terms of \(f(x),g(x),h(x)\), and their derivatives.
Solution
We can think of the function \(k(x)\) as the product of the function \(f(x)g(x)\) and the function \(h(x)\). That is, \(k(x)=(f(x)g(x))⋅h(x)\). Thus,
\(\begin{align*} k′(x)&=\dfrac{d}{dx}\big(f(x)g(x)\big)⋅h(x)+\dfrac{d}{dx}\big(h(x)\big)⋅\big(f(x)g(x)\big). & & \text{Apply the product rule to the product of }f(x)g(x)\text{ and }h(x).\\[4pt]
&=\big(f′(x)g(x)+g′(x)f(x)\big)h(x)+h′(x)f(x)g(x) & & \text{Apply the product rule to }f(x)g(x)\\[4pt]
&=f′(x)g(x)h(x)+f(x)g′(x)h(x)+f(x)g(x)h′(x). & & \text{Simplify.}\end{align*} \)
For \(h(x)=\dfrac{2x^3k(x)}{3x+2}\), find \(h′(x)\).
Solution
This procedure is typical for finding the derivative of a rational function.
\(\begin{align*} h′(x)&=\dfrac{\dfrac{d}{dx}(2x^3k(x))⋅(3x+2)−\dfrac{d}{dx}(3x+2)⋅(2x^3k(x))}{(3x+2)^2} & & \text{Apply the quotient rule.}\\[4pt]
&=\dfrac{(6x^2k(x)+k′(x)⋅2x^3)(3x+2)−3(2x^3k(x))}{(3x+2)^2} & & \text{Apply the product rule to find }\dfrac{d}{dx}(2x^3k(x)). \text{ Use }\dfrac{d}{dx}(3x+2)=3.\\[4pt]
&=\dfrac{−6x^3k(x)+18x^3k(x)+12x^2k(x)+6x^4k′(x)+4x^3k′(x)}{(3x+2)^2} & & \text{Simplify} \end{align*} \)
Find \(\dfrac{d}{dx}(3f(x)−2g(x)).\)
- Hint
-
Apply the difference rule and the constant multiple rule.
- Answer
-
\(3f′(x)−2g′(x).\)
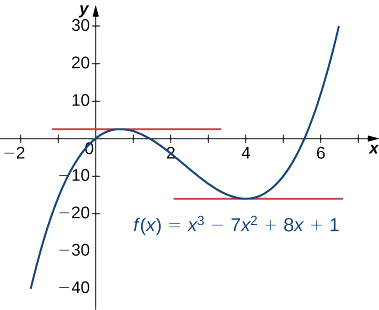
Determine the values of \(x\) for which \(f(x)=x^3−7x^2+8x+1\) has a horizontal tangent line.
Solution
To find the values of \(x\) for which \(f(x)\) has a horizontal tangent line, we must solve \(f′(x)=0\).
Since \(f′(x)=3x^2−14x+8=(3x−2)(x−4)\),
we must solve \((3x−2)(x−4)=0\). Thus we see that the function has horizontal tangent lines at \(x=\dfrac{2}{3}\) and \(x=4\) as shown in the following graph.
The position of an object on a coordinate axis at time \(t\) is given by \(s(t)=\dfrac{t}{t^2+1}.\) What is the initial velocity of the object?
Solution
Since the initial velocity is \(v(0)=s′(0),\) begin by finding \(s′(t)\) by applying the quotient rule:
\(s′(t)=\dfrac{1(t^2+1)−2t(t)}{(t^2+1)^2}=\dfrac{1−t^2}{(t^2+1)^2}\).
After evaluating, we see that \(v(0)=1.\)
Find the values of \(x\) for which the line tangent to the graph of \(f(x)=4x^2−3x+2\) has a tangent line parallel to the line \(y=2x+3.\)
- Hint
-
Solve \(f′(x)=2\).
- Answer
-
\(\dfrac{5}{8}\)
Formula One car races can be very exciting to watch and attract a lot of spectators. Formula One track designers have to ensure sufficient grandstand space is available around the track to accommodate these viewers. However, car racing can be dangerous, and safety considerations are paramount. The grandstands must be placed where spectators will not be in danger should a driver lose control of a car (Figure \(\PageIndex{3}\)).

Safety is especially a concern on turns. If a driver does not slow down enough before entering the turn, the car may slide off the racetrack. Normally, this just results in a wider turn, which slows the driver down. But if the driver loses control completely, the car may fly off the track entirely, on a path tangent to the curve of the racetrack.
Suppose you are designing a new Formula One track. One section of the track can be modeled by the function \(f(x)=x^3+3x^2+x\) (Figure \(\PageIndex{4}\)). The current plan calls for grandstands to be built along the first straightaway and around a portion of the first curve. The plans call for the front corner of the grandstand to be located at the point (\(−1.9,2.8\)). We want to determine whether this location puts the spectators in danger if a driver loses control of the car.
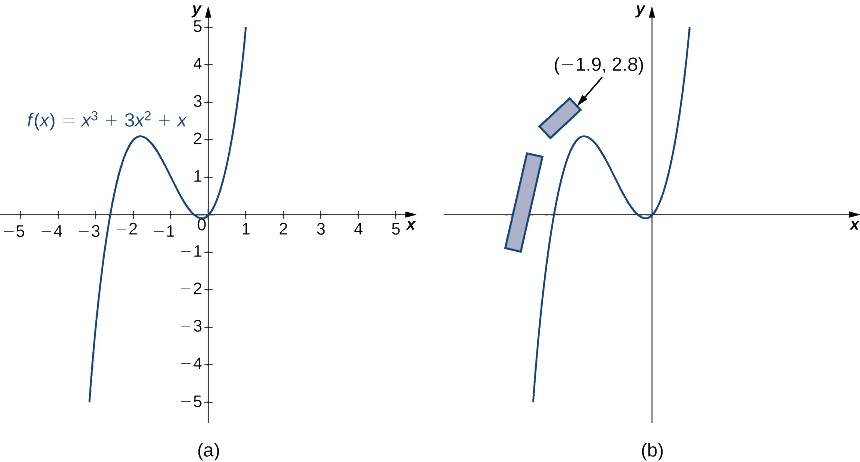
- Physicists have determined that drivers are most likely to lose control of their cars as they are coming into a turn, at the point where the slope of the tangent line is 1. Find the \((x,y)\) coordinates of this point near the turn.
- Find the equation of the tangent line to the curve at this point.
- To determine whether the spectators are in danger in this scenario, find the \(x\)-coordinate of the point where the tangent line crosses the line \(y=2.8\). Is this point safely to the right of the grandstand? Or are the spectators in danger?
- What if a driver loses control earlier than the physicists project? Suppose a driver loses control at the point (\(−2.5,0.625\)). What is the slope of the tangent line at this point?
- If a driver loses control as described in part 4, are the spectators safe?
- Should you proceed with the current design for the grandstand, or should the grandstands be moved?
Key Concepts
- The derivative of a constant function is zero.
- The derivative of a power function is a function in which the power on \(x\) becomes the coefficient of the term and the power on \(x\) in the derivative decreases by 1.
- The derivative of a constant \(c\) multiplied by a function \(f\) is the same as the constant multiplied by the derivative.
- The derivative of the sum of a function \(f\) and a function \(g\) is the same as the sum of the derivative of \(f\) and the derivative of \(g\).
- The derivative of the difference of a function \(f\) and a function \(g\) is the same as the difference of the derivative of \(f\) and the derivative of \(g\).
- The derivative of a product of two functions is the derivative of the first function times the second function plus the derivative of the second function times the first function.
- The derivative of the quotient of two functions is the derivative of the first function times the second function minus the derivative of the second function times the first function, all divided by the square of the second function.
- We used the limit definition of the derivative to develop formulas that allow us to find derivatives without resorting to the definition of the derivative. These formulas can be used singly or in combination with each other.
Glossary
- constant multiple rule
- the derivative of a constant \(c\) multiplied by a function \(f\) is the same as the constant multiplied by the derivative: \(\dfrac{d}{dx}\big(cf(x)\big)=cf′(x)\)
- constant rule
- the derivative of a constant function is zero: \(\dfrac{d}{dx}(c)=0\), where \(c\) is a constant
- difference rule
- the derivative of the difference of a function \(f\) and a function \(g\) is the same as the difference of the derivative of \(f\) and the derivative of \(g\): \(\dfrac{d}{dx}\big(f(x)−g(x)\big)=f′(x)−g′(x)\)
- power rule
- the derivative of a power function is a function in which the power on \(x\) becomes the coefficient of the term and the power on \(x\) in the derivative decreases by 1: If \(n\) is an integer, then \(\dfrac{d}{dx}\left(x^n\right)=nx^{n−1}\)
- product rule
- the derivative of a product of two functions is the derivative of the first function times the second function plus the derivative of the second function times the first function: \(\dfrac{d}{dx}\big(f(x)g(x)\big)=f′(x)g(x)+g′(x)f(x)\)
- quotient rule
- the derivative of the quotient of two functions is the derivative of the first function times the second function minus the derivative of the second function times the first function, all divided by the square of the second function: \(\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}\)
- sum rule
- the derivative of the sum of a function \(f\) and a function \(g\) is the same as the sum of the derivative of \(f\) and the derivative of \(g\): \(\dfrac{d}{dx}\big(f(x)+g(x)\big)=f′(x)+g′(x)\)

