Stokes' Theorem II

Stokes' Theorem

The divergence theorem is used to find a surface integral over a closed surface and Green's theorem is use to find a line integral that encloses a surface (region) in the xy-plane. The theorem of the day, Stokes' theorem relates the surface integral to a line integral. Since we will be working in three dimensions, we need to discus what it means for a curve to be oriented positively.

Let S be a oriented surface with unit normal vector N and let C be the boundary of S. Then C is positively oriented if its orientation follows the right hand rule, that is if you right hand curls around N in the direction of C's orientation, then your thumb will be pointing in the direction of N.

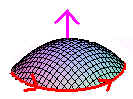
Now we are ready to state Stokes' Theorem. The proof will be left for a more advanced course.

Theorem: Stoke's Theorem

Let S be an oriented surface with unit normal vector N and C be the positively oriented boundary of S. If F is a vector field with continuous first order partial derivatives then

$$\int_C F \cdot d \textbf{r} = \iint_S (Curl\; F) \cdot N dS \nonumber$$

Example $\PageIndex{1}$

Let S be the part of the plane

$$z=4-x-2y \nonumber$$

with upwardly pointing unit normal vector.

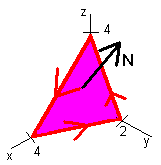
Use Stokes' theorem to find

$$\int_C F \cdot d\textbf{r} \nonumber$$

Where

$$\textbf{F} = y \hat{\textbf{i}} + z \hat{\textbf{j}} - xy \hat{\textbf{k}} \nonumber$$

Solution

First notice that without Stokes' theorem, we would have to parameterize three different line segments. Instead we can find this with just one double integral.

We have

$$Curl \textbf{F} = \begin{vmatrix} \hat{\textbf{i}} &\hat{\textbf{j}} &\hat{\textbf{k}} \\ \partial x & \partial y & \partial z \\ y &z &-xy \end{vmatrix} = (1+x) \hat{\textbf{i}} + y \hat{\textbf{j}} - \hat{\textbf{k}} \nonumber$$

and

$$\textbf{N} dS = \hat{\textbf{i}} + 2 \hat{\textbf{j}} + \hat{\textbf{k}} \nonumber$$

So that

$$Curl F \cdot N dS = 1+x+2y -1 = x+2y\nonumber$$

We integrate

$$\int_0^4 \int_0^{2-\frac{1}{2}x} (x+2y)dydx = \dfrac{32}{3} \nonumber$$

Curl and Circulation

Just as the divergence theorem assisted us in understanding the divergence of a function at a point, Stokes' theorem helps us understand what the Curl of a vector field is. Let P be a point on the surface and C_e be a tiny circle around P on the surface. Then

$$\int_{C_e} \textbf{F} \cdot dr \nonumber$$

measures the amount of circulation around P. You can see this by noticing that if F flows in the direction of the tangent vector, then $\textbf{F} \cdot d \textbf{r}$ will be positive. If it flows in the opposite direction, then it will be negative. The stronger the force field in the direction of the tangent vector, the greater the circulation.

Since the region enclosed by C_e is tiny, the surface integral can be approximated by

$$\iint_S (Curl \; \textbf{F}) \cdot N dS \approx Curl \textbf{F}(P)\cdot \textbf{N} (\text{Area of C}) \nonumber$$

or

$$Curl \; \textbf{F} \cdot N = \text{Circulation per unit area} \nonumber$$

So the curl tell us how much the force field rotates around the point.

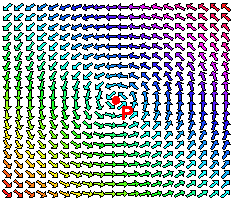
We can see that if this is a small piece of the surface containing P, then

$$Curl \; F \cdot N > 0 \nonumber$$

Contributors and Attributions

• Larry Green (Lake Tahoe Community College)