4.4.E: Green's Theorem (Exercises)
- Page ID
- 78232
Exercise \(\PageIndex{1}\)
Let \(D\) be the closed rectangle in \(\mathbb{R}^2\) with vertices at (0,0), (2,0), (2,4), and (0,4), with boundary \(\partial D\) oriented counterclockwise. Use Green’s theorem to evaluate the following line integrals.
(a) \(\int_{\partial D} 2 x y d x+3 x^{2} d y\)
(b) \(\int_{\partial D} y d x+x d y\)
- Answer
-
(a) \(\int_{\partial D} 2 x y d x+3 x^{2} d y=80\)
Exercise \(\PageIndex{2}\)
Let \(D\) be the triangle in \(\mathbb{R}^2\) with vertices at (0,0), (2,0), and (0,4), with boundary \(\partial D\) oriented counterclockwise. Use Green’s theorem to evaluate the following line integrals.
(a) \(\int_{\partial D} 2 x y^{2} d x+4 x d y\)
(b) \(\int_{\partial D} y d x+x d y\)
(c) \(\int_{\partial D} y d x-x d y\)
- Answer
-
(a) \(\int_{\partial D} 2 x y^{2} d x+4 x d y=\frac{16}{3} \text { (c) } \int_{\partial D} y d x-x d y=-8\)
Exercise \(\PageIndex{3}\)
Use Green’s theorem to find the area of a circle of radius \(r\).
Exercise \(\PageIndex{4}\)
Use Green’s theorem to find the area of the region \(D\) enclosed by the hypocycloid
\[ x^{\frac{2}{3}}+y^{\frac{2}{3}}=a^{\frac{2}{3}} , \nonumber \]
where \(a > 0\). Note that we may parametrize this curve using
\[ \varphi(t)=\left(a \cos ^{3}(t), a \sin ^{3}(t)\right) , \nonumber \]
\(0 \leq t \leq 2 \pi\).
- Answer
-
\(\frac{3}{8} \pi a^{2}\)
Exercise \(\PageIndex{5}\)
Use Green’s theorem to find the area of the region enclosed by one “petal” of the curve parametrized by
\[ \varphi(t)=(\sin (2 t) \cos (t), \sin (2 t) \sin (t)) . \nonumber \]
- Answer
-
\(\frac{\pi}{8}\)
Exercise \(\PageIndex{6}\)
Find the area of the region enclosed by the cardioid parametrized by
\[ \varphi(t)=((2+\cos (t)) \cos (t),(2+\cos (t)) \sin (t)) , \nonumber \]
\(0 \leq t \leq 2 \pi\).
- Answer
-
\(\frac{9 \pi}{2}\)
Exercise \(\PageIndex{7}\)
Verify (4.4.23), thus completing the proof of Green’s theorem.
Exercise \(\PageIndex{8}\)
Suppose the vector field \(F: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}\) with coordinate functions \(p=F_{1}(x, y)\) and \(q=F_{2}(x, y)\) is \(C^1\) on an open set containing the Type III region \(D\). Moreover, suppose \(F\) is the gradient of a scalar function \(f: \mathbb{R}^{2} \rightarrow \mathbb{R}\).
(a) Show that
\[ \frac{\partial q}{\partial x}-\frac{\partial p}{\partial y}=0 \nonumber \]
for all points \((x,y)\) in \(D\).
(b) Use Green’s theorem to show that
\[ \int_{\partial D} p d x+q d y=0 , \nonumber \]
where \(\partial D\) is the boundary of \(D\) with counterclockwise orientation.
Exercise \(\PageIndex{9}\)
How many ways do you know to calculate the area of a circle?
Exercise \(\PageIndex{10}\)
Who was George Green?
Exercise \(\PageIndex{11}\)
Explain how Green’s theorem is a generalization of the Fundamental Theorem of Integral Calculus.
Exercise \(\PageIndex{12}\)
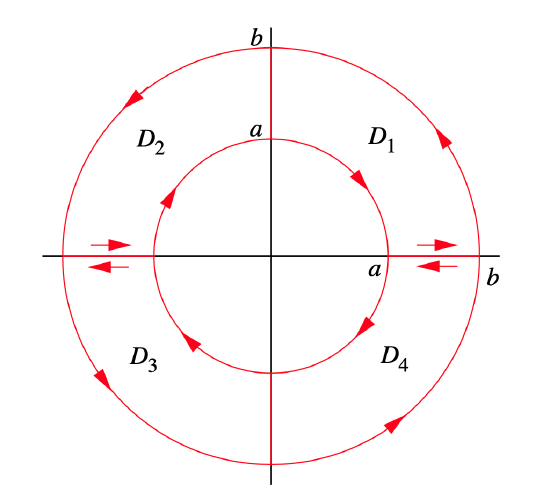
Let \(b > a\), let \(C_1\) be the circle of radius \(b\) centered at the origin, and let \(C_2\) be the circle of radius \(a\) centered at the origin. If \(D\) is the annular region between \(C_1\) and \(C_2\) and \(F\) is a \(C^1\) vector field with coordinate functions \(p=F_{1}(x, y)\) and \(q=F_{2}(x, y)\), show that
\[ \iint_{D}\left(\frac{\partial q}{\partial x}-\frac{\partial p}{\partial y}\right) d x d y=\int_{C_{1}} p d x+q d y+\int_{C_{2}} p d x+q d y , \nonumber \]
where \(C_1\) is oriented in the counterclockwise direction and \(C_2\) is oriented in the clockwise direction. (Hint: Decompose \(D\) into Type III regions \(D_1\), \(D_2\), \(D_3\), and \(D_4\), each with boundary oriented counterclockwise, as shown in Figure 4.4.5.)