7.1: Definition of Relations
- Page ID
- 8421
Given two nonempty sets \(A\) and \(B\), a function tells us how to obtain a unique element \(b\in B\) from any element \(a\in A\). Very often, we are only interested in some sort of relationship between the elements from these two sets. A familiar example is the equality of two numbers. By saying \(a=b\), we are proclaiming that the two numbers \(a\) and \(b\) are related by being equal in value. Likewise, \(a\geq b\) is another example of a relation.
Example \(\PageIndex{1}\label{eg:defnrelat-01}\)
Given \(a, b\in\mathbb{R}^*\), declare \(a\) and \(b\) to be related if they have the same sign. For instance, \(7.14\) and \(e\) are related, so are \(-\pi\) and \(-\sqrt{2}\). However, 5 and \(-2\) are not. Note that \(a\) is related to \(b\) implies that \(b\) is also related to \(a\).
Example \(\PageIndex{2}\label{eg:defnrelat-02}\)
For \(a,b\in\mathbb{R}\), define “\(a\) is related to \(b\)” if and only if \(a<b\). Take note that \(3<5\), but \(5\nless3\). This demonstrates that \(a\) is related to \(b\) does not necessarily imply that \(b\) is also related to \(a\).
Example \(\PageIndex{3}\label{eg:defnrelat-03}\)
Let \(A\) be a set of students, and let \(B\) be a set of courses. Given \(a\in A\) and \(b\in B\), define “\(a\) is related to \(b\)” if and only if student \(a\) is taking course \(b\). While it could be possible that “John Smith is related to MATH 210” because John is taking MATH 210, it is certainly absurd to say that “MATH 210 is related to John Smith,” because it does not make much sense to say that MATH 210 is taking John Smith. This again illustrates that \(a\) is related to \(b\) does not necessarily imply that \(b\) is also related to \(a\).
In these examples, we see that when we say “\(a\) is related to \(b\),” the order in which \(a\) and \(b\) appear may make a difference. This suggests the following definition.
Definition
A relation from a set \(A\) to a set \(B\) is a subset of \(A \times B\). Hence, a relation \(R\) consists of ordered pairs \((a,b)\), where \(a\in A\) and \(b\in B\). If \((a,b)\in R\), we say that is related to , and we also write \(a\,R\,b\).
Remark
We can also replace \(R\) by a symbol, especially when one is readily available. This is exactly what we do in, for example, \(a<b\). To say it is not true that \(a<b\), we can write \(a\nless b\). Likewise, if \((a,b)\notin R\), then \(a\) is not related to \(b\), and we could write \(a\!\not\!R\,b\). But the slash may not be easy to recognize when it is written over an uppercase letter. In this regard, it may be a good practice to avoid using the slash notation over a letter. Alternatively, one may use the “bar” notation \(\overline{a\,R\,b}\) to indicate that \(a\) and \(b\) are not related.
Example \(\PageIndex{4}\label{eg:defnrelat-04}\)
Define \(R=\{(a,b)\in\mathbb{R}^2 \mid a<b \}\), hence \((a,b)\in R\) if and only if \(a<b\). Obviously, saying “\(a<b\)” is much clearer than “\(a\,R\,b\).” If \(a\) and \(b\) are not related, we could say \((a,b)\notin R\), or \(a\nless b\).
Example \(\PageIndex{5}\label{eg:defnrelat-05}\)
Define \[F = \left\{(x,y)\in\mathbb{R}^2 \biggm| y=\frac{1}{x^2+1} \right\}. \nonumber\] Therefore \(x\) is related to \(y\) if and only if \(y=\frac{1}{x^2+1}\). We can also write \[F = \left\{\left(x,\frac{1}{x^2+1}\right) \biggm| x\in\mathbb{R} \right\}, \nonumber\] which may look a bit simpler.
For instance, \((1,0.5)\in F\), but \((1,0)\not\in F\). In this case, \((2,0.2)\in F\) is probably easier to understand than \(2\,F\,0.2\). Likewise, \((1,2)\notin F\) may be easier to read than \(1\!\not\!F\,2\).
hands-on Exercise \(\PageIndex{1}\label{he:defnrelat-01}\)
Define the relation \(H\) as \(\{(x,x^2+1)\mid x\in\mathbb{R}\}\). Determine whether the following statements \[\textstyle 2\,H\,3, \quad (-4,17)\notin H, \quad \big(\frac{1}{2},\frac{3}{2}\big)\notin H, \quad (\sqrt{2},3)\in H, \quad (1,2)\in H, \nonumber\] are true or false.
hands-on Exercise \(\PageIndex{2}\label{he:defnrelat-02}\)
Let \(G=\{(x,y)\in\mathbb{R}^2 \mid xy=1\}\). Is 2 related to 0.5? How would you write it? Repeat with 4 and 0.5, and with 10 and 3.
hands-on Exercise \(\PageIndex{3}\label{he:defnrelat-03}\)
In the last example, is 0 related to 3? How would you write it? Repeat with 1 and \(-1\). Again with \(\frac{1}{\sqrt{2}}\) and \(\sqrt{2}\).
Since a relation is a set, we can describe a relation by listing its elements (that is, using the roster method).
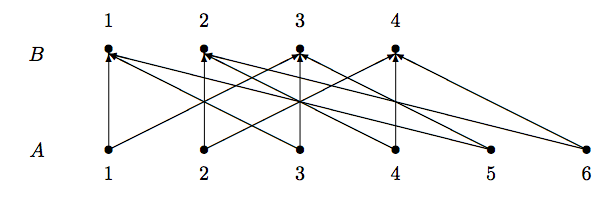
Example \(\PageIndex{6}\label{eg:parity}\)
Let \(A=\{1,2,3,4,5,6\}\) and \(B=\{1,2,3,4\}\). Define \((a,b)\in R\) if and only if \((a-b)\bmod 2 = 0\). Then \[R=\{(1,1), (1,3), (2,2), (2,4), (3,1), (3,3), (4,2), (4,4), (5,1), (5,3), (6,2), (6,4)\}. \nonumber\] We note that \(R\) consists of ordered pairs \((a,b)\) where \(a\) and \(b\) have the same parity. Be cautious, that \(1\leq a\leq 6\) and \(1\leq b\leq 4\). Hence, it is meaningless to talk about whether \((1,5)\in R\) or \((1,5)\notin R\).
hands-on Exercise \(\PageIndex{4}\label{he:relat-div}\)
Let \(A=\{2,3,4,7\}\) and \(B=\{1,2,3,\ldots,12\}\). Define \(a\,S\,b\) if and only if \(a\mid b\). Use the roster method to describe \(S\).
In the last example, 7 never appears as the first element (in the first coordinate) of any ordered pair. Likewise, 1, 5, 7, and 11 never appear as the second element (in the second coordinate) of any ordered pair.
Definition
The domain of a relation \(R\subseteq A\times B\) is defined as \[\mbox{dom}\,R = \{ a\in A \mid (a,b)\in R \mbox{ for some $b\in B$} \}, \nonumber\] and the image or range is defined as \[\mathrm{ im }{R} = \{ b\in B \mid (a,b)\in R \mbox{ for some $a\in A$} \}. \nonumber\]
hands-on Exercise \(\PageIndex{5}\label{he:defnrelat-05}\)
Find \(\mbox{dom}\,S\) and \(\mathrm{ im }{S}\), where \(S\) in Hands-On Exercise 7.1.4.
A relation \(R\subseteq A\times B\) can be displayed graphically on a digraph which is also called a directed graph. Represent the elements from \(A\) and \(B\) by vertices or dots, and use directed lines (also called directed edges or arcs) to connect two vertices if the corresponding elements are related. Figure \(\PageIndex{1}\) displays a graphical representation of the relation in Example 7.1.6.
Although a digraph gives us a clear and precise visual representation of a relation, it could become very confusing and hard to read when the relation contains many ordered pairs. As we will see in Section 4, we can sometimes simplify the digraphs in some special situations. Otherwise, the graphical representation is only effective for relations with a small number of ordered pairs.
We can use a matrix representation to describe a relation. A matrix consists of values arranged in rows and columns. A relation \(R\) from \(A=\{a_1,\ldots, a_m\}\) to \(B=\{b_1,\ldots,b_n\}\) can be described by an \(m\)-by-\(n\) matrix \(M=(m_{ij})\) whose entry at row \(i\) and column \(j\) is defined by \[m_{ij} = \cases{ 1 & if $a_i\,R\,b_j$, \cr 0 & otherwise. \cr} \nonumber\] The matrix \(M\) is called the incidence matrix for \(R\).
Example \(\PageIndex{7}\label{eg:defnrelat-07}\)
The incidence matrix for the relation \(R\) in Example 7.1.6 is \[\begin{array}{cc} & \begin{array}{cccc} 1 & 2 & 3 & 4 \end{array} \\ \begin{array}{c} 1 \\ 2 \\ 3 \\ 4 \\ 5 \\ 6 \end{array} & \left(\begin{array}{cccc} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \end{array}\right) \end{array} \nonumber\] in which we label the rows and columns with the elements involved in the relation.
hands-on Exercise \(\PageIndex{6}\label{he:defnrelat-06}\)
Determine the incidence matrix for the relation \(S\) in Hands-On Exercise 7.1.4.
hands-on Exercise \(\PageIndex{7}\label{he:defnrelat-07}\)
The courses taken by John, Mary, Paul, and Sally are listed below.
| John: | MATH 210, CSIT 121, MATH 223 |
| Mary: | MATH 231, CSIT 121, MATH 210 |
| Paul: | CSIT 120, MATH 231, MATH 223 |
| Sally: | MATH 210, CSIT 120 |
Represent, using a graph and a matrix, the relation \(R\) defined as \(a\,R\,b\) if student \(a\) is taking course \(b\).
Summary and Review
- Relations are generalizations of functions. A relation merely states that the elements from two sets \(A\) and \(B\) are related in a certain way.
- More formally, a relation is defined as a subset of \(A\times B\).
- The domain of a relation is the set of elements in \(A\) that appear in the first coordinates of some ordered pairs, and the image or range is the set of elements in \(B\) that appear in the second coordinates of some ordered pairs.
- For brevity and for clarity, we often write \(x\,R\,y\) if \((x,y)\in R\).
- Under this convention, the mathematical notations \(\leq\), \(\geq\), \(=\), \(\subseteq\), and their like, can be regarded as relational operators.
Exercise \(\PageIndex{1}\label{ex:defnrelat-01}\)
Represent each of the following relations from \(\{1,2,3,6\}\) to \(\{1,2,3,6\}\) using a digraph and an incidence matrix.
- \(\{(x,y)\mid x = y\}\)
- \(\{(x,y)\mid x\neq y\}\)
- \(\{(x,y)\mid x < y\}\)
Exercise \(\PageIndex{2}\label{ex:defnrelat-02}\)
Find the domain and image of each relation in Problem 7.1.1.
Exercise \(\PageIndex{3}\label{ex:defnrelat-03}\)
Represent each of the following relations from \(\{1,2,3,6\}\) to \(\{1,2,3,6\}\) using a digraph and an incidence matrix.
- \(\{(x,y)\mid x^2\leq y\}\)
- \(\{(x,y) \mid x \) divides \(y \}\)
- \(\{(x,y) \mid x + y\) is even\(\}\)
Exercise \(\PageIndex{4}\label{ex:defnrelat-04}\)
Find the domain and image of each relation in Problem 7.1.3.
Exercise \(\PageIndex{5}\label{ex:defnrelat-05}\)
Find the incidence matrix for each of the following relations from \(\{1,2,3,4\}\) to \(\{1,2,3,4,5\}\).
- \(R=\{(1,1),(2,2),(2,3),(3,3),(3,4),(4,5)\}\)
- \(S=\{(1,1),(1,2),(2,2),(2,3),(3,3),(3,4),(4,4)\}\)
- \(T=\{(1,5),(2,4),(3,3),(4,1),(4,4)\}\)
Exercise \(\PageIndex{6}\label{ex:defnrelat-06}\)
Determine the incidence matrix and the digraph that represent the relation \(R\) defined on \(\{x\in\mathbb{Z} \mid -3\leq x\leq3\}\) by \[x\,R\,y \Leftrightarrow 3\mid(x-y). \nonumber\]
Exercise \(\PageIndex{7}\label{ex:defnrelat-07}\)
Determine the incidence matrix and the digraph that represent the relation \(S\) defined on \(\{1,2,4,5,10,20\}\) by \[x\,S\,y \Leftrightarrow \mbox{($x<y$ and $x$ divides $y$)}. \nonumber\]
Exercise \(\PageIndex{8}\label{ex:defnrelat-08}\)
Let \(D=\{1,2,3,\ldots,30\}\) be the set of dates in November, and let \(W=\{\)Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday\(\}\) be the set of days of the week. For November of this year, define the relation \(T\) from \(D\) to \(W\) by \[(x,y)\in T \Leftrightarrow \mbox{$x$ falls on $y$}. \nonumber\] List the ordered pairs in \(T\). Is \(T\) a function from \(T\) to \(W\)?
Exercise \(\PageIndex{9}\label{ex:defnrelat-09}\)
Find the incidence matrix for the relation \(I\subseteq \wp(\{1,2\}) \times \wp(\{1,2\})\), where \[(S,T)\in I \Leftrightarrow S\cap T\neq\emptyset. \nonumber\]
Exercise \(\PageIndex{10}\label{ex:defnrelat-10}\)
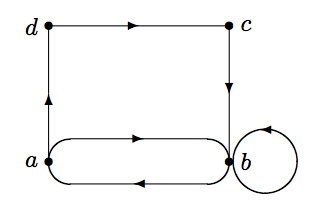
For a relation \(R\subseteq A\times A\), instead of using two rows of vertices in a digraph, we can use a digraph on the vertices that represent the elements of \(A\). Hence, it is possible to have two directed arcs between a pair of vertices, and a loop may appear around a vertex \(x\) if \((x,x)\in R\). Find the incidence matrix for the relation represented by the following digraph: