1.1: Prelude to Fundamentals
- Page ID
- 7233
Combinatorics is often described briefly as being about counting, and indeed counting is a large part of combinatorics. As the name suggests, however, it is broader than this: it is about combining things. Questions that arise include counting problems: "How many ways can these elements be combined?'' But there are other questions, such as whether a certain combination is possible, or what combination is the "best'' in some sense. We will see all of these, though counting plays a particularly large role.
Graph theory is concerned with various types of networks, or really models of networks called graphs. These are not the graphs of analytic geometry, but what are often described as "points connected by lines'', for example:
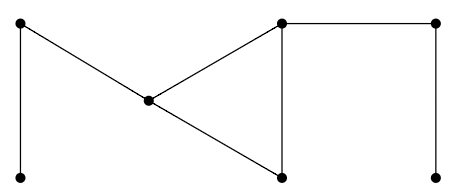
The preferred terminology is vertex for a point and edge for a line. The lines need not be straight lines, and in fact the actual definition of a graph is not a geometric definition. The figure above is simply a visualization of a graph; the graph is a more abstract object, consisting of seven vertices, which we might name \(\{v_1,\ldots,v_7\}\), and the collection of pairs of vertices that are connected; for a suitable assignment of names \(v_i\) to the points in the diagram, the edges could be represented as \(\{v_1,v_2\}\),\(\{v_2,v_3\}\),\(\{v_3,v_4\}\),\(\{v_3,v_5\}\),\(\{v_4,v_5\}\), \(\{v_5,v_6\}\),\(\{v_6,v_7\}\).


