1.2: Slope fields
- Page ID
- 336
The general first order equation we are studying looks like
\[ y' = f(x,y) \nonumber \]
In general, we cannot simply solve these kinds of equations explicitly. It would be nice if we could at least figure out the shape and behavior of the solutions, or if we could find approximate solutions. At this point it may be good to first try the Lab I and/or Project I from the IODE website.
Slope fields
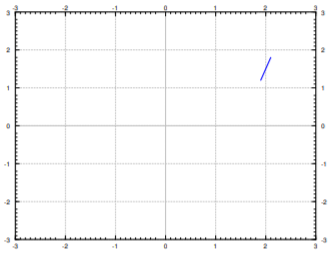
The equation \(y' = f(x,y)\) gives you a slope at each point in the \((x,y)\)-plane. And this is the slope a solution \(y(x)\) would have at \(x\) if its value was \(y\). In other words, \(f(x,y)\) is the slope of a solution whose graph runs through the point \((x,y)\). At a point \((x,y)\), we plot a short line with the slope \(f(x,y)\). For example, if \(f(x,y) = xy\), then at point \((2,1.5)\) we draw a short line of slope \(xy = 2 \times 1.5 = 3\). So, if \(y(x)\) is a solution and \(y(2) = 1.5\), then the equation mandates that \(y'(2) = 3\). See Figure \(\PageIndex{1}\).
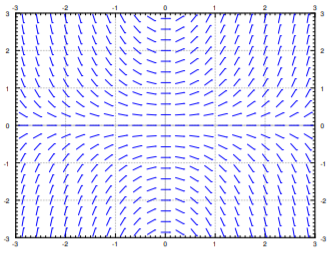
To get an idea of how solutions behave, we draw such lines at lots of points in the plane, not just the point \((2,1.5)\). We would ideally want to see the slope at every point, but that is just not possible. Usually we pick a grid of points fine enough so that it shows the behavior, but not too fine so that we can still recognize the individual lines. We call this picture the of the equation. See Figure \(\PageIndex{2}\) for the slope field of the equation \(y' = xy\). Usually in practice, one does not do this by hand, but has a computer do the drawing.
Suppose we are given a specific initial condition \(y(x_0) = y_0\). A solution, that is, the graph of the solution, would be a curve that follows the slopes we drew. For a few sample solutions, see Figure \(\PageIndex{3}\). It is easy to roughly sketch (or at least imagine) possible solutions in the slope field, just from looking at the slope field itself. You simply sketch a line that roughly fits the little line segments and goes through your initial condition.
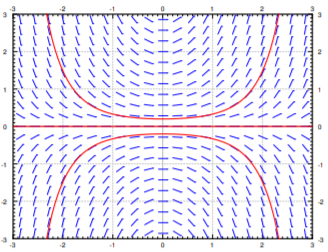
By looking at the slope field we get a lot of information about the behavior of solutions without having to solve the equation. For example, in Figure \(\PageIndex{3}\) we see what the solutions do when the initial conditions are \(y(0) > 0\), \(y(0) = 0\) and \(y(0) < 0\). A small change in the initial condition causes quite different behavior. We see this behavior just from the slope field and imagining what solutions ought to do.
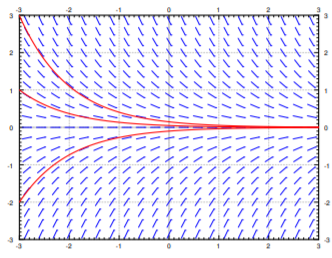
We see a different behavior for the equation \(y' = -y\). The slope field and a few solutions is in see Figure \(\PageIndex{4}\). If we think of moving from left to right (perhaps \(x\) is time and time is usually increasing), then we see that no matter what \(y(0)\) is, all solutions tend to zero as \(x\) tends to infinity. Again that behavior is clear from simply looking at the slope field itself.
Existence and uniqueness
We wish to ask two fundamental questions about the problem
\[ y' = f(x,y),\quad y(x_0) = y_0 \nonumber \]
- Does a solution exist?
- Is the solution unique (if it exists)?
What do you think is the answer? The answer seems to be yes to both does it not? Well, pretty much. But there are cases when the answer to either question can be no.
Since generally the equations we encounter in applications come from real life situations, it seems logical that a solution always exists. It also has to be unique if we believe our universe is deterministic. If the solution does not exist, or if it is not unique, we have probably not devised the correct model. Hence, it is good to know when things go wrong and why.
Attempt to solve
\[ y' = \dfrac {1}{x}, \quad y(0) = 0. \nonumber \]
Solution
Integrate to find the general solution \( y = \ln \left \vert x \right \vert + C\). Note that the solution does not exist at \( x = 0 \). See Figure \(\PageIndex{5}\) on the following page. The equation may have been written as the seemingly harmless \(xy'=1\).
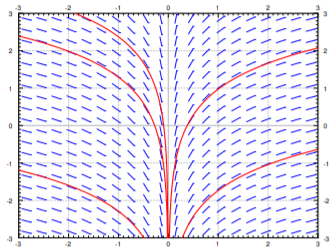
Solve:
\[ y' = 2 \sqrt {\left \vert y \right \vert}, \quad y(0) = 0 . \nonumber \]
Solution
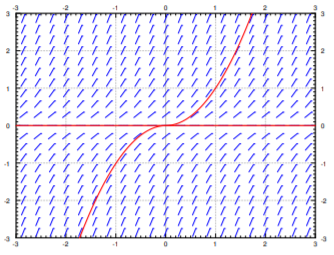
Note that \( y = 0 \) is a solution. But another solution is the function
\[ y(x) =\begin {cases} x^2 & {\rm{if~}} x \ge 0 \\ -x^2 & {\rm{if~}} x < 0 \end {cases} \nonumber \]
It is hard to tell by staring at the slope field that the solution is not unique. Is there any hope? Of course there is. We have the following theorem, known as Picard’s theorem.\(^{1}\)
Picard’s theorem on existence and uniqueness
If \( f(x,y) \) is continuous (as a function of two variables) and \(\dfrac{\partial f}{\partial y}\) exists and is continuous near some \( (x_0,y_0)\), then a solution to
\[y'=f(x,y),\quad y(x_{0})=y_{0} \nonumber \]
exists (at least for \(x\) in some small interval) and is unique.
Note that the problems \(y' = \dfrac{1}{x}\), \( y(0) = 0 \) and \( y' = 2 \sqrt {\left \vert y \right \vert}\), \( y(0) = 0 \) do not satisfy the hypothesis of the theorem. Even if we can use the theorem, we ought to be careful about this existence business. It is quite possible that the solution only exists for a short while.
For some constant \(A\), solve:
\[ y' = y^2\quad y(0) = A \nonumber \].
Solution
We know how to solve this equation. First assume that \( A \ne 0\), so \(y\) is not equal to zero at least for some \(x\) near 0. So \( x' = \dfrac{1}{y^2}\), so \(x = -\dfrac{1}{y} + C\), so \(y = \dfrac {1}{C - x}\). If \( y(0) = A \), then \( C = \dfrac{1}{A}\) so
\[ y = \dfrac {1}{\dfrac{1}{A} - x} \nonumber \]
If \( A = 0\), then \( y = 0 \) is a solution.
For example, when \(A = 1\) the solution “blows up” at \(x = 1\). Hence, the solution does not exist for all \(x\) even if the equation is nice everywhere. The equation \(y' = y^2\) certainly looks nice.
For most of this course we will be interested in equations where existence and uniqueness holds, and in fact holds “globally” unlike for the equation \(y' = y^2\).
Footnotes
[1] Named after the French mathematician Charles Émile Picard (1856 – 1941)


