11.3: Fourier Series II
- Page ID
- 9462
In this section we discuss Fourier expansions in terms of the eigenfunctions of Problems 1-4 for Section 11.1.
Fourier Cosine Series
From Exercise 11.1.20, the eigenfunctions
\[1,\, \cos{\pi x\over L}, \, \cos{2\pi x\over L},\dots, \, \cos{n\pi x\over L},\dots\nonumber \]
of the boundary value problem
\[\label{eq:11.3.1} y''+\lambda y=0,\quad y'(0)=0,\quad y'(L)=0\]
(Problem 2) are orthogonal on \([0,L]\). If \(f\) is integrable on \([0,L]\) then the Fourier expansion of \(f\) in terms of these functions is called the Fourier cosine series of \(f\) on \([0,L]\). This series is
\[a_0+\sum_{n=1}^\infty a_n\cos{n\pi x\over L},\nonumber \]
where
\[a_0={\int_0^Lf(x)\,dx\over\int_0^L\,dx}={1\over L}\int_0^Lf(x)\,dx\nonumber \]
and
\[a_n={\displaystyle\int_0^Lf(x)\cos{n\pi x\over L}\,dx\over\int_0^L \cos^2{n\pi x\over L}\,dx}={2\over L}\displaystyle\int_0^Lf(x)\cos{n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]
Comparing this definition with Theorem 11.2.6a shows that the Fourier cosine series of \(f\) on \([0,L]\) is the Fourier series of the function
\[f_{1}(x)=\left\{\begin{array}{cc}{f(-x),}&{-L<x<0,}\\{f(x),}&{}0\leq x\leq L\end{array} \right.\nonumber\]
obtained by extending \(f\) over \([-L,L]\) as an even function (Figure 11.3.1 ).
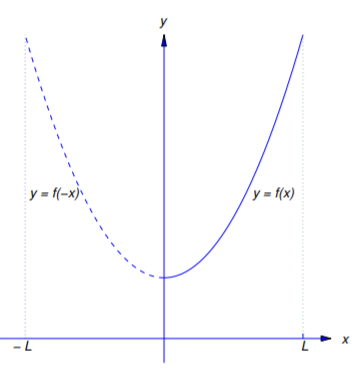
Applying Theorem 11.2.4 to \(f_1\) yields the next theorem.
If \(f\) is piecewise smooth on \([0,L]\), then the Fourier cosine series
\[C(x)=a_0+\sum_{n=1}^\infty a_n\cos{n\pi x\over L}\nonumber \]
of \(f\) on \([0,L]\), with
\[a_0={1\over L}\int_0^Lf(x)\,dx \quad \text{and} \quad a_n={2\over L}\int_0^Lf(x)\cos{n\pi x\over L}\,dx,\quad n=1,2,3,\dots,\nonumber \]
converges for all \(x\) in \([0,L];\) moreover,
\[C(x)=\left\{\begin{array}{cl}{f(0+),}&{\text{if }x=0}\\[5pt]{f(x),}&{\text{if } 0<x<L\text{ and }f \text{ is continuous at }x}\\[5pt]{\dfrac{f(x-)+f(x+)}{2},}&{\text{if }0<x<L\text{ and }f\text{ is discontinuous at }x}\\[5pt]{f(L-),}&{\text{if }x=L}\end{array} \right. \nonumber\]
Find the Fourier cosine series of \(f(x)=x\) on \([0,L]\).
The coefficients are
\[a_0={1\over L}\int_0^Lx\,dx=\left. {1\over L}{x^2\over2} \right|_{0}^{L}={L\over2}\nonumber \]
and, if \(n\ge1\)
\[\begin{aligned} a_n&={2\over L}\int_0^Lx\cos{n\pi x\over L}\,dx =\left. {2\over n\pi}\left[x\sin{n\pi x\over L}\right|_{0}^{L}- \int_0^L \sin{n\pi x\over L}\,dx\right]\\ &=-{2\over n\pi}\int_0^L \sin{n\pi x\over L}\,dx =\left.{2L\over n^2\pi^2}\cos{n\pi x\over L}\right|_{0}^{L} ={2L\over n^2\pi^2}[(-1)^n-1]\\ &= \left\{\begin{array}{cl} -{4L\over(2m-1)^2\pi^2},&{\text{if }n=2m-1},\\ 0,&{\text{if }n=2m}. \end{array}\right.\end{aligned}\nonumber \]
Therefore
\[C(x)=\frac{L}{2}-\frac{4L}{\pi ^{2}}\sum _{n=1}^{\infty}\frac{1}{(2n-1)^{2}}\cos\frac{(2n-1)\pi x}{L}\nonumber\]
Theorem 11.3.1 implies that
\[C(x)=x,\quad 0\le x\le L.\nonumber \]
Fourier Sine Series
From Exercise 11.1.19, the eigenfunctions
\[\sin{\pi x\over L}, \, \sin{2\pi x\over L},\dots, \, \sin{n\pi x\over L},\dots\nonumber \]
of the boundary value problem
\[y''+\lambda y=0,\quad y(0)=0,\quad y(L)=0\nonumber \]
(Problem 1) are orthogonal on \([0,L]\). If \(f\) is integrable on \([0,L]\) then the Fourier expansion of \(f\) in terms of these functions is called the Fourier sine series of \(f\) on \([0,L]\). This series is
\[\sum_{n=1}^\infty b_n\sin{n\pi x\over L},\nonumber \]
where
\[b_n={\displaystyle\int_0^Lf(x)\sin{n\pi x\over L}\,dx\over\displaystyle\int_0^L \sin^2{n\pi x\over L}\,dx}={2\over L}\int_0^Lf(x)\sin{n\pi x\over L}\,dx,\quad n=1,2,3,\dots.\nonumber \]
Comparing this definition with Theorem 11.2.6b shows that the Fourier sine series of \(f\) on \([0,L]\) is the Fourier series of the function
\[f_{2}(x)=\left\{\begin{array}{cc}{-f(-x),}&{-L<x<0}\\{f(x),}&{0\leq x\leq L,}\end{array} \right.\nonumber\]
obtained by extending \(f\) over \([-L,L]\) as an odd function (Figure 11.3.2 ).
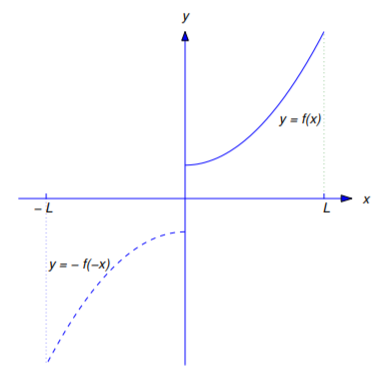
Applying Theorem 11.2.4 to \(f_2\) yields the next theorem.
If \(f\) is piecewise smooth on \([0,L]\), then the Fourier sine series
\[S(x)=\sum_{n=1}^\infty b_n\sin{n\pi x\over L}\nonumber \]
of \(f\) on \([0,L]\), with
\[b_n={2\over L}\int_0^Lf(x)\sin{n\pi x\over L}\,dx,\nonumber \]
converges for all \(x\) in \([0,L];\) moreover,
\[S(x)=\left\{\begin{array}{cl}{0}&{\text{if }x=0}\\[5pt]{f(x),}&{\text{if }0<x<L\text{ and }f\text{ is continuous at }x}\\[5pt]{\dfrac{f(x-)+f(x+)}{2},}&{\text{if }0<x<L\text{ and }f\text{ is discontinuous at }x}\\[5pt]{0,}&{\text{if }x=L}\end{array} \right.\nonumber\]
Find the Fourier sine series of \(f(x)=x\) on \([0,L]\).
Solution
The coefficients are
\[\begin{aligned} b_n&={2\over L}\int_0^Lx\sin{n\pi x\over L}\,dx =\left.-{2\over n\pi}\left[x\cos{n\pi x\over L}\right|_{0}^{L}- \int_0^L \cos{n\pi x\over L}\,dx\right]\\ &=\left. (-1)^{n+1}{2L\over n\pi}+{2L\over n^2\pi^2}\sin{n\pi x\over L}\right|_{0}^{L} =(-1)^{n+1}{2L\over n\pi}.\end{aligned}\nonumber \]
Therefore
\[S(x)=-{2L\over\pi}\sum_{n=1}^\infty{(-1)^n\over n} \sin{n\pi x\over L}.\nonumber \]
Theorem 11.3.2 implies that
\[S(x)= \left\{\begin{array}{cl} x,&0\le x< L,\\0,& x=L. \end{array}\right.\nonumber \]
Mixed Fourier Cosine Series
From Exercise 11.1.22, the eigenfunctions
\[\cos{\pi x\over 2L}, \, \cos{3\pi x\over 2L},\dots, \, \cos{(2n-1)\pi x\over 2L},\dots\nonumber \]
of the boundary value problem
\[\label{eq:11.3.2} y''+\lambda y=0,\quad y'(0)=0,\quad y(L)=0\]
(Problem 4) are orthogonal on \([0,L]\). If \(f\) is integrable on \([0,L]\) then the Fourier expansion of \(f\) in terms of these functions is
\[\sum_{n=1}^\infty c_n\cos{(2n-1)\pi x\over2L},\nonumber \]
where
\[c_n={\displaystyle\int_0^Lf(x)\cos{(2n-1)\pi x\over2L}\,dx\over\displaystyle\int_0^L \cos^2{(2n-1)\pi x\over L}\,dx}={2\over L}\int_0^Lf(x)\cos{(2n-1)\pi x\over2L}\,dx.\nonumber \]
We’ll call this expansion the mixed Fourier cosine series of \(f\) on \([0,L]\), because the boundary conditions of ( Equation \ref{eq:11.3.2}) are “mixed” in that they require \(y\) to be zero at one boundary point and \(y'\) to be zero at the other. By contrast, the “ordinary” Fourier cosine series is associated with ( Equation \ref{eq:11.3.1}), where the boundary conditions require that \(y'\) be zero at both endpoints.
It can be shown (Exercise 11.3.57) that the mixed Fourier cosine series of \(f\) on \([0,L]\) is simply the restriction to \([0,L]\) of the Fourier cosine series of
\[f_3(x)= \left\{\begin{array}{cl} f(x),&0\le x\le L,\\-f(2L-x),&L< x\le 2L \end{array}\right.\nonumber \]
on \([0,2L]\) (Figure 11.3.3 ).
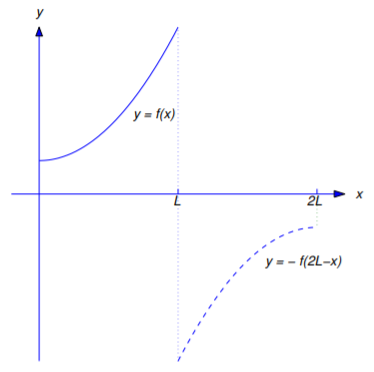
Applying Theorem 11.3.1 with \(f\) replaced by \(f_3\) and \(L\) replaced by \(2L\) yields the next theorem.
If \(f\) is piecewise smooth on \([0,L]\), then the mixed Fourier cosine series
\[C_M(x)=\sum_{n=1}^\infty c_n\cos{(2n-1)\pi x\over2L}\nonumber \]
of \(f\) on \([0,L]\), with
\[c_n={2\over L}\int_0^Lf(x)\cos{(2n-1)\pi x\over2L}\,dx,\nonumber \]
converges for all \(x\) in \([0,L];\) moreover,
\[C_{M}(x)=\left\{\begin{array}{cl}{f(0+),}&{\text{if }x=0}\\[5pt]{f(x),}&{\text{if }0<x<L\text{ and }f\text{ is continuous at }x}\\[5pt]{\dfrac{f(x-)+f(x+)}{2},}&{\text{if }0<x<L\text{ and }f\text{ is discontinuous at }x}\\[5pt]{0,}&{\text{if }x=L}\end{array} \right.\nonumber\]
Find the mixed Fourier cosine series of \(f(x)=x-L\) on \([0,L]\).
Solution
The coefficients are
\[\begin{aligned} c_n&={2\over L}\int_0^L(x-L)\cos{(2n-1)\pi x\over2L}\,dx\\ &=\left.{4\over(2n-1)\pi}\left[(x-L)\sin{(2n-1)\pi x\over2L}\right|_{0}^{L}-\int_0^L \sin{(2n-1)\pi x\over2L}\,dx\right]\\ &=\left.{8L\over(2n-1)^2\pi^2} \cos{(2n-1)\pi x\over2L}\right|_{0}^{L} =-{8L\over(2n-1)^2\pi^2}.\end{aligned}\nonumber \]
Therefore
\[C_M(x)=-{8L\over\pi^2}\sum_{n=1}^\infty{1\over(2n-1)^2} \cos{(2n-1)\pi x\over2L}.\nonumber \]
Theorem 11.3.3 implies that
\[C_M(x)= x-L,\quad 0\le x\le L.\nonumber \]
Mixed Fourier Sine Series
From Exercise 11.1.21, the eigenfunctions
\[\sin{\pi x\over 2L}, \, \sin{3\pi x\over 2L},\dots, \, \sin{(2n-1)\pi x\over 2L},\dots\nonumber \]
of the boundary value problem
\[y''+\lambda y=0,\quad y(0)=0,\quad y'(L)=0\nonumber \]
(Problem 3) are orthogonal on \([0,L]\). If \(f\) is integrable on \([0,L]\), then the Fourier expansion of \(f\) in terms of these functions is
\[\sum_{n=1}^\infty d_n\sin{(2n-1)\pi x\over2L},\nonumber \]
where
\[d_n={\displaystyle\int_0^Lf(x)\sin{(2n-1)\pi x\over2L}\,dx\over\displaystyle\int_0^L \sin^2{(2n-1)\pi x\over2L}\,dx}={2\over L}\int_0^Lf(x)\sin{(2n-1)\pi x\over2L}\,dx.\nonumber \]
We’ll call this expansion the mixed Fourier sine series of \(f\) on \([0,L]\).
It can be shown (Exercise 11.3.58) that the mixed Fourier sine series of \(f\) on \([0,L]\) is simply the restriction to \([0,L]\) of the Fourier sine series of
\[f_4(x)= \left\{\begin{array}{cl} f(x),&0\le x\le L,\\f(2L-x),&L< x\le 2L, \end{array}\right.\nonumber \]
on \([0,2L]\) (Figure 11.3.4 ).
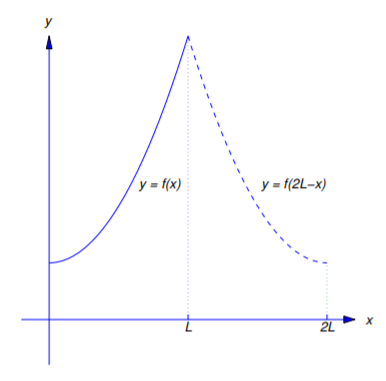
Applying Theorem 11.3.2 with \(f\) replaced by \(f_4\) and \(L\) replaced by \(2L\) yields the next theorem.
If \(f\) is piecewise smooth on \([0,L]\), then the mixed Fourier sine series
\[S_M(x)=\sum_{n=1}^\infty d_n\sin{(2n-1)\pi x\over2L}\nonumber \]
of \(f\) on \([0,L]\), with
\[d_n={2\over L}\int_0^Lf(x)\sin{(2n-1)\pi x\over2L}\,dx,\nonumber \]
converges for all \(x\) in \([0,L];\) moreover,
\[S{M}(x)=\left\{\begin{array}{cl}{0,}&{\text{if }x=0}\\[5pt]{f(x),}&{\text{if }0<x<L\text{ and }f\text{ is continuous at }x}\\[5pt]{\dfrac{f(x-)+f(x+)}{2},}&{\text{if }0<x<L\text{ and }f\text{ is discontinuous at }x}\\[5pt]{f(L-),}&{\text{if }x=L}\end{array} \right.\nonumber\]
Find the mixed Fourier sine series of \(f(x)=x\) on \([0,L]\).
Solution
The coefficients are
\[\begin{aligned} d_n&={2\over L}\int_0^Lx\sin{(2n-1)\pi x\over2L}\,dx\\ &=\left.-{4\over(2n-1)\pi}\left[x\cos{(2n-1)\pi x\over2L}\right|_{0}^{L}- \int_0^L \cos{(2n-1)\pi x\over2L}\,dx\right]\\ &={4\over(2n-1)\pi} \int_0^L \cos{(2n-1)\pi x\over2L}\,dx\\ &=\left.{8L\over(2n-1)^2\pi^2}\sin{(2n-1)\pi x\over2L}\right|_{0}^{L}=(-1)^{n+1}{8L\over(2n-1)^2\pi^2}.\end{aligned}\nonumber \]
Therefore
\[S_M(x)=-{8L\over\pi^2}\sum_{n=1}^\infty{(-1)^n\over(2n-1)^2} \sin{(2n-1)\pi x\over2L}.\nonumber \]
Theorem 11.3.4 implies that
\[S_M(x)=x,\quad 0\le x\le L.\nonumber \]
A Useful Observation
In applications involving expansions in terms of the eigenfunctions of Problems 1-4, the functions being expanded are often polynomials that satisfy the boundary conditions of the problem under consideration. In this case the next theorem presents an efficient way to obtain the coefficients in the expansion.
- If \(f'(0)=f'(L)=0\), \(f''\) is continuous\(,\) and \(f'''\) is piecewise continuous on \([0,L],\) then \[\label{eq:11.3.3} f(x)=a_0+\sum_{n=1}^\infty a_n\cos{n\pi x\over L}, \quad 0\le x\le L,\] with \[\label{eq:11.3.4} a_0={1\over L}\int_0^L f(x)\,dx \quad \text{and} \quad a_n= {2L^2\over n^3\pi^3}\int_0^L f'''(x)\sin{n\pi x\over L}\,dx, \quad n\ge1.\] Now suppose \(f'\) is continuous and \(f''\) is piecewise continuous on \([0,L].\)
- If \(f(0)=f(L)=0\), then \[f(x)=\sum_{n=1}^\infty b_n\sin{n\pi x\over L}, \quad 0\le x\le L,\nonumber \] with \[\label{eq:11.3.5} b_n=-{2L\over n^2\pi^2}\int_0^L f''(x)\sin{n\pi x\over L}\,dx.\]
- If \(f'(0)=f(L)=0\), then \[f(x)= \sum_{n=1}^\infty c_n\cos{(2n-1)\pi x\over2L}, \quad 0\le x\le L,\nonumber \] with \[\label{eq:11.3.6} c_n=-{8L\over(2n-1)^2\pi^2}\int_0^L f''(x)\cos{(2n-1)\pi x\over2L} \,dx.\]
- If \(f(0)=f'(L)=0\), then \[f(x)= \sum_{n=1}^\infty d_n\sin{(2n-1)\pi x\over2L}, \quad 0\le x\le L,\nonumber \] with \[\label{eq:11.3.7} d_n=-{8L\over(2n-1)^2\pi^2}\int_0^L f''(x)\sin{(2n-1)\pi x\over2L} \,dx.\]
- Proof
-
We'll prove (a) and leave the rest to you (Exercises 11.3.35, 11.3.42, and 11.3.50). Since \(f\) is continuous on \([0,L]\), Theorem 11.3.1 implies ( Equation \ref{eq:11.3.3}) with \(a_0\), \(a_1\), \(a_2\),... as defined in Theorem 11.3.1 . We already know that \(a_0\) is as in ( Equation \ref{eq:11.3.4}). If \(n\ge1\), integrating twice by parts yields
\[\begin{aligned} a_n&= {2\over L}\int_0^L f(x)\cos{n\pi x\over L}\,dx\\ &=\left.{2\over n\pi}\left[f(x)\sin{n\pi x\over L}\right|_{0}^{L} -\int_0^Lf'(x)\sin{n\pi x\over L}\,dx\right]\\ &=-{2\over n\pi} \int_0^Lf'(x)\sin{n\pi x\over L}\,dx \mbox{ (since $\sin0=\sin n\pi=0$)}\\ &=\left.{2L\over n^2\pi^2}\left[f'(x)\cos{n\pi x\over L}\right|_{0}^{L} -\int_0^Lf''(x)\cos{n\pi x\over L}\right]\,dx\\ &= -{2L\over n^2\pi^2}\int_0^Lf''(x)\cos{n\pi x\over L}\,dx \mbox{ (since $f'(0)=f'(L)=0$)}\\ &=\left.-{2L^2\over n^3\pi^3}\left[f''(x)\sin{n\pi x\over L}\right|_{0}^{L} -\int_0^Lf'''(x)\sin{n\pi x\over L}\,dx\right]\\ &= {2L^2\over n^3\pi^3}\int_0^Lf'''(x)\sin{n\pi x\over L}\,dx \mbox{ (since $\sin0=\sin n\pi=0$).}\end{aligned}\nonumber \]
(By an argument similar to one used in the proof of Theorem 8.3.1, the last integration by parts is legitimate in the case where \(f'''\) is undefined at finitely many points in \([0,L]\), so long as it is piecewise continuous on \([0,L]\).) This completes the proof.
Find the Fourier cosine expansion of \(f(x)=x^2(3L-2x)\) on \([0,L]\).
Solution
Here
\[a_0={1\over L}\int_0^L(3Lx^2-2x^3)\,dx=\left.{1\over L}\left(Lx^3-{x^4\over2} \right)\right|_{0}^{L}={L^3\over2}\nonumber \]
and
\[a_n={2\over L}\int_0^L(3Lx^2-2x^3)\cos{n\pi x\over L}\,dx,\quad n\ge1.\nonumber \]
Evaluating this integral directly is laborious. However, since \(f'(x)=6Lx-6x^2\), we see that \(f'(0)=f'(L)=0\). Since \(f'''(x)=-12\), we see from ( Equation \ref{eq:11.3.4}) that if \(n\ge1\) then
\[\begin{aligned} a_n&=-{24L^2\over n^3\pi^3}\int_0^L\sin{n\pi x\over L}\,dx =\left.{24L^3\over n^4\pi^4}\cos{n\pi x\over L}\right|_{0}^{L}={24L^3\over n^4\pi^4}[(-1)^n-1]\\ &= \left\{\begin{array}{cl} -{48L^3\over(2m-1)^4\pi^4},&\mbox{if $n=2m-1$},\\ 0,&\mbox{if $n=2m$.} \end{array}\right.\end{aligned}\nonumber \]
Therefore
\[C(x)={L^3\over2}-{48L^3\over\pi^4}\sum_{n=1}^\infty{1\over (2n-1)^4}\cos{(2n-1)\pi x\over L}.\nonumber \]
Find the Fourier sine expansion of \(f(x)=x(x^2-3Lx+2L^2)\) on \([0,L]\).
Solution
Since \(f(0)=f(L)=0\) and \(f''(x)=6(x-L)\), we see from ( Equation \ref{eq:11.3.5}) that
\[\begin{aligned} b_n&=- {12L\over n^2\pi^2}\int_0^L(x-L)\sin{n\pi x\over L}\,dx\\ &=\left.{12L^2\over n^3\pi^3}\left[(x-L)\cos{n\pi x\over L}\right|_{0}^{L} -\int_0^L\cos{n\pi x\over L}\,dx\right]\\ &=\left.{12L^2\over n^3\pi^3}\left[L-\frac{L}{n\pi}\sin\frac{n\pi x}{L}\right|_{0}^{L}\right] ={12L^3\over n^3\pi^3}.\end{aligned}\nonumber \]
Therefore
\[S(x)=\frac{12L^{3}}{\pi ^{3}}\sum_{n=1}^{\infty}\frac{1}{n^{3}}\sin\frac{n\pi x}{L}\nonumber\]
Find the mixed Fourier cosine expansion of \(f(x)=3x^3-4Lx^2+L^3\) on \([0,L]\).
Solution
Since \(f'(0)=f(L)=0\) and \(f''(x)=2(9x-4L)\), we see from ( Equation \ref{eq:11.3.6}) that
\[\begin{aligned} c_n&= -{16L\over(2n-1)^2\pi^2} \int_0^L(9x-4L)\cos{(2n-1)\pi x\over2L}\,dx\\ &=\left.-{32L^2\over(2n-1)^3\pi^3}\left[(9x-4L)\sin{(2n-1)\pi x\over2L} \right|_{0}^{L}-9\int_0^L\sin{(2n-1)\pi x\over2L}\right]\,dx\\ &=\left.-{32L^2\over(2n-1)^3\pi^3} \left[(-1)^{n+1}5L+{18L\over(2n-1)\pi}\cos{(2n-1)\pi x\over2L} \right|_{0}^{L}\right] \\ &={32L^3\over(2n-1)^3\pi^3} \left[(-1)^n5+{18\over(2n-1)\pi}\right].\end{aligned}\nonumber \]
Therefore
\[C_{M}(x)=\frac{32L^{3}}{\pi ^{3}}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^{3}}\left[(-1)^{n}5+\frac{18}{(2n-1)\pi } \right]\cos\frac{(2n-1)\pi x}{2L}\nonumber\]
Find the mixed Fourier sine expansion of
\[f(x)=x(2x^2-9Lx+12L^2)\nonumber \]
on \([0,L]\).
Solution
Since \(f(0)=f'(L)=0\), and \(f''(x)=6(2x-3L)\), we see from ( Equation \ref{eq:11.3.7}) that
\[\begin{aligned} d_{n}&=-\frac{48L}{(2n-1)^{2}\pi ^{2}}\int_{0}^{L}(2x-3L)\sin\frac{(2n-1)\pi x}{2L}dx \\ &=\left.\frac{96L^{2}}{(2n-1)^{3}\pi ^{3}}\left[(2x-3L)\cos\frac{(2n-1)\pi x}{2L}\right|_{0}^{L} - 2\int_{0}^{L}\cos\frac{(2n-1)\pi x}{2L}dx \right] \\ &=\left. \frac{96L^{2}}{(2n-1)^{3}\pi ^{3}}\left[3L-\frac{4L}{(2n-1)\pi }\sin\frac{(2n-1)\pi x}{2L}\right|_{0}^{L} \right] \\&=\frac{96L^{3}}{(2n-1)^{3}\pi ^{3}}\left[3+(-1)^{n}\frac{4}{(2n-1)\pi } \right] \end{aligned}\nonumber\]
Therefore
\[S_{M}(x)=\frac{96L^{3}}{\pi ^{3}}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^{3}}\left[3+(-1)^{n}\frac{4}{(2n-1)\pi } \right]\sin\frac{(2n-1)\pi x}{2L}\nonumber\]


