12.3: Laplace's Equation in Rectangular Coordinates
- Page ID
- 9469
The temperature \(u=u(x,y,t)\) in a two-dimensional plate satisfies the two-dimensional heat equation
\[\label{eq:12.3.1} u_t=a^2(u_{xx}+u_{yy}),\]
where \((x,y)\) varies over the interior of the plate and \(t>0\). To find a solution of Equation \ref{eq:12.3.1}, it is necessary to specify the initial temperature \(u(x,y,0)\) and conditions that must be satisfied on the boundary. However, as \(t\to\infty\), the influence of the initial condition decays, so
\[\lim_{t\to\infty}u_t(x,y,t)=0 \nonumber \]
and the temperature approaches a steady state distribution \(u=u(x,y)\) that satisfies
\[\label{eq:12.3.2} u_{xx}+u_{yy}=0.\]
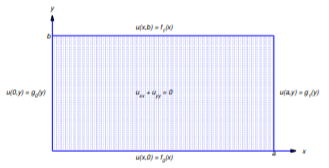
This is Laplace’s equation. This equation also arises in applications to fluid mechanics and potential theory; in fact, it is also called the potential equation. We seek solutions of Equation \ref{eq:12.3.2} in a region \(R\) that satisfy specified conditions – called boundary conditions – on the boundary of \(R\). For example, we may require \(u\) to assume prescribed values on the boundary. This is called a Dirichlet condition, and the problem is called a Dirichlet problem. Or, we may require the normal derivative of \(u\) at each point \((x,y)\) on the boundary to assume prescribed values. This is called a Neumann condition, and the problem is called a Neumann problem. In some problems we impose Dirichlet conditions on part of the boundary and Neumann conditions on the rest. Then we say that the boundary conditions and the problem are mixed.
Solving boundary value problems for Equation \ref{eq:12.3.2} over general regions is beyond the scope of this book, so we consider only very simple regions. We begin by considering the rectangular region shown in Figure 12.3.1 .

The possible boundary conditions for this region can be written as
\[\begin{array}{lcllll} (1-\alpha)u(x,0)&+&\alpha u_y(x,0)&=&f_0(x), &0\le x\le a,\\[4pt] (1-\beta) u(x,b)&+&\beta u_y(x,b)&=&f_1(x), &0\le x\le a,\\[4pt] (1-\gamma) u(0,y)&+&\gamma u_x(0,y)&=&g_0(y), &0\le y\le b,\\[4pt] (1-\delta) u(a,y)&+&\delta u_x(a,y)&=&g_1(y), &0\le y\le b, \end{array}\nonumber\]
where \(\alpha\), \(\beta\), \(\gamma\), and \(\delta\) can each be either \(0\) or \(1\); thus, there are 16 possibilities. Let BVP\((\alpha,\beta,\gamma,\delta)(f_0,f_1,g_0,g_1)\) denote the problem of finding a solution of Equation \ref{eq:12.3.2} that satisfies these conditions. This is a Dirichlet problem if
\[\alpha=\beta=\gamma=\delta=0\nonumber\]
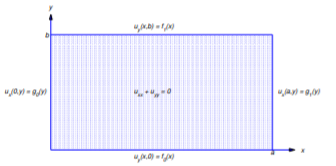
(Figure 12.3.2 ), or a Neumann problem if
\[\alpha=\beta=\gamma=\delta=1\nonumber\]
(Figure 12.3.3 ). The other 14 problems are mixed.
For given \((\alpha,\beta,\gamma,\delta)\), the sum of solutions of
\[\mbox{BVP}(\alpha,\beta,\gamma,\delta)(f_0,0,0,0),\quad \mbox{BVP}(\alpha,\beta,\gamma,\delta)(0,f_1,0,0),\nonumber\]
\[\mbox{BVP}(\alpha,\beta,\gamma,\delta)(0,0,g_0,0), \quad \text{and} \quad \mbox{BVP}(\alpha,\beta,\gamma,\delta)(0,0,0,g_1)\nonumber\]
is a solution of
\[\mbox{BVP}(\alpha,\beta,\gamma,\delta)(f_0,f_1,g_0,g_1).\nonumber\]
Therefore we concentrate on problems where only one of the functions \(f_0\), \(f_1\), \(g_0\), \(g_2\) isn’t identically zero. There are 64 (count them!) problems of this form. Each has homogeneous boundary conditions on three sides of the rectangle, and a nonhomogeneous boundary condition on the fourth. We use separation of variables to find infinitely many functions that satisfy Laplace’s equation and the three homogeneous boundary conditions in the open rectangle. We then use these solutions as building blocks to construct a formal solution of Laplace’s equation that also satisfies the nonhomogeneous boundary condition. Since it is not feasible to consider all 64 cases, we’ll restrict our attention in the text to just four. Others are discussed in the exercises.
If \(v(x,y)=X(x)Y(y)\) then
\[v_{xx}+v_{yy}=X''Y+XY''=0\nonumber\]
for all \((x,y)\) if and only if
\[{X''\over X}=-{Y''\over Y}=k\nonumber\]
for all \((x,y)\), where \(k\) is a separation constant. This equation is equivalent to
\[\label{eq:12.3.3} X''-kX=0,\quad Y''+kY=0.\]
From here, the strategy depends upon the boundary conditions. We illustrate this by examples.
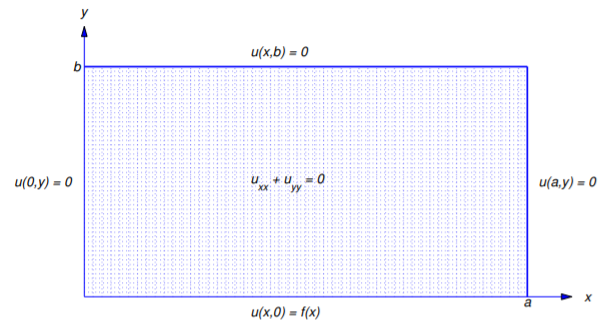
Define the formal solution of
\[\label{eq:12.3.4} \begin{array}{ccc} {u_{xx}+u_{yy}=0,}&{0<x<a,}&{0<y<b,}\\{u(x,0)=f(x),}&{u(x,b)=0,}&{0\leq x\leq a,}\\{u(0,y)=0,}&{u(a,y)=0,}&{0\leq y\leq b}\end{array}\]
(Figure 12.3.4 ).
Solution:
The boundary conditions in Equation \ref{eq:12.3.4} require products \(v(x,y)=X(x)Y(y)\) such that \(X(0)=X(a)=Y(b)=0\); hence, we let \(k=-\lambda\) in Equation \ref{eq:12.3.3}. Thus, \(X\) and \(Y\) must satisfy
\[\label{eq:12.3.5} X''+\lambda X=0,\quad X(0)=0,\quad X(a)=0\]
and
\[\label{eq:12.3.6} Y''-\lambda Y=0,\quad Y(b)=0.\]
From Theorem 11.1.2, the eigenvalues of Equation \ref{eq:12.3.5} are \(\lambda_n=n^2\pi^2/a^2\), with associated eigenfunctions
\[X_n=\sin{n\pi x\over a}, \quad n=1,2,3,\dots.\nonumber\]
Substituting \(\lambda=n^2\pi^2/a^2\) into Equation \ref{eq:12.3.6} yields
\[Y''-(n^2\pi^2/a^2)Y=0,\quad Y(b)=0,\nonumber\]
so we could take
\[\label{eq:12.3.7} Y_n=\sinh{n\pi(b-y)\over a};\]
however, because of the nonhomogeneous Dirichlet condition at \(y=0\), it is better to require that \(Y_n(0)=1\), which can be achieved by dividing the right side of Equation \ref{eq:12.3.7} by its value at \(y=0\); thus, we take
\[Y_n={\sinh n\pi(b-y)/a\over\sinh n\pi b/a}.\nonumber\]
Then
\[v_n(x,y)=X_n(x)Y_n(y)={\sinh n\pi(b-y)/a\over\sinh n\pi b/a}\sin{n\pi x\over a},\nonumber\]
so \(v_n(x,0)=\sin n\pi x/a\) and \(v_n\) satisfies Equation \ref{eq:12.3.4} with \(f(x)=\sin n\pi x/a\). More generally, if \(\alpha_1\), …, \(\alpha_m\) are arbitrary constants then
\[u_m(x,y)=\sum_{n=1}^m\alpha_n {\sinh n\pi(b-y)/a\over\sinh n\pi b/a} \sin{n\pi x\over a}\nonumber\]
satisfies Equation \ref{eq:12.3.4} with
\[f(x)=\sum_{n=1}^m\alpha_n\sin{n\pi x\over L}.\nonumber\]
Therefore, if \(f\) is an arbitrary piecewise smooth function on \([0,a]\), we define the formal solution of Equation \ref{eq:12.3.4} to be
\[\label{eq:12.3.8} u(x,y)=\sum_{n=1}^\infty \alpha_n {\sinh n\pi(b-y)/a\over\sinh n\pi b/a} \sin{n\pi x\over a},\]
where
\[S(x)=\sum_{n=1}^\infty \alpha_n\sin{n\pi x\over a}\nonumber\]
is the Fourier sine series of \(f\) on \([0,a]\); that is,
\[\alpha_n={2\over a}\int_0^af(x)\sin{n\pi x\over a}\,dx,\quad n=1,2,3,\dots.\nonumber\]
If \(y<b\) then
\[\label{eq:12.3.9} {\sinh n\pi(b-y)/a\over\sinh n\pi b/a}\approx e^{-n\pi y/a}\]
for large \(n\), so the series in Equation \ref{eq:12.3.8} converges if \(0< y < b\); moreover, since also
\[{\cosh n\pi(b-y)/a\over\sinh n\pi b/a}\approx e^{-n\pi y/a}\nonumber\]
for large \(n\), Theorem 12.1.2 applied twice with \(z=x\) and twice with \(z=t\), shows that \(u_{xx}\) and \(u_{yy}\) can be obtained by differentiating \(u\) term by term if \(0<y<b\)
Solve Equation \ref{eq:12.3.4} with \(f(x)=x(x^2-3ax+2a^2)\).
Solution
From Example 11.3.6,
\[S(x)={12a^3\over\pi^3}\sum_{n=1}^\infty{1\over n^3}\sin{n\pi x\over a}.\nonumber\]
Therefore
\[\label{eq:12.3.10} u(x,y)={12a^3\over\pi^3}\sum_{n=1}^\infty{\sinh n\pi(b-y)/a\over n^3\sinh n\pi b/a} \sin{n\pi x\over a}.\]
To compute approximate values of \(u(x,y)\), we must use partial sums of the form
\[u_m(x,y)={12a^3\over\pi^3}\sum_{n=1}^m{\sinh n\pi(b-y)/a\over n^3\sinh n\pi b/a} \sin{n\pi x\over a}.\nonumber\]
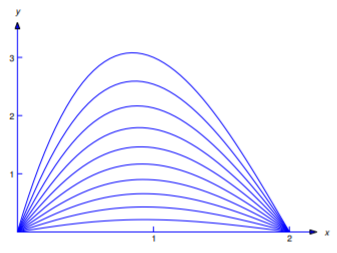
Because of Equation \ref{eq:12.3.9}, small values of \(m\) provide sufficient accuracy for most applications if \(0<y<b\). Moreover, the \(n^{3}\) in the denominator in \ref{eq:12.3.10} ensures that this is also true for \(y = 0\). For graphing purposes, we chose \(a = 2, b = 1\), and \(m = 10\). Figure 12.3.5 shows the surface
\[u=u(x,y),\quad 0\le x\le 2,\quad 0\le y\le1,\nonumber\]
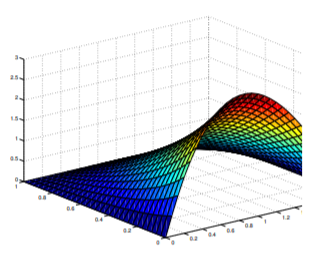
while Figure 12.3.6 shows the curves
\[u=u(x,0.1k),\quad 0\le x\le2,\quad k=0,1,\dots,10.\nonumber\]
Define the formal solution of
\[\label{eq:12.3.11} \begin{array}{ccc}{u_{xx}+u_{yy}=0,}&{0<x<a,}&{0<y<b,}\\{u(x,0)=0,}&{u_{y}(x,b)=f(x),}&{0\leq x\leq a,}\\{u_{x}(0,y)=0,}&{u_{x}(a,y)=0,}&{0\leq y\leq b}\end{array}\]
(Figure 12.3.7 ).
Solution
The boundary conditions in Equation \ref{eq:12.3.11} require products \(v(x,y)=X(x)Y(y)\) such that \(X'(0)=X'(a)=Y(0)=0\); hence, we let \(k=-\lambda\) in Equation \ref{eq:12.3.3}. Thus, \(X\) and \(Y\) must satisfy
\[\label{eq:12.3.12} X''+\lambda X=0,\quad X'(0)=0,\quad X'(a)=0\]
and
\[\label{eq:12.3.13} Y''-\lambda Y=0,\quad Y(0)=0.\]
From Theorem 11.1.3, the eigenvalues of Equation \ref{eq:12.3.12} are \(\lambda=0\), with associated eigenfunction \(X_0=1\), and \(\lambda_n=n^2\pi^2/a^2\), with associated eigenfunctions
\[X_n=\cos{n\pi x\over a}, \quad n=1,2,3,\dots.\nonumber\]
Since \(Y_0=y\) satisfies Equation \ref{eq:12.3.13} with \(\lambda=0\), we take \(v_0(x,y)=X_0(x)Y_0(y)= y\). Substituting \(\lambda=n^2\pi^2/a^2\) into Equation \ref{eq:12.3.13} yields
\[Y''-(n^2\pi^2/a^2)Y=0,\quad Y(0)=0,\nonumber\]
so we could take
\[\label{eq:12.3.14} Y_n=\sinh{n\pi y\over a}.\]
However, because of the nonhomogeneous Neumann condition at \(y=b\), it is better to require that \(Y_n'(b)=1\), which can be achieved by dividing the right side of Equation \ref{eq:12.3.14} by the value of its derivative at \(y=b\); thus,
\[Y_n={a\sinh n\pi y/a\over n\pi\cosh n\pi b/a}.\nonumber\]
Then
\[v_n(x,y)=X_n(x)Y_n(y)= {a\sinh n\pi y/a\over n\pi\cosh n\pi b/a}\cos{n\pi x\over a},\nonumber\]
so
\[{\partial v_n\over \partial y}(x,b)=\cos{n\pi x\over a}.\nonumber\]
Therefore \(v_n\) satisfies Equation \ref{eq:12.3.11} with \(f(x)=\cos n\pi x/a\). More generally, if \(\alpha_0\), …, \(\alpha_m\) are arbitrary constants then
\[u_m(x,y)=\alpha_0y+{a\over\pi}\sum_{n=1}^m\alpha_n {\sinh n\pi y/a\over n\cosh n\pi b/a} \cos{n\pi x\over a}\nonumber\]
satisfies Equation \ref{eq:12.3.11} with
\[f(x)=\alpha_0+\sum_{n=1}^m\alpha_n\cos{n\pi x\over L}.\nonumber\]
Therefore, if \(f\) is an arbitrary piecewise smooth function on \([0,a]\) we define the formal solution of Equation \ref{eq:12.3.11} to be
\[u(x,y)=\alpha_0y+{a\over\pi}\sum_{n=1}^\infty \alpha_n {\sinh n\pi y/a\over n\cosh n\pi b/a} \cos{n\pi x\over a},\nonumber\]
where
\[C(x)=\alpha_0+\sum_{n=1}^\infty \alpha_n\cos{n\pi x\over a}\nonumber\]
is the Fourier cosine series of \(f\) on \([0,a]\); that is,
\[\alpha_0={1\over a}\int_0^af(x)\,dx \quad \text{and} \quad \alpha_n={2\over a}\int_0^af(x)\cos{n\pi x\over a}\,dx,\quad n=1,2,3,\dots.\nonumber\]
Solve Equation \ref{eq:12.3.11} with \(f(x)=x\).
Solution
From Example 11.3.1,
\[C(x)=\frac{a}{2}-\frac{4a}{\pi ^{2}}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^{2}}\cos\frac{(2n-1)\pi x}{a}\nonumber\]
Therefore
\[\label{eq:12.3.15} u(x,y)=\frac{ay}{2}-\frac{4a^{2}}{\pi ^{3}}\sum_{n=1}^{\infty}\frac{\sinh (2n-1)\pi y/a}{(2n-1)^{3}\cosh (2n-1)\pi b/a}\cos\frac{(2n-1)\pi x}{a}\]
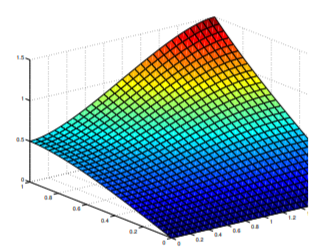
For graphing purposes, we chose \(a=2\), \(b=1\), and retained the terms through \(n=10\) in Equation \ref{eq:12.3.15}. Figure 12.3.8 shows the surface
\[u=u(x,y),\quad 0\le x\le 2,\quad 0\le y\le1,\nonumber\]
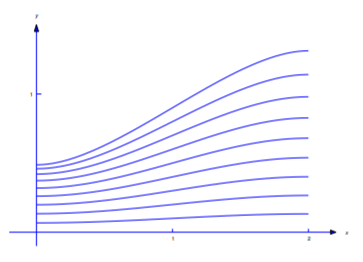
while Figure 12.3.9 shows the curves
\[u=u(x,.1k),\quad 0\le x\le2,\quad k=0,1,\dots,10.\nonumber\]
Define the formal solution of
\[\label{eq:12.3.16} \begin{array}{ccc}{u_{xx}+u_{yy}=0,}&{0<x<a,}&{0<y<b,}\\{u(x,0)=0,}&{u_{y}(x,b)=0,}&{0\leq x\leq a,}\\{u(0,y)=g(y),}&{u_{x}(a,y)=0,}&{0\leq y\leq b}\end{array}\]
(Figure 12.3.10 ).
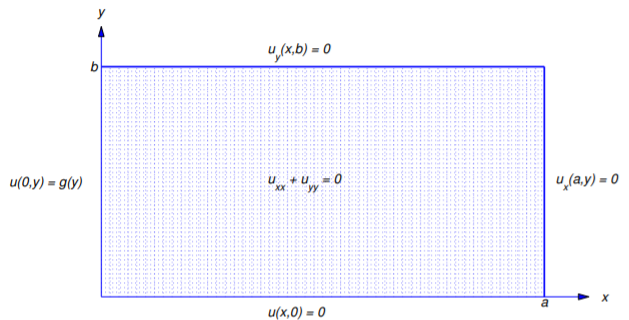
Solution
The boundary conditions in Equation \ref{eq:12.3.16} require products \(v(x,y)=X(x)Y(y)\) such that \(Y(0)=Y'(b)=X'(a)=0\); hence, we let \(k=\lambda\) in Equation \ref{eq:12.3.3}. Thus, \(X\) and \(Y\) must satisfy
\[\label{eq:12.3.17} X''-\lambda X=0,\quad \quad X'(a)=0\]
and
\[\label{eq:12.3.18} Y''+\lambda Y=0,\quad Y(0)=0,\quad Y'(b)=0.\]
From Theorem 11.1.4, the eigenvalues of Equation \ref{eq:12.3.18} are \(\lambda_n=(2n-1)^2\pi^2/4b^2\), with associated eigenfunctions
\[Y_n=\sin{(2n-1)\pi y\over2b}, \quad n=1,2,3,\dots.\nonumber\]
Substituting \(\lambda=(2n-1)^2\pi^2/4b^2\) into Equation \ref{eq:12.3.17} yields
\[X''-((2n-1)^2\pi^2/4b^2)X=0,\quad X'(a)=0,\nonumber\]
so we could take
\[\label{eq:12.3.19} X_n=\cosh{(2n-1)\pi(x-a)\over 2b}.\]
However, because of the nonhomogeneous Dirichlet condition at \(x=0\), it is better to require that \(X_n(0)=1\), which can be achieved by dividing the right side of Equation \ref{eq:12.3.19} by its value at \(x=0\); thus,
\[X_n= {\cosh(2n-1)\pi(x-a)/2b\over\cosh(2n-1)\pi a/2b}.\nonumber\]
Then
\[v_n(x,y)=X_n(x)Y_n(y)= {\cosh(2n-1)\pi(x-a)/2b\over\cosh(2n-1)\pi a/2b}\sin{(2n-1)\pi y\over2b},\nonumber\]
so
\[v_n(0,y)=\sin{(2n-1)\pi y\over2b}.\nonumber\]
Therefore \(v_n\) satisfies Equation \ref{eq:12.3.16} with \(g(y)=\sin(2n-1)\pi y/2b\). More generally, if \(\alpha_1\), …, \(\alpha_m\) are arbitrary constants then
\[u_m(x,y)=\sum_{n=1}^m \alpha_n {\cosh(2n-1)\pi(x-a)/2b\over\cosh(2n-1)\pi a/2b}\sin{(2n-1)\pi y\over 2b}\nonumber\]
satisfies Equation \ref{eq:12.3.16} with
\[g(y)=\sum_{n=1}^m \alpha_n\sin{(2n-1)\pi y\over2b}.\nonumber\]
Thus, if \(g\) is an arbitrary piecewise smooth function on \([0,b]\), we define the formal solution of Equation \ref{eq:12.3.16} to be
\[u(x,y)=\sum_{n=1}^\infty \alpha_n {\cosh(2n-1)\pi(x-a)/2b\over\cosh(2n-1)\pi a/2b}\sin{(2n-1)\pi y\over 2b},\nonumber\]
where
\[S_M(x)=\sum_{n=1}^\infty \alpha_n\sin{(2n-1)\pi y\over2b}\nonumber\]
is the mixed Fourier sine series of \(g\) on \([0,b]\); that is,
\[\alpha_n={2\over b}\int_0^bg(y)\sin{(2n-1)\pi y\over2b}\,dy.\nonumber\]
Solve Equation \ref{eq:12.3.16} with \(g(y)=y(2y^2-9by+12b^2)\).
Solution
From Example 11.3.8,
\[S_{M}(y)=\frac{96b^{3}}{\pi ^{3}}\sum_{n=1}^{\infty}\frac{1}{(2n-1)^{3}}\left[3+(-1)^{n}\frac{4}{(2n-1)\pi } \right]\sin\frac{(2n-1)\pi y}{2b}\nonumber \]
Therefore
\[u(x,y)=\frac{96b^{3}}{\pi ^{3}}\sum_{n=1}^{\infty }\frac{\cosh (2n-1)\pi (x-a)/2b}{(2n-1)^{3}\cosh (2n-1)\pi a/2b}\left [3+(-1)^{n}\frac{4}{(2n-1)\pi } \right]\sin\frac{(2n-1)\pi y}{2b}\nonumber\]
Define the formal solution of
\[\label{eq:12.3.20}\begin{array}{ccc}{u_{xx}+u_{yy}=0,}&{0<x<a,}&{0<y<b,}\\{u_{y}(x,0)=0,}&{u(x,b)=0,}&{0\leq x\leq a,}\\{u_{x}(0,y)=0,}&{u_{x}(a,y)=g(y),}&{0\leq y\leq b}\end{array}\]
(Figure 12.3.11 ).
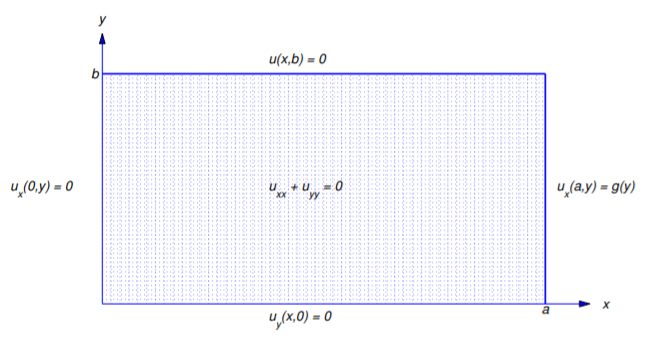
Solution:
The boundary conditions in Equation \ref{eq:12.3.20} require products \(v(x,y)=X(x)Y(y)\) such that \(Y'(0)=Y(b)=X'(0)=0\); hence, we let \(k=\lambda\) in Equation \ref{eq:12.3.3}. Thus, \(X\) and \(Y\) must satisfy
\[\label{eq:12.3.21} X''-\lambda X=0,\quad \quad X'(0)=0\]
and
\[\label{eq:12.3.22} Y''+\lambda Y=0,\quad Y'(0)=0,\quad Y(b)=0.\]
From Theorem 11.1.4, the eigenvalues of Equation \ref{eq:12.3.22} are \(\lambda_n=(2n-1)^2\pi^2/4b^2\), with associated eigenfunctions
\[Y_n=\cos{(2n-1)\pi y\over2b}, \quad n=1,2,3,\dots.\nonumber\]
Substituting \(\lambda=(2n-1)^2\pi^2/4b^2\) into Equation \ref{eq:12.3.21} yields
\[X''-((2n-1)^2\pi^2/4b^2)X=0,\quad X'(0)=0,\nonumber\]
so we could take
\[\label{eq:12.3.23} X_n=\cosh{(2n-1)\pi x\over 2b}.\]
However, because of the nonhomogeneous Neumann condition at \(x=a\), it is better to require that \(X_n'(a)=1\), which can be achieved by dividing the right side of Equation \ref{eq:12.3.23} by the value of its derivative at \(x=a\); thus,
\[X_n= {2b\cosh(2n-1)\pi x/2b\over(2n-1)\pi\sinh(2n-1)\pi a/2b}.\nonumber\]
Then
\[v_n(x,y)=X_n(x)Y_n(y)= {2b\cosh(2n-1)\pi x/2b\over(2n-1)\pi\sinh(2n-1)\pi a/2b}\cos{(2n-1)\pi y\over2b},\nonumber\]
so
\[{\partial v_n\over\partial x}(a,y)=\cos{(2n-1)\pi y\over2b}.\nonumber\]
Therefore \(v_n\) satisfies Equation \ref{eq:12.3.20} with \(g(y)=\cos(2n-1)\pi y/2b\). More generally, if \(\alpha_1\), …, \(\alpha_m\) are arbitrary constants then
\[u_m(x,y)={2b\over\pi}\sum_{n=1}^m \alpha_n {\cosh(2n-1)\pi x/2b\over(2n-1)\sinh(2n-1)\pi a/2b}\cos{(2n-1)\pi y\over 2b}\nonumber\]
satisfies Equation \ref{eq:12.3.20} with
\[g(y)=\sum_{n=1}^\infty \alpha_n\cos{(2n-1)\pi y\over2b}.\nonumber\]
Therefore, if \(g\) is an arbitrary piecewise smooth function on \([0,b]\), we define the formal solution of Equation \ref{eq:12.3.20} to be
\[u(x,y)={2b\over\pi}\sum_{n=1}^\infty \alpha_n {\cosh(2n-1)\pi x/2b\over(2n-1)\sinh(2n-1)\pi a/2b}\cos{(2n-1)\pi y\over 2b},\nonumber\]
where
\[C_M(y)=\sum_{n=1}^\infty \alpha_n\cos{(2n-1)\pi y\over2b}\nonumber\]
is the mixed Fourier cosine series of \(g\) on \([0,b]\); that is,
\[\alpha_n={2\over b}\int_0^bg(y)\cos{(2n-1)\pi y\over2b}\,dy.\nonumber\]
Solve Equation \ref{eq:12.3.20} with \(g(y)=y-b\).
Solution
From Example 11.3.3,
\[C_M(y)=-{8b\over\pi^2}\sum_{n=1}^\infty{1\over(2n-1)^2} \cos{(2n-1)\pi y\over2b}. \nonumber\]
Therefore
\[u(x,y)=-{16b^2\over\pi^3}\sum_{n=1}^\infty{ \cosh(2n-1)\pi x/2b\over(2n-1)^3\sinh(2n-1)\pi a/2b} \cos{(2n-1)\pi y\over2b}.\nonumber\]
Laplace's Equation for a Semi-Infinite Strip
We now seek solutions of Laplace’s equation on the semi-infinite strip
\[S:\{ 0<x<a,\quad y>0\} \nonumber\]
(Figure 12.3.12 ) that satisfy homogeneous boundary conditions at \(x=0\) and \(x=a\), and a nonhomogeneous Dirichlet or Neumann condition at \(y=0\). An example of such a problem is
\[\label{eq:12.3.24} \begin{array}{c} {u_{xx}+u_{yy}=0,\quad 0<x<a,\quad y>0,}\\{u(x,0)=f(x),\quad 0\leq x\leq a,}\\{u(0,y)=0,\quad u(a,y)=0,\quad y>0,}\end{array}\]
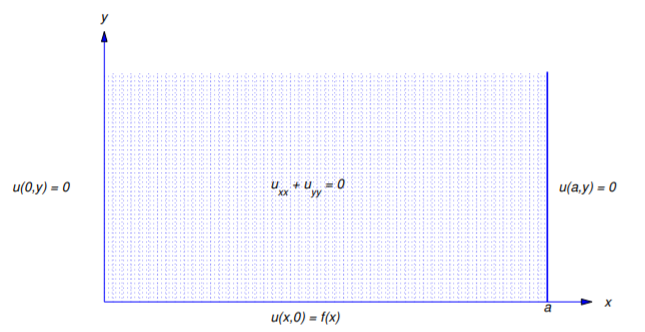
The boundary conditions in this problem are not sufficient to determine \(u\), for if \(u_0=u_0(x,y)\) is a solution and \(K\) is a constant then
\[u_1(x,y)=u_0(x,y)+K\sin{\pi x\over a}\sinh{\pi y\over a}.\nonumber\]
is also a solution. (Verify.) However, if we also require — on physical grounds — that the solution remain bounded for all \((x,y)\) in \(S\) then \(K=0\) and this difficulty is eliminated.
Define the bounded formal solution of Equation \ref{eq:12.3.24}.
Solution
Proceeding as in the solution of Example 12.3.1 , we find that the building block functions are of the form
\[v_n(x,y)=Y_n(y)\sin{n\pi x\over a}, \nonumber\]
where
\[Y_n''-(n^2\pi^2/a^2)Y_n=0. \nonumber\]
Therefore
\[Y_n=c_1e^{n\pi y/a}+c_2e^{-n\pi y/a} \nonumber\]
where \(c_1\) and \(c_2\) are constants. Although the boundary conditions in Equation \ref{eq:12.3.24} don’t restrict \(c_1\), and \(c_2\), we must set \(c_1=0\) to ensure that \(Y_n\) is bounded. Letting \(c_2=1\) yields
\[v_n(x,y)=e^{-n\pi y/a}\sin{n\pi x\over a}, \nonumber\]
and we define the bounded formal solution of Equation \ref{eq:12.3.24} to be
\[u(x,y)=\sum_{n=1}^\infty b_ne^{-n\pi y/a}\sin{n\pi x\over a}, \nonumber\]
where
\[S(x)=\sum_{n=1}^\infty b_n\sin{n\pi x\over a} \nonumber\]
is the Fourier sine series of \(f\) on \([0,a]\).
See Exercises 12.3.29-12.3.34 for other boundary value problems on a semi-infinite strip.


